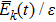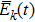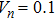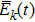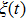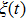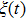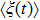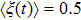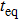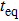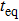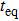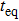† Corresponding author. E-mail:
We study the dynamical energy equipartition properties in the integrable Toda model with additional uniform or disordered on-site energies by extensive numerical simulations. The total energy is initially equidistributed among some of the lowest frequency linear modes. For the Toda model with uniform on-site potentials, the energy spectrum keeps its profile nearly unchanged in a relatively short time scale. On a much longer time scale, the energies of tail modes increase slowly with time. Energy equipartition is far away from being attached in our studied time scale. For the Toda model with disordered on-site potentials, the energy transfers continuously to the high frequency modes and eventually towards energy equipartition. We further perform a systematic study of the equipartition time teq depending on the energy density ε and the nonlinear parameter α in the thermodynamic limit for the Toda model with disordered on-site potentials. We find 
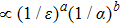
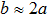
Since the pioneering work of Fermi, Pasta and Ulam (FPU)[1] revealed that recurrence of the energy on the initial excited modes prevented energy equipartition in the FPU model, there have been large activities for many years in the study of the temporal evolution of an initially localized energy excitation in various nonlinear systems.[2–27] For the FPU-α model, two stage dynamics are found at weak nonlinearity.[23] At the first stage of the dynamics, the energies of the unexcited modes grow with time for a certain time scale. After that, the energy spectrum keeps its profile nearly unchanged. At the second stage of the dynamics, the energies of tail modes increase and eventually move towards energy equipartition. Further studies find that the equipartition time 
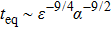
The question we focus on in this paper is whether the effect of on-site potentials may cause the dynamical energy equipartition of the integrable Toda model. Therefore, we investigate the energy transport properties of the integrable Toda model with additional uniform or disordered on-site potentials. We organize the paper as follows. The model, and the method of numerical experiments are introduced in Section
The Hamiltonian we discuss here is
 |
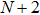
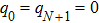
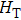
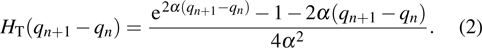 |
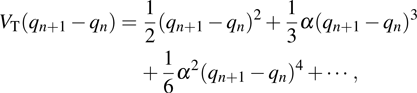 |
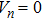
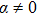
In the linear case (α = 0), equation (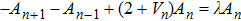
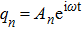
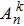
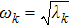
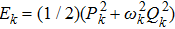
We define the time averaged energy spectrum 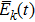
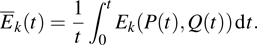 |

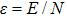
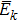
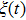
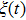
 |
The definition of 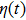
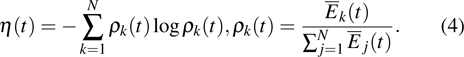 |
At first, some of the lowest frequency normal modes are excited, with identical energy. The Hamilton equation of motion is solved numerically with the help of the 
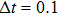
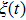
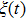
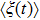

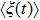
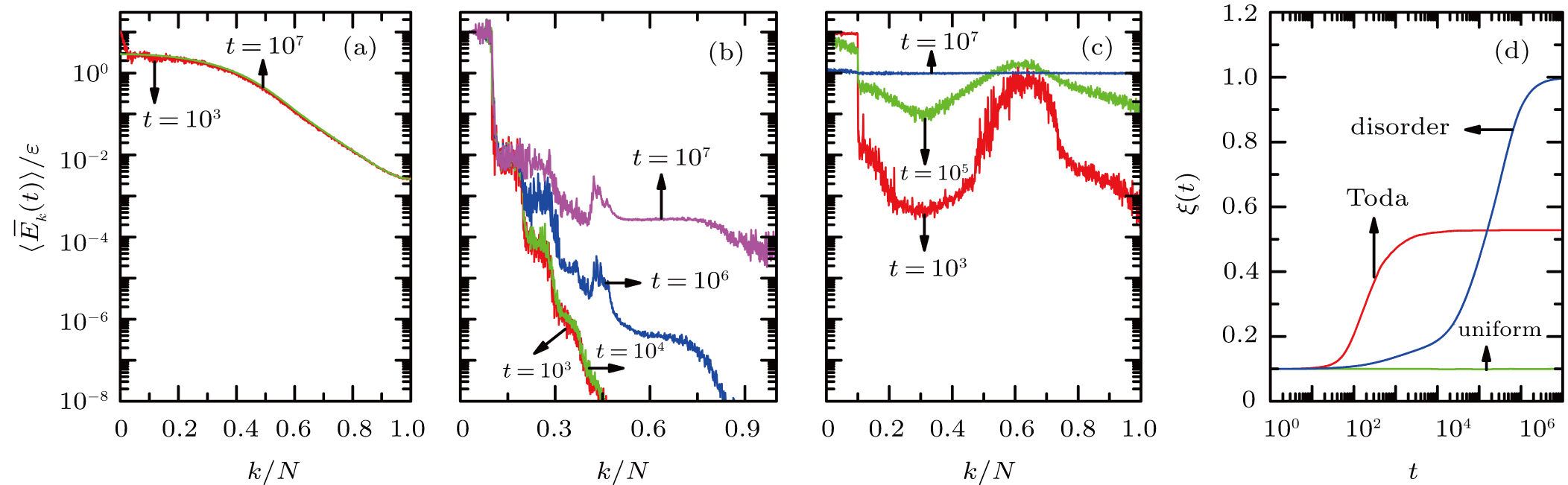
The results of the time averaged energy spectrum 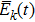

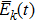
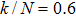
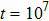
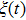
One can see from Fig. 
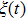
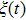
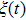
Figure 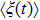
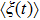


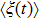
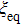
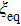
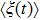
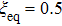

In the following, we turn to clarify the equipartition time 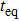
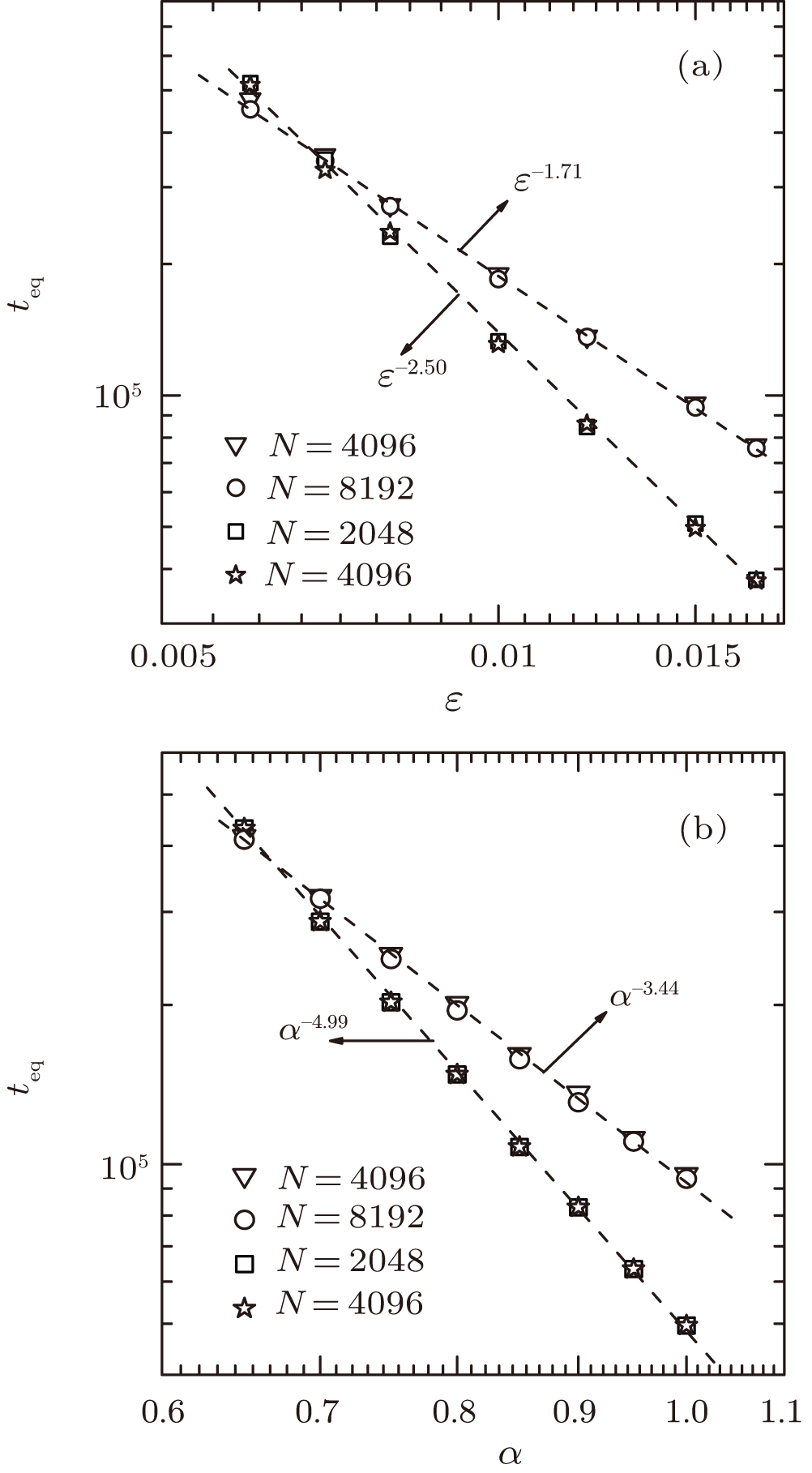
Firstly, we study the dependence of 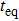
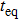
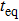
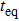
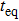

 | Fig. 3. The dependencies of  |
Secondly, we study the dependence of 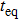
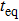
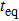

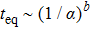
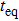
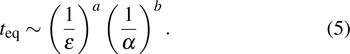 |
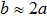
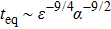
Thirdly, we study the values of a and b depending on the strengths of disordered on-site potentials. Figure 
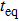
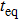
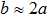
Finally, we study the values of a and b depending on different initial conditions in the thermodynamics limit. The results of 

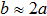
In summary, we studied the energy equipartition properties in the integrable Toda model with additional uniform or disordered on-site energies by extensive numerical simulations. Some of the lowest frequency normal modes are initially excited, with identical energy. Due to the integrable property of the Toda model, the energy of high frequency modes remains very small and does not grow with time. The energy equipartition state is sure to not be attached. However, the energy transport behavior becomes very different for the Toda model with uniform or disordered on-site energies. For the Toda model with uniform on-site energies, the energy spectrum keeps its profile nearly unchanged for a certain time scale. After that, the energies of tail modes increase with time. The process of energy transfer to high frequency modes is very slow and energy equipartition is far away from being attached in our studied time scale. For the Toda model with disordered on-site energies, the energy of the high frequency modes grows continuously with time and eventually towards energy equipartition. Therefore, the integrable property of the Toda model is destroyed and the energy transfers to the high frequency modes with uniform or disordered on-site energies. Moreover, the process of energy transport is much faster for the Toda model with disordered on-site energies than that with uniform on-site energies. We further studied the equipartition time 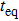
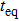
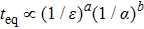
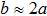
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] |