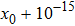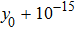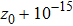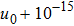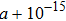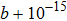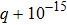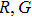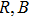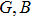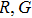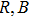Cite this Article
Zhang Li-Min, Sun Ke-Hui, Liu Wen-Hao, He Shao-Bo. A novel color image encryption scheme using fractional-order hyperchaotic system and DNA sequence operations. Chinese Physics B, 2017, 26(10): 100504  
Permissions
A novel color image encryption scheme using fractional-order hyperchaotic system and DNA sequence operations
Zhang Li-Min, Sun Ke-Hui †, Liu Wen-Hao, He Shao-Bo
School of Physics and Electronics, Central South University, Changsha 410083, China

 

† Corresponding author. E-mail: kehui@csu.edu.cn

Abstract

In this paper, Adomian decomposition method (ADM) with high accuracy and fast convergence is introduced to solve the fractional-order piecewise-linear (PWL) hyperchaotic system. Based on the obtained hyperchaotic sequences, a novel color image encryption algorithm is proposed by employing a hybrid model of bidirectional circular permutation and DNA masking. In this scheme, the pixel positions of image are scrambled by circular permutation, and the pixel values are substituted by DNA sequence operations. In the DNA sequence operations, addition and substraction operations are performed according to traditional addition and subtraction in the binary, and two rounds of addition rules are used to encrypt the pixel values. The simulation results and security analysis show that the hyperchaotic map is suitable for image encryption, and the proposed encryption algorithm has good encryption effect and strong key sensitivity. It can resist brute-force attack, statistical attack, differential attack, known-plaintext, and chosen-plaintext attacks.

PACS: 05.45.-a;05.45.Vx;05.45.Gg
Keyword:color image encryption;DNA sequence operation;fractional calculus;piecewise-linear hyperchaotic system
1. Introduction

Based on network and cloud computing, the development of the information technology brings lots of challenges to protection of confidential and sensitive transmitted information, and the information security of digital information has become a hot topic.[1–7] The encryption is very important for the image transmission, such as military image and private image.[8,9] However, most conventional ciphers such as Data Encryption Standard (DES) and International Data Encryption Algorithm (IDEA) are not suitable for digital images, because of the inherent features of image data including the bulk data capacity and strong correlation among adjacent pixels. Due to the advantages in extreme sensitivity to initial conditions and parameters, ergodicity, high randomness and mixing, the chaotic signals possess great value in the field of cryptography, and a lot of chaos-based cryptosystems have been developed up to now.[4–9]

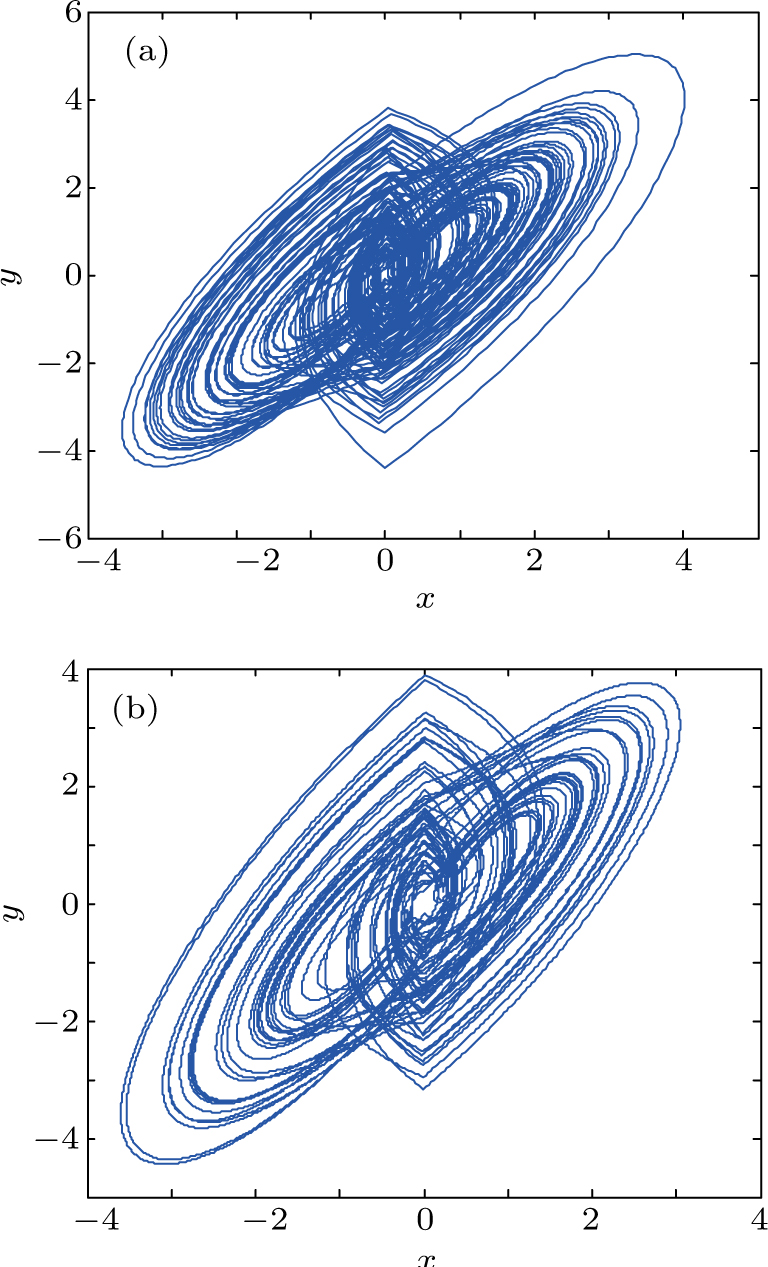
Compared with integer-order chaotic system, the encryption scheme based on fractional-order system has higher security because of its nonlocal character and high nonlinearity.[10,11] In addition, the key space is greatly improved by introducing fractional-order system, although its computing cost maybe increase. For the sake of security improvement, on one hand, the novel piecewise-linear (PWL) hyperchaotic system[12] is solved by ADM algorithm,[13–15] which owns less time and more space complexity. The system possesses seven terms without any quadratic or higher-order polynomials, and contains the piecewise continuous functions, such as absolute value function. Thus, it is meaningful to study the system dynamics and its applications in the image encryption. On the other hand, we reduce the iteration cost of hyperchaotic system in the encryption algorithm as far as possible.

Many hybird algorithms have been proposed[16–29] to improve the security. Among them, DNA-based algorithm arises most of concerned,[18–22,24,28] because DNA computing has some good characteristics such as massive parallelism, huge storage and ultra-low power consumption. The core of these schemes are DNA encoding and DNA computing, which includes some biological and algebra operations on DNA sequence, such as the DNA complementary rule,[20] DNA addition[21,22,28] and XOR operations.[24] However, most of these algorithms cannot resist differencial attack, because their ciphered image only relys on the secret key. Attackers may use some special plaintext image to crack these schemes. To address this problem, we proposed a scheme that the ciphered image not only depends on the secret key, but also relys on the plaintext. It improves the ability to resist these attacks greatly.

In this paper, based on the fractional-order PWL hyperchaotic map, we proposed a new image encryption scheme. In this scheme, permutation and substitution are combined to smash the correlations between R, G, B components, and design a rule of twin DNA addition for DNA operation. The rest of this paper is organized as follows. In Section 2, several different definitions of fractional calculus are presented as the preliminary. In Section 3, the fractional-order hyperchaotic map is obtained by ADM algorithm, and DNA rules is introduced. The encryption and decryption scheme is described in Section 4. Security analysis is given in Section 5. Finally, we summarize the results.

2. Basic definition and preliminary

There are several different definitions of fractional-order integration and differential so far,[10,11] such as Riemann-Liouville definition and Caputo definition.

Definition 1 The Riemann–Liouville fractional-order derivative of function with order q is defined as

where is the Gamma function, , .

Definition 2 The Caputo fractional-order derivative of function with order q is defined by

where is the Gamma function, and . is the m-th order derivative, such that , .

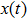
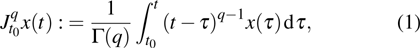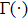
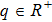
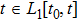
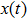
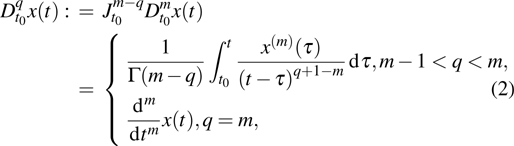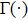
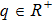
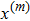
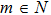
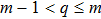
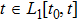
Although the Riemann–Liouville derivative and Caputo derivative are equivalent in the same homogenous initial conditions, the Caputo derivative (2) ensures a direct connection between the kinds of the initial condition and the fractional-order derivative.[12] Grounded on these considerations, the Caputo derivative is employed in ADM decomposition algorithm. So the solution of the system (1) is expressed as

where
is the initial value. is the Adomian polynomial, and is constant for autonomous system. is derived from

3. Fractional-order hyperchaotic system and DNA rules
3.1. Fractional-order piecewise-linear hyperchaotic map

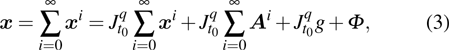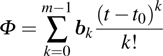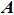
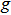
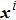
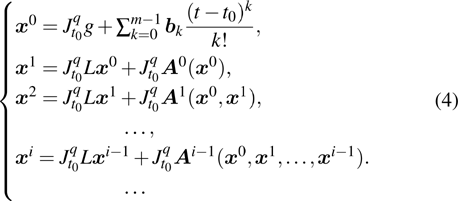The equation of integer-order PWL hyperchaotic system proposed by Li et al.,[12] and its fractional-order form is expressed as

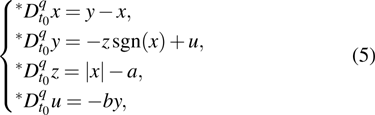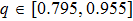
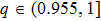
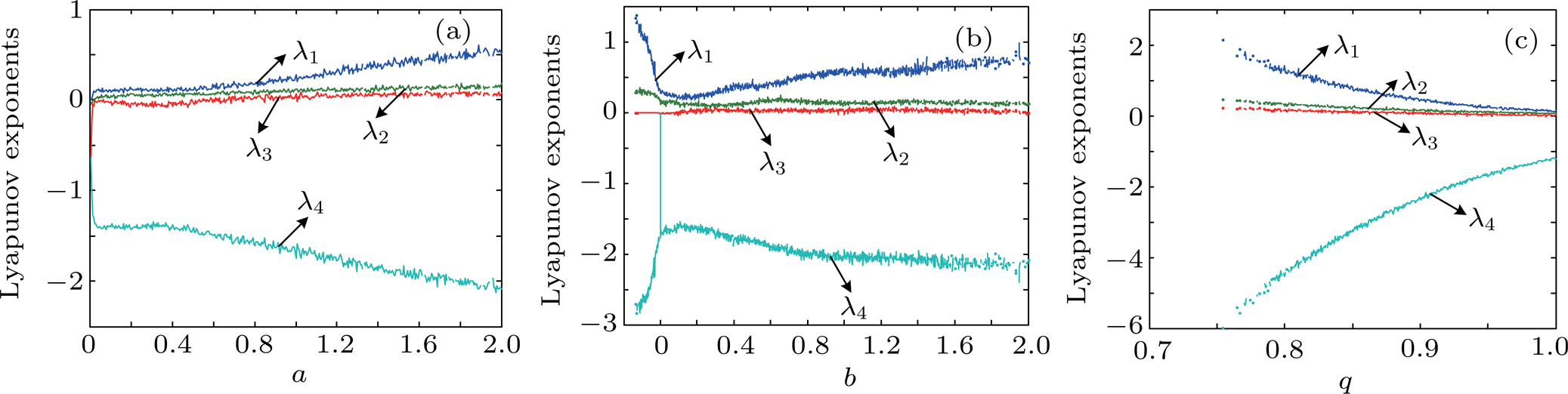where a and b are the system parameters. The dynamical equations have seven terms without any quadratic or higher-order polynomials, so it also reduces the computational complexity. To our knowledge, it is the simplest hyperchaotic system, which possesses complex dynamics. Equation (5) is solved by applying the ADM algorithm.[13,15] The Lyapunov exponents are shown in Fig. 1. When we fix a = 1, q = 0.95, and b is variable in the range [−0.138, 2], the system generates hyperchaos. When we fix b = 0.25, q = 0.95, the system is chaotic for , and it generates hyperchaos for . When we fix and b = 0.25, the system is hyperchaotic for , and it generates chaos for . The chaotic attractors are shown in Fig. 2 with a = 1, b = 0.25 and q = 0.75 or q = 1 respectively.

Fig. 1. (color online) The Lyapunov exponents of the PWL fractional-order system (a) q = 0.95, b = 0.25, 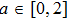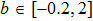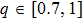; (b) a = 1, q = 0.95, ; (c) a = 1, b = 0.25, .
Fig. 2. (color online) Strange attractors for the PWL fractional-order system while fixing a = 1, b = 0.25; (a) q = 0.75; (b) q = 1.
3.2. DNA encoding and decoding rules

A DNA sequence consists of four nucleic acid bases A (adenine), G (guanine), T (thymine), C (cytosine), where T and A are complementary, and C and G are complementary. For a binary signal, 0 and 1 are complementary, so it is obtained that 00 and 11 are complementary, and 01 and 10 are also complementary. By using the four bases A, C, G, and T to encode 00, 01, 10, and 11, the number of coding combination kinds is 4! = 24. Because of the complementary relationamong DNA bases, there are only eight kinds of coding combinations which satisfy the Watson–Crick complement rule[25] as listed in Table 1. DNA decoding is the inverse of DNA encoding. For example, if the first pixel value of the red channel image is 216, it is converted into a binary sequence as [11011000]. By using the DNA encoding Rule 1 to encode it, we obtain the DNA sequence [TCGA]. If the encoded sequence is [TGCA], it is decoded to [00100111] according to Rule 2, and the decimal value is 39 for the DNA decoding result.

Table 1.

DNA encoding rules.

.
3.3. The addition and subtraction operations for DNA sequence

For DNA sequences, addition and subtraction operations are performed according to traditional addition and subtraction in the binary. Thus, there are 8 kinds of DNA addition and subtraction rules corresponding to 8 kinds of DNA encoding schemes. For instance, we adopt one type of addition operation as shown in Table 2 to add [AGCT] and [CTGA], and a sequence [CCTT] is obtained. Similarly, we obtain the sequence [ACCT] by subtracting the sequence [CTGA] from [CATT]. The subtraction operation is shown in Table 3.

Table 2.

Addition operation for DNA sequences.

.
Table 3.

Subtraction operation for DNA sequences.

.
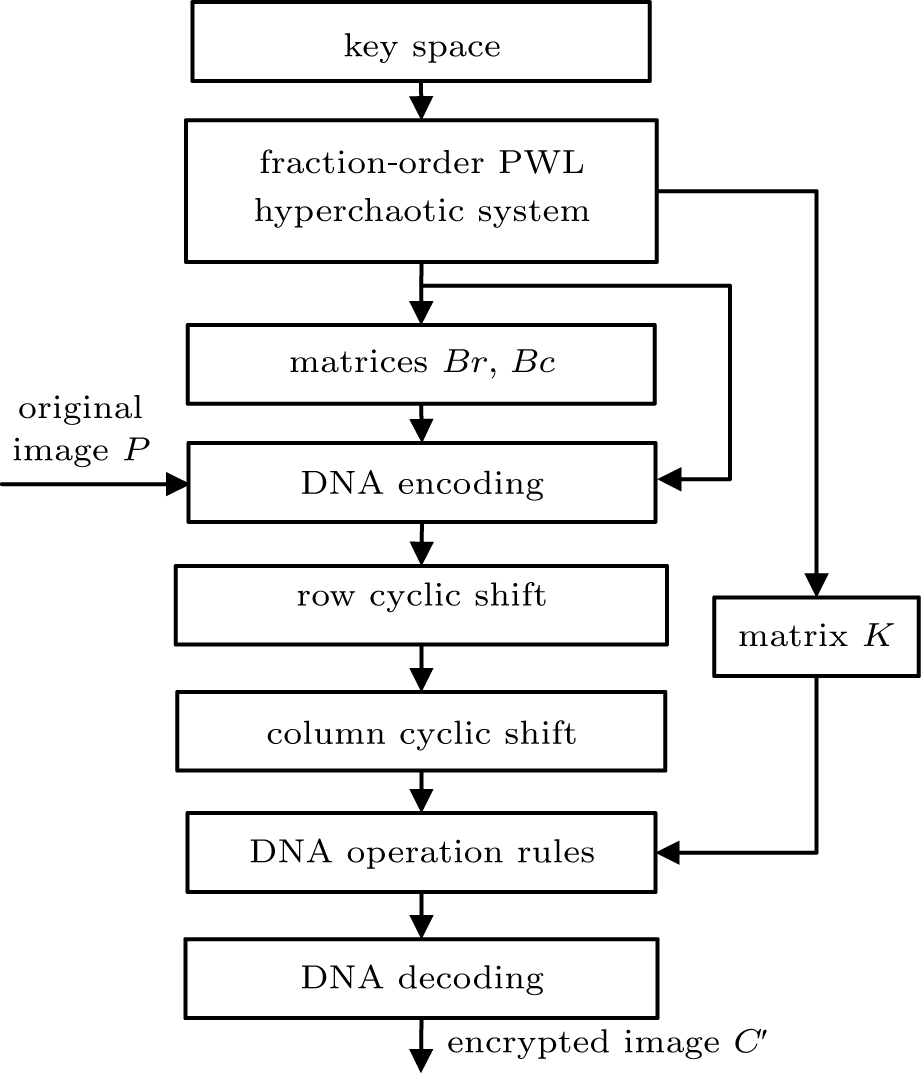
4. Image encryption and decryption scheme
4.1. Key format

The key format used in this encryption scheme is shown in Fig. 3. It is consisted of twelve components, including parameters a and b of system (5), the system order q, the initial conditions , , , and , pre-iteration numbers m and n, initial nucleic acid base (), indexes of DNA encoding rules in Table 1 α and β ().

Fig. 3. Key format.
4.2. Image encryption and decryption

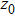
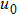
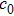
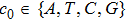
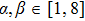
The flowchart of encryption scheme is shown in Fig. 4. As can be seen, the fractional-order PWL hyperchaotic map is used as pseudo-random generator. The pixel positions are scrambled by circular permutation, and there are two directions (up, left) to shift. The pixel values are substituted by using DNA addition rule. The specific algorithm can be divided into circular permutation in both directions and DNA sequence operations stages as follows.

Fig. 4. Flowchart of the proposed encryption scheme.

Step 1 Generation of initial conditions. Assign a, b, q, , , , with the corresponding value in key. Inputting the original image P with the size of , initial conditions of system (3) are generated by

Step 2 Generation of pseudo-random sequence. Set , and the system (3) is iterated for times and discard the former m values to avoid the transient effect and enhance initial value sensitivity. Then hyperchaotic sequences , , , and are obtained to calculate shift step numbers as follows.

where is the step numbers of circular shift in row i, and is the step numbers of circular shift in column j, where, and .

Step 3 Decomposing the RGB image P into , , components, and then transform , , and to binary matrices R, G, and B with the size of and combine them into a matrix. Then the matrix is encoded by using the DNA encoding rule α, and the DNA sequence matrix T is obtained.

Step 4 Rows circular shift. The rows shift result is obtained by following rules. The row i of is moved to left with step numbers ; .

Step 5 Columns circular shift. The columns shift S is obtained by following rules. The column j of is moved to up with step numbers ; .

Step 6 Generation of encoded key sequence. The obtained hyperchaotic sequences , , , in the Step 2 are combined into one sequence P by

where . Then the new pseudo-random sequence k is obtained by

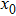
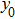
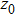
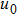
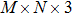
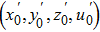
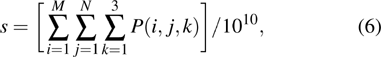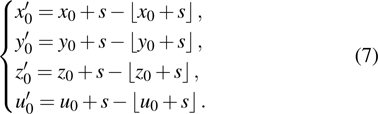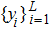
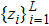
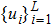
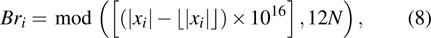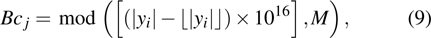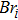
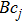
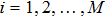
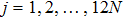
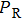
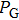
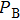
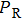
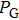
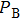
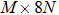
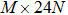
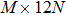
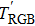
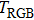
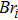
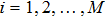
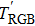
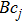
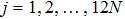
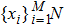
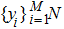
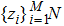
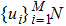
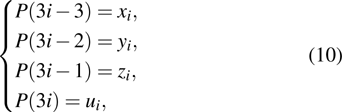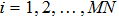
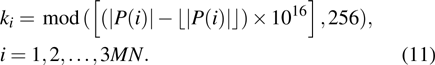The sequence k is transformed to binary matrix, and the matrix is encoded by using the same DNA rule α to obtain the matrix K with .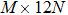

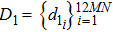
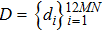
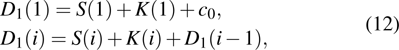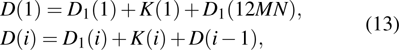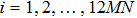
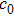
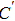
Step 7 DNA operation rules. According to the value of known ciphertext, two rounds of addition rules are employed to encrypt the pixel values. So it does not need a lot of iterations of chaotic system, and has good substitution effect. After the two rounds of addition, the final encrypted image of DNA formulation matrixs and are calculated by

where , and “+” is the DNA addition operation. is one of the keys.

Step 8 DNA decoding. The matrix D is decoded by using the DNA rule β and then recover RGB image to obtain encrypted image .

Remark 1 The advantage of this permutation algorithm is that a pixel may be permuted to any position of the image due to the combined operations of R, G, B components.

Remark 2 The number s obtained in the Step 1 is used in the decryption algorithm.

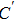
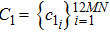
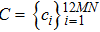
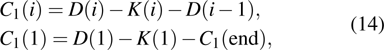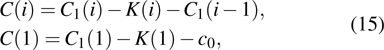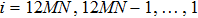
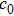
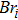
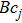
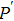
The decryption algorithm is the inverse of encryption algorithm. First of all, the encrypted image is encoded as matrix D using DNA Rule β, and the middle decryption result of DNA formulation matrix and is recovered by

where , and “−” is the DNA subtraction operation. is one part of keys. The key matrix K is generated by doing step 6 of DNA operations. The number s is obtained in the Step 1 of encryption algorithm must be used here. Secondly, by using the number s above, we carry out the same iteration as Step 1 to generate the step numbers and . Finally, the decrypted image is recovered by circular shift of matrix S, and it is worth noting that the direction of shift is opposite to the encryption process.

4.3. Simulation results

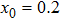
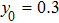
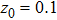
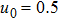
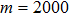
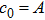
The simulation experiments are carried out on MATLAB 8.1, and the results are shown in Fig. 5. The color Lena image is used as the plaintext as shown in Fig. 5(a) with the size of 256 × 256. The key is set as a = 1, b = 0.25, q = 0.75, , , , , , n = 2000, , α = 1, β = 1. The encrypted Lena image is shown in Fig. 5(b), and the corresponding decrypted image is shown in Fig. 5(c).

Fig. 5. (color online) Encryption and decryption results (a) original Lena image; (b) encrypted Lena image; (c) decrypted Lena image.
5. Security analysis
5.1. Key space

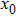
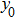
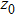
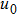
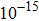
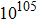
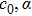
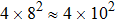
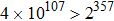
The size of the key space is the total number of different keys that should be large enough to withstand the brute-force attack. For the keys , , , , a, b, and q, if the calculation precision is , the key space will be . For the keys and β, because there are four nucleic acid bases and eight DNA encoding and decoding rules, the key space is . So the total key space is about , which is large enough to resist the brute-force attack.

5.2. Key sensitivity analysis

An efficient encryption scheme should also be sensitive to its secret key. It means that a very small change in the key will cause a significant change in the decrypted image. In this test, we employ a scheme to slightly change the keys to the following

and α + 1 to decrypt the encrypted Lena image as shown in Fig. 5(b), and the results are shown in Fig. 6. Obviously, these decrypted images are different from the correctly decrypted image as shown in Fig. 5(c). Therefore, the proposed algorithm is extremely sensitive to its keys.

Fig. 6. (color online) The results of key sensitivity test (a) decryption with ; (b) decryption with ; (c) decryption with ; (d) decryption with ; (e) decryption with ; (f) decryption with ; (g) decryption with ; (h) decryption with α + 1.
5.3. Statistical analysis

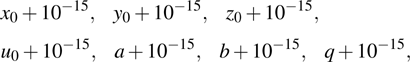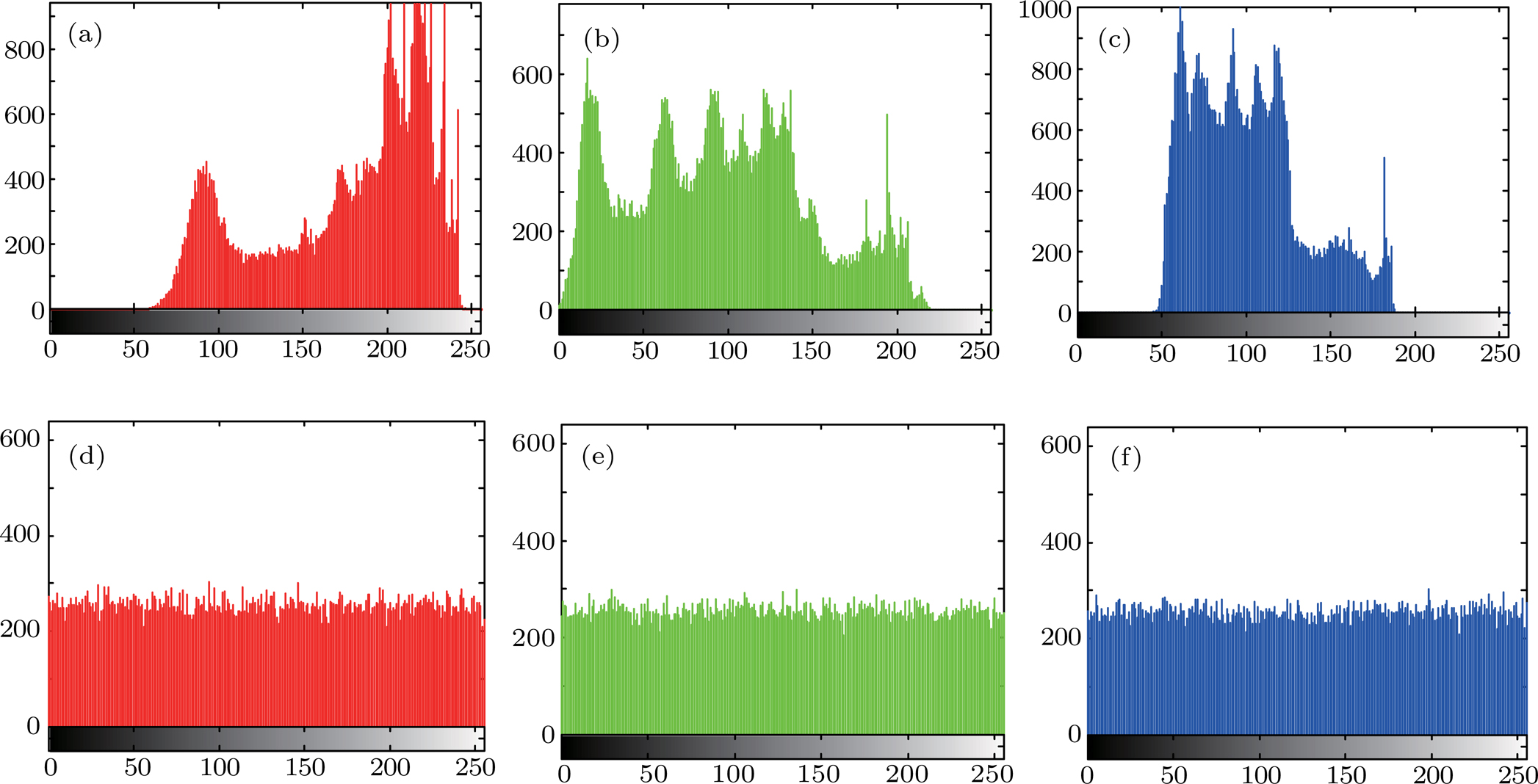
Shannon suggested that diffusion and confusion should be employed in a cryptosystem for frustrating a powerful statistical analysis.[26] Histogram and correlation coefficient of two adjacent pixels are employed to assess the ability of resisting statistical attack.

1) Histogram analysis

An ideal encryption algorithm should be robust against any statistical attack. Figure 7 displays the histograms of the original image and its encrypted image. From these figures, it is obvious that the histograms of the encrypted image are uniform and significantly different from those of the original image.

Fig. 7. (color online) Histograms of the original Lena image and its encrypted image. (a) Original image in R channel; (b) original image in G channel; (c) original image in B channel; (d) encrypted image in R channel; (e) encrypted image in G channel; (f) encrypted image in B channel.

2) Correlation coefficient analysis

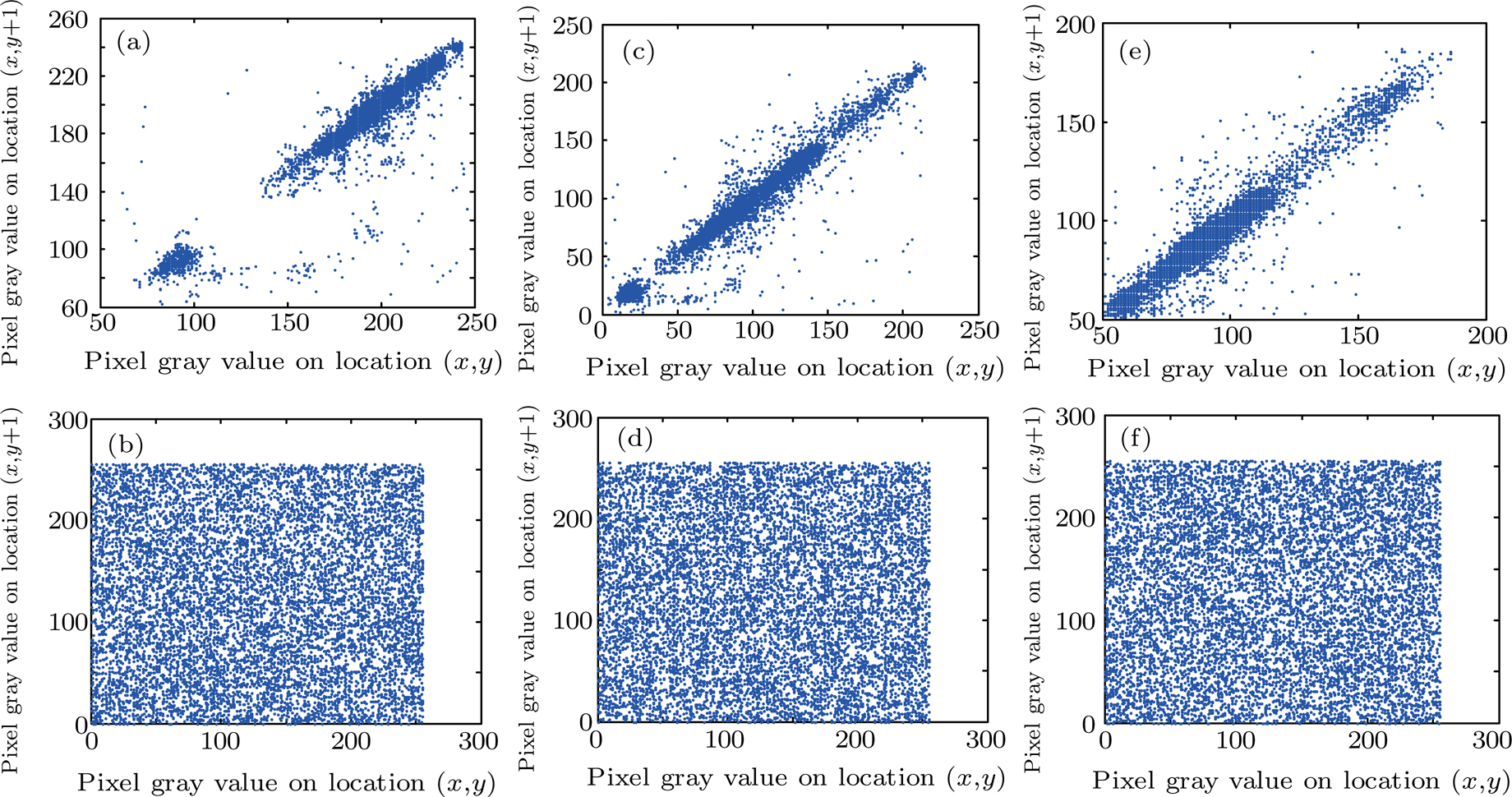
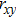
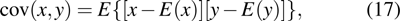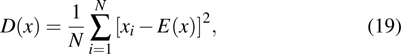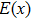
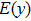
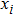
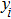
The effectiveness of an encryption algorithm is measured by the correlation of images. The correlation coefficient between two adjacent pixels x and y is defined by the following expressions

where N is the total number of pixels, and and are the means of and , respectively. The results of correlation coefficients for two horizontally, vertically, and diagonally adjacent pixels in R, G, and B channels of the original Lena image and its encrypted image are listed in the Table 4, Table 5, and Table 6, respectively. The results indicate that the correlations of the original images are high, while the correlations of the encrypted images are very low. Compared the results with other references, it is shown that the encryption effect is satisfactory.

Table 4.

Correlation coefficients of the original and encrypted images in R, G, B channels.

.
Table 5.

Identical position correlation coefficients among R, G, and B channels.

.
Table 6.

Adjacent position correlation coefficients among R, G, and B channels.

.

To demonstrate this result clearly, figure 8 represents the correlation distributions of diagonally adjacent pixels for Lena image. As shown in Figs. 8(a),8(c),8(e), there is strong correlation between adjacent pixels of original image because all the dots are congregated along the diagonal. Relatively, the dots are scattered over the entire plane as shown in Figs. 8(b),8(d), and 8(f). It indicates that the correlation is greatly reduced in the encrypted image.

Fig. 8. (color online) Correlation distributions between two diagonal adjacent pixels: (a) original image in R channel; (b) encrypted image in R channel; (c) original image in G channel; (d) encrypted image in G channel; (e) original image in B channel; (f) encrypted image in B channel.
5.4. Information entropy

The randomness of gray value is evaluated by information entropy, and it is defined by

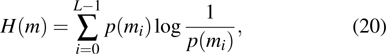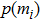
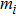
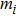
where is the probability of symbol , and L is the total number of symbols . For a 256-gray-level image, the ideal value of information entropy is 8. The information entropy of encrypted images in R, G, B channels and the combination of R, G, B components S is shown in Table 7. It is clear that the experimental values of our algorithm are close to 8 extremely. Thus, the encrypted images possess good randomness.

Table 7.

Information entropy of encrypted images.

.
5.5. Differential attack

For an encryption algorithm, the ability of resisting differential attack is connected with the sensitivity to original image. It is evaluated by the number of pixels change rate (NPCR) and unified average changing intensity (UACI). The formula of calculating NPCR and UACI are defined as

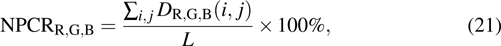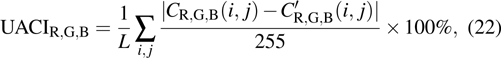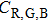
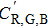
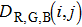
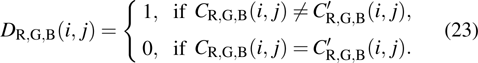where L is the number of pixels in the image. and are respectively encrypted images before and after one pixel of the original image is changed, and is calculated by

In our experiments, we only change the lowest bit of one random pixel of the original image. The average NPCRs and UACIs are obtained as listed in Table 8 after carrying out the test for 15 times. The data shows that the mean NPCRs and UACIs of the proposed algorithm are over 99.6% and 33.3%, respectively. The results show that the proposed algorithm could resist plaintext attack and differential attack effectively.

Table 8.

Mean NPCRs and UACIs of encrypted images.

.
5.6. Time complexity analysis

We test the efficiency of this encryption algorithm. The experimental environment is MATLAB R2012a with Intel(R) Core(TM) i3-2350M CPU @ 2.3 GHz and 6.0G RAM on Windows 8 OS. In this experiment, the 256 × 256 color Lena image is encrypted by one round of each algorithm, and the total execution time is 3.4095 s, including 2.5805-s iteration time of fractional-order hyperchaotic system. The convergence rate of the ADM algorithm is faster than others, such as Adams–Bashforth–Moulton (ABM) algorithm and frequency-domain method. Although it is relative slow compared with the algorithm of integer-order chaotic system, ADM algorithm also has excellent convergence speed and accuracy.[30] In addition, if the experiment is implemented on other platform like C/C++, the speed will be faster.

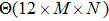
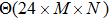
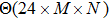
In the key generation of permutation process, the proposed algorithm has low execution time because it only needs iterations of fractional-order hyperchaotic system. The obtained hyperchaotic sequences will be saved and used in the DNA encoding and decoding key generation. Thus, the encryption time is shortened twice more by using the same sequences. In the DNA encoding and decoding process, the computation time of our algorithm needs iterations. In the diffusion process, the time-consuming parts are the operation of multiplying floating point numbers and DNA computing. The proposed algorithm needs iterations of two rounds of DNA addition. Therefore, the total time complexity for our proposed algorithm is .

6. Conclusion

In this paper, based on the fractional-order PWL hyperchaotic map, a novel color image encryption algorithm is proposed combining with DNA sequence operations. The pixel values of the original image are shuffled by DNA sequence addition operation with the key matrix, and the positions of pixels are permuted by the pseudorandom sequences generated from the fractional-order PWL hyperchaotic systems in bidirectional directions. The experiments and security tests show the novel scheme has good encryption effect. It possesses large key space and high sensitive to the key, and can resist common attacks, such as statistical, differential, brute-force, known-plaintext, and chosen-plaintext attacks. Thus, the proposed algorithm has wide application prospect in the future.

Reference
[1] Li J H Liu H 2013 IET Inform. Secur. 7 265
[2] Li C Q 2016 Signal Process 118 203
[3] Ai X X Sun K H He S B et al. 2014 Acta Phys. Sin. 63 120511 in Chinese
[4] Zhang W Yu H Zhu Z L 2015 Opt. Commun. 338 199
[5] Liu W H Sun K H Zhu C X 2016 Opt. Laser. Eng. 84 26
[6] Ye G D Zhao H Q Chai H J 2016 Nonlinear Dyn. 83 2067
[7] Chai X L Gan Z H Lu Y Zhang M H Chen Y R 2016 Chin. Phys. 25 100503
[8] Gong L H Liu X B Zheng F Zhou N R J. Mod. Opt. 60 1074
[9] Liu Z J Li S Liu W Liu S T Opt. Laser. Eng. 51 224
[10] Oldham K B Spanier J 1974 The Fractional Calculus: Theory and Application of Differentiation and Integration to Arbitrary Order New York Academic Press 46 10.1007/978-3-642-18101-6_2
[11] Bhalekar S 2012 Signal Image Video Process 6 513
[12] Li C B Sprott J C Thio W et al. 2014 IEEE Trans. Circuits Syst. II 61 977
[13] He S B Sun K H Wang H H 2015 Entropy 17 8299
[14] Momani S Al-Khaled K 2005 Appl. Math. Comput. 162 1351
[15] Wang H H Sun K H He S B 2015 Phys. Scr. 90 015206
[16] Adleman L 1994 Science 266 1021
[17] Chai X L Gan Z H Lu Y et al. 2016 Chin. Phys. 25 100503
[18] Zhang Q Guo L Wei X P 2010 Math. Comput. Model 52 2028
[19] Kumar M Iqbal A Kumar P 2012 Signal Process 125 187
[20] Liu H J Wang X Y Kadir A 2012 Appl. Soft Comput. 12 1457
[21] Wang X Y Zhang Y Q Zhao Y Y Nonlinear Dyn. 82 1269
[22] Sui L S Gao B Opt. Laser Technol. 48 117
[23] Wang Z Huang X Li Y X Song X N 2013 Chin. Phys. 22 010504
[24] Saberikamarposhti M Mohammad D Rahim M S M et al. 2014 Nonlinear Dyn. 75 407
[25] Watson J D Crick F H C 1953 Nature 171 737
[26] Zhou N R Pan S M Cheng S et al. 2016 Opt. Laser Technol. 82 121
[27] Wang X Y Zhang H L 2015 Opt. Commun. 342 51
[28] Wei X P Guo L Zhang Q et al. 2012 J. Syst. Software 85 290
[29] Tong X J Wang Z Zhang M et al. 2015 Nonlinear Dyn. 80 1493
[30] He S B Sun K H Wang H H 2014 Acta Phys. Sin. 63 030502 in Chinese