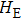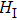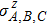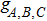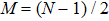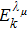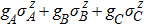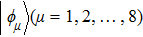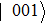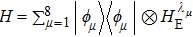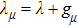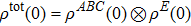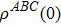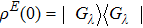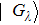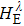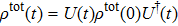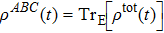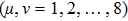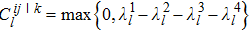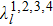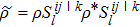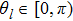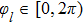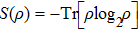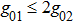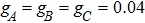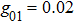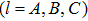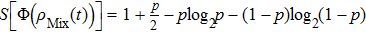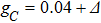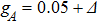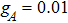1. IntroductionQuantum correlations rooted in the superposition principle of quantum mechanics, constitute a fundamental resource for the quantum information processing.[1–5] As a measerment of the quantum correlation, quantum discord[6] can demonstrate more general nonclassical correlation than the quantum entanglement, and therefore has been attracted much attention. For the quantum states coupled to external environments, quantum discord may be nonzero in separable states and has been used to implement some quantum tasks, such as quantum remote state preparation,[7] quantum phase transitions (QPTs) detections,[8–13] and various other quantum systems.[14–17]
Generally the quantum correlations of a qubits system are fragile and will eventually vanish on account of the external environments. Such decoherence processes are the main obstacle in the development of quantum technology. Thus many researchers have studied the dynamics of quantum correlations under the influence of various environments,[11–22] in order to keep the quantum correlation by tailoring the system-environment coupling. In a multi-body environment, such as a spin-chain system, the QPTs may dominate the decoherence process. Therefore, much attention has been paid to study the decoherence of a quantum system coupled to a spin environment with QPTs.[11,12,17–20,23–30] For the two-qubit and three-qubit systems coupled to the anisotropic XY chain, the dynamical processes of entanglement and quantum discord have been discussed at the critical points of QPT. The results show that the decoherence processes of quantum correlations are accelerated by the quantum criticality, which are significant to witness the critical point of QPTs and understand the dynamics of quantum correlations. In particular, some researchers[27–30] revealed that the entanglement and quantum discord of three-qubit system coupled to XY spin-chain environment generally decay to zero at the QPT under weak coupling regime. They also pointed out that the W state is a decoherence-free state when the coupling strengths are uniform. Motivated by this, we realize that the coupling strengths between each qubit and environment may dominate the dynamical behavior of quantum correlations. We investigate, in details, the role played by coupling strengths in the evolution of entanglement and quantum discord for the pure W and the mixed state (GHZ and W state) under an XY quantum-critical environment. We demonstrate that a remarkable quantum correlation can be retained at a certain configuration of the three coupling strengths.
This paper is organized in the following way. In Section 2, we briefly introduce the physical model and corresponding Hamiltonian evolution. In Section 3, we firstly present the measurement formulae of the entanglement and quantum discord for three-qubit system. Then by means of two variation modes of three coupling strengths, the evolutions of entanglement and quantum discord for the three-qubit system coupled to an XY spin-chain environment are investigated at the critical point of the QPT. Finally, we summarize our results in Section 4.
2. Physical model and Hamiltonian evolutionThe total Hamiltonian of three-qubit system[27–30] transversely coupled to an XY spin-chain environment includes two parts,  , they take the following expressions (we take
, they take the following expressions (we take  )
)
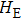
describes the self-Hamiltonian of the XY spin-chain environment, and
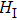
represents the interaction Hamiltonian between the three-qubit system and the spin chain. The Pauli operators
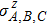
and

are used to describe the three-qubit system and the spin-chain environment. The parameter
λ characterizes the strength of the transverse field,
N is the total number of the sites of the spin chain,
γ is the anisotropy parameter, and
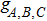
are coupling strengths between the each qubit and the environment.
By successively using Jordan–Wigner, Frouier and Bogoliubov transformations, we diagonalise the projected Hamiltonian  as
as
with

, and
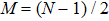
, the
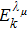
represents energy spectrum. On the other hand, the eigenstates of the operator
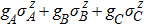
can be denoted by
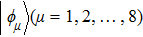
, and written by

,
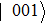
, …,

. Then the total Hamiltonian is rewritten as
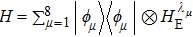
, and
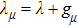
can be expressed as
We suppose the density matrix of the total system is
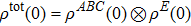
, where
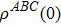
is the initial density matrix of the three-qubit system,
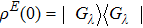
is the initial density matrix of the XY spin-chain environment, and
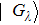
is the ground state of
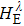
. The subsequent time evolution of the total system is determined by
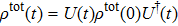
. One can obtain the reduced density matrix of the three-qubit system by tracing over the environment, denoted by
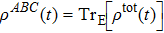
. We can give the following equation
where

is the projected time evolution operator. The decoherence factor is

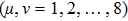
. Therefore, we can analyze the evolution of entanglement and quantum discord for the three-qubit system by means of the reduced density matrix
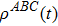
.
3. The evolution of entanglement and quantum discordFor the three-qubit system, the GHZ state and W state are often selected as valuable examples to study the significant properties of various physical quantities.[31–33] Hence we set the initial state of three-qubit system as W state and mixed state (i.e., W and GHZ states) in this paper. For the GHZ state, we can find that the parameters λ1 and λ8 only depend on the sum of three coupling strengths and do not perceive the differences between any pair of the parameters gA, gB, and gC. Hence, the internal changes of three coefficients cannot affect the dynamics of quantum corrections. On the contrary, the parameters λ2, λ3, and λ5 are quite sensitive to the differences among gA, gB, and gC, then the inhomogeneity of the system-environment coupling must make a large effect on the evolution of the quantum correlations for W and mixed state under the XY quantum-critical environment. Therefore, for three-qubit system coupled to spin-chain environment, we discuss the effect of the internal change of three coupling parameters with fixed sum on the evolution of the entanglement and quantum discord for the pure W state and the mixed state. It is worth noting that we only study the dynamics of tripartite quantum correlations at the critical point of quantum phase transition for the spin environment.
We firstly present the measurement formulae of the entanglement and quantum discord for the three-qubit system. For the multipartite entanglement, several references proposed the lower bounds of concurrence to characterize the entanglement of multipartite states.[34,35] For a three-qubit system, a lower bound of concurrence can be expressed as[35]
where each term

is expressed as
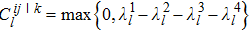
,
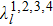
are the square roots of nonzero eigenvalues of the matrix
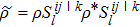
in decreasing order.
[29,35] Furthermore, Rulli and Sarandy have proposed a global quantum discord by means of a systematic extension of the bipartite quantum discord.
[36] For a three-qubit state, the global quantum discord has the following expression,
with the angles
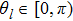
and
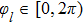
, the
l = 1,2,3 correspond to subsystems
A,
B, and
C, respectively.
ρA,
ρB, and
ρC are the reduced density matrices of three-qubit system,
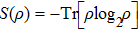
is the von-Neumann entropy of the density matrix.
(i) The W stateWe assume that the initial state is W state  , which has the maximum tripartite coherence.[33] According to Eq. (5), we can obtain the reduced density matrix of the three-qubit system. Making use of the definition of the lower bound of concurrence from Eq. (6), we can obtain
, which has the maximum tripartite coherence.[33] According to Eq. (5), we can obtain the reduced density matrix of the three-qubit system. Making use of the definition of the lower bound of concurrence from Eq. (6), we can obtain
We take into account the definition of the global measure of quantum discord in three-qubit system from Eq. (
7). For the pure W state, because the

has no analytical solution, we can only give the form of quantum discord as
Many investigations indicate that the lower bound of concurrence and quantum discord can witness the quantum criticality of the spin environment under weak-coupling regime as the three-qubit system is coupled to spin-chain environment.[27–30] The coupling strengths characterize the details of interaction between the central system and surrounding environment, so they affect directly the dynamical process of the quantum system. Hence, we assume the sum of three coupling parameters is constant and give two variation modes of three coefficients, mode 1:  ,
,  ,
,  , and
, and  ; mode 2:
; mode 2:  ,
,  ,
,  ,
,  , and
, and 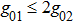 , where
, where  . With these two tailoring schemes, all the possible variations of the coupling strengths can be set by changing four parameters. We obtain some interesting results from this scenario.
. With these two tailoring schemes, all the possible variations of the coupling strengths can be set by changing four parameters. We obtain some interesting results from this scenario.
Figure 1 shows the dynamics of quantum correlations for W state at critical point (i.e.,  ) with the first variation mode with
) with the first variation mode with  and
and  . If
. If  , then
, then 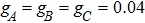 , and
, and  , the W state can be regarded as a decoherence-free state,[27–30] the entanglement is
, the W state can be regarded as a decoherence-free state,[27–30] the entanglement is  and quantum discord is
and quantum discord is  . When the absolute value of
. When the absolute value of  becomes larger, the entanglement and quantum discord vanish quickly at the critical point of QPT. We can conclude that quantum correlations become more robust as the system–environment coupling is more homogeneous, but will eventually decay to zero for long enough time except three coupling coefficients are identical. In this case, the dynamical behaviors of both entanglement and quantum discord are completely symmetric (see also Fig. 4). The coupling parameters gB and gC have equal-weighted effect on the dynamics of the entanglement and quantum discord.
becomes larger, the entanglement and quantum discord vanish quickly at the critical point of QPT. We can conclude that quantum correlations become more robust as the system–environment coupling is more homogeneous, but will eventually decay to zero for long enough time except three coupling coefficients are identical. In this case, the dynamical behaviors of both entanglement and quantum discord are completely symmetric (see also Fig. 4). The coupling parameters gB and gC have equal-weighted effect on the dynamics of the entanglement and quantum discord.
Figure 2 illustrates the dynamics of quantum correlations for W state at critical point (i.e.,  ) with the second variation mode:
) with the second variation mode: 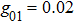 ,
,  , and
, and  . Firstly, one can observe similar dynamical process for the lower bound of concurrence and quantum discord, each quantum correlation dynamics shows three peaks as Δ = −0.03, Δ = 0.0, and Δ = 0.03. The peaks do not evolve with time. We take entanglement for example to analyze the reason for large nonzero entanglement. When Δ = 0.0, we can get
. Firstly, one can observe similar dynamical process for the lower bound of concurrence and quantum discord, each quantum correlation dynamics shows three peaks as Δ = −0.03, Δ = 0.0, and Δ = 0.03. The peaks do not evolve with time. We take entanglement for example to analyze the reason for large nonzero entanglement. When Δ = 0.0, we can get  , i.e., the B and C qubits are coupled to environment with the same coupling strengths. Then
, i.e., the B and C qubits are coupled to environment with the same coupling strengths. Then  for arbitrary time t, while the other two decoherence factors
for arbitrary time t, while the other two decoherence factors  and
and  will decay to zero with time. The final peak value is
will decay to zero with time. The final peak value is  by calculating Eq. (8). In the same way, the other two peaks are
by calculating Eq. (8). In the same way, the other two peaks are  and
and  for Δ = −0.03 and Δ = 0.03. The above discussions are also used to explain the dynamical behavior of quantum discord. Figure 3 shows the more detailed information about Δ = −0.03, Δ = 0.0, and
for Δ = −0.03 and Δ = 0.03. The above discussions are also used to explain the dynamical behavior of quantum discord. Figure 3 shows the more detailed information about Δ = −0.03, Δ = 0.0, and  , which correspond to three different combinations of gA, gB, and gC. It is found that two quantum correlations firstly undergo a rapid decay in a short time and then become nonzero constants. In a word, we conclude that the coupling strengths between qubits system and XY spin chain strongly impact the quantum correlations dynamics. We can obtain the nonzero quantum correlations when any two of the three coupling strengths are identical.
, which correspond to three different combinations of gA, gB, and gC. It is found that two quantum correlations firstly undergo a rapid decay in a short time and then become nonzero constants. In a word, we conclude that the coupling strengths between qubits system and XY spin chain strongly impact the quantum correlations dynamics. We can obtain the nonzero quantum correlations when any two of the three coupling strengths are identical.
In addition, we also test whether three coupling parameters play the equivalent role in the evolution of the entanglement and quantum discord. We exchange and shuffle the three coupling strengths. For example, with respect to the first variation mode of three coupling strengths, we consider the other two cases:  ,
,  , and
, and  ,
,  . For three cases of the first variation mode, figure 4 shows that two quantum correlations show unimodality and good symmetry at t = 5 (These results are the same for other time). There is a slight deviation for the case
. For three cases of the first variation mode, figure 4 shows that two quantum correlations show unimodality and good symmetry at t = 5 (These results are the same for other time). There is a slight deviation for the case  ,
,  from the other two cases for two quantum correlations. In a word, three coupling strengths have an approximate equal-weighted effect on the evolution of entanglement and quantum discord for the first variation mode. In the same way, we make the same investigation about three cases of the second variation mode, their results deduced from three cases are presented in Fig. 5. One can find that three coupling parameters play the different roles in the evolution of entanglement and quantum discord. This is because three cases of the second variation mode lead to the change of parameters λ2, λ3, and λ5, and the decoherence factors
from the other two cases for two quantum correlations. In a word, three coupling strengths have an approximate equal-weighted effect on the evolution of entanglement and quantum discord for the first variation mode. In the same way, we make the same investigation about three cases of the second variation mode, their results deduced from three cases are presented in Fig. 5. One can find that three coupling parameters play the different roles in the evolution of entanglement and quantum discord. This is because three cases of the second variation mode lead to the change of parameters λ2, λ3, and λ5, and the decoherence factors  ,
,  , and
, and  . In view of Eq. (8), we know clearly the reason of the shift of peaks for the entanglement. The above reason is suitable to explain the dynamical behavior of the quantum discord. In these cases the exchanges only happen in the positions of the peak but the shapes and peak values are not changed. In short, we can conclude that the role of each coupling parameter in the quantum correlations dynamics strongly depend on the variation mode of three coupling coefficients.
. In view of Eq. (8), we know clearly the reason of the shift of peaks for the entanglement. The above reason is suitable to explain the dynamical behavior of the quantum discord. In these cases the exchanges only happen in the positions of the peak but the shapes and peak values are not changed. In short, we can conclude that the role of each coupling parameter in the quantum correlations dynamics strongly depend on the variation mode of three coupling coefficients.
(ii) The mixed stateWe assume that the three-qubit system is initially in the mixed state which consists of the GHZ state and W state ( , p is the probability of the mixed state being in the W state). Taking into account the definition of lower bound of the concurrence from Eq. (6), we can obtain the analytic expression,
, p is the probability of the mixed state being in the W state). Taking into account the definition of lower bound of the concurrence from Eq. (6), we can obtain the analytic expression,
According to Eq. (
7), we can obtain the lowest value of the quantum discord by

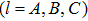
and
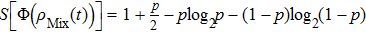
. We can only give the form of the quantum discord as
In Fig.
6, the lower bound of concurrence and quantum discord of the mixed state as a function of the magnetic intensity
λ and time
t are plotted. One can observe that the entanglement and quantum discord decay more sharply at the critical point of the QPT (i.e.,

). However, compared to quantum discord, the effect of quantum criticality on the evolution of entanglement can be concentrated in a narrower region near the critical point, which indicates that the evolution of entanglement witnesses the quantum criticality of the spin environment more efficiently. It is then natural to ask what dynamical behavior the quantum correlations show at the critical point of QPT when the probability of the system being in the W state changes. So we will discuss quantum correlations dynamics at the critical point of QPT for arbitrary probability parameter
p. Figure
7 shows the concurrence and quantum discord of the mixed state as a function of time
t and probability parameter
p. We find that the entanglement and quantum discord are sustained longer for the larger probability parameter
p, which manifests that the W state is more robust than the GHZ state under the spin environment. For the lower bound of concurrence, it is found that initial entanglement is minimum as the probability parameter
p is about 0.55, while for the quantum discord, the initial value changes from 1.0 to 1.5 with the increasing of the probability parameter
p.
In the following section, we investigate the effect of the different variation modes of three coupling parameters on the quantum correlations dynamics of the mixed state. For the variation mode 2, ( ,
,  , and
, and  ), we can see from Fig. 8 that there is a completely different dynamical behavior for the lower bound of entanglement and quantum discord at the critical point of QPT. Here, we set the probability parameter p to 0.5, then the evolution of the quantum discord becomes insensitive to the variable Δ. The nonzero quantum discord are always retained regardless of the coupling strengths between the qubits system and spin-chain environment, while the nonzero entanglement can only be obtained with two identical coupling strengths, such as Δ = 0.0
), we can see from Fig. 8 that there is a completely different dynamical behavior for the lower bound of entanglement and quantum discord at the critical point of QPT. Here, we set the probability parameter p to 0.5, then the evolution of the quantum discord becomes insensitive to the variable Δ. The nonzero quantum discord are always retained regardless of the coupling strengths between the qubits system and spin-chain environment, while the nonzero entanglement can only be obtained with two identical coupling strengths, such as Δ = 0.0  . It indicates that quantum discord may be nonzero even for separable states at the probability parameter p = 0.5.
. It indicates that quantum discord may be nonzero even for separable states at the probability parameter p = 0.5.
Let us turn to study the effects of the other probability parameters p on quantum correlations dynamics. In Fig. 9, we set the time as t = 15 and plot the lower bound of the entanglement and quantum discord of the mixed state as a function of the variable Δ for four different probability parameters (p = 0.0 represents GHZ state). The entanglement and quantum discord show different dynamical behaviors for the same probability parameter p. Firstly, for the entanglement, three peaks become larger with the increasing of the probability parameter p, which can be seen from Eq. (10). Again, the entanglement will vanish with time except the cases of two identical coupling strengths. It implies that three peaks will become narrower along the time. On the other hand, there is a conversion of valleys to crests with the increasing of the probability parameter p for the quantum discord. Most of all, although the quantum discord of the mixed state is oscillatory with different variable Δ, it finally retain a stable nonzero quantum correlation which is immune to the spin chain environment. For example, when the probability parameter p is equal to 0.8, we have plotted the quantum discord versus time t for five different values of variable Δ (Δ = −0.03, −0.015, 0.0, 0.015, and 0.03), we find that the quantum discord of the mixed state always retain a stable nonzero quantum correlation (QD=0.551, 0.334, 0.551, 0.334, and 0.4).
We also make an investigation about the effect of the first variation mode ( , and
, and  ) on the quantum correlations dynamics. In Fig. 10, we can observe that there is a single crest for the entanglement and quantum discord as three coupling strengths take the same value and the peak becomes larger with the increasing of the probability parameter p. Taking into account the initial entanglement and quantum discord from Fig. 7, we can see that the mixed state is not a decoherence-free state any more. Remarkably, we once again find that quantum discord of the mixed state finally retain nonzero value regardless of the interaction between the central qubits system and environment, while the entanglement will decay to zero except the condition that three coupling strengths take the same value. Namely, the quantum discord of disentangled mixed state can keep nonzero constants. Therefore, we make sure that the quantum discord is more robust than entanglement for the mixed state exposed to the spin environment. The non-vanishing quantum discord is an important resource for quantum information processing.
) on the quantum correlations dynamics. In Fig. 10, we can observe that there is a single crest for the entanglement and quantum discord as three coupling strengths take the same value and the peak becomes larger with the increasing of the probability parameter p. Taking into account the initial entanglement and quantum discord from Fig. 7, we can see that the mixed state is not a decoherence-free state any more. Remarkably, we once again find that quantum discord of the mixed state finally retain nonzero value regardless of the interaction between the central qubits system and environment, while the entanglement will decay to zero except the condition that three coupling strengths take the same value. Namely, the quantum discord of disentangled mixed state can keep nonzero constants. Therefore, we make sure that the quantum discord is more robust than entanglement for the mixed state exposed to the spin environment. The non-vanishing quantum discord is an important resource for quantum information processing.