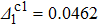† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11504102), the Scientific Research Items Foundation of Hubei Educational Committee, China (Grant Nos. Q20161803 and B2016091), the Doctoral Scientific Research Foundation (Grant No. BK201407), and the Major Scientific Research Project Pre-funds of Hubei University of Automotive Technology, China (Grant No. 2014XY06).
The transport property and phase transition for a parallel triple dot device are studied by adopting Wilson's numerical renormalization group technique, focusing on the effects of level spacings between neighboring dot sites. By keeping dot 2 at the half-filled level and tuning the level differences, it is demonstrated that the system transits from local spin quadruplet to triplet and doublet sequently, and three kinds of Kondo peaks at the Fermi surface could be found, which are separated by two Kosterlitz–Thouless type quantum phase transitions and correspond to spin–3/2, spin–1, and spin–1/2 Kondo effect, respectively. To obtain a detailed understanding of these problems, the charge occupation, the spin—spin correlation, the transmission coefficient, and the temperature-dependent magnetic moment are shown, and necessary physical arguments are given.
For the last several years, systems of coupled multi-quantum dots have gained significant interests both experimentally[1–6] and theoretically, due to rapid progress in spintronics[7–9] and quantum information.[10,11] An important example of a multi-dot system is the triple quantum dots (TQD). Such structure exhibits many interesting quantum phenomena in the strong correlation limit. For instance, the Aharanov–Bohm (AB) effect and magnetic frustration are studied in systems with triangular geometry,[12–15] and the multi-channel Kondo effect related to a number of Fermi-liquid and non-Fermi-liquid behaviors are investigated in various TQD models.[16–20] Furthermore, TQD systems are also considered as ideal models to show the Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction,[21,22] the quantum interference,[23–26] and various kinds of quantum phase transition (QPT).[13,15,27–32] Basically, these behaviors depend closely on the organizations of the quantum dots and the conduction leads, as well as the coupling/interaction elements which have been taken into account.
Within the above phenomena, the level difference plays an important role as suggested in some double quantum dot (DQD) structures. For instance, a local spin triplet–singlet transition of Kosterlitz–Thouless (KT) type is found as the difference increases.[33] For a parallel DQD system, it is revealed that the triplet–doublet transition could be KT type or first order depends on the breaking of the spin-rotation SU(2) symmetry,[34] and the linear conductance is shown to have an asymmetric line shape of the Fano resonance when the interdot tunneling coupling is taken into account.[35] In a spinless two-level dot system, charge oscillation occurs in the presence of level spacing as the gate voltage sweeps.[36] These works are limited in the double dot structures, but less is studied in the TQD system. Compared to the double dot system, TQD structure exhibits more attractive behaviors, owing to its complex geometry and much more Feynman paths for the electron transmission.[25] Furthermore, experimentally speaking, scaling up the number of spin-1/2 qubits is an inevitable step towards the realization of quantum computation, not only for extending the qubit system, but also for performing practical quantum algorithms.[37] Very recently, plenty of experimental works have been carried out on this topic in TQD systems,[5,6,38–41] therefore, to illustrate the electronic transport, phase transition and relevant quantum phenomena in such systems also becomes an emergent task.
In this paper, we consider a parallel TQD system with level spacings between neighboring dot sites. With the help of the numerical renormalization group (NRG) method, and fixing dot 2 at the half-filled level, we demonstrated that the level spacings play important roles in the linear conductance and the QPT. Our main findings include the following: by tuning the level differences, the ground state of the system transits from local spin quadruplet to triplet, then doublet sequentially, and three kinds of Kondo peaks at the Fermi surface could be found, corresponding to spin-3/2, spin-1, and spin-1/2 Kondo effect, respectively. Two Kosterlitz–Thouless (KT) type transitions are clarified, resulting from asymmetric Kondo couplings between conduction leads and different dots, as well as the unequal charge occupation of three dots. To handle these problems, some important physical quantities are shown, and necessary physical arguments are given.
The outline of the paper is as follows. In Section
We illustrate the second-quantized form of the model Hamiltonian for the triple dot device in Fig.
 |
 |
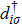
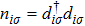
The second part is for the non-interacting electrons in the conduction lead, 


In the following discussion, we concentrate on the quantum behaviors in the strong correlation limit, hence a sophisticated theoretical technique must be adopted. Therefore, we use the celebrated NRG method[42–44] to solve Eq. (
The total charge number Ntot and the local spin Sdot2 are defined as
 |
The linear conductance through the device G is determined by the Landauer formula[45]
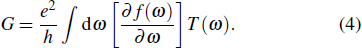 |
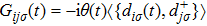
 |
 |
Finally, we define the temperature-dependent magnetic moment of the dots μ2(T) at temperature T as
 |
In this section, we study the phase transition and the electronic transport of the TQD device in the strongly correlated regime, focusing on the phenomena when the level differences sweep upwards. The on-site Coulomb repulsion, the dot-lead coupling, and the charge energy of dot 2 are fixed at U = 0.1, Γ = 0.01, and ε2 = −U/2, respectively, throughout this paper. For convenience, we choose Δ2 = Δ1/2. However, it is worth noting that our conclusions are robust for general cases, and do not really require Δ1 and Δ2 to satisfy the above relation.
Let us start our discussion from the quantum phase transition for the TQD system. In Figs. 

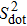
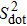
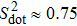
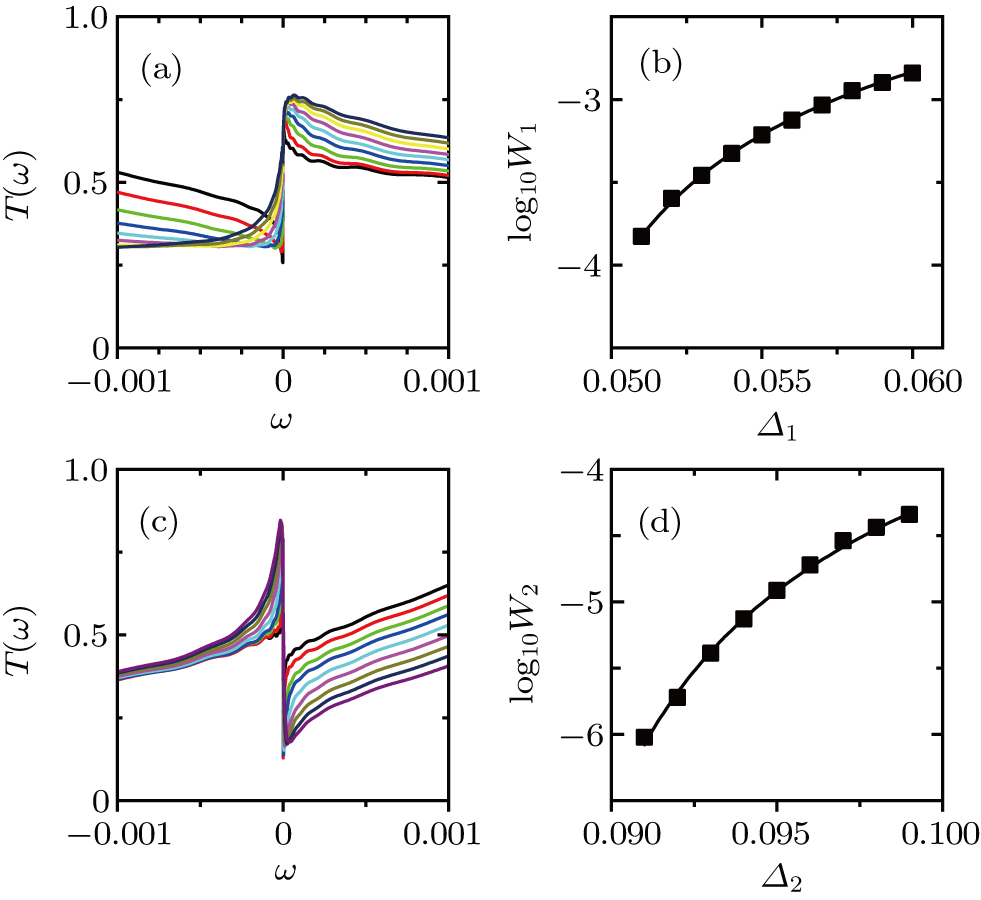
Figures 


 | Fig. 3. (color online) (a)–(c) Transmission coefficient T(ω) at zero temperature for various Δ1. The remaining parameters are the same as in Fig. |
To get more information about the phase transition, we show T(ω) on the triplet side near 


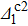

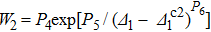
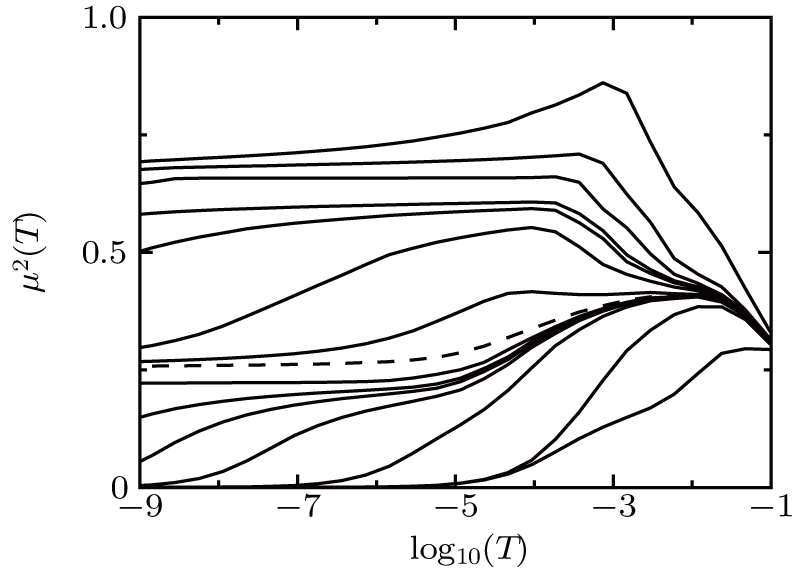
To exhibit more information about the low-temperature scenario, we present μ2(T) for different Δ1 in Fig. 
To explore the physical origination of the KT transitions, we change Eq. (
 |
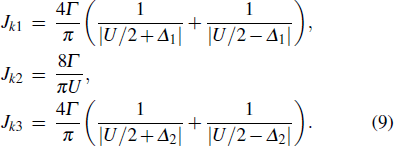 |
With increasing Δ1, Jki are asymmetric. On the other hand, the charge occupation in three dots also become different. The symmetric broken by these features are the origination of the KT transitions, similar to a two-level dot system with level difference[33] and inter-dot Coulomb repulsion.[34] Furthermore, it is worth noting that one can estimate the critical points by considering the energy levels of an isolated TQD model. For instance, the energy level for the spin quadruplet can be written as EQ = ε1 + ε2 + ε3= −3U/2. While that for the triplet is ET = 2ε1 + ε2 + ε3 + U = −U − 3Δ1/2, and the level for the doublet is given by ED = 2ε1 + ε2 + U = −U/2 − 2Δ1. As Δ1 increases, the energy levels for the triplet and the singlet are pulled down, and eventually degenerate with the quadruplet at Δ1 = U/3 and the triplet at U respectively. As a result, two QPTs of the KT type can be found at 

In conclusion, we have studied the phase transition and Kondo behavior in a triple quantum dot device with parallel organization in the strongly correlated regime. We concentrate on the effect of the level differences Δ1 = ε2 − ε1 and Δ2 = ε3 − ε2. By keeping dot 2 at the half-filled level and tuning the level differences, it is shown that the ground state of the system transits from local spin quadruplet to triplet, then doublet sequentially, three kinds of Kondo peaks at the Fermi surface could be found in the transmission coefficient, which correspond to spin-3/2, spin-1, and spin-1/2 Kondo effect, respectively. Two KT type phase transitions are clarified, resulting from asymmetric Kondo couplings between the conduction leads and different dots, as well as unequal electron occupation of three dots. We believe our work not only clarifies the effect of the level difference on the phase transition and the electronic transport in a triple dot structure, but it may also afford useful guidance for spintronics and molecular electronics devices.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] |