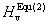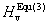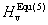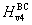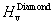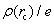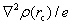† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. U1304111), Program for Science & Technology Innovation Talents in Universities of Henan Province, China (Grant No. 14HASTIT039), and the Innovation Team of Henan University of Science and Technology, China (Grant No. 2015XTD001)
Using the first-principles calculations based on spin density functional theory (DFT), we investigate the structure, elastic properties, and electronic structure of Pnnm-CrB4. It is found that Pnnm-CrB4 is thermodynamically and mechanically stable. The calculated elastic properties such as the bulk modulus, shear modulus, Young’s modulus, and Poisson’s ratio indicate that CrB4 is an incompressible material. Vicker’s hardness of Pnnm-CrB4 is estimated to be 26.3 GPa, which is in good agreement with the experimental values. The analysis of the investigated electronic properties shows that Pnnm-CrB>4 has the metallic character and there exist strong B–B and Cr–B bonds in the compound, which are further confirmed by Bader’s quantum theory of atoms in molecules (QTAIM). Thermodynamic properties are also investigated.
It is an important research to search for the exceptional physical properties in condensed matter physics. Because of their outstanding properties such as high hardness, high electrical conductivity, and better corrosion resistance,[1–3] transitional-metal borides (TMB) represent an exciting case study and have been applied in many applications from creating machining tools to reducing the wear of everyday objects. These materials consist of small, light element B and large, electron-rich transition metals (Cr, Mn, Ru, W,...). The strong directional covalent bonds between the light element boron and the TM result in the high hardness,[4] and the high density of valence electrons from the transition metals can cause the higher bulk modulus under hydrostatic, both of which can enhance TMB against large plastic deformation and lead to increased hardness.
In recent years, many researchers have successfully synthesized many transitional-metal boron compounds, such as OsB2,[5] ReB2,[5] RuB4,[6] and WB4.[7] Among these compounds, TM tetraborides (TMB4) are promising candidates of ultraincompressible and hard materials for their high hardness due to the high content of boron. For example, the hardness of WB4 is found to be 46.2 GPa because of the three-dimensional boron networks.[6] Many researchers have focused on the tetraborides of transition metals with strong covalent bonds, which can improve the abilities to resist shear deformations.[8] While Os, Re, Ru, and W are all noble metals, which hinder their production and application in industry.
As one of the transition metal tetraborides, chromium tetraboride (CrB4) was first synthesized in 1968[9] and reported to have excellent adhesive wear resistance because of the outstanding hardness.[10] CrB4 can also be used as a surface protecting coating because of its good mechanical properties. The single crystal of CrB4 was first obtained by Knappschneider.[11] Liu et al.[12] obtained crystalline, multiphase CrB4 and showed that CrB4 crystallizes in the orthorhombic space group Pnnm, which is closely related to the space group Immm used to describe the orthorhombic structure of CrB4. Recent researches[13] show that Immm-CrB4 is both dynamically and thermodynamically unstable relative to Pnnm-CrB4.
Recently, Knappschneider et al.[14] synthesized Pnnm-CrB4 single crystal, but they did not obtain the elastic moduli of Pnnm-CrB4 from the experiment. They thought that the hardness of Pnnm-CrB4 may be in the range of 43–48 GPa.[14] Wang et al.[13] predicted that the bulk modulus of Pnnm-CrB4 is 232 GPa and CrB4 has a much higher asymptotic hardness of ~ 30 GPa because of the strong three-dimensional Cr–B. The results of Knappschneider et al.[14] and Wang et al.[13] deviate for the hardness of Pnnm-CrB4. In addition, to the best of our knowledge, the electronic and elastic properties have not been reported for the ground state of CrB4.
In this paper, the electronic, mechanical properties and Bader charge of Pnnm-CrB4 are investigated by using the first-principles calculations. The hardness of the CrB4 crystal is estimated theoretically and compared with the two experimental results.[13,14]
The calculation of structural and electronic properties was performed within the generalized gradient approximation (GGA) by using the plane-wave self-consistent field (PWSCF), which is implemented in the Quantum-Espresso package.[15] The calculations were performed with the spin density functional theory. The exchange–correlation term was treated with Perdew, Burke, and Ernzerhof, known as PBE generalized-gradient approximation.[16] The initial crystal structure was taken from Andersson’s result[17] and used for the computations. During the geometric optimization, no symmetry and no restriction were constrained for both the unit cell shape and the atomic positions. A 50 Ry energy cutoff and a 6×6×6 Monkhorst–Pack mesh of k-points were used to ensure the convergence of the total energy within 1 meV per formula unit. To obtain the electronic density of state (DOS), the tetrahedron method with Blochl corrections was used for the Brillouin-zone integration.
Elastic constants were calculated by using the Cambridge serial total energy package (CASTEP) program.[18] The compound was first optimized by using the Broydon–Fletcher–Goldfarb–Shanno (BFGS) method.[19] The ultrasoft pseudo-potential[20] together with the generalized gradient approximation (GGA) proposed by Perdew et al.[16] was adopted. The bulk modulus B and shear modulus G were obtained from the calculated elastic constants Cij. The Vickers hardenss Hv was also estimated. In addition, the Young’s modulus Y and Poisson’s ratio ν were predicted.
CrB4 is in an orthorhombic system with space group Pnnm and its crystal structure[21,22] is shown in Fig.
| Table 1. Experimental and calculated lattice constants and bond lengths (Å) of Pnnm-CrB4 crystal at ambient pressure. . |
 | Fig. 1. (color online) Crystal structures and its atomic numbering of Pnnm-CrB4. The blue and green spheres represent Cr and B atoms, respectively. |
As shown in Fig.
Further calculations were performed to optimize the lattice constants within a given energy cutoff of 50 Ry. The total energy versus the volume is plotted in Fig.
Obviously, the equilibrium volume is much closer to the calculated value 74.987 Å3 and the experimental value 74.798 Å3, which shows that our calculation is reliable. Table
| Table 2. Calculated elastic constants Cij (GPa), bulk moduli B (GPa), shear moduli G (GPa), Young’s moduli E (GPa), the G/B ratio, Poisson’s ratio ν, and Vicker’s hardness Hv (GPa) at ambient pressure, compared with available experimental and theoretical results. The values in parentheses are experimental values and the others are computational values. . |
For the orthorhombic system, 9 independent components of the elastic constants must satisfy the following necessary conditions for mechanical stability:[28]
 |
From Table
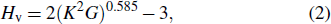 |
In order to have a comparison, the other methods to calculate the hardness of bulk material are also used to calculate the hardness of CrB4. One is Teter’s model[31]
 |
The others are obtained by Jiang et al.[32]
 |
 |
Using Eqs. (
For CrB4, the shear modulus G is 260 GPa, which shows that Pnnm-CrB4 has the strong ability to resist shear change. The low Poisson ratio for Pnnm-CrB4 shows that strong covalent bonding exists in CrB4.[33] Pugh’s ratio of CrB4 is 0.95. The G/B value is often used to assess the brittle or ductile behavior of a compound. Low G/B denotes better ductility, and a critical value of G/B is 0.57.[26] The larger the G/B value, the higher the Vickers hardness. Obviously, the G/B value for Pnnm-CrB4 is much larger than the critical value, so CrB4 can be classified as a brittle material.
In addition, Ba, Bb, and Bc (the bulk moduli along a-, b-, and c-axes) are also calculated according to the method of Nye[34] and their values are 756 GPa, 1209 GPa, and 620 GPa, respectively, which are much larger than those of YB4 (571 GPa, 571 GPa, and 499 GPa).[35] It is noted that the b-axis is less compressible than a- and c-axes because the zigzag boron–boron chains are primarily along the direction. For a- and c-directions, the strengths of the Cr–B and Cr–Cr bonds determine the axial compressibility. In addition, C22 of Pnnm-CrB4 is 936 GPa, which is much larger than the largest component C11 (794 GPa)[36] of d-ZB-C3N4. This indicates that Pnnm-CrB4 may be highly incompressible along the b-axis, which is consistent with the conclusion obtained from the bulk moduli.
In order to check the dynamical stability of Pnnm-CrB4, the phonon dispersion curve is calculated and plotted in Fig.
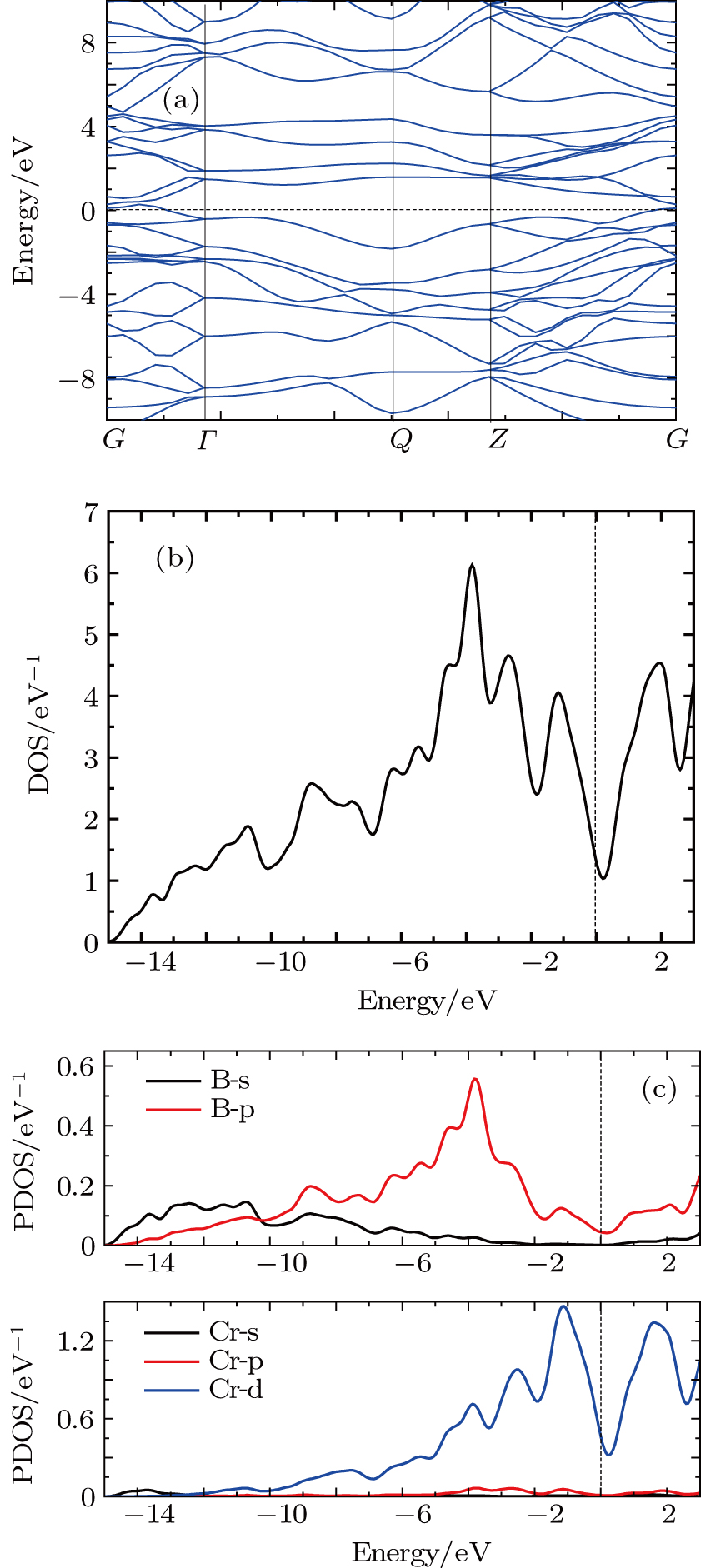
The electronic band structure of Pnnm-CrB4 has been studied along the high-symmetry points of the Brillouin zone and plotted in Fig.
From Figs.
In order to explore the bonding character of Pnnm-CrB4, the electron localization function (ELF) is calculated. The ELF can be used to measure the probability of finding an electron in the neighborhood of another electron with the same spin. The ELF ranges from 0 to 1. ELF = 1 means perfect localization (i.e. a covalent bond), ELF = 0.5 corresponds to the electron-gas like pair probability (i.e., a metallic bond), while ELF = 0 corresponds to no localization (or delocalized electrons). Figure
In Fig.
Table
| Table 3. Partial charge (e) of the Cr and B atoms in Pnnm-CrB4. . |
Based on the topology of the electronic density, Bader’s quantum theory of atoms in molecules (QTAIM) is a useful tool to explain physical and chemical properties of materials. QTAIM analysis[38,39] starts by determining the critical points (CPs) of the electron density, which are classified into maxima, nuclear, or attractor CPs (NCP or n); first-order saddle or bond (BCP or b); second-order saddle or ring (RCP or r); and minima or cage (CP or c). For a predominantly “shared” (covalent) interaction, ρ(r) > 0 and ∇2ρ < 0.[33] In the case of a “closed shell” (ionic) interaction, ρ(r) is usually small (∼10−2 a.u. for an H-bond and ∼10−3 a.u. for a van der Waals’ interaction[39]) whilst ∇2ρ > 0. The sign and magnitude of the total energy density component[40] at a BCP, H(r), are also important parameters of the nature of the bonding[41,42] and can be obtained by the following equation:
 |
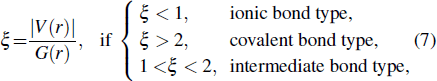 |
It is noted from Table
| Table 4. The crystallographic position and properties of CrB4 electron density bond critical points. . |
Through the quasi-harmonic Debye model, the thermodynamic quantities are calculated for CrB4 from the calculated E–V data at T = 0 and P = 0. Figure
We performed an extensive exploration of the Pnnm-CrB4 crystal in the ground state by using spin density functional theory. Through the analysis of elastic constants and the phonon frequencies, Pnnm-CrB4 is found to be thermodynamically and mechanically stable. The high bulk moduli of Pnnm-CrB4 indicate that Pnnm-CrB4 is an incompressible material. The analysis of the elastic constants indicates that Pnnm-CrB4 may be highly incompressible along the b-axis. The electronic densities of states and electronic localization function analysis have demonstrated that there exist the strong covalent B–B bonding and Cr–B bonds with an intermediate character in the Pnnm-CrB4 crystal. At the Fermi level, there exists a pseudogap of DOS which mainly comes from Cr 3d states and B 2p states. The pseudogap at the Fermi level shows that the bonding between Cr 3d and B 2p starts to be saturated. The analysis of Bader charge indicates that B5, B6, B7, and B8 atoms accept more electrons from Cr1 and Cr2 atoms, when compared with B1, B2, B3, and B4 atoms. The analysis of Bader’s quantum theory of atoms in molecules further confirms the intermediate character of Cr–B bonds. We believe that the current study will advance the understanding of the properties of Pnnm-CrB4 crystal.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] |