† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61475192).
A model of an optical pumping nuclear magnetic resonance system rotating in a plane parallel to the quantization axis is presented. Different coordinate frames for nuclear spin polarization vector are introduced, and theoretical calculation is conducted to analyze this model. We demonstrate that when the optical pumping nuclear magnetic resonance system rotates in a plane parallel to the quantization axis, it will maintain a steady state with respect to the quantization axis which is independent of rotational speed and direction.
The concept of nuclear magnetic resonance (NMR) was proposed by Rabi in 1938.[1] Later, it was improved in theory by Bloch.[2,3] Since then, great progress has been made in NMR. Now, it is widely used in many significant areas such as biological medicine,[4] analytical chemistry,[5,6] fundamental physics,[7–9] and inertial navigation.[10,11]
For a typical optical pumping NMR system shown in Fig.
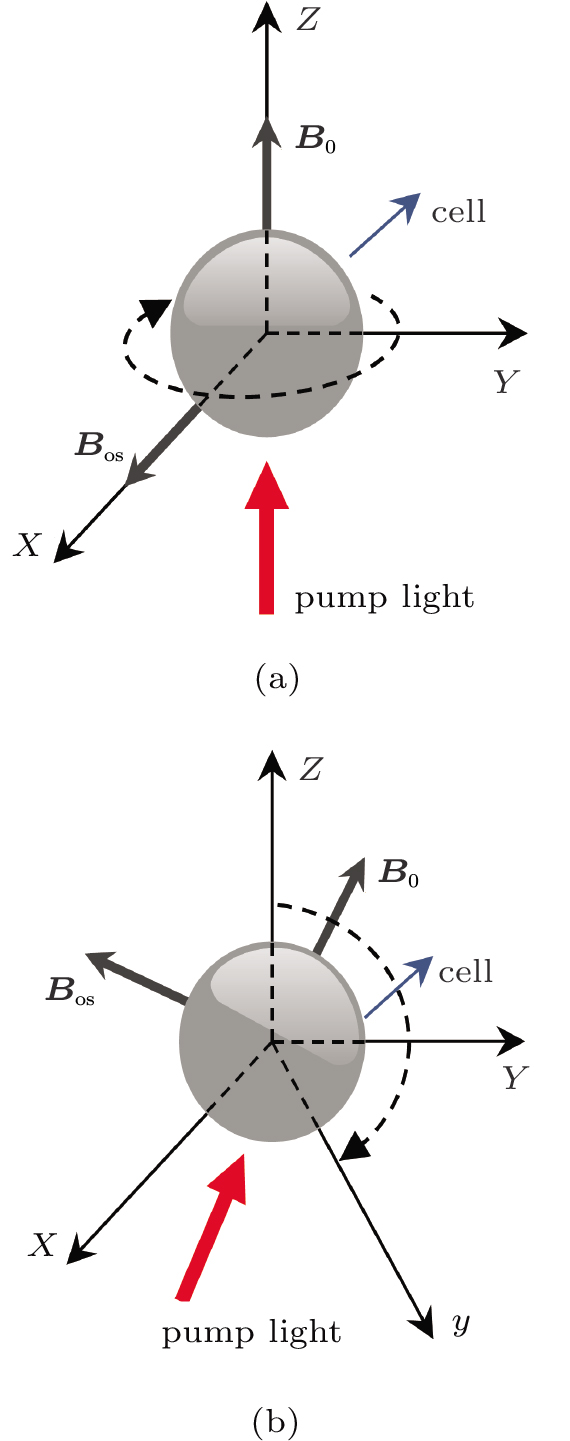 | Fig. 1. (color online) Optical pumping NMR system rotating in a plane (a) perpendicular to the quantization axis or (b) parallel to the quantization axis. |
Since the instability in amplitude of a signal influences the measuring precision of its frequency, and in order to determine the rotation rate of an optical pumping NMR system with high precision, a necessary condition where the system maintains a steady state with respect to the quantization axis is required.[16] When the system rotates around the quantization axis, which is shown in Fig.
For the NMRG (G1) in a three-axis inertial navigation system which consists of three NMRGs, its spin axis is actually the quantization axis which is along the direction of
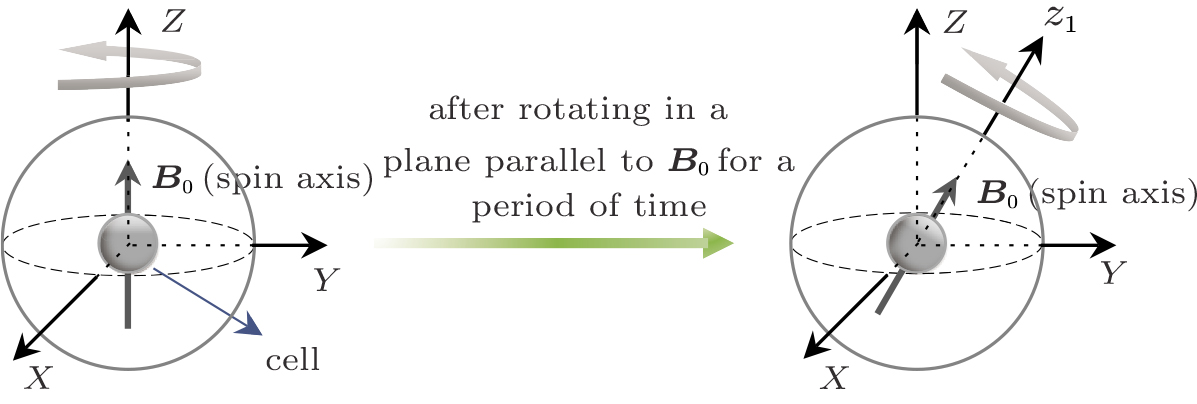 | Fig. 2. (color online) Spin axes of an NMRG before and after rotating in a plane parallel to the quantization axis. |
In this paper, we demonstrate that an optical pumping NMR system will remain steady with respect to the quantization axis when it rotates in a plane parallel to the quantization axis, regardless of any rotational speed and direction.
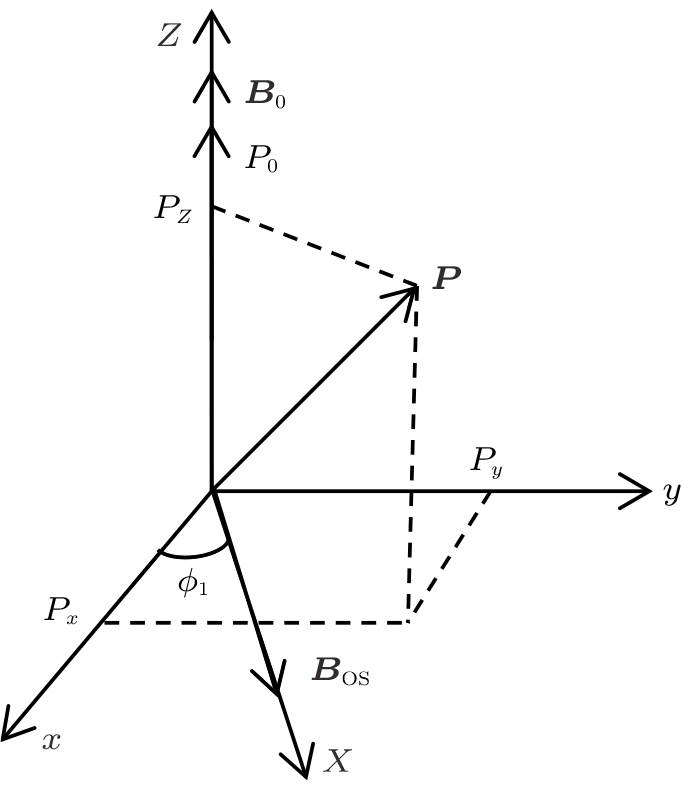
From a macroscopic view, the nuclear spin ensemble is usually described by the magnetization vector M in NMR, which is represented as (MX, MY, MZ)T in the coordinate frame XYZ. When there is no pump light and a constant magnetic field is applied along the Z-axis, under the influence of external magnetic field
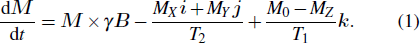 |
 |
In order to simplify the form of Eq. (
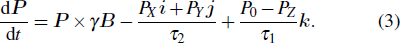 |
For a typical optical pumping NMR system
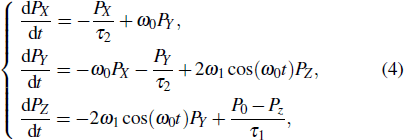 |
The conventional method to simplify the computation of Eq. (
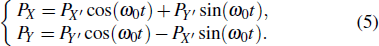 |
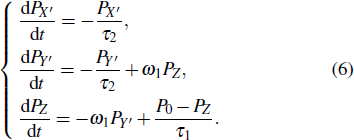 |
When this NMR system reaches a steady state, the above equations are all equal to zero. The stationary solutions can be easily obtained as follows:
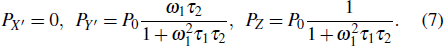 |
From the above analysis, we obtain the stationary state of a typical optical pumping NMR system when its initial quantization axis is along the Z-axis as shown in Fig.
Assume that this NMR system has been steady before t = t0, and it starts to rotate in the y–Z plane with the angular rate of ωr at t = t0, which is shown in Fig.
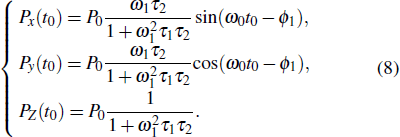 |
When this NMR system rotates around the x-axis in the y−Z plane, the directions of
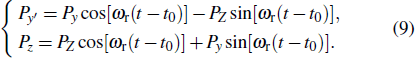 |
Since
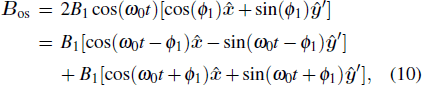 |
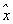
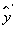
Though this NMR system rotates around the x-axis when t ≥ t0, the evolution of spin polarization vector at any time satisfies the Bloch equation. The directions of pump light and quantization axis are always along the z-axis at any time when t ≥ t0, while the directions of pump light and quantization axis are along the Z-axis when t < t0. So, through the same derivation as for Eq. (
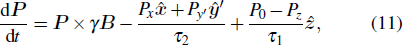 |
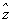


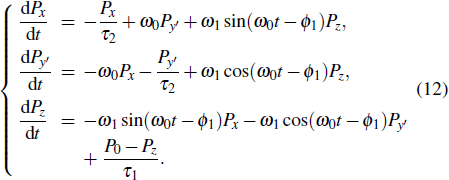 |
Since
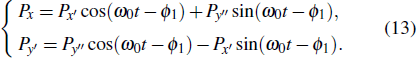 |
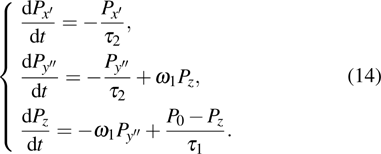 |
When this NMR system reaches a steady state, the above equations are all equal to zero, and the stationary solutions can be obtained as follows:
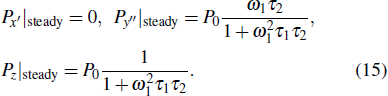 |
Substituting Eqs. (
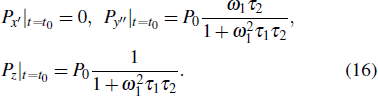 |
We can find from Eqs. (
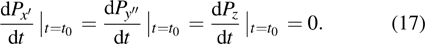 |
Using the knowledge of differential equation in mathematics, the solutions of Px′, Py″, and Pz to Eq. (
 |
From the results of Eq. (
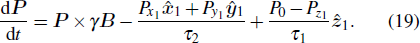 |
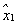
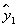
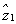
According to the results of Eq. (
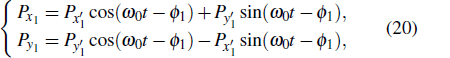 |
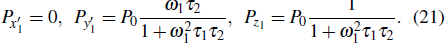 |
By comparing Eqs. (
We can find from the above theoretical calculation that after a typical optical pumping NMR system reaches a steady state, the spin polarization along the quantization axis is a constant no matter how this NMR system rotates, and that is why it can maintain steady. A physical picture of this phenomenon is that the steady state of this NMR system is very special. When this NMR system reaches a steady state and starts to rotate in a certain plane, under the influences of pump light and external magnetic field, both of which rotate with the system, the projection of spin polarization vector on the new quantization axis happens to keep unchanged.
After an optical pumping NMR system reaches a steady state, if it rotates in a plane parallel to the quantization axis with a certain angular rate for a period of time and the quantization axis is now along the z1-axis, then the system will remain steady and it can measure the rotation about the z1-axis. If the system continues to rotate in another plane parallel to the new quantization axis with another angular rate for a period of time and the quantization axis is now along the z2-axis, then the system will remain steady and it can measure the rotation about the z2-axis, since the system is already a steady state when it starts to continue to rotate.
Consequently, when an NMRG is applied to a three-axis inertial navigation system, it can remain steady with respect to the quantization axis when the system rotates in any plane with any angular rate. After the NMRG reaches a steady state and then rotates to a certain orientation, it can measure the rotation about the quantization axis with the same precision as before.
When an optical pumping NMR system rotates in a plane parallel to the quantization axis, the directions of applied magnetic fields and pump light will rotate with the system, while the alkali-metal atoms and noble gas cannot perceive the rotation. Even so, we demonstrate that after this system reaches a steady state, it will maintain steady with respect to the quantization axis when it rotates in a plane parallel to the quantization axis, regardless of any rotational speed and direction. Therefore, for an NMRG applied to a three-axis inertial navigation system, rotation in a plane parallel to the quantization axis has no influence on its measuring precision.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] |