Cite this Article
Wu Jin-Song, Jia Zheng-Mao, Zeng Zhi-Nan. Isolated attosecond pulse generation with few-cycle two-color counter-rotating circularly polarized laser pulses. Chinese Physics B, 2017, 26(9): 093201  
Permissions
Isolated attosecond pulse generation with few-cycle two-color counter-rotating circularly polarized laser pulses
Wu Jin-Song1, 2, Jia Zheng-Mao1, Zeng Zhi-Nan1, †
State Key Laboratory of High Field Laser Physics, Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Shanghai 201800, China
University of Chinese Academy of Sciences, Beijing 100049, China

 

† Corresponding author. E-mail: zhinan_zeng@siom.ac.cn

Project supported by the National Natural Science Foundation of China (Grants Nos. 61690223, 11561121002, 61521093, 11227902, 11404356, and 11574332) and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB16).

Abstract

Most of the schemes for generating isolated attosecond pulses (IAP) are sensitive to the carrier-envelope phase (CEP) of the driving lasers. We propose a scheme for generating IAP using two-color counter-rotating circularly polarized (TCCRCP) laser pulses. The results demonstrate that the dependence of the IAP generation on CEP stability is largely reduced in this scheme. IAP can be generated at most of CEPs. Therefore, the experiment requirements become lower.

PACS: 32.80.Rm;42.65.Ky;42.65.Re
Keyword:isolated attosecond pulse;carrier-envelope phase;two-color counter-rotating circularly polarized laser fields;high-order harmonic generation
1. Introduction

The isolated attosecond pulse (IAP) based on high-order harmonic generation (HHG) is of great importance to study ultrafast electronic dynamics in atoms and molecules. IAP allows for precise control of electron motion with a resolution approaching the atomic unit of time.[1–4] Many schemes for generating IAP have been proposed and investigated.[5–22] However, most of them are sensitive to the carrier-envelope phase (CEP) of the driving laser pulses.[23,24] From the viewpoint of experiments, almost all laser systems cannot maintain the stability of CEP in the long term. Even the passively CEP stabilized optical parametric amplification laser systems can only maintain CEP stability in a specific range.[25,26] Therefore, it is meaningful to find a scheme for generating IAP which is insensitive to, even independent of CEP. Some research has been conducted on this topic.[27,28] Recently, the generation of circularly polarized high harmonics using two-color counter-rotating circularly polarized laser (TC-CRCP) pulses is a fascinating research field.[29–33] In general, circularly polarized laser pulses are independent of CEP. If circularly polarized laser pulses can be used to generate IAP, the generated IAP may also be independent of CEP.

Mid-infrared (MIR) optical parametric amplification light sources have emerged in laboratories.[34–38] Some research on HHG has also been conducted using few-cycle MIR laser pulses.[8,22,23,39–43] In this work, we further theoretically study the IAP generation using few-cycle TC-CRCP laser pulses and investigate the dependence of IAP on CEP of the driving laser pulses, finding that IAP can be generated at most of CEPs, although at some CEP, the intensity of IAP is weaker. The CEP dependence of the IAP generation is much reduced, which thus reduces the requirements for the lasers in experiments.

2. Model and numerical method

We calculate the response of a helium-like model exposed to the laser field synthesized by two counter-rotating circularly polarized pulses at fundamental frequency ω (1800 nm) and second harmonic frequency 2ω (900 nm), respectively. The synthesized laser field in the x and y directions can be respectively presented as follows:

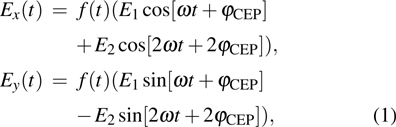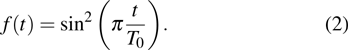where E1 and E2 are the amplitudes of the fundamental pulse and the sencond harmonic pulse, respectively, φCEP is the CEP, and f(t) is the envelope, which can be expressed as
Here T0 = 32.97 fs is the whole time calculated. The full width at half maximum (FWHM) of both lasers is 12 fs (two optical cycles for the fundamental pulse and four optical cycles for its second harmonic). The fundamental pulse rotates counter-clockwise (+), while the second harmonic pulse rotates clockwise (−).

The high-order harmonic spectrum can be obtained by numerically solving the following time-dependent Schrödinger equation (TDSE):

where is the reduced Plank constant, e is the electron charge, m is the mass, V (x,y) is the two-dimension model potential, and Ex (t) and Ey (t) are the x-direction and y-direction electrical fields of the driving laser pulses, respectively. The two-dimension model potential can be written as
Here Z = 1 is the charge of the ion and a = 0.1 is the softening parameter, corresponding to the ground state energy − 0.8285 a.u., which is close to the ionization potential of the helium atom.

3. Results and discussion

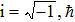
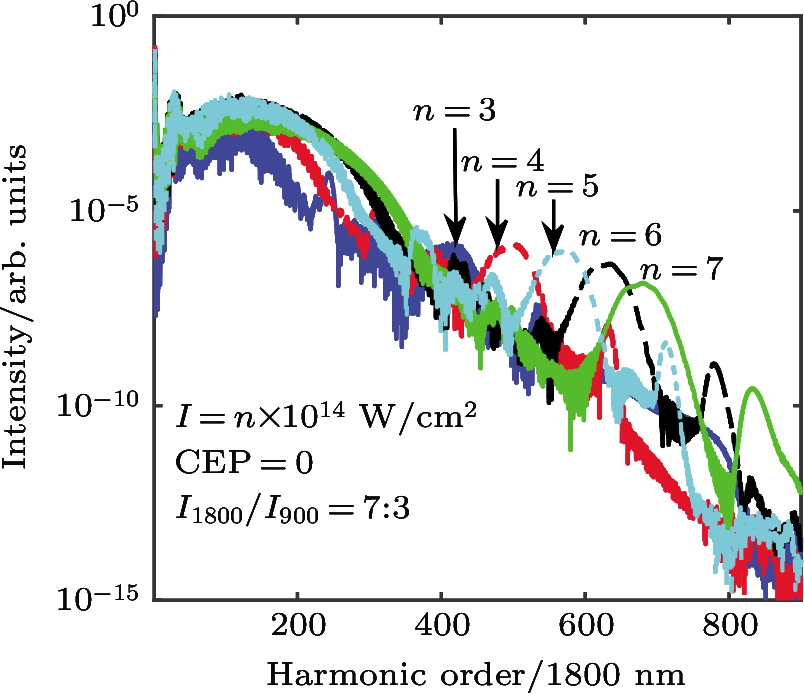
During this work, we keep the intensity ratio between the fundamental pulse and its second harmonic as 0.7:0.3. The harmonic spectra under different total laser intensities are shown in Fig. 1.

Fig. 1. (color online) Harmonic spectra under different total intensities of driving lasers.

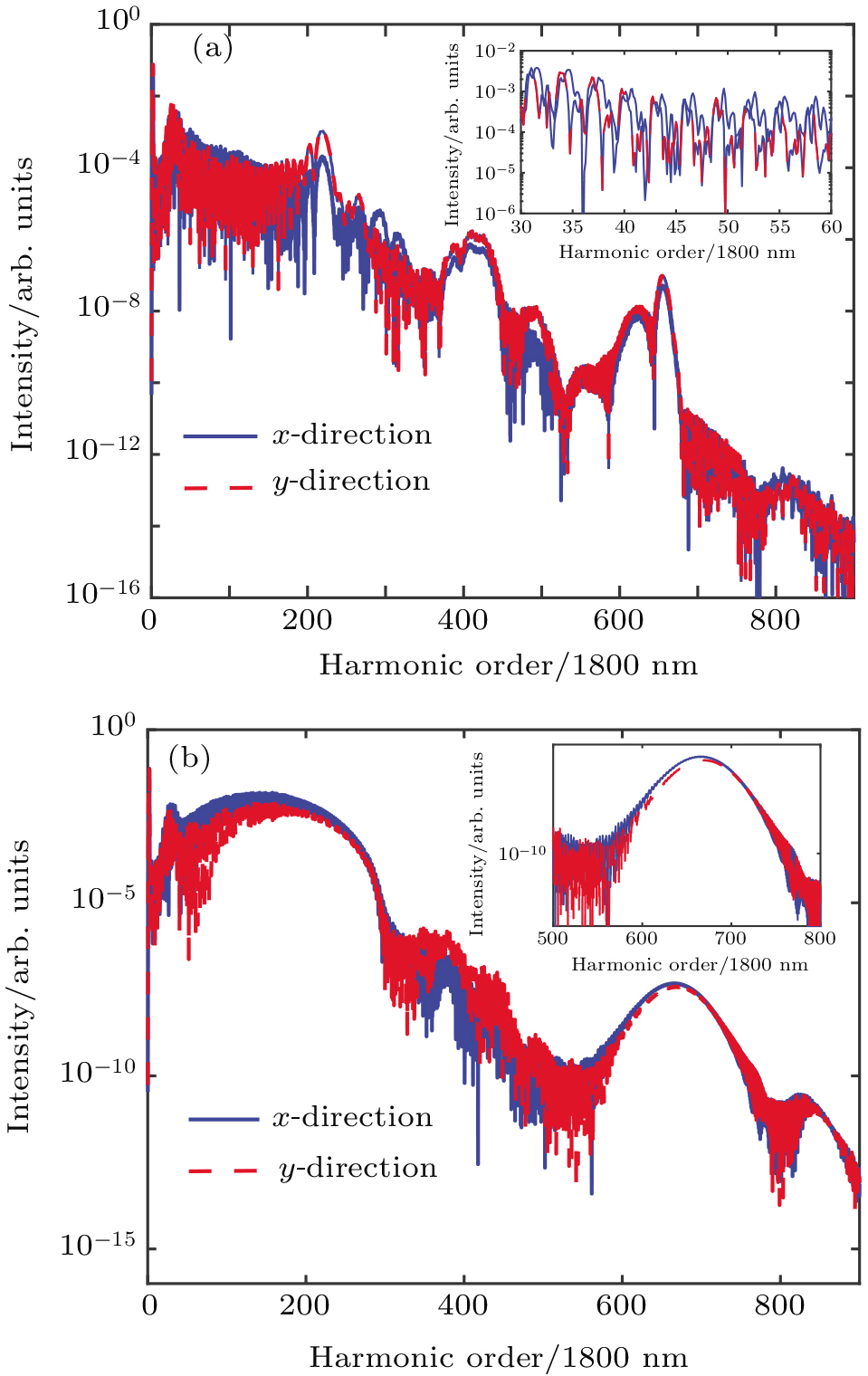
The harmonic spectra are very complex due to the complexity of the electron motion in two directions in the few-cycle TC-CRCP laser pulses. The first plateau is much shorter than the conventional plateau which reaches 3.17Up in linearly polarized laser pulse.[1] With increasing laser intensity, the second plateau gradually appears, on which a continuum harmonic spectrum is produced. Under the total laser intensity of 5 × 1014 W/cm2 (3.5 × 1014 W/cm2 for the fundamental laser and 1.5 × 1014 W/cm2 for the second harmonic), a clear continuum hump with harmonic orders of 500–700 is produced, which can be used to directly synthesize an IAP with the FWHM duration of about 280 as. In the following simulation, the total laser intensity of 5 × 1014 W/cm2 is maintained.

Figure 2 shows the typical harmonic spectra generated by the laser field of 5 × 1014 W/cm2 with different delays between the two-color laser pulses. Figure 2(a) shows the harmonic spectrum when the delay is 0. The inset shows that the harmonics at the orders of 3n (n is a positive integer) have not been generated at low harmonic orders, which is consistent with the former works.[30,31] However, under a specific delay between the fundamental and the second harmonic fields, a supercontinuum appears. Figure 2(b) shows the harmonic spectrum generated when the fundamental laser pulse is 7T / 16(T is the cycle of the fundamental pulse) ahead of the second harmonic. As shown in the inset of Fig. 2(b), IAP can be synthesized by selecting the harmonics from the 500th to the 800th orders. The simulation results show that this supercontinuum can be used to generate an IAP with a pulse duration of about 250 as.

Fig. 2. (color online) High-order harmonic spectra generated by TC-CRCP laser pulses. The delay between the fundamental driving laser pulse and the second harmonic pulse is 0 in panel (a), and 7T/16 in panel (b). The insets are magnifications of some harmonic orders of the corresponding figures.

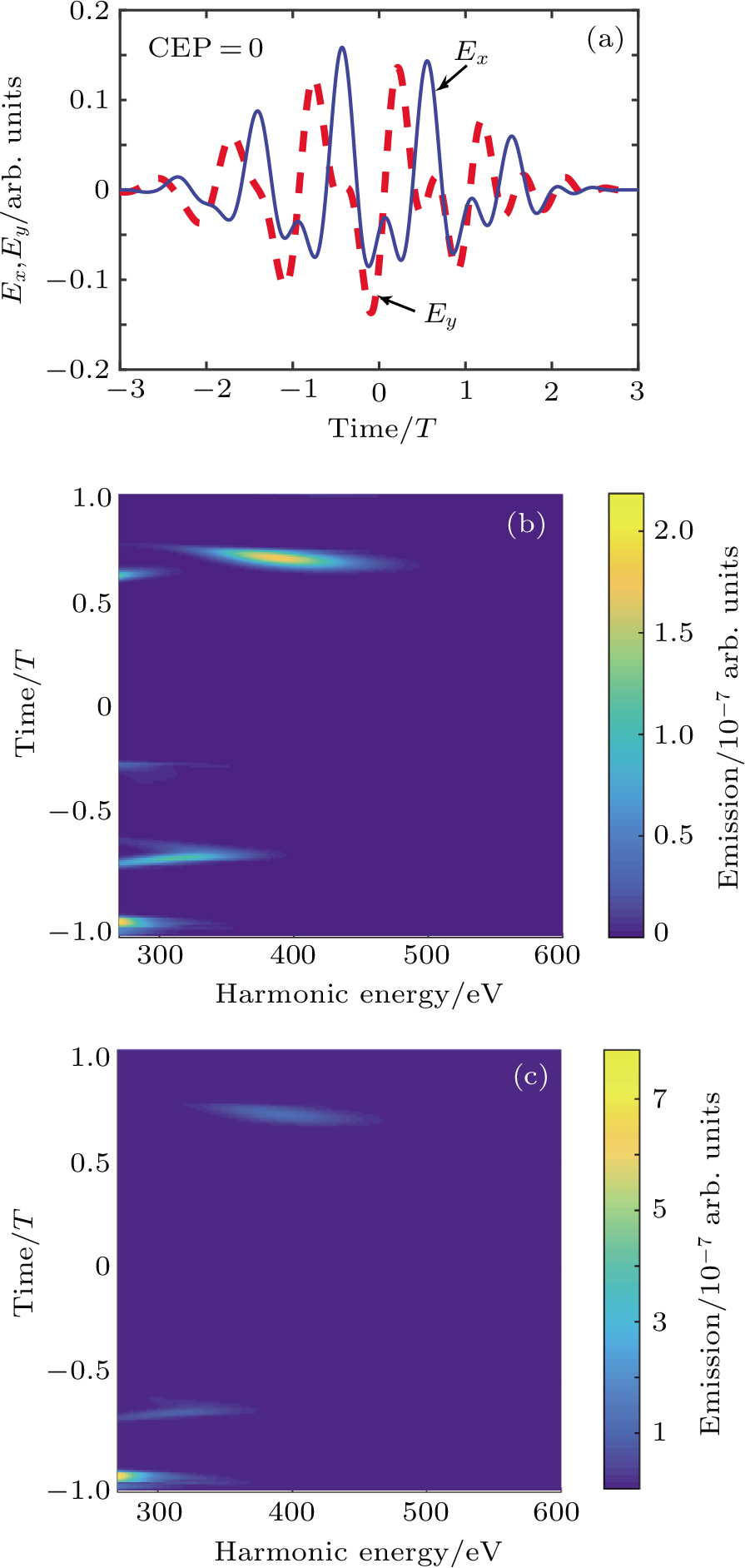
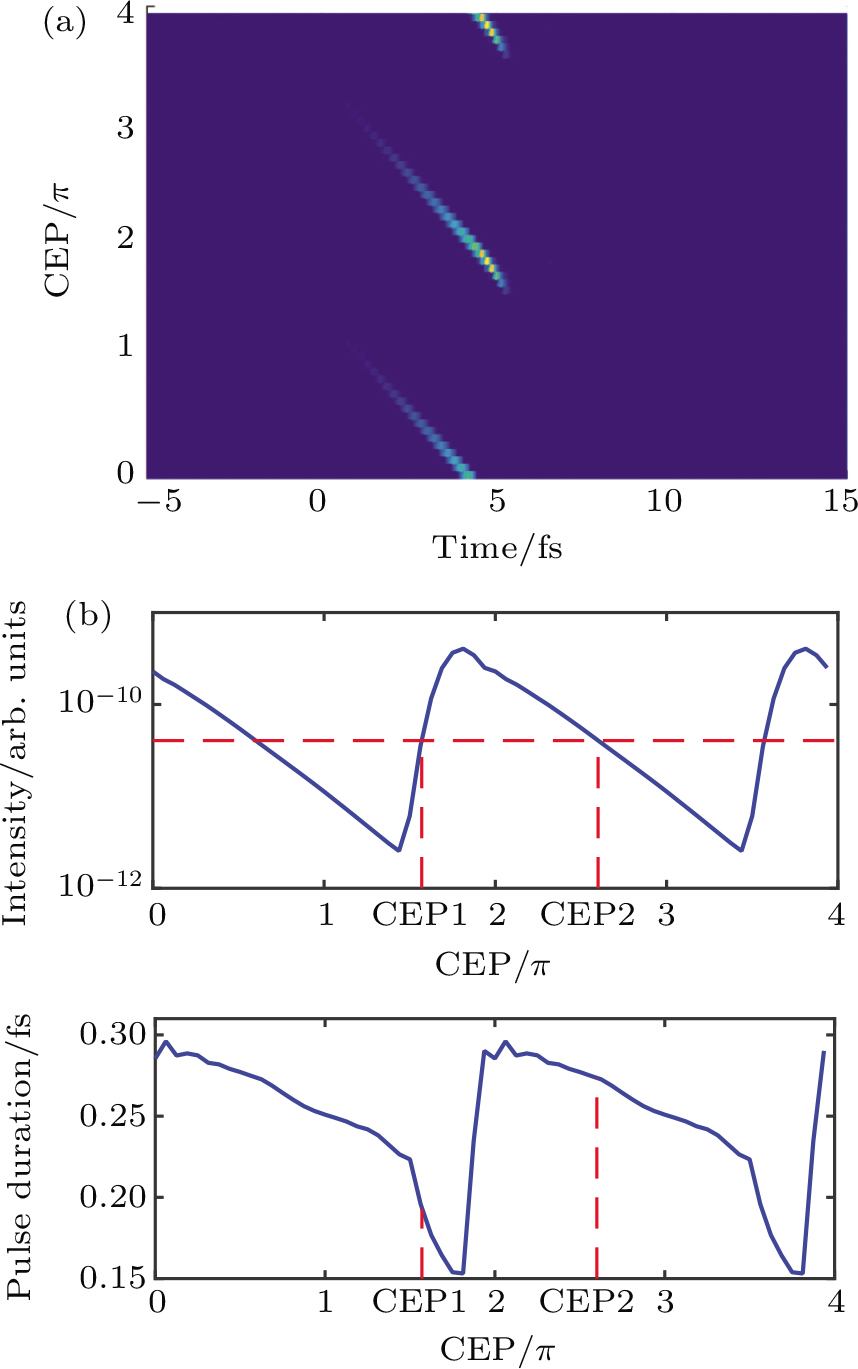Then we calculate the intensity and pulse duration of the generated IAP under different CEPs. The temporal intensity profile of the harmonic emission as a function of CEP is shown in Fig. 3(a). Double attosecond pulses are generated at some CEP, but their intensities are more than two orders of magnitude weaker than those of the intensest IAPs, as shown in the upper panel of Fig. 3(b). Therefore, IAPs are produced at most CEPs. The lower panel of Fig. 3(c) shows the relationship of the pulse duration of the generated IAP with CEP. The dashed lines in Fig. 3(b) indicate the variation of CEP when the intensity of IAP drops by one order of magnitude. We have CEP1 = 1.57π, CEP2 = 2.60π, ΔCEP = CEP2−CEP1 = 1.03π. The pulse duration varies between 153.1 as and 296.1 as in this CEP range. Compared with the former work,[27] the intensity of IAP varies more greatly, but this also means that almost no double attosecond pulses are generated.

Fig. 3. (color online) (a) Temporal intensity profile of the harmonic emission as a function of CEP. (b) Peak intensity (upper panel) and pulse duration (lower panel) of IAP as functions of CEP.

In this scheme, the electron motion is in two dimensions. Many electrons will not go back to their parent nuclei precisely. We perform the time-frequency analysis by means of wavelet transform of the induced dipole response of the helium atom to the laser fields[44,45] to investigate the electron emission characteristics, as shown in Fig. 4. Figure 4(a) shows the driving electric fields of orthogonal polarization. Figures 4(b) and 4(c) show the time-frequency distributions of the generated harmonic emission in the two directions x and y, respectively. The CEP of the two driving laser pulses is 0. The attosecond pulse is produced between 0.5 and 1 cycle. From these two figures, one can find that the attosecond pulse comes from the contribution of the long trajectory emission.

Fig. 4. (color online) (a) Electric fields of the driving laser along x-direction and y-direction. Time-frequency distributions for harmonic emission along (b) x-direction and (c) y-direction when CEP is 0.
4. Conclusion

We investigate the CEP effect of the few-cycle TC-CRCP laser pulses on the generation of IAP. We find that under specific delay of the two laser pulses, IAP can be generated at most of CEPs, although the intensity of the generated IAP varies with CEP. Double attosecond pulses can be seen at some CEPs, but they are negligible because their intensities are more than two orders of magnitude weaker than those of the intensest IAPs. The time-frequency analysis shows that the generated IAP comes from the electron of the long trajectory. As a result, the requirements for generation of IAP in experiments can be greatly reduced.

Reference
[1] Goulielmakis E Schultze M Hofstetter M Yakovlev V S Gagnon J Uiberacker M Aquila A L Gullikson E M Attwood D T Kienberger R Krausz F Kleineberg U 2008 Science 320 1614
[2] Sansone G Benedetti E Calegari F Vozzi C Avaldi L Flammini R Poletto L Villoresi P Altucci C Velotta R Stagira S Silvestri S D Nisoli M 2006 Science 314 443
[3] Zhao K Zhang Q Chini M Wu Y Wang X W Chang Z H 2012 Opt. Lett. 37 3891
[4] Agostini P DiMauro L F 2004 Rep. Prog. Phys. 67 813
[5] Lan P F Lu P X Cao W Wang X L Hong W Y 2007 Opt. Lett. 32 1186
[6] Du H C Luo L Y Wang X S Hu B 2012 Opt. Express 20 9713
[7] Cao X Jiang S C Yu C Wang Y H Bai L H Lu R F 2014 Opt. Express 22 26153
[8] Feng X M Gilbertson S Mashiko H Wang H Khan S D Chini M Wu Y Zhao K Chang Z H 2009 Phys. Rev. Lett. 103 183901
[9] Zeng Z N Cheng Y Song X H Li R X Xu Z Z 2007 Phys. Rev. Lett. 98 203901
[10] Lan P F Lu P X Cao W Li Y H Wang X L 2007 Phys. Rev. 76 011402
[11] Hong W Y Lu P X Lan P F Li Q G Zhang Q B Yang Z Y Wang X B 2008 Phys. Rev. 78 063407
[12] Miao J Zeng Z N Liu P Zheng Y H Li R X Xu Z Z Platonenko V T Strelkov V V 2012 Opt. Express 20 5196
[13] Xia C L Miao X Y 2015 Chin. Phys. Lett. 32 043202
[14] Du H C Wang H Q Hu B T 2010 Phys. Rev. 81 063813
[15] Zhao S F Zhou X X Li P C Chen Z J 2008 Phys. Rev. 78 063404
[16] Luo X Y Liu H F Ben S Liu X S 2016 Acta Phys. Sin. 65 123201 in Chinese
[17] Zhong S Y He X K Jiang Y J Teng H He P Liu Y Y Zhao K Wei Z Y 2016 Phys. Rev. 93 033854
[18] Mashiko H Gilbertson S Li C Q Khan S D Shakya M M Moon E Chang Z Z 2008 Phys. Rev. Lett. 100 103906
[19] Du H Zhang H D Zhang J Liu H F Pan X F Guo J Liu X S 2016 Chin. Phys. 25 113201
[20] Xue S Du H C Xia Y Hu B T 2015 Chin. Phys. 24 054210
[21] Zhong H Y Guo J Zhang H D Du H Liu X S 2015 Chin. Phys. 24 073202
[22] Zhang G T 2014 Chin. Phys. 23 043202
[23] Goulielmakis E Yakovlev V S Cavalieri A L Uiberacker M Pervak V Apolonski A Kienberger R Kleineberg U Krausz F 2007 Science 317 769
[24] Diao H H Zheng Y H Zhong Y Zeng Z N Ge X C Li C Li R X Xu Z Z 2014 Chin. Phys. 23 104210
[25] Zhang C M Wei P F Huang Y S Leng Y X Zheng Y H Zeng Z N Li R X Xu Z Z 2009 Opt. Lett. 34 2730
[26] Zhang C M Wang J L Wei P F Song L W Li C Kim C J Leng Y X 2009 Chin. Phys. 18 1469
[27] Zou P Zeng Z N Zheng Y H Lu Y Y Liu P Li R X Xu Z Z 2010 Phys. Rev. 82 053411
[28] Gilbertson S Khan S D Wu Y Chini M Chang Z H 2010 Phys. Rev. Lett. 105 093902
[29] Tong X M Chu S I 1998 Phys. Rev. 58 R2656
[30] Kfir O Grychtol P Turgut E Knut R Zusin D Popmintchev D Popmintchev T Nembach H Shaw J M Fleischer A Kapteyn H Murnane M Cohen O 2014 Nat. Photon. 9 99
[31] Mauger F Bandrauk A D Kamor A Uzer T Chandre C 2014 J. Phys. B-At. Mol. Opt. 47 041001
[32] Gilbertson S Mashiko H Li C Q Khan S D Shaya M M Moon E Chang Z H 2008 Appl. Phys. Lett. 92 071109
[33] Li L Wang Z Li F Long H 2017 Opt. Quant. Electron. 49 73
[34] Gu X Marcus G Deng Y P Metzger T Teisset C Ishii N Fuji T Baltuska A Butkus R Pervak V Ishizuki H Taira T Kobayashi T Kienberger R Krausz F 2009 Opt. Express 17 62
[35] Li C Wang D Song L W Liu J Liu P Xu C H Leng Y X Li R X Xu Z Z 2011 Opt. Express 19 6783
[36] Isaienko O Borguet E 2008 Opt. Express 16 3949
[37] Vozzi C Cirmi G Manzoni C Benedetti E Calegari F Sansone G Stagira S Svelto O Silvestri S D Nisoli M Cerullo G 2006 Opt. Express 14 10109
[38] Vozzi C Calegari F Benedetti E Gasilov S Sansone G Cerullo G Nisoli M Silvestri S D Stagira S 2007 Opt. Lett. 32 2957
[39] Gong C Jiang J M Li C Song L W Zeng Z N Miao J Ge X C Zheng Y H Li R X Xu Z Z 2012 Phys. Rev. 85 033410
[40] Wei P F Liu P Chen J Zeng Z N Guo X D Ge X C Li R X Xu Z Z 2009 Phys. Rev. 79 053814
[41] Takahashi E J Lan P F Mücke O D Nabekawa Y Midorikawa K 2013 Nat. Commun. 4 2691
[42] Jin C Wang G L Wei H Le A T Lin C D 2014 Nat. Commun. 5 4003
[43] Ishii N Kaneshima K Kitano K Kanai T Watanabe S Itatani J 2014 Nat. Commun. 5 3331
[44] Tong X M Chu S I 2000 Phys. Rev. 61 021802
[45] Carrera J J Tong X M Chu S I 2006 Phys. Rev. 74 023404