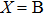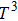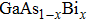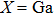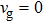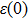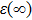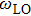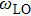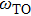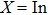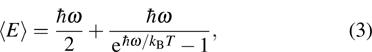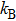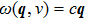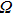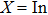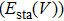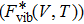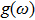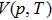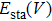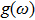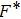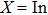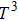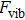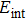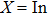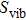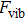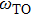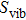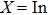Cite this Article
Shahri Raheleh Pilevar, Akhtar Arsalan. First principles study and comparison of vibrational and thermodynamic properties of X Bi (X = In, Ga, B, Al). Chinese Physics B, 2017, 26(9): 093107  
Permissions
First principles study and comparison of vibrational and thermodynamic properties of X Bi (X = In, Ga, B, Al)
Shahri Raheleh Pilevar †, Akhtar Arsalan
Department of Physics, Payame Noor University, Tehran, Iran

 

† Corresponding author. E-mail: ra_pilevar@yahoo.com

Abstract

In the present work, vibrational and thermodynamic properties of XBi (, Al, Ga, In) compounds are compared and investigated. The calculation is carried out using density functional theory (DFT) within the generalized gradient approximation (GGA) in a plane wave basis, with ultrasoft pseudopotentials. The lattice dynamical properties are calculated using density functional perturbation theory (DFPT) as implemented in Quantum ESPRESSO (QE) code. Thermodynamic properties involving phonon density of states (DOS) and specific heat at constant volume are investigated using quasi-harmonic approximation (QHA) package within QE. The phonon dispersion diagrams for InBi, GaBi, BBi, and AlBi indicate that there is no imaginary phonon frequency in the entire Brillouin zone, which proves the dynamical stability of these materials. BBi has the highest thermal conductivity and InBi has the lowest thermal conductivity. AlBi has the largest and GaBi has the smallest reststrahlen band which somehow suggests the polar property of XBi materials. The phonon gaps for InBi, GaBi, BBi and AlBi are about 160 cm−1, 150 cm−1, 300 cm−1, and 150 cm−1, respectively. For all compounds, the three acoustic modes near the gamma point have a linear behavior. CV is a function of at low temperatures while for higher temperatures it asymptotically tends to a constant as expected.

PACS: 31.15.es;63.20.dk;65.40.Ba;65.40.gd
Keyword:phonon dispersion;reststrahlen band;acoustic modes;optical modes specific heat
1. Introduction

The III–V semiconductors containing heavy bismuth (Bi) anion such as BBi, AlBi, GaBi, and InBi as well as their alloys have attracted technological interests in recent years due to applications in diode lasers, infrared photo-detectors and quadruple junction solar cells.[1–7] Most of the III–Bi compounds are expected to have a small energy gap, low ionicity, short bond length, high mechanical strength,[8–12] and high melting point.[13] Hence these materials are of great importance for numerous optoelectronic applications such as lasers, solar cells, transistors, and spintronic devices.[8,12,14–16] Bi is a key element for reduction of the band gap in GaAsBi and giant spin–orbit bowing.[5,17,18]

From experimental point of view, the III–Bi compounds are rarely studied. To our knowledge, only InBi and GaBi have been synthesized which of the latter has been incorporated in 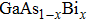alloys.[17,19–21] The lack of experimental data as well as their promising applications, have motivated theoretical scientists to explore structural, electronic, optical and mechanical properties of these compounds extensively during the past two decades.[8,14,16,22–24] Although considerable progress has been made in theoretical description of the structural and electronic background of these compounds and predicting new alloys,[22,25–28] many of their dynamical properties are still not well established and studies are in progress.Understanding the dynamical properties of these systems is important for characterization purposes and exploring their thermodynamic properties. Besides that, phonon dispersion diagram shows whether the structural phase is stable when no negative frequency is revealed. Hence detailed knowledge of the bulk phonon dispersion and thermodynamic properties of pure materials will be invaluable. Previous work has performed first-principles calculations of the structural and lattice-dynamical properties for the zinc-blend structure of BBi, AlBi, and GaBi while dynamical properties of InBi has not been considered.[23]

In this paper our aim is to briefly describe and compare these properties for XBi (, Ga, B, Al) compounds. First we calculate force constants for the materials which are used to compute the phonon dispersion and group velocity. Then by performing quasi-harmonic approximation, we investigate thermodynamic properties such as specific heat, entropy, free energy, and internal energy at the constant volume.

2. Methodologies

We have applied density functional theory (DFT) using the Perdew–Burke–Ernzerhof (PBE) parameterization of the generalized gradient approximation (GGA)[29] for the exchange–correlation functional and a plane-wave basis, with ultrasoft Vanderbilt pseudopotentials,[30] as implemented in Quantum ESPRESSO (QE) code.[31] The cutoff energy for the wave function and the charge density are chosen to be 40 and 400 Ry, respectively. The mesh sampling for Brillouin zone integrations is performed by 15 × 15 × 15 k-points mesh of Monkhorst and Pack.[32] The lattice dynamical properties are calculated using density functional perturbation theory (DFPT).[31] In particular, two dynamical matrices are calculated for 2 × 2 × 2 q-points mesh. These matrices are then Fourier interpolated to obtain the phonon dispersion curves. Thermodynamic properties involving phonon density of states (DOS) and specific heat at constant volume are investigated using quasi-harmonic approximation (QHA) package within QE.[33]

3. Results and discussion

XBi (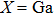, B, Al) compounds have zinc blend structure. Although InBi has a tetragonal structure experimentally,[19,20] here we studied its properties in assumed zinc blend structure for comparison purpose. To check the stability of these compounds in zinc blend structure, we first studied their dynamical stability by calculating the phonon spectra. Then thermodynamic properties are calculated. For the optimization, the force tolerance is Ry/Bohr on each atom and the maximum stress closes to zero within 0.5 kbar threshold. The relaxed lattice constants are obtained as 6.4407 Å, 5.5166 Å, and 6.4567 Å for AlBi, BBi, and GaBi respectively which are in agreement with the reported results in the Ref. [23] and 6.8382 Å for the zinc blend structure of InBi.

Before starting the analysis of vibrational properties for bulk XBi (, Ga, B, Al), we are going to discuss the general aspects of the phonon dispersions. Figure 1 represents the phonon dispersion diagrams for InBi, GaBi, BBi, and AlBi in high symmetry directions in Brillouin zone. The non-negative frequency of the phonon dispersions for all structures indicates that there is no imaginary phonon frequency in the entire Brillouin zone, which proves the dynamical stability of these materials. Considering two atoms in a primitive cell of these structures, there should exist six corresponding vibrational modes, in which three of them are acoustic and the others are optical modes. The interval between acoustic and optical branches where there is not any dispersion, is called phonon band gap. The gaps of InBi, GaBi, BBi, and AlBi are about 160 cm−1, 150 cm−1, 300 cm−1, and 150 cm−1, respectively. For all three acoustic modes near the gamma point, a linear behavior is observed for both longitudinal acoustic (LA) and transverse acoustic (TA) modes where TA mode has two-fold degeneracy in X– direction. Furthermore, the slope of the dispersion diagram gives the wave group velocity in the corresponding modes. The calculated TA and LA group velocities for each structure are plotted in Fig. 2.

Fig. 1. (color online) Phonon dispersion in high symmetric directions for (a) InBi, (b) GaBi, (c) BBi, and (d) AlBi.
Fig. 2. (color online) First derivative of phonon dispersion diagram (Fig. 1) in –X direction.

From Fig. 2 one can see that in point, the highest group velocity corresponds to LA mode of BBi and the lowest one corresponds to TA mode of InBi structure. Acoustic region dispersion with respect to q (in mathematical words indicates the sound speed and thermal conductivity of the material. Therefore, BBi has the highest and InBi has the lowest thermal conductivity in point. However, the values of the group velocity are not generally large and therefore the materials have got low thermal conductivity. Another point worth mentioning is that the slope of dispersion diagram at the edge of the first Brillouin zone (X) is zero (see Fig. 1) which leads to 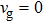. Consequently, there is not any transmission or thermal conductivity at the edge of the Brillouin zone.

In the presence of a transverse electric field, transverse optical (TO) phonons of a polar medium couple strongly to the electric field. When the wave vectors and frequencies of the external electric field and the transverse optical phonons are in resonance with each other, a coupled phonon–photon field is necessary to describe the system. The quantum of this coupled field is known as the polariton. We have

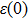
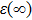
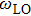
where and are static and high frequency dielectric functions, and and are LO and TO phonon modes frequencies, respectively. In the special case ω = 0 this relation reduces to the celebrated Lyddane–Sachs–Teller relationship[34]
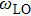
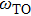
From phonon band diagram the calculated ratio of are 1.0325, 1.0221, 1.0213, and 1.0627 for InBi, GaBi, BBi, and AlBi, respectively, which are presented in Table 1. The gap between and is called reststrahlen band in which no electromagnetic wave can propagate in the medium. From Table 1, the existence of reststrahlen band for XBi materials suggests their polar property. AlBi has the largest and GaBi has the smallest reststrahlen band. Also it is obvious that the materials exhibit optical properties for far-infrared spectrum except a narrow gap in which the wave is reflected which is called restrahlen band.

Table 1.

Calculated Lyddane–Sachs–Teller relationship and reststrahlen band.

.

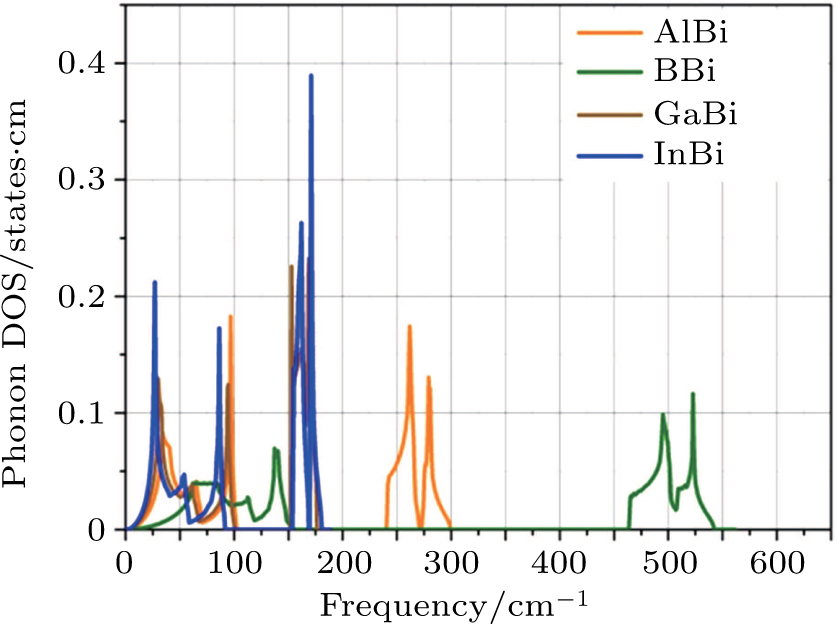
To compare the vibrational properties of these materials, we have calculated the total and projected DOS (PDOS) of phonon plotted in Fig. 3. Firstly from this diagram one can find out that mentioned vibrational band gaps are consistent with phonon dispersion diagrams. Secondly it is clear that the states for acoustic modes of all structures locate between 20 cm−1 to 100 cm−1 except BBi which reaches up to 150 cm−1. Moreover the optical modes spread over the interval of 225–300 cm−1 for AlBi, 465–550 cm−1 for BBi, and about 150–170 cm−1 for both InBi and GaBi. The smallest atomic mass of boron with respect to Al, Ga, and In is the main factor for the far spread of the optical frequencies of BBi. Figure 4 represents phonon PDOS for XBi (, Ga, B, Al). Almost in all structures only X atoms play role in optical modes whereas both X and Bi atoms have almost equal contributions in acoustic modes phonon DOS except for higher frequencies where Bi contribution is dominant.

Fig. 3. (color online) Total vibrational density of states for XBi (, Ga, B, Al).
Fig. 4. (color online) Projected density of states for (a) InBi, (b) GaBi, (c) BBi, and (d) AlBi.

To conclude our discussion, thermodynamic properties of XBi (, Ga, B, Al) have been calculated via QHA within QE code. QHA is a phonon based model to describe the volume-dependent thermal effects based on the assumption that the harmonic approximation holds for every value of the lattice constant. Thermal response of the material can be understood via thermal properties, so thermodynamic calculations of XBi (, Ga, B, Al) compounds are undeniably important because it is useful for the future experiments. Thus we attempt to investigate the thermal properties of XBi (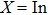, Ga, B, Al) compounds through the quasi-harmonic Debye (QHD) model. According to quantum statistical mechanics for an ensemble consisting of harmonic oscillators, Debye model describes the specific heat of solids at low temperature where the model assumes an assemblage of non-interacting quasi-particles such as phonons (lattice vibrations) which obey the Bose–Einstein statistics. In thermal equilibrium, a collection of harmonic oscillators with the angular frequency ω at temperature T has the internal energy of

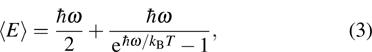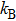
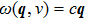
where is Boltzmann constant. At low temperatures, one could consider three degenerate modes in every Brillouin zone point, with the frequency of , where c is the sound velocity. The expression for the heat capacity, which is valid for low-temperatures would be found as
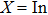
where and are the volume of the crystal’s unit cell and Debye temperature, respectively. As mentioned earlier to study the thermodynamic properties of XBi (, Ga, B, Al) we have applied QHA. For this purpose, non-equilibrium Helmholtz free energy ( will be the starting point of analysis as it follows
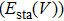
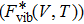
where it has two terms, namely, the crystal’s static energy for a given volume and the vibrational contribution . is expressed as
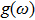
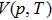
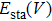
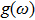
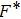
where it links to the lattice vibrations via the phonon density of states . Thus solving Eq. (6), desired thermodynamic properties are obtained using the equilibrium volume , the static energy and the phonon density of states . From thermodynamics we know that with the knowledge of , one can calculate a set of thermodynamic properties, such as the equilibrium entropy S, Helmholtz free energy F, internal energy U, and the constant-volume heat capacity CV, as
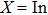
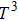
Using these equations, the curves of CV for XBi (, Ga, B, Al) are plotted in Fig. 5(a). At low temperatures, CV is a function of , and for higher temperatures it asymptotically tends to a constant. Finally, to study the thermal properties of matter, one has to exploit the entropy and free energy as a function of temperature. 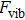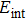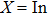The obtained results for temperature dependence of the entropy , free energy , and internal energy for XBi (, Ga, B, Al) are presented in Fig. 5(b) and Fig. 5(c), respectively. From Fig. 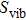5(b), we find that the calculated entropy gradually increases with increasing temperature which suggests that raising temperature causes the crystal plates to have more intense oscillations. 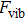Moreover, figure 5(c) depicts that as temperature increases the free energy gradually decreases and tends to zero and negative values while the internal energy increases.

Fig. 5. (color online) (a) Specific heat, (b) entropy , (c) free energy and internal energy at constant volume for XBi (, Ga, B, Al).
4. Conclusion

In the present work based on DFT, DFPT, and QHA study, vibrational and thermodynamic properties of XBi (, Ga, B, Al) are investigated. Phonon dispersion calculations have revealed that the zinc blende phases of BBi, AlBi, GaBi, and InB compounds are dynamically stable. BBi has the highest and InBi has the lowest thermal conductivity. The largest and the smallest reststrahlen bands are for AlBi and GaBi respectively which suggests the polar property of XBi materials. The vibrational gaps are about 160 cm−1, 150 cm−1, 300 cm−1, and 150 cm−1 for InBi, GaBi, BBi, and AlBi, respectively. The three acoustic modes near the gamma point have got a linear behavior. At low temperatures, CV is a function of , and for higher temperatures it asymptotically tends to a constant value as expected. Generally, these materials exhibit appealing optical properties that can be exploited for infrared and near infrared optoelectronic applications.

Reference
[1] Ma K Y Fang Z M Cohen R M Stringfellow G B 1992 J. Electron. Mater. 21 143
[2] Oe K Okamoto H 1998 Jpn J. Appl. Phys. 37 L1283
[3] Oszwaldowski M Berus T Szade J Jozwiak K Olejnikzak I Konarski P 2001 Cryst. Res. Technol. 36 1155
[4] Oe K 2002 Jpn J. Appl. Phys. 41 2801
[5] Francoeur S Seong M J Mascarenhas A Tixier S Adamcyk M Tiedje T 2003 Appl. Phys. Lett. 82 3874
[6] Tixier S Adamcyk M Tiedje T Francoeur S Mascarenhas A Wei P Schiettekatte F 2003 Appl. Phys. Lett. 82 2245
[7] Vaddiraju S Sunkara M K Chin A H Ning C Z Dholakia G R Meyyappan 2007 J. Phys. Chem. 111 7339
[8] Wang S Ye H 2002 Phys. Rev. 66 235111
[9] Janotti A Wei S H Zhang S 2002 Phys. Rev. 65 115203
[10] Knittle E Wentzcovitch R M Jeanloz R Cohen M L 1989 Nature 337 349
[11] Garcia A Cohen M L 1993 Phys. Rev. B 47 4215
[12] Wentzcovitch R M Cohen M L Lam P K 1987 Phys. Rev. 36 6058
[13] Wettling W Windscheif J 1984 Solid State Commun. 50 33
[14] Zhang Y Mascarenhas A Wang L W 2005 Phys. Rev. 71 155201
[15] Madouri D Ferhat M 2005 Phys. Status Solidi 242 285
[16] Ferhat M Zaoui A 2006 Phys. Rev. 73 115107
[17] Fluegel B Francoeur S Mascarenhas A Tixier S Young E C Tiedje T 2006 Phys. Rev. Lett. 97 067205
[18] Madouri D Boukra A Zaoui A Ferhat M 2008 Comp. Mater Sci. 43 818
[19] Jorgensen J D Clark J B 1980 Phys. Rev. 22 6149
[20] Degtyareva V F Winzenick M Holzapfel W B 1998 Phys. Rev. 57 4975
[21] Francoeur S Seong M J Mascarenhas A Tixier S Adamcyk M Tiedje T 2003 Appl. Phys. Lett. 82 3874
[22] Amrani B Achour H Louhibi S Tebboune A Sekkal N 2008 Solid State Commun. 148 59
[23] Belabbes A Zaoui A Ferhat M 2008 J. Phys. -Condens. Mat. 20 415221
[24] Rahim N A A Ahmed R Haq B U Mohamad M Shaari A Ali N Goumri-Said S 2016 Comp. Mater. Sci. 114 40
[25] Cang Y P Lian S B Yang H M Chen D 2016 Chin. Phys. Lett. 33 066301
[26] Wu J H Liu C X 2016 Chin. Phys. Lett. 33 036202
[27] Feng S Q Li J Y Cheng X L 2015 Chin. Phys. Lett. 32 036301
[28] Wang J F Fu X N Zhang X D Wang J T Li X D Jiang Z Y 2016 Chin. Phys. 25 086302
[29] Hohenberg P Kohn W 1964 Phys. Rev. 136 864
[30] Vanderbilt D 1985 Phys. Rev. 32 8412
[31] Baroni S de Gironcoli S Dal Corso A Giannozzi P 2001 Rev. Mod. Phys. 73 515
[32] Monkhorst H J Park J D 1976 Phys. Rev. 13 5188
[33] Baroni S 2011 EPJ Web of Conferences 14 02001
[34] Lyddane R H Sachs R G Teller E 1941 Phys. Rev. 59 673