Cite this Article
Bai Li-Na, Liu Hai-Dong, Zhou Wei, Zhang Yong, Zhai Hong-Qi, Cui Zhen-Jian, Zhao Ming-Ying, Gu Xiao-Qian, Liu Bei-Ling, Huang Li-Bei. ADC border effect and suppression of quantization error in the digital dynamic measurement. Chinese Physics B, 2017, 26(9): 090601  
Permissions
ADC border effect and suppression of quantization error in the digital dynamic measurement
Bai Li-Na1, †, Liu Hai-Dong1, Zhou Wei1, Zhang Yong2, Zhai Hong-Qi1, Cui Zhen-Jian1, Zhao Ming-Ying1, Gu Xiao-Qian1, Liu Bei-Ling1, Huang Li-Bei1
Department of Measurement and Instrumentation, Xidian University, Xi’an 710071, China
State Key Laboratory of Electrical Insulation and Power Equipment, Xi’an Jiaotong University, Xi’an 710049, China

 

† Corresponding author. E-mail: lnbai@mail.xidian.edu.cn

Abstract

The digital measurement and processing is an important direction in the measurement and control field. The quantization error widely existing in the digital processing is always the decisive factor that restricts the development and applications of the digital technology. In this paper, we find that the stability of the digital quantization system is obviously better than the quantization resolution. The application of a border effect in the digital quantization can greatly improve the accuracy of digital processing. Its effective precision has nothing to do with the number of quantization bits, which is only related to the stability of the quantization system. The high precision measurement results obtained in the low level quantization system with high sampling rate have an important application value for the progress in the digital measurement and processing field.

PACS: 06.20.Dk;07.50.Qx
Keyword:quantization error;border effect;digital converter (ADC)
1. Introduction

In the digital age,[1] improving the digital measurement accuracy is the goal that all fields have been pursuing. At present, an important development trend is to reduce the quantization error and improve the measurement accuracy by improving the quantization bits.[2–11] But when the figure of the digital conversion improves, the sampling rate would be reduced. For a 24 bit quantized digital system, the sampling rate is only a million samples per second (MSPS), while an 8 bit quantized digital system has a sampling rate up to a gigabit samples per second (GSPS). The concept, application, and development of the border effect[12,13] can make the low bit quantization system realize the measurement accuracy that is higher than the quantization resolution. Meanwhile, for the less quantization bits, the quantization system could reach a higher sampling rate.[14] Based on this, in this paper we will discuss how to apply the border effect theory to the measurement of the multi-fuzzy zone border in digital measurement.[5,15] The border effect theory is verified by the measurement of the AC voltage. In the actual quantified measurement, we can make the corresponding fitting[16] according to the characteristics of the physical quantity. Compared with the traditional analog to digital converter (ADC), extracting the effective information[17–21] using the border effect in the digital quantization could obtain higher precision. As a breakthrough progress in the measurement field, the border effect is widely applied to some simple physical quantity measurements where we can obtain better measurement results. It has also been fully applied in the precision frequency measurement[21–23] and has some advantages over the conventional methods. If there is no detailed analysis of the border effect principle, it is very difficult to understand and apply in some complicated situations, such as the discrete fuzzy zone, the concentrated fuzzy zone, and the dynamic multi-fuzzy zone of the digital quantization process.

The essence of the border effect is that in the numeral mode conversion process, the border value of the measurement fuzzy zone between two adjacent quantizations is more stable[24–30] and then we can obtain higher precision than traditional quantization through selecting these values of the jump edge. The viewpoint of this technology aims to be widely applied for various fields using digital quantization, such as digital sensing measuring instruments, communication, navigation, positioning, and so on,[23] that is, high precision measurement could be obtained by using the stability of dynamic edge information in the multi-fuzzy zones. The same approach that improves the measurement resolution and accuracy using the border effect could also be applied for the linear varying voltage,[31–35] such as the linear degree measurement of triangular wave and saw tooth wave voltages and the precision measurement of the linear phase comparator.[35] It can also be used for the detection and calibration of the input–output characteristics of the sensor. At the same time, this method is more suitable for the measurement of the dynamic characteristics of the fast changing signals, such as the rising edge of the pulse signal, the rate of change of the slope, the linearity of the signal change, and so on. In the processing of these problems, the conventional sampling number and sampling rate are contradictory, while the approach could make the low-bit ADC[36] with high conversion rate obtain high precision measurement. This will provide a better measurement method for measuring the dynamic multi-fuzzy zone formed by the limited resolution of the measure object,[11] improving the accuracy in the measurement and control. This will also open up a new way for the development of high precision digital measurement, and promote the development of various fields to a higher level.

2. Method
2.1. Dynamic fuzzy zone and quantization stability in the digital quantization

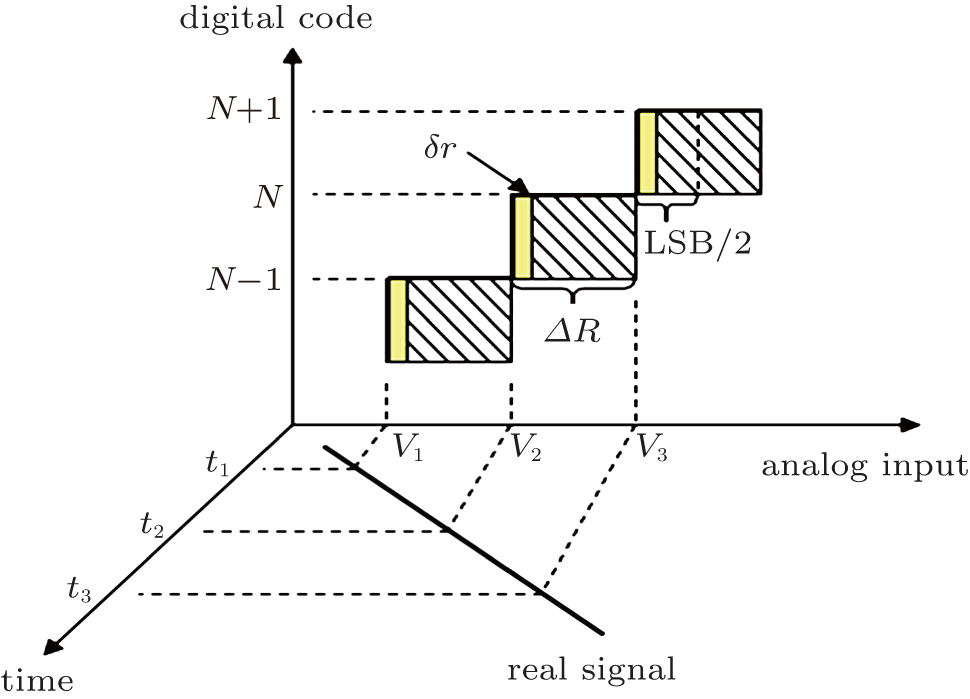
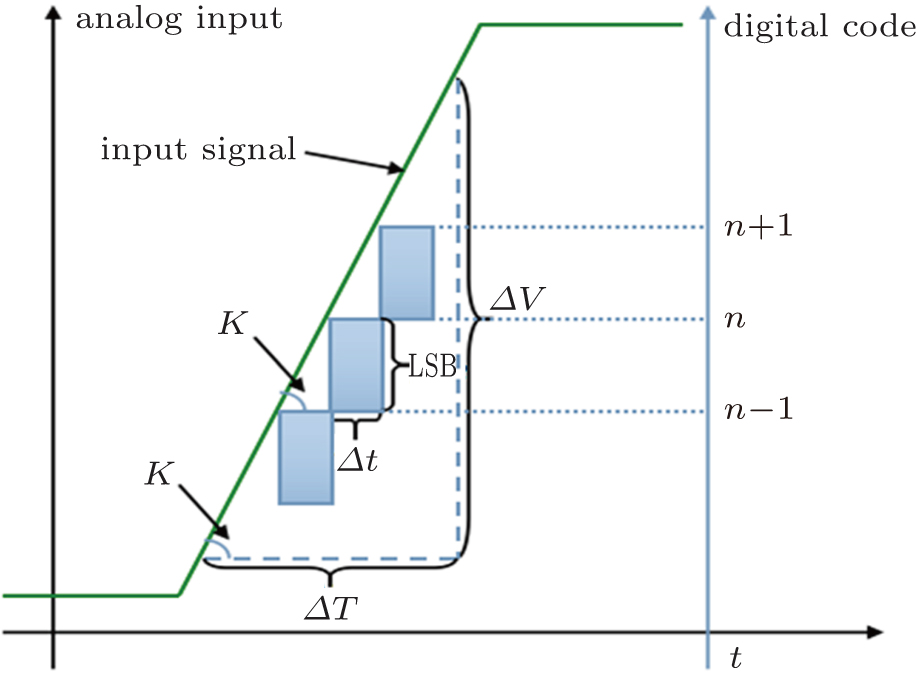
The multi-fuzzy zone is a unique property of the digital quantization system, and the border of the fuzzy zone has a very high stability too. Systematic analysis and experiment validation of the quantitative edge show that higher resolution than the device’s measuring precision can be obtained by processing data at the dynamic fuzzy zone border. On the analysis of the fuzzy zone, through the periodic signal frequency stability in the measurement,[37–40] precision is improved significantly. On this basis, higher accuracy than the quantitative value can be obtained by correcting and fitting values at the dynamic multi-fuzzy zones. A digital quantitative dynamic fuzzy zone diagram is shown in Fig. 1. It shows the quantitative process of the actual signal, which forms a continuous signal to a continuous ladder-like fuzzy zone. When the input signal comes to the quantitative edge, the digital result changes and has the minimum difference with the input signal in this location.

Fig. 1. Dynamic fuzzy zone of ADC.

For a practical digital quantitative system, the quantitative resolution (dynamic fuzzy zone size) is

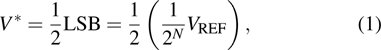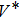
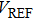
where is the maximum error of measurement, N is the quantitative bit, and is the reference voltage.

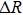
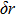
Assume that is the quantitative resolution, namely, the quantitative fuzzy zone, and is the stability of the fuzzy zone border. The amplification coefficient A is given as

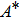
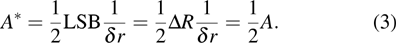In Fig. 1, half of the fuzzy zone is 1/2 LSB of quantitation, and in the process of digital quantitation, the improvement of the actual measurement precision is

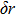
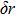
The stability of resolution on the border is , and is related to temperature T, noise S, and the conversion principle C. So when the environmental temperature change is very small, and the noise of the circuit itself is very weak at the same time,[41] the stability at the border will be very high

The actual measurement error is

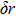
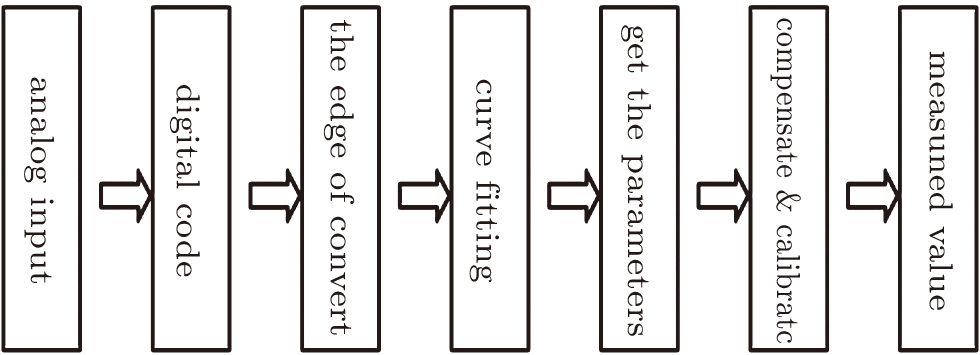
According to Eq. (5), when the physical entity of a digital quantitative system has been confirmed, the highest measurement resolution can be reached under the border effect only related to . The conversion principle C of the converter will be different, but once the device is determined, it is only related to temperature T and noise S, the quantization error determined by the measurement error can be eliminated. So the actual accuracy measured is significantly superior to one of the system itself. When processing data, the fuzzy zone can be formed at quantitative borders. Cause data at borders have stable and high precision characteristics, and the stable characteristics will remain, correcting and processing the data effectively can result in a higher precision.

2.2. Application of the border effect in data sampling and waveform restoration

The data processing applying the border effect is shown in Fig. 2, which is of strong representation and can be involved in any digital quantization system.

Fig. 2. Data acquisition and processing of border effect.

According to the sample rate and quantitative value, we can obtain the two-dimensional information of the input signal at quantitative edge. Then, we can fit the correction of the input signal using these values and rebuild the input signal to the greatest extent. Meanwhile, the process automatically fits the optimization point, and further reduces the random noise caused by the edge jitter. On this basis, according to the demand, the waveform parameters will be measured, which will be more convenient and quick. Finally, we can obtain a more accurate result than traditional direct measurement with compensation and correction. If the measured signal is a nonsinusoidal signal or a signal with distorted waveform, the measurement for the valid value will no longer apply to the principle “the corresponding relationship between the effective value and amplitude of the standard sine signal” described in this paper. Fitting the measured signal according to the sampling point and calculating the valid value by integral operation on the basis of the definition of valid value, the higher precision measurement results can still be obtained compared with the traditional measurement scheme. This is a more advanced processing method. The measurement method in this paper is only used as an example to explain the principle of the program. In Fig. 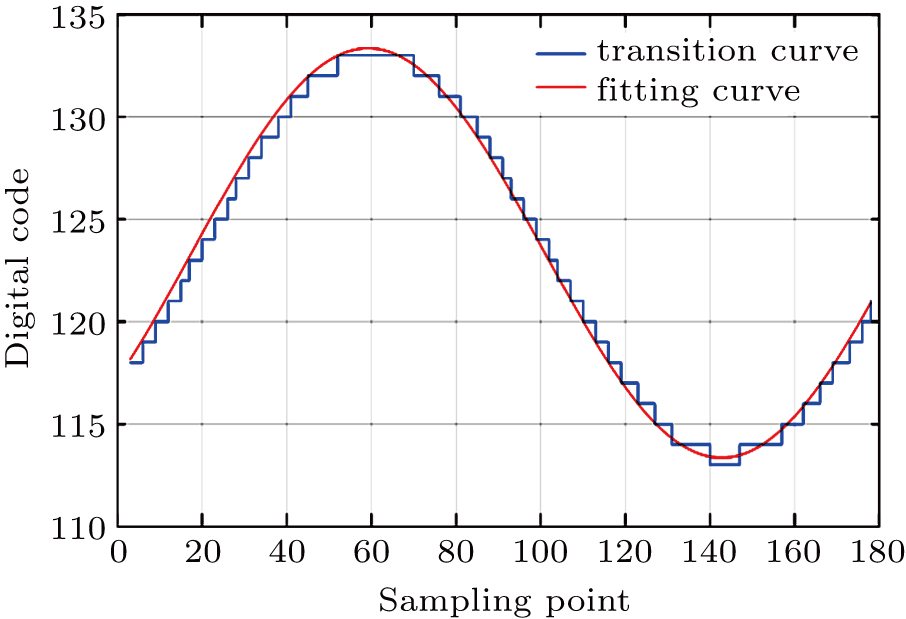3, according to the digital value of ADC, the sampling results will include more error at the top and bottom points of the input signal, which will cause the loss of the amplitude information, because the quantitative value is an integer. Based on the border effect to fit the cure, we can restore the true amplitude information of the signal. At this time, the real quantitative value is equal to the practical quantitative value plus a small value which is less than one quantitative. That is to say, the eliminating top of the waveform has been compensation.

Fig. 3. The dynamic fitting curve.

In order to improve the measurement accuracy, the traditional digital method makes use of the average of many different collecting results. Because of different sampling points with different measuring accuracy, the method has a great disadvantage. Only some minority points at the quantitative edge are of high accuracy. However, most sampling points deviate from the edge with huge error. The data processing on the basis of these points is limited to their accuracy, so it is very difficult to improve the measuring accuracy significantly. The sampling value of points at the quantitative edge can be achieved effectively, namely, the border effect, and the border can be obtained by use of the AC voltage signal quantization. Taking advantage of the border effect, a higher accuracy may be realized, owing to the high accuracy of the edge points. In the actual experiments, a standard sine signal source is used as the measured signal which is sampled and processed by applying the border effect. The phenomenon of quantitative edge would be more obviously, especially at the peaks and troughs. The obtained border quantization value is used to fit a sine wave, meanwhile, part of points deviating from the fitting curve can be automatically removed by the system device. Therefore, the measurement error could be reduced greatly and it also means the higher measurement accuracy.

3. Results
3.1. Amplitude characteristic

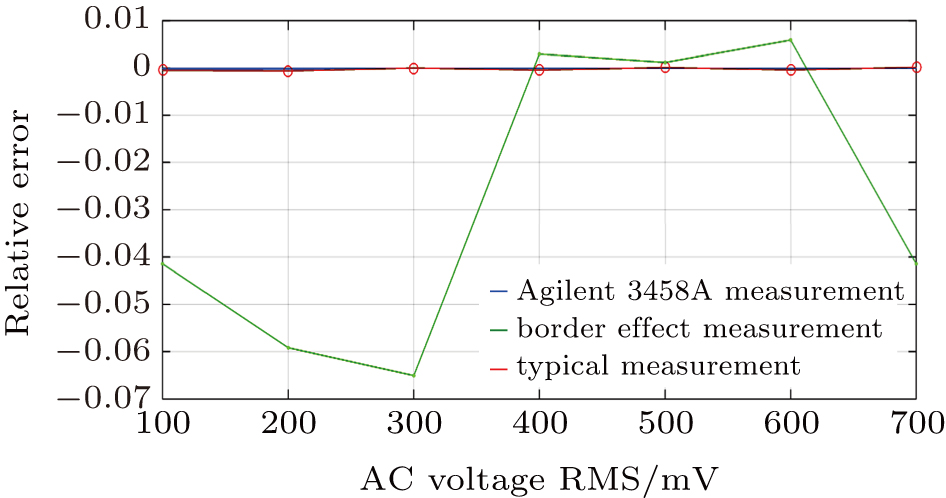
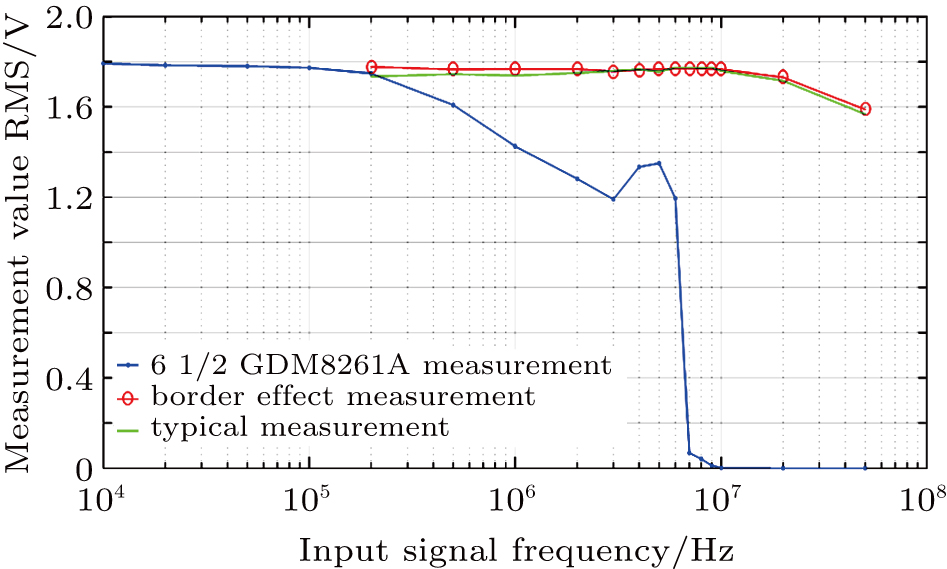
The measurement accuracy can be improved greatly by applying the border effect. Whether it is a centralized fuzzy zone, a discrete fuzzy zone, or a dynamic progressive multi-fuzzy zone, the quantitative fuzzy zone exists when it has the quantization. And its essence is that the edge of the fuzzy zone produced in the adjacent digital conversion is more stable than that in the whole fuzzy zone, and the edge position of the fuzzy zone reflects the stability[12,13] of the fuzzy zone. Therefore, the edge value could be obtained effectively based on the principle of the border effect. Because the edge value has a higher precision than the quantization value and its accuracy is only related to the border stability of the fuzzy zone, the collected points are high precision points. Based on the process of data processing, this method has higher measurement accuracy than the conventional method. In order to verify the measurement results applying the principle of the border effect of the dynamic multi-fuzzy zone, we adopt the signal source (Fluke5520) whose measurement error is up to 1/10000 to 1/100000 as the output signal of the system device. The experiment results are compared among three measurement methods, they are the 8 bit ADC using the border effect, the direct measurement devices, and the high-precision Agilent3458A. The result of relative error of the three methods is shown in Fig. 4. Using the basis of the principle of the dynamic fuzzy zone of the multiple border effect has a significant advantage over the ADC in a traditional direct way in measurement. Compared with the advanced high precision measuring equipment (Agilent3458A), they have similar error.

Fig. 4. Amplitude characteristic relative error curve.
3.2. Frequency characteristics

The measurement results based on the border effect have better amplitude and frequency characteristics. The measurement of the effective value of the AC voltage is used to verify the border effect of the dynamic multi-fuzzy zone. In the actual measurement, most signals are varied, for example, the AC signal. Yet the constant DC signal is only a special case. Therefore, the measurement of the AC voltage can widely represent the applications of many digital quantization measurements at the present stage[42,43] and reveal that the quantization resolution of the system devices is fixed, the measurement accuracy is greatly improved when the multi-fuzzy zone border information is obtained using the quantization stability of the system.[12,13] Comparing the 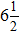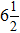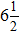digital multimeter GDM8261A (equal to 21bits) with 8 bit ADC direct measurement, the results are shown in Fig. 5. We can see that the multimeter has very high measurement accuracy below the range 100 kHz. But when the frequency is up to several hundred kHz, the measurement error would increase rapidly owing to the limit of the measurement principle. While for the 8 bit ADC measurements based on the border effect, we can find that the frequency range is obviously higher than that that of the multimeter.

Fig. 5. The frequency characteristic curve.

The experimental results of the two groups are consistent using the 8 bit ADC. Although the results of direct measurement have good high frequency characteristics, the amplitude characteristics have large errors.

The experiment indicates that the digital measurement applying the border effect principle could make the measurement accuracy immune from the quantization bits, and verifies that the border effect principle can be used to realize more higher measurement resolution when measured in a dynamic state. From the frequency characteristics, the method is equal to the conventional ADC sampling. The measurement upper limit of the AC voltage effective value is obviously higher than that of the traditional rectifier filter mode,[42–46] and its frequency measurement upper limit depends on the highest sampling rate of ADC.[46–49] From the precision characteristics, the maximum measurement error of the 8 bit ADC adopting the conventional measurement scheme depends on the maximum quantization error. The measurement accuracy of the single point can be greatly improved when it adopts the idea of transforming edge value fitting. According to the existing experimental results, the measurement accuracy can be increased by nearly 100 times under a certain noise background. For multiple point measurement, because the fitting point has a high precision, the fitting result also has a high precision.

3.3. Measurement of transient parameter about fast changing signal

Figure 6 shows the applications of the pulse response time, fast changing signal slope, and its transient response. The input signal is a rising step, and its slope can be said to have angle K. The picture shows the process of the digital quantitative.

Fig. 6. Fast rising signal parameter measurement.

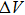
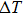
In order to obtain the change of the rise time or slope, we measure the change of the signal amplitude during a period of time , and calculate its slope K as follows:

Measured by the digital device, the method could be reduced in proportion, until the voltage we are concerned with transforms the minimum voltage resolution of the converter, that is quantization error LSB, while the time interval transforms the sampling interval 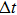of the converter. Next we derive the maximum range of signal slope variation measured by the ADC.

The large time interval and the voltage variation are reduced to the minimum quantization level and the sampling rate of the converter, the slope K can be expressed as

While the relationship between the sampling rate S and the minimum sampling time of the ADC is
So the slope is
and

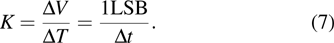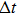
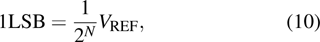It can be seen from the above equations that the measurable slope range is related to the number of quantization bits N, the reference voltage 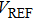, and the sampling rate S. The realization of the maximum measurement slope variation requires increasing the sampling rate, small quantization bits, and improving the reference voltage level. Only low-bit ADC meets the top two items. The low-bit converters applying the border effect principle can improve greatly the measurement accuracy, meanwhile, its conversion speed would not reduce. Therefore, it is the only choice to measure the rapid change of the signal, as well as the pulse measurement.

3.4. Actual measurement accuracy

The highest accuracy which the digital system can realize depends on its stability. In our original work, the verified experiments were mainly aimed at periodic signals.[43] The structure of the fuzzy zone was relatively simple, meanwhile, the possible range of its application was not also very wide. The experiment of dynamic multi-fuzzy zones can illustrate that the measurement accuracy of the measuring device depends on its stability index under complicated circumstances. Therefore, it is the optimal selection for the dynamic digital measurement to choose the high speed and low-bit ADC instead of the low speed and high-bit ADC. This will provide a very important reference for the future development and application of ADC devices.

The actual measurement accuracy of the digital quantization system depends on the sampling rate. The border effect is used to improve the measurement resolution in dynamic digit measurement. Its theoretical basis is that the conversion edge value of the quantization system has significantly higher stability and accuracy than the other locations. So if we would use the principle in practical applications, we must find the exact location of the conversion edge value. The accuracy of its value determines the accuracy that the system can reach.

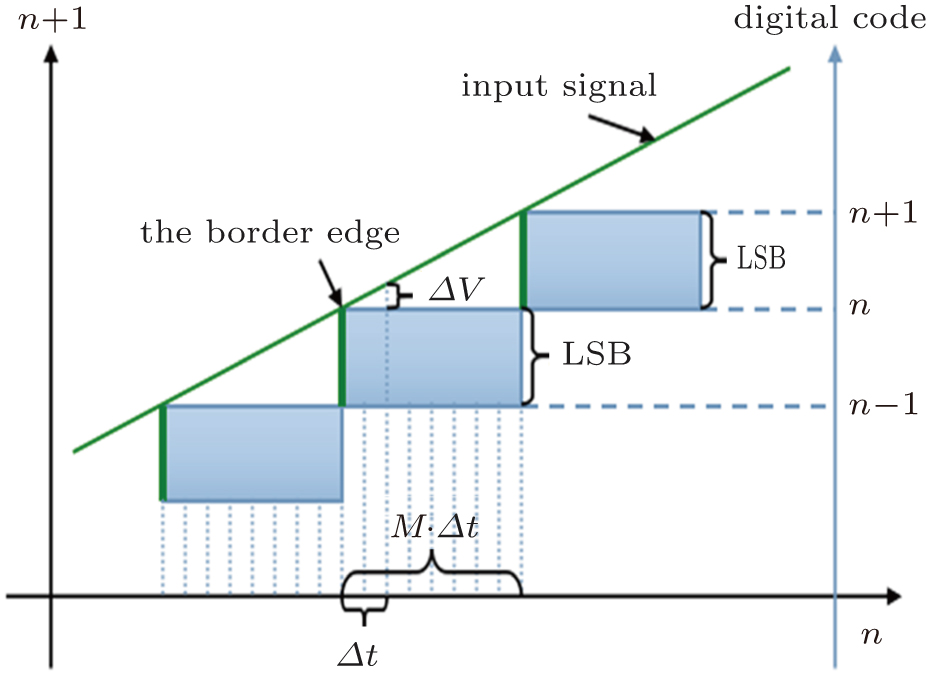
According to Fig. 7, ADC has a minimal error of 1/2 LSB in traditional function. We increase the sample rate in the timeline that every quantitative fuzzy zone can include more sample points (the point in the timeline of the picture), and the precise location of the quantitative edge is depending on the interval of sample points. For a practical digital system, the finite sampling rate results in that the sample point cannot be infinitely close to the quantitative edge, and the quantitative edge randomly changes with the input signal, both result in the quantitative edge inaccuracy.

Fig. 7. (color online) The relationship between actual resolution and sampling rate.

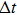
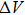
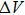
When improving the sampling rate, the quantization error LSB of a quantization system causes that there are M sampling values between the adjacent quantitative fuzzy zones. At this moment, the maximum error of the true position of the conversion edge is the same as the maximum error on the vertical axis and also the same as M subdivision on the fuzzy zone. Therefore, the measurement error applying the border effect is

Here M is equivalent to the subdivision factor, and M is inversely proportional to according to Eq. (8), so
That is, the formula can obtain the resolution by the border effect. The measurement accuracy can be improved through increasing the sampling rate when the quantization system is fixed. The application of the border effect is a new implementation method for the high-precision digitized measurement.

It can also be seen from the chart that improving the accuracy using the border effect depends on the stability at the conversion edge; it is shown as the subdivision of the time axis. It means that the subdivision of the voltage on the vertical axis would be converted to the temporal subdivision. The biggest characteristic of the low-bit ADC is that they have a very high sampling rate, which means that the low-bit ADC as usual could achieve a high precision result by the border effect.

4. Summary and discussion

By using this method based on the border effect, the border information of a dynamic fuzzy zone can be captured. Therefore, we abandon the traditional data processing method, which needs times of sampling and averaging to reduce the quantization error. We collect data selectively, and find the border location and convert data. For the quantitative system, the quantization edge value has higher sensitivity compared to the quantization resolution, and small changes of input will cause the change of the quantitative results, and the difference between real values is minimal.[12,13,44–47] So the precision of the points on the borders is significantly higher than that in other zones. Better results can be obtained by processing the higher precision points. Due to the use of low converters, the actual sampling rate can be very high. Based on the idea of the border effect, high-precision measurement can be realized and higher frequency range can be obtained at the same time.

In digital quantitation, research and application on borders of the dynamic fuzzy zone are based on single side stability. In a broad sense, it is a quantitative system of physical properties for the quantitative of extreme stability, and it is also a unique property which is often ignored in digital quantitative systems. Therefore, a further study of its characteristics is the key technology of the border effect. In the digital quantitative system, the linearity of quantitative borders also needs to be focused on. Because ADC has the biggest nonlinear error related to the effective quantitative bit,[44–47] and its value is at the minimum quantitative level, which leads to a non-uniformity between multiple quantitative borders in the whole quantitative range. The points at border locations will change due to the non-uniformity. The deviation value is significantly bigger than the stability of the quantitative border. Actually, ADC products will make the error below 1/2 LSB. In applications, the error of measuring results in the biggest impact, therefore, we need to calibrate all quantitative borders in ADC to make sure of the high precision of the measurement results.[50] In experiments, inevitably noise of the circuit itself and additive noise[51] will be added to the measured results, which leads to a small jitter in the actual conversion border and it has higher instability than the actual stability. So the quantitative random deviation of the border value should be taken into account in data processing and by selecting subsequent values at the borders, we can get rid of the interference of random noise[47–49] to make it closer to the border of its true position. According to our experiments, under certain outside noise background, compared to the direct measurement by ADC, the accuracy of the measurement results applying the border effect principle could be improved nearly 100 times. This effect exists universally.

Reference
[1] Diddams S A Bergquist J C Jefferts S R Oates C W 2004 Science 306 1318
[2] Barber Z W Babbitt W R Kaylor B Reibel R R Roos P A 2010 Appl. Opt. 49 213
[3] Eramo R Cavalieri S Corsi C Liontos I Bellini M 2011 Phys. Rev. Lett. 106 213003
[4] Sturm S Kohler F Zatorski J Wagner A Harman Z 2014 Nature 506 467
[5] Resch K J Pregnell K L Prevedel R Gilchrist A Pryde G J O’Brien J L White A G 2007 Phys. Rev. Lett. 98 223601
[6] David J Starling P Ben D Andrew N J John C H 2010 Phys. Rev. 82 063822
[7] Budovsky I Hammond G 2005 IEEE Trans. Instrum. Meas. 54 483
[8] Wang B Gao C Chen W L Miao J Zhu X 2012 Sci. Rep. 2 556
[9] Archanaa M Balamurugan K Jayakumar M 2014 International Conference on Embedded Systems (ICES) July 3–5, 2014 Coimbatore, India 39 10.1109/EmbeddedSys.2014.6953047
[10] Li Z Q Zhou W Zhou H Zhang X P Zhao J 2013 Rev. Sci. Inst. 84 025106
[11] Giorgetta F R Coddington I B E Swann W C Newbury N R 2010 Nat. Photon. 4 853
[12] Zhou W Li Z Q Bai L N 2014 Chin. Phys. Lett. 31 100602
[13] Bai L N Su X Zhou W Ou X J 2015 Rev. Sci. Inst. 86 015106
[14] Rapp P E Cellucci C J Korslund K E Watanabe T A A Jiménez-Montaño M A 2001 Phys. Rev. 64 016209
[15] Shan H T Chen X K Kong X J Zhang Y Liu Z Li H B Li T F 2009 IEEE 6th International Power Electronics and Motion Control Conference May 17–20, 2009 Wuhan, China 1554 10.1109/IPEMC.2009.5157636
[16] Pumplin J Stump D R Tung W K 2001 Phys. Rev. 65 014011
[17] Kurten-Ihlenfeld W G Landim R P 2014 29th Conference on Precision Electromagnetic Measurements (CPEM) August 24–29, 2014 Rio de Janeiro, Brazil 766 10.1109/CPEM.2014.6898611
[18] Lin H B Lv X L 2010 International Conference on Electrical and Control Engineering June 25–27, 2010 Wuhan, China 2315 10.1109/iCECE.2010.570
[19] An G C Sha Z Y 2007 8th International Conference on Electronic Measurement and Instruments August 16–18, 2007 Xi’an, China 1 453 10.1109/ICEMI.2007.4350484
[20] Roulleau P Portier F Roche P Cavanna A Faini G Gennser U Mailly D 2008 Phys. Rev. Lett. 100 126802
[21] Udem T Holzwarth R Hansch T W 2002 Nature 416 233
[22] Vanier J 2002 Phys. Today 93 522
[23] Schröder G F Levitt M Brunger A T 2010 Nature 464 1218
[24] Jaseja T S Javan A Townes C H 1963 Phys. Rev. Lett. 10 165
[25] Zheng H X Dougal R A Ali M H 2013 Electric Ship Technologies Symposium (ESTS) April 22-24, 2013 Arlington, VA, USA 292 10.1109/ESTS.2013.6523749
[26] Antonio D Zanette D H López D 2012 Nat. Commun. 3 806
[27] Ning B Zhang S Y Hou D Wu J T Li Z B 2014 Sci. Rep. 4 5109
[28] Affolderbach C Mileti G A 2005 Rev. Sci. Inst. 76 073108
[29] Ali M H Murata T Tamura J A 2005 International Conference on Power Electronics and Drives Systems November 28–December 1, 2005 Kuala Lumpur, Malaysia 1566 10.1109/PEDS.2005.1619938
[30] Lee H Suh M G Chen T Li J Diddams S A 2013 Nat. Commun. 4 2468
[31] Le N P T Low K T Yao L 2009 IEEE 8th International Conference on ASIC October 20–23, 2009 IChangsha, Hunan, China 363 10.1109/ASICON.2009.5351417
[32] Michaelsen J Wisland D A 2010 17th IEEE International Conference on Electronics, Circuits and Systems December 12–15, 2010 Athens, Greece 1132 10.1109/ICECS.2010.5724716
[33] Shuai D X Zhang X P 2010 International Conference on Electrical Machines and Systems October 10–13, 2010 Incheon, South Korea 329
[34] Frank S Dominik J 2005 Phys. Rev. 72 042324
[35] Chumak A V Tiberkevich V S Karenowska A D Serga A A Gregg J F 2010 Nat. Commun. 1 749
[36] Okuni H Ito R Yoshida H Itakura T A 2007 IEEE 18th International Symposium on Personal, Indoor and Mobile Radio Communications September 3–7, 2007 Athens, Greece 1 10.1109/PIMRC.2007.4394571
[37] Kenji N Amy K Jordan C 2004 Phys. Rev. Lett. 93 250602
[38] Traverso P A Florian C Borgarino M Filicori F 2006 IEEE Trans. Microw. Theory Tech. 54 4341
[39] Dai C X Yin Z D Hong Q Kong S H 2010 5th IEEE Conference on Industrial Electronics and Applications June 15–17, 2010 Taichung, Taiwan 989 10.1109/ICIEA.2010.5515746
[40] Ye Y X Xuan Z Q Gu J S Xuan Y 2014 Chin. Phys. 23 120601
[41] Neumann A Anders W Kugeler O Knobloch J 2010 Mod. Phys. 13 3280
[42] Lei S H Han Y H Li X W 2007 16th Asian Test Symposium (ATS) October 8-11 2007 Beijing, China 323 10.1109/ATS.2007.35
[43] Lanin A A Fedotov I V Fedotov A B Sidorov-Biryukov D A Zheltikov A M 2013 Sci. Rep. 3 1842
[44] Liang S Li D H Gao X Y 2007 8th International Conference on Electronic Measurement and Instruments August 16–18, 2007 Xi’an, China 1563 10.1109/ICEMI.2007.4350512
[45] Williams S R Wozny C 2011 Nat. Commun. 2 242
[46] Li J Y Luo L F Xu J Z Zeng J H 2010 International Conference on Intelligent System Design and Engineering Application October 13–14, 2010 Changsha, China 174 10.1109/ISDEA.2010.170
[47] Acharya B A John V 2010 Joint International Conference on Power Electronics, Drives and Energy Systems December 20-23, 2010 New Delhi, India 1 10.1109/PEDES.2010.5712470
[48] Li S H Liaw C M 2003 IEE Proceedings — Electric Power Applications April 08, 2003 IET 21 10.1049/ip-epa:20020582
[49] Huang Y Y Hamhee J Yoon Y Woo W Lee C Kenney J S Chang-Ho L Kenney J S 2012 IEEE Trans. Microw. Theory Tech. 60 301
[50] Seung-Hoon L Bang-Sup S 1992 IEEE J. Solid-State Circuits 27 1679
[51] Ruocco G Fratalocchi A 2014 Sci. Rep. 4 7088