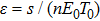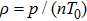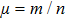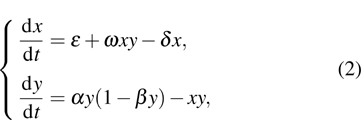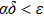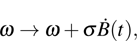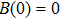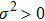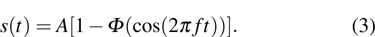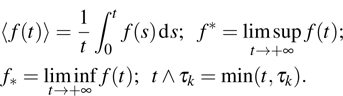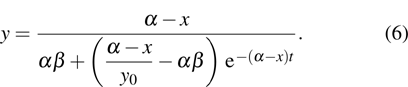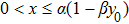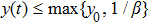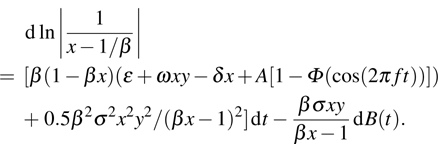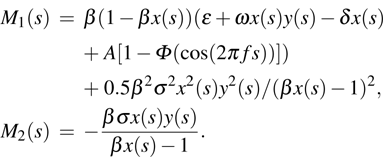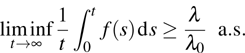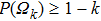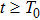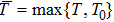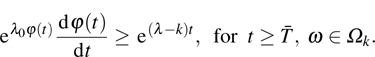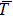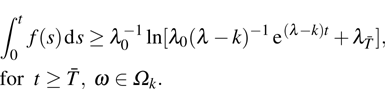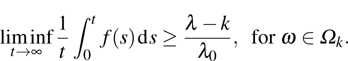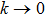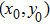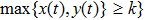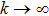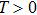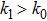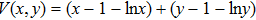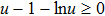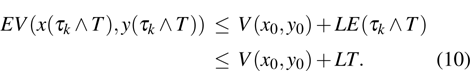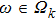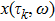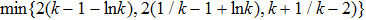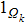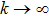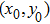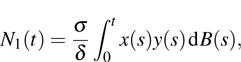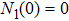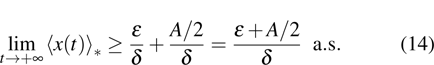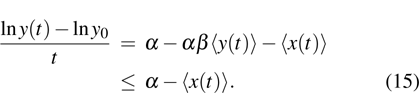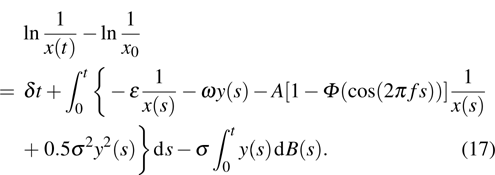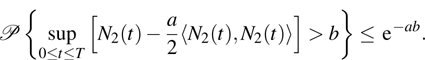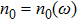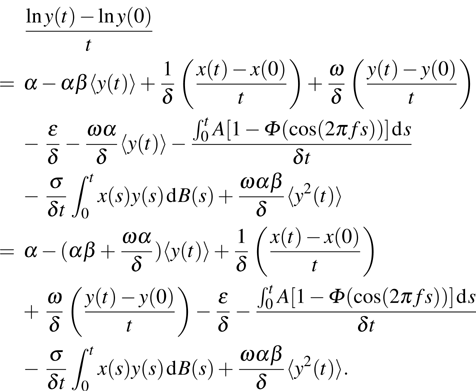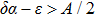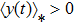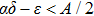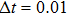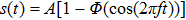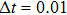1. IntroductionCancer is becoming the leading cause of death around the world. Traditional cancer treatments include surgery, radiation therapy, and chemotherapy. Cancer immunotherapy has recently gained exciting progress. Studies of tumor and immune system have largely been inspired by the works in Refs. [1] and [2], the authors showed that the immune system can recognize and eliminate malignant tumors. So immunotherapy, such as the cellular immunotherapy,[3] has been studied by researchers. And a number of tumor–immune system competition models have been proposed, such as Kuznetsov–Taylor model[4] and Kirschner–Panetta model.[5] In fact, tumor microenvironment is inevitably affected by environmental noise in realism. Nowadays, noise dynamics have been widely studied in different fields such as metapopulation system[6] and Van der Pol oscillator.[7] In the last years, researchers have studied stochastic growth models of cancer cells,[8–11] using the Lyapunov exponent method and the Fokker–Planck equation method to investigate the stability of the stochastic model. Moreover, from a biological or a clinical point of view, investigations including treatments such as periodic ones are important for a successful treatment, e.g., Thibodeaux and Schlittenhard[12] investigated the effect of a periodic treatment in the within-host dynamics of malaria infection and suggested that synchronization with the intrinsic oscillation of infected erythrocytes takes place, leading to an optimal treatment. Sotolongo et al.[13] investigated the effect of immunotherapy under periodic treatment on a deterministic model of tumor–immune system and considered the possibility of suppression of tumor growth. Ideta et al.[14] considered the intermittent hormonal therapy in a model of prostate cancer and they suggested the existence of an optimal protocol to the intermittent therapy. Up to now, the effect of noise and cyclic treatment in the tumor dynamics has been widely studied. And fluctuations induced extinction and stochastic resonance in a model of tumor growth with periodic treatment have been studied.[15] Aisu and Horita[16] numerically investigated the stochastic extinction of tumor cells due to the synchronization effect through a time periodic treatment in a tumor–immune interaction model.
The aim of this paper is to explore the dynamics of a simplified Kuznetsov–Taylor model[17] with both environmental noise and periodic treatment, especially the extinction and persistence. One of the advantages of our study is that we make use of the methods of Itô’s stochastic integral and Lyapunov function to derive and analyze the properties of the stochastic tumor–immune system competition model, which is different from the approaches of Fokker–Planck equation and effective potential function used in the existing literature. The other advantage is that the conditions for extinction and strong persistence in the mean of tumor cells are obtained by the strict mathematical proofs. The sufficient conditions for extinction and persistence could provide us a more effective and precise therapeutic schedule to eliminate tumor cells and improve the treatment of cancer.
This paper is organized as follows. In Section 2, the stochastic tumor–immune model with periodic treatment is derived. In Section 3, we establish the sufficient conditions for extinction and strong persistence in the mean of tumor cells. Numerical simulations are presented in Section 4, which are used to verify and illustrate the theorems of Section 3. In Section 5, we present the conclusion and discuss future directions of this research.
2. Stochastic tumor–immune system with periodic treatmentIn this section, the Kuznetsov–Taylor model[4] and its modified version by Galach[17] are introduced. The Kuznetsov–Taylor model describes the response of effector cells to the growth of tumor cells and takes into account the penetration of tumor cells by effector cells, which simultaneously causes the inactivation of effector cells. The Kuznetsov–Taylor model reads
where
s is the normal (i.e., not increased by the presence of the tumor) rate of the flow of adult effector cells into the tumor site in units of cells per day,
p and
g are positive constants in the function

that describes the accumulation of effector cells in the tumor site,
p is in units of day
−1 and
g is in units of cells.
m denotes the coefficient of inactivation of effector cells during the formation and decomposition of EC-TC compounds and is in units of

.
d is the coefficient of the destruction and migration of effector cells and is in units of day
−1.
a is the coefficient of the maximal growth of tumor and is in units of day
−1.
b−1 is the environment capacity, and
b is in units of cells
−1.
n represents the inactivation rate of tumor cells due to the immune system response and is in units of day
−1 
cells
−1. The dimensionless form of the model is
where

,

,
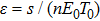
,
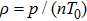
,

,
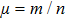
,

,

,

, and

cells.
In 2003, Galach proposed the modified version of model (1), which reads
where
x denotes the dimensionless density of effector cells;
y stands for the dimensionless density of the population of tumor cells;
ε,
δ,
α,

have the same meanings as those in Eq. (
1), and
ω represents the immune response to the appearance of the tumor cells (i.e.,immune coefficient). In this paper, we consider the case of

, which means that the immune response is positive.
System (2) always has the equilibrium
If

and
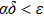
, then
P0 is the unique equilibrium of model (
2) and it is globally stable. If

and

, then
P0 is unstable and there is an equilibrium
which is globally stable. Here

.
In fact, the growth of tumor cells is influenced by many environmental factors,[18] e.g., the supply of oxygen and nutrients, the degree of vascularization of tissues, the immunological state of the host, chemical agents, temperature, etc. So, it is inevitable to consider the tumor–immune system competition model with environmental noises. In this paper, taking into account the effect of randomly fluctuating environment, we assume that the fluctuations in the environment mainly affect the immune coefficient ω,
where

is the standard Brownian motion with
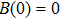
, and the intensity of white noise
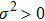
. We are interested in the stochastic responses of the tumor immune system driven by a controllable therapy. Here, the influence of the therapeutic factors is studied by considering a periodic treatment (chemo- or radiation-therapy). The treatment scheme
[19] can be expressed as
Here

stands for the Heaviside function reflecting the on-off switch of the cyclic treatment performed with the intensity
A and frequency
f. Now the tumor–immune system competition model with environmental noise and periodic treatment can be rewritten as
where all the parameters are positive and bounded. For convenience, we define the following notions:
3. Theoretical analysis of extinction and persistence under periodic treatmentOur primary interests in tumor dynamics are the extinction and survival of tumors. In order to study the extinction and survival, we need some appropriate definitions about extinction and persistence. Here we adopt the concepts of extinction and strong persistence in the mean.[20] In addition, some of our proofs are motivated by the works of Liu,[20] Mao,[21] and Jiang.[22] Some useful definitions are as follows:
1) The tumor cells  will go to extinction a.s. if
will go to extinction a.s. if  .
.
2) The tumor cells 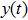 will be strongly persistent in the mean a.s. if
will be strongly persistent in the mean a.s. if 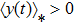 .
.
Next we establish the sufficient conditions of extinction and persistence for our model.
Lemma 1 For any positive initial value  , if
, if  , the solution of Eq. (4) obeys
, the solution of Eq. (4) obeys
Proof According to the second equation of model (4), we have
Firstly, we discuss
y for
x in different value ranges.
(i) When  (i.e.,
(i.e., 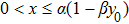 ),
),
(ii) When

(i.e.,

),
(iii) When

(i.e.,

),
Consequently, we have proved
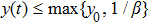
. Then we will show that

is bounded. Applying the Ito’s formula
[23] to the first equation of model (
4),
Integrating both sides from 0 to
t, we obtain
where
Therefore,
That is to say if

, then

for all

.
Lemma 2 Let  and
and 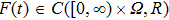 . If there exist positive constants
. If there exist positive constants  , and T such that
, and T such that
for all

, and

a.s., then
Proof The proof is similar to that of lemma in Ref. [22]. Note that  ; then for arbitrary
; then for arbitrary  , there exists a
, there exists a 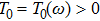 and a set
and a set  such that
such that 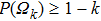 and
and  for all
for all 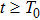 ,
,  . Let
. Let 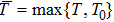 and
and
Since

, then

is differentiable on

a.s., and
Substituting

and

into Eq. (
7), we obtain
Thus
Integrating this inequality from
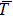
to
t results in
This inequality can be rewritten as
Taking the logarithm of both sides yields
where
or
Dividing both sides by
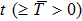
gives
Taking the limit inferior of both sides and applying L’Hospital’s rule on the right-hand side of this inequality, we obtain
Letting
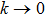
yields
Theorem 1 For any positive initial value 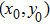 , particularly, when
, particularly, when  , equation (4) has a positive unique global solution
, equation (4) has a positive unique global solution  on
on  a.s.
a.s.
Proof To obtain a unique global solution for any given initial value, the coefficients of the equation are generally required to satisfy the linear growth condition and local Lipschitz condition.[24] However, the coefficients of model (4) do not satisfy the linear growth condition, so the solution may explode in a finite time. Since the coefficients of Eq. (4) are locally Lipschitz continuous for any given initial value  , there is a unique maximal local solution
, there is a unique maximal local solution  on
on  , where
, where  is the explosion time.[24] To show that this solution is global, we only need to show
is the explosion time.[24] To show that this solution is global, we only need to show  . To this end, let
. To this end, let  be sufficiently large so that x0,y0 all lie within the interval
be sufficiently large so that x0,y0 all lie within the interval  . For each integer
. For each integer  , we define the stopping time
, we define the stopping time  :
:  or
or 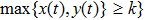 . Clearly, τk is increasing as
. Clearly, τk is increasing as 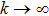 . Set
. Set  , thus
, thus  a.s. In other words, we only need to prove
a.s. In other words, we only need to prove  . If this statement is false, there exists constants
. If this statement is false, there exists constants 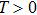 and
and  such that
such that  . Thus there is an integer
. Thus there is an integer 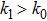 such that
such that
Define a
C2-function

by
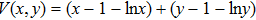
. The nonnegativity of this function can be seen from
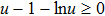
,

. Let

and

be arbitrary. Applying the Itô’s formula, we have
Here,
L is a positive constant and in the proof of the last inequality, we have used Lemma 3 (i.e., for

,

and

are bounded). The inequality (
9) implies
Taking expectation on both sides of the above inequality, we can obtain
Let

, then by inequality (
8), we have

. Note that for any
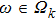
,
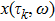
,

equals either
k or

, hence

is no less than
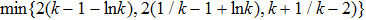
. By formula (
10) we have
where
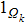
is the indicator function of

. Let
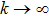
, there exists the contradiction

, which completes the proof.
Remark 1 In order to guarantee the existence and uniqueness of the solution of model (4), we discuss the extinction and persistence of  under the condition
under the condition  below.
below.
Theorem 2 Let  be the solution of system (4) with positive initial value
be the solution of system (4) with positive initial value 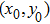 , if
, if  , then
, then
Proof An integration of the first equation of model (4) yields
We compute
where
which is a local continuous martingale and
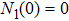
. Moreover
By strong law of large numbers for local martingales,
[24] we obtain
Taking the limit inferior of both sides of inequality (
12), we have
Applying the Itô’s formula to the second equation of model (
4) yields
Integrating this from 0 to
t and dividing by
t on both sides, we have
Taking the limit superior of both sides of inequality (
15) and substituting inequality (
14) into inequality (
15) yield
If the condition

is satisfied, then
which implies
Applying the Itô’s formula to the first equation of model (
4) leads to
Integrating this from 0 to
t, we have
Set

, whose quadratic variation is
By virtue of the exponential martingale inequality,
[24] for any positive constants
T,
a, and
b, we have
Choosing
T=
n,
a=1, and

we obtain
An application of Borel–Cantelli lemma
[22] yields that for almost all

, there is a random integer
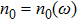
such that for

,
That is to say,
for all
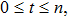

a.s. Substituting the above inequality into inequality (
17) leads to
Let
obviously,

. By use of Lemma 3, we have
namely,
With inequalities (
18) and (
14), we see
Theorem 3 If  , then the tumor cells
, then the tumor cells  will be almost surely strong persistent in the mean.
will be almost surely strong persistent in the mean.
Proof An integration of system (4) is
Then we have
We compute
Applying the Itô’s formula to system (
4) leads to

. Integrating this from 0 to
t and dividing by
t on both sides, we have
Substituting Eq. (
20) to Eq. (
21) yields
We compute
Considering that both

and

are bounded, we have
Consequently, we can derive that if
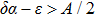
, then
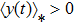
a.s.
4. Simulations and discussionIn this section, we use the Euler–Maruyama numerical algorithm mentioned by Higham[25] to support our results. The parameters in model (4) are chosen as α=1.636, β=0.002, δ=0.3743, ε=0.5181, and ω=0.0115, which are approximated to the experimental values.[4,17]
Figure 1 shows the simulation results of Theorem 2. Clearly, the parameters satisfy the condition 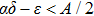 . In view of Theorem 2, the tumor cells
. In view of Theorem 2, the tumor cells  will go to extinction, and the effector cells
will go to extinction, and the effector cells  have the property
have the property  figure 1 confirms the results of Theorem 2.
figure 1 confirms the results of Theorem 2.
Figure 2 shows the simulation results of Theorem 2. In Fig. 2, it is clear that the parameters of the example meet the condition  . According to Theorem 2, the tumor cells
. According to Theorem 2, the tumor cells  will be almost surely strongly persistent in the mean. It can be seen from Fig. 2 that the tumor cells will decrease firstly and then exhibit a period-like evolution at a relative low concentration under periodic treatment, but do not tend to zero. This phenomenon implies that the tumor cells could be suppressed by the periodic treatment but not be completely eliminated when the intensity of the treatment is not enough to cure the tumor, i.e., the tumor cells could be controlled and will not deteriorate in this case. Moreover, it can be seen that as long as the conditions of persistence
will be almost surely strongly persistent in the mean. It can be seen from Fig. 2 that the tumor cells will decrease firstly and then exhibit a period-like evolution at a relative low concentration under periodic treatment, but do not tend to zero. This phenomenon implies that the tumor cells could be suppressed by the periodic treatment but not be completely eliminated when the intensity of the treatment is not enough to cure the tumor, i.e., the tumor cells could be controlled and will not deteriorate in this case. Moreover, it can be seen that as long as the conditions of persistence  are satisfied, the tumor cell will be strongly persistent in the mean almost surely when the model is with noise. And, the tumor cells will also be persistent or survival when the model is without noises. The difference is that the persistence of the former is in the sense of the mean, which is random; while the persistence of the latter is expressed as persistence or survival, which is deterministic.
are satisfied, the tumor cell will be strongly persistent in the mean almost surely when the model is with noise. And, the tumor cells will also be persistent or survival when the model is without noises. The difference is that the persistence of the former is in the sense of the mean, which is random; while the persistence of the latter is expressed as persistence or survival, which is deterministic.
Figure 3 shows the evolution of tumor cells  as a function of time t for three different values of A=0.07, 0.3, 3. Clearly, when A is 0.07, it satisfies the condition
as a function of time t for three different values of A=0.07, 0.3, 3. Clearly, when A is 0.07, it satisfies the condition  . According to Theorem 2, the tumor cells
. According to Theorem 2, the tumor cells  will be strongly persistent in the mean. With increasing strength of the treatment, A is taken as 0.3 or 3, they satisfy the condition
will be strongly persistent in the mean. With increasing strength of the treatment, A is taken as 0.3 or 3, they satisfy the condition  . According to Theorem 2, the tumor cells
. According to Theorem 2, the tumor cells  will tend to be extinction. Moreover, by comparing curves (ii) and (iii), we find that the tumor cells will be extinct faster with the increase of the treatment intensity A. This behavior indicates that increasing the intensity of the treatment is beneficial to accelerate the extinction of the tumor cells.
will tend to be extinction. Moreover, by comparing curves (ii) and (iii), we find that the tumor cells will be extinct faster with the increase of the treatment intensity A. This behavior indicates that increasing the intensity of the treatment is beneficial to accelerate the extinction of the tumor cells.
5. ConclusionWe study stochastic responses of a tumor–immune system competition model with environmental noise and periodic treatment. Firstly, the environmental noise (Gaussian white noise) is taken into account and the periodic treatment is regarded as a Heaviside function. Then, sufficient conditions for extinction and strong persistence in the mean of tumor cells are derived by constructing Lyapunov functions. The detail results and biological significance are as follows:
(A) If  , then the effector cells
, then the effector cells  have property
have property  , and the tumor cells
, and the tumor cells  will go to extinction a.s.
will go to extinction a.s.
(B) If  , then the tumor cells
, then the tumor cells  will be strongly persistent in the mean a.s.
will be strongly persistent in the mean a.s.
According to the theorems and figures, the extinction and survival of the tumor cells rely on the strength of the periodic treatment. With the increasing intensity of the periodic treatment, the tumor cells will experience the process from strongly persistence in the mean to extinction. In addition, the synchronization effect between the environmental noises and the periodic treatment on the tumor–immune system competition model is obtained by strict proof and simulation. Our theoretical results will be beneficial to design more effective and feasible treatment therapies.
Some interesting questions deserve further investigations. For example, in our model, we assume that fluctuations in the environment mainly affect the immune coefficient ω. It is interesting to study what happens if it affects other parameters of the tumor–immune system. Another question of interest is to consider the stability in distribution (e.g., Refs. [26] and [27]) and time delay (e.g. Ref. [28]) of the tumor–immune system.