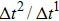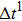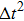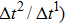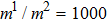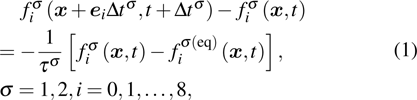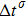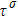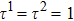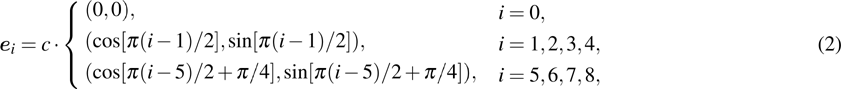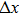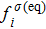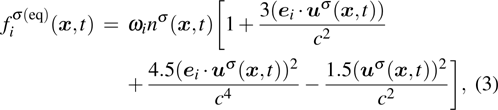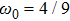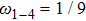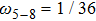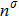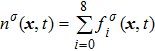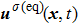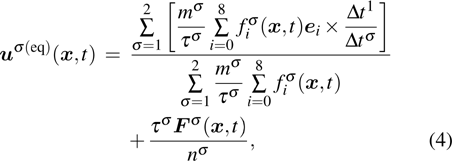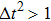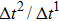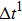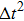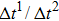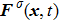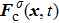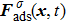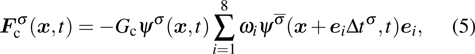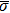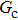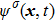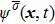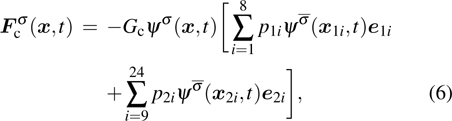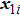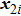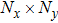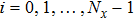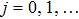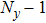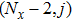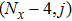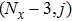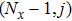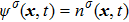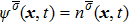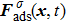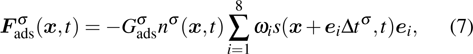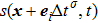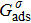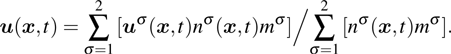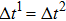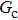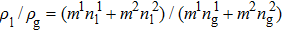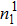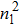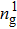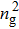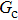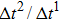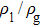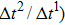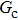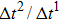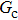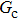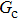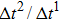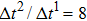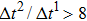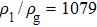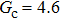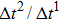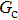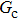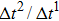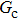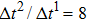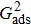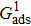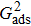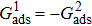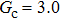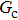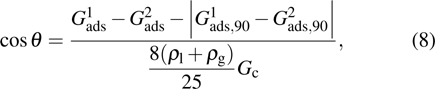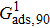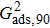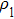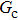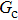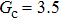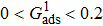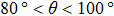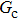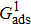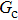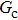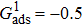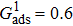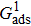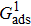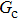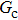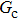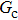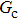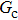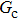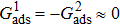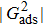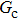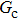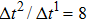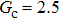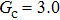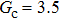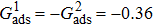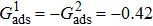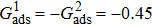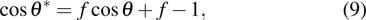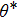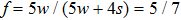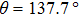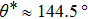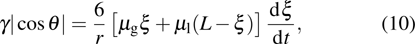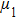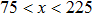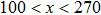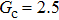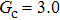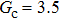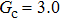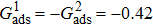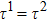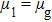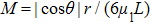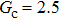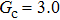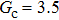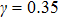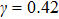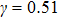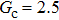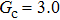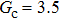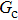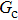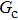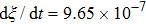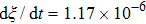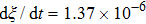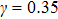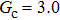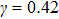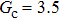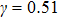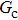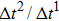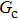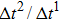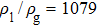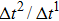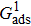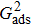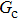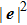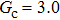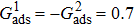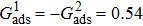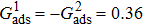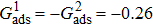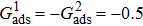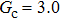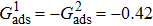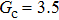1. IntroductionOver the last three decades, multiphase lattice Boltzmann (LB) models have developed rapidly and have been employed extensively in the field of computational fluid dynamics.[1–8] As a result of LB models not needing to explicitly track interfaces, these models are ideally suited to study physical phenomena in the multiphase flow systems, e.g., bubbles moving in the liquid phase,[9,10] wetting phenomena at the fluid–solid interfaces,[11–15] droplet–wall collisions,[16] and droplet splashing.[17] Among the current multiphase LB models, the pseudopotential LB scheme has attracted a lot of attention due to its computational efficiency and simplicity in coding.[1–5] The pseudopotential LB model imposes non-local interactions among fluid particles. Accordingly, when the interaction potentials are appropriately chosen, different fluid phases can be separated automatically.[8–21] The original multiphase pseudopotential LB model proposed by Shan and Chen[18] is, however, essentially limited to a small density ratio between the two fluid phases, owing to the increased spurious current at the curved interface between different phases.[1–3] As a result, the model becomes inappropriate for some real-world multiphase fluid flows with large density ratios, such as the water-vapor system.
Many efforts have been devoted to improving the performance of pseudopotential LB models, in particular to increasing the liquid–gas density ratio.[21–42] For single component multiphase (SCMP) LB models, there are two typical techniques to enlarge the density ratio of the two fluid phases: (i) introducing realistic equations of state (EOS),[21–23] and (ii) increasing the isotropy order of the interaction force.[24–28] Yuan and Schaefer[21] proposed an LB model in which the pseudopotential equations were derived from the different EOSs, rather than straightforwardly defined as a function of local density. By incorporating the appropriate EOS into the LB models, such as employing the Carnahan–Starling[22] or van der Waals[23] real gas EOS, the liquid–gas density ratio could increase to higher than 1000:1.
As mentioned above, in the original LB models, the spurious current appearing near a curved phase interface deteriorates the stability of calculations and thus restricts the density ratio of the liquid–gas phases to a small range.[24] To solve the problem, researchers have made efforts to seek the best compromise between a large liquid–gas density ratio and small spurious current.[25–28] Shan[25] considered that the spurious currents existing in the multiphase LB models are caused by insufficient isotropy of the discrete gradient operator. He calculated the interaction force with higher order symmetry, and hence the spurious current effectively decreased. Sbragaglia et al.,[26] and Falcucci et al.[27,28] introduced a mid-range potential interaction into the pseudopotential LB models using two layers of neighboring nodes to calculate the interaction force. Using this approach, the spurious currents at the phase interfaces are diminished by the higher isotropy order. Other techniques, aiming at reducing the spurious currents to increase the liquid–gas density ratios of the pseudopotential LB models, include grid refinement,[29,30] adopting proper force schemes,[31–35] and using the multi-relaxation-time scheme.[36–38]
All the above approaches concern SCMP LB models. In contrast, there are few reports on increasing the liquid–gas density ratios of multicomponent multiphase (MCMP) pseudopotential LB models, yet it is well known that many multiphase flows in nature and practice are composed of multiple chemical components, such as water–air and alloy melt–hydrogen gas flow systems. Liu et al.[39] and Chen et al.[40] elevated the liquid–gas density ratio to a value of higher than 100:1 by imposing an interaction force among the same component particles in the MCMP model. Bao and Schaefer[41] also incorporated the interaction force among the same component particles, which was set to be 103 times higher than that among the different component particles in previous MCMP models. Using such an approach, the density ratio was increased to 1000:1. This approach presents a weakness, because the imposed interaction force among the same component particles might give rise to some problems. For example, it affects the solubility of one component in the other components.[1] Moreover, it also limits the achievable contact angle ranges of droplets on solid surfaces.[40] Another important topic in the field of the MCMP pseudopotential LB model is to implement the different molecular weights (pseudo-particle mass) with respect to the different fluid components. The approaches that have been proposed include (i) applying the interpolation technique or modifying the equilibrium distribution function to derive the distribution functions for different fluid components[43,44] and (ii) adopting the finite-different-based LB model.[45] The two approaches are feasible when the time steps of the different fluid components are identical. However, the studies of adopting different time steps with respect to the different fluid components remain limited in the literature.
In the present work, based on the original MCMP pseudopotential LB model developed by Shan and Chen,[18] a modified MCMP pseudopotential LB model is proposed to simulate the liquid–gas flow with large density contrasts. In the present model, the interaction force among the same component particles is not considered. Instead, we employ a scheme that adopts higher isotropy order to calculate the interaction force, and is combined with a different time step method. Using this approach, the liquid–gas density ratio is enlarged, and the spurious current is restricted for the multicomponent multiphase system. The proposed model is used to simulate the wetting behavior of droplets on smooth/rough solid surfaces and the dynamic process of liquid movement in a capillary tube. The simulated intrinsic and apparent contact angles of the droplets on solid surfaces, as well as the simulated time evolution of the moving liquid–gas interface position in a capillary tube, are compared with theoretical predictions.
2. Model descriptionThe techniques used in the present MCMP model involve (i) using two layers of neighboring nodes to calculate the interaction forces between the two components, and (ii) adopting different time steps for the two components.
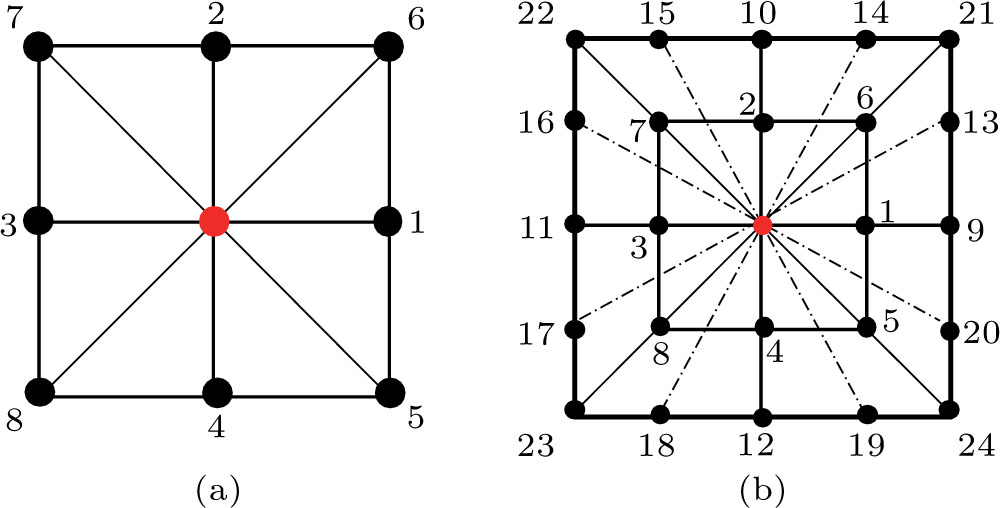
Figure 1 shows the node distributions for calculating the fluid–fluid cohesion force in the original and present pseudopotential LB models, respectively. As shown in Fig. 1(a), only the nearest nodes (nodes 1, 2, 3, 4) and the next-nearest nodes (nodes 5, 6, 7, 8) are considered in the original model to calculate the cohesion force, yielding the fourth isotropy order (E4).[25] In the present model, however, two layers of neighboring nodes (24 nodes) are used to calculate the cohesion force as shown in Fig. 1(b), obtaining the eighth isotropy order (E8) that can reduce the spurious currents at the phase interface.[25–28,42] In addition, the time step of component 2 (the essential component in the gas phase) is set to be larger than that of component 1 (the essential component in the liquid phase), so that the components with a large pseudo-particle mass contrast can be implemented. This scheme takes into account the fact that the mean free path of gas particles is longer than that of liquid particles. This causes the period of component 2 for accomplishing the processes of propagation and collision to be 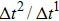 times longer than that of component 1, where
times longer than that of component 1, where 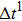 and
and 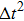 are the time steps of component 1 and component 2, respectively. Accordingly, the time step ratio (
are the time steps of component 1 and component 2, respectively. Accordingly, the time step ratio (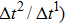 between the two components is set to be
between the two components is set to be  based on the E8 MCMP LB model. It is noted that the computation efficiency of the present MCMP model is inversely proportional to the value of the time step ratio. The pseudo-particle mass ratio between the two components is assumed to be
based on the E8 MCMP LB model. It is noted that the computation efficiency of the present MCMP model is inversely proportional to the value of the time step ratio. The pseudo-particle mass ratio between the two components is assumed to be 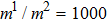 . This magnitude of
. This magnitude of  is selected according to the large weight ratios of fluid particles in real-world liquid–gas systems, such as alloy melt–hydrogen gas flows.
is selected according to the large weight ratios of fluid particles in real-world liquid–gas systems, such as alloy melt–hydrogen gas flows.
The two fluid components are represented by two sets of distribution functions. The processes of particle propagation and collision are governed by the LB equations using the two-dimension, nine-velocity (D2Q9) scheme:
where

,
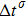
, and
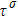
are the density distribution function, the time step, and the relaxation time of the
σ-th component, respectively. The relaxation times of the two components are adopted to be
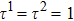
in the present study. Discrete velocities,
, in the D2Q9 scheme are given by
where

is the lattice speed, and
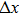
is the lattice spacing. The equilibrium distribution function,
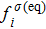
, is expressed as
where the weight coefficients
ωi are given as
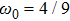
,
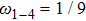
, and
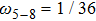
, and
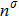
is the number density of the
σ-th component, which is obtained from
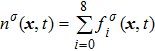
. Based on the original MCMP pseudopotential LB model, the time step-related macroscopic velocity
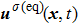
is given by
where
mσ is the pseudo-particle mass of the
σ-th component. In the present study, the time steps of components 1 and 2 are assumed to be

and
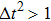
, respectively. Since component 1 accomplishes the propagation and collision processes
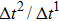
times with
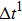
, while component 2 accomplishes it once with
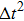
, it is considered that the microscopic velocity of component 1 should interact with that of component 2
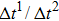
times. Therefore, in the numerator of the first term on the right-hand side of Eq. (
4), the time steps are taken into consideration when calculating the microscopic momentum.
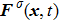
in Eq. (
4) is the interaction force acting on the
σ-th component, which includes the fluid–fluid cohesion force
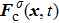
and the fluid–solid adhesion force
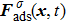
.
In the original MCMP pseudopotential LB model with E4 isotropy order, the fluid–fluid cohesion force acting on the σ-th component, which generates different fluid phases, is calculated from
where
σ and
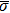
denote the two different fluid components,
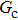
is the fluid–fluid interaction strength that controls the cohesion force and surface tension between two fluid phases, and
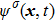
and
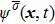
are the pseudopotential functions.
As described above, for reducing the spurious current at the phase interface, the present model adopts the E8 isotropy order to calculate the cohesion force. Accordingly, equation (5) is rewritten as
where
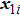
and
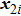
denote the first layer (nodes 1–8 in Fig.
1(b)) and the second layer (nodes 9–24 in Fig.
1(b)) of the neighboring nodes, respectively. The numerical values of the weight coefficients, namely,
p1i and
p2i, are listed in Table
1.
[25–28,42] In the present study, the periodic boundary condition is imposed on the walls of the computational domain. For the domain consisting of
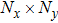
computational nodes, the node index is assumed to be
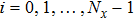
in the
x-axis direction and
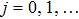
,
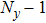
in the
y-axis direction, respectively. When the cohesive forces are calculated by using Eq. (
6), the neighboring nodes of the fluid particles at nodes
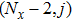
(close to the right boundary) involve those located at the positions of
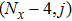
,
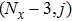
,
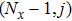
(the right boundary), and (0,
j) (the left boundary), respectively. The same approach is used for the neighboring nodes of the fluid particles located at the layers close to the other boundaries. The pseudopotential functions of the two fluid components are taken as fluid number densities, which are
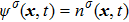
and
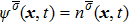
, respectively.
Table 1.
Table 1.
 Table 1.
Weight coefficients of the E8 model.[25–28,42]
.
| Nodes |
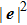 |
p1i |
p2i |
| 1–4 |
1 |
4/21 |
|
| 5–8 |
2 |
4/45 |
|
| 9–12 |
4 |
|
1/60 |
| 13–20 |
5 |
|
2/315 |
| 21–24 |
8 |
|
1/5040 |
| Table 1.
Weight coefficients of the E8 model.[25–28,42]
. |
When the system includes a solid phase, the fluid–solid adhesion force, 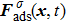 , acting on the σ-th component is computed from
, acting on the σ-th component is computed from
where
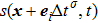
is an indicator function that is equal to 1 or 0 for a solid or a fluid neighboring node, respectively. The interaction strength between the fluid and solid phases can be adjusted by the fluid–solid interaction parameter,
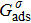
. In the present work, a bounce-back rule is adopted on the fluid–solid boundaries.
3. Results and discussion3.1. Spurious currentIn the present study, the spurious current is calculated from
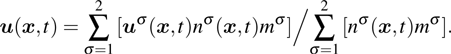 | |
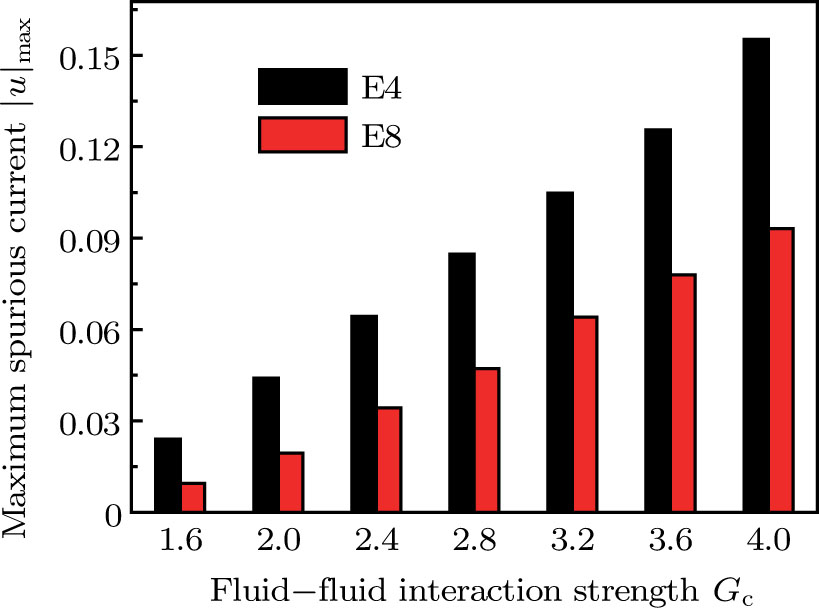
The E8 model, having a higher isotropy order than the original E4 model, is adopted to reduce the spurious current that may deteriorate the stability of the LB model. In order to examine the effect of spurious current reduction, the calculations of a stationary droplet equilibrated with gas phase are conducted by using the E4 and E8 MCMP LB models, respectively. For simplicity, the time steps and the pseudo-particle mass values of the two components are set to be 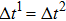 = 1 and
= 1 and 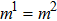 = 1 in Subsecttion 3.1, respectively. At the start of the simulation, a droplet with an initial radius of 10 lattice units is placed in the center of the computation domain that is composed of 60 × 60 lattice units. After the equilibrium states are achieved, the maximum spurious currents appearing at the liquid–gas interfaces are measured. Figure 2 shows the comparison between the maximum spurious currents obtained from the E4 LB model and those from E8 LB models. It is shown that the maximum spurious currents for both E4 and E8 models increase with the fluid–fluid interaction strength,
= 1 in Subsecttion 3.1, respectively. At the start of the simulation, a droplet with an initial radius of 10 lattice units is placed in the center of the computation domain that is composed of 60 × 60 lattice units. After the equilibrium states are achieved, the maximum spurious currents appearing at the liquid–gas interfaces are measured. Figure 2 shows the comparison between the maximum spurious currents obtained from the E4 LB model and those from E8 LB models. It is shown that the maximum spurious currents for both E4 and E8 models increase with the fluid–fluid interaction strength, 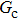 , increasing. For a given
, increasing. For a given 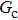 , however, the maximum spurious current in the E8 model is remarkably lower than that in the E4 model. This result accords well with the result given by Shan[25] regarding the SCMP LB model. It is shown that the implementation of the E8 model with higher isotropy order is capable of reducing the spurious current, thus effectively increasing the computation stability of the MCMP LB model.
, however, the maximum spurious current in the E8 model is remarkably lower than that in the E4 model. This result accords well with the result given by Shan[25] regarding the SCMP LB model. It is shown that the implementation of the E8 model with higher isotropy order is capable of reducing the spurious current, thus effectively increasing the computation stability of the MCMP LB model.
3.2. Liquid–gas density ratioIn this study, the liquid–gas density ratio is obtained from the calculations of a static droplet surrounded by the gas phase. The computation domain size and the initial droplet radius are identical to those in Fig. 2. After the droplet equilibrates with the surrounding gas phase, the droplet is mainly composed of component 1 with slightly dissolved component 2. In contrast, component 2 is the essential composition of the gas phase with a slight amount of component 1. Therefore, the liquid–gas density ratio is calculated from 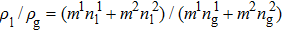 , where
, where 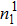 ,
, 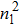 ,
, 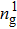 , and
, and 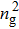 are the number densities of component 1 and component 2 in the liquid and gas phases, respectively. The liquid–gas density ratio can be affected by several factors, such as the values of the fluid–fluid interaction strength (
are the number densities of component 1 and component 2 in the liquid and gas phases, respectively. The liquid–gas density ratio can be affected by several factors, such as the values of the fluid–fluid interaction strength (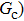 , the time step ratio (
, the time step ratio ( , the relaxation times (τ1 and τ
, the relaxation times (τ1 and τ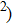 , and the pseudo-particle mass ratio (
, and the pseudo-particle mass ratio ( of the two components. In the present study, the values of τ1, τ2, m1, and m2 are assumed to be unchanged, while the effects of
of the two components. In the present study, the values of τ1, τ2, m1, and m2 are assumed to be unchanged, while the effects of 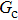 and
and 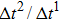 are systematically studied.
are systematically studied.
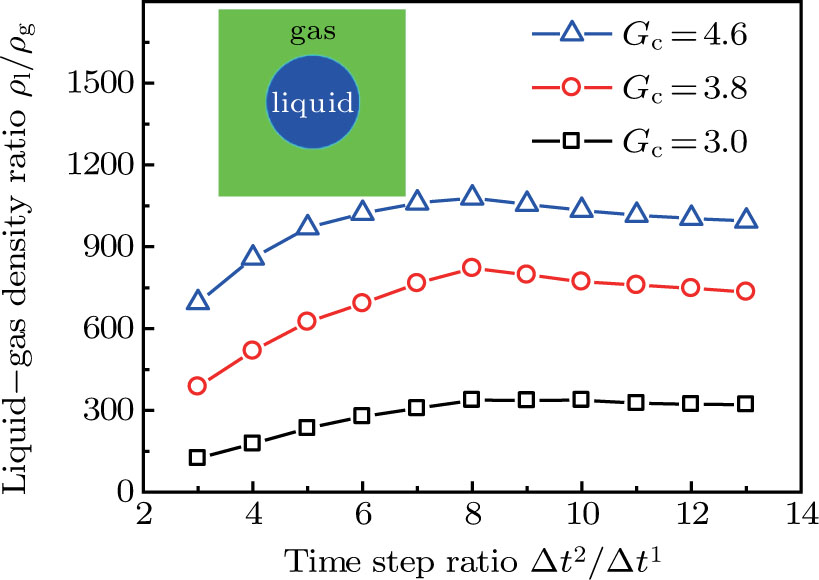
Figure 3 presents the obtained liquid–gas density ratio (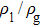 ) as a function of time step ratio (
) as a function of time step ratio (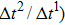 with various values of fluid–fluid interaction strength (
with various values of fluid–fluid interaction strength ( by using the proposed model. It is shown that the liquid–gas density ratio increases with
by using the proposed model. It is shown that the liquid–gas density ratio increases with 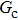 increasing when
increasing when 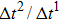 is fixed. Note that the value of
is fixed. Note that the value of 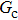 controls the separation degree of the two components. As a result, a larger
controls the separation degree of the two components. As a result, a larger 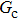 tends to reduce the solubility of component 1 in the gas phase, which accordingly reduces the gas density and elevates the liquid–gas density ratio. On the other hand, for a given
tends to reduce the solubility of component 1 in the gas phase, which accordingly reduces the gas density and elevates the liquid–gas density ratio. On the other hand, for a given 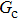 , the liquid–gas density ratio increases as
, the liquid–gas density ratio increases as 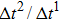 becomes larger before it approaches to a relatively stable value. It is found that as the time step ratio increases, the quantity of the fluid particles of component 1 in the gas phase gradually becomes lower, which facilitates the higher liquid–gas density ratio. Under the condition of
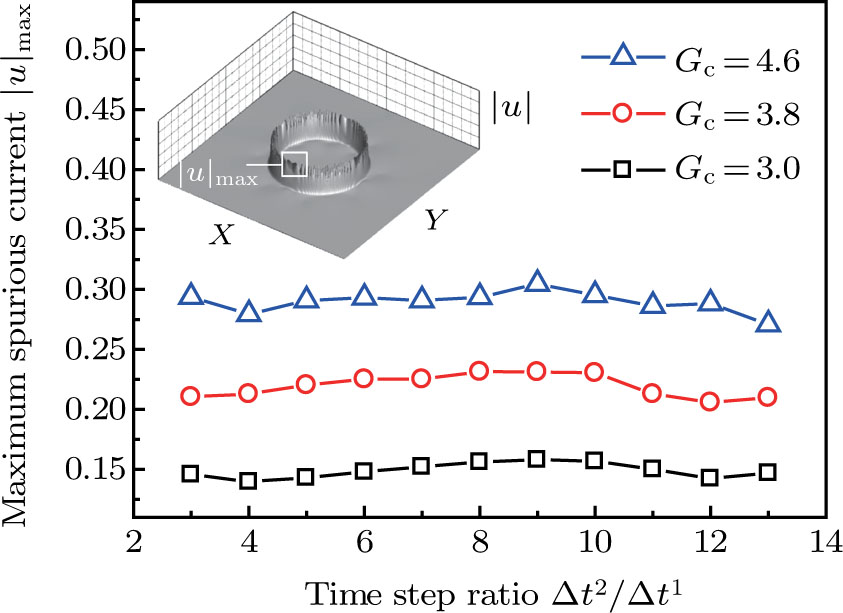
becomes larger before it approaches to a relatively stable value. It is found that as the time step ratio increases, the quantity of the fluid particles of component 1 in the gas phase gradually becomes lower, which facilitates the higher liquid–gas density ratio. Under the condition of 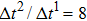 , the maximum liquid–gas density ratio is achieved. When the time step ratio is assigned as
, the maximum liquid–gas density ratio is achieved. When the time step ratio is assigned as 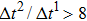 , the quantities of the fluid particles of component 1 in the liquid and gas phases almost remain stable, leading to a nearly unchanged liquid–gas density ratio. In Fig. 3, it is found that the maximum liquid–gas density ratio achieved by the present model is
, the quantities of the fluid particles of component 1 in the liquid and gas phases almost remain stable, leading to a nearly unchanged liquid–gas density ratio. In Fig. 3, it is found that the maximum liquid–gas density ratio achieved by the present model is 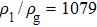 under the conditions of
under the conditions of 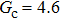 and
and  .
.
As discussed above, the spurious current appearing at the interface is one of the key factors that hinder the liquid–gas density ratio from being elevated. The influences of the fluid–fluid interaction strength 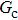 and time step ratio
and time step ratio 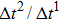 on the maximum spurious current are tested, and the results are presented in Fig. 4. The upper-left inset in Fig. 4 illustrates the map of the velocity distribution, indicating that the maximum spurious current appears at the liquid–gas interface. It can be seen from Fig. 4 that the magnitude of the maximum spurious current is strongly dependent on the fluid–fluid interaction strength
on the maximum spurious current are tested, and the results are presented in Fig. 4. The upper-left inset in Fig. 4 illustrates the map of the velocity distribution, indicating that the maximum spurious current appears at the liquid–gas interface. It can be seen from Fig. 4 that the magnitude of the maximum spurious current is strongly dependent on the fluid–fluid interaction strength 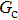 , but weakly influenced by the time step ratio
, but weakly influenced by the time step ratio  . Apparently, the maximum spurious current increases with
. Apparently, the maximum spurious current increases with 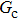 for each
for each 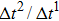 . It is found that to obtain stable calculations of a static droplet surrounded by gas phase, the maximum applicable fluid–fluid interaction strength
. It is found that to obtain stable calculations of a static droplet surrounded by gas phase, the maximum applicable fluid–fluid interaction strength 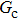 is around 4.6.
is around 4.6.
It should be noted that the maximum liquid–gas density ratios discussed above are for the case of the static multiphase flow. When the external fluid flow is introduced in the computation domain, e.g., the shear flow,[46] the achievable maximum liquid–gas density ratio is found to become lower than that obtained from the static liquid–gas flow.
3.3. Intrinsic contact angles of droplets on a smooth solid surfaceThe proposed model is used to simulate droplets on a smooth solid surface with various intrinsic contact angles. The simulation domain is composed of 100 × 100 lattice units and the droplet radius is initially taken as 15 lattice units. The time step ratio is fixed as 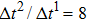 . For a given fluid–fluid interaction strength
. For a given fluid–fluid interaction strength  , the intrinsic contact angle of a droplet on a solid surface is determined by the fluid–solid interaction parameters, namely
, the intrinsic contact angle of a droplet on a solid surface is determined by the fluid–solid interaction parameters, namely 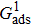 and
and 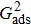 . Regarding the contact angle simulations by using the original MCMP LB model reported in the literature, the relationship between
. Regarding the contact angle simulations by using the original MCMP LB model reported in the literature, the relationship between 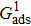 and
and 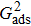 is not unique.[19,44] In the present study,
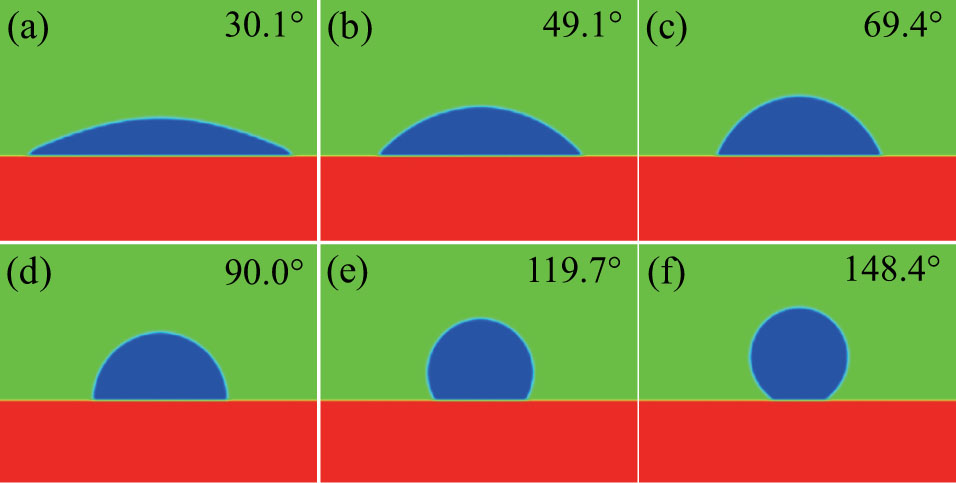
is not unique.[19,44] In the present study, 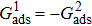 is adopted in the simulations of contact angles, which is identical with the configuration in the work of Huang et al.[47] Figure 5 illustrates droplets on a smooth solid surface with different contact angles simulated by using the corresponding values with a fixed fluid–fluid interaction strength of
is adopted in the simulations of contact angles, which is identical with the configuration in the work of Huang et al.[47] Figure 5 illustrates droplets on a smooth solid surface with different contact angles simulated by using the corresponding values with a fixed fluid–fluid interaction strength of 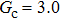 . The contact angles in Fig. 5 are measured by using the approach proposed by Huang et al.[47]
. The contact angles in Fig. 5 are measured by using the approach proposed by Huang et al.[47]
Sukop and Thorne[19] and Huang et al.[47] introduced two forms of empirical formulas that are composed of the LB interaction strengths and related to Young’s equation. The empirical formulas can be used to predict the intrinsic contact angles simulated using the original MCMP pseudopotential LB models. Since the present model implements the higher isotropy order and the different-time-step method, the previous empirical LB Young equations in the literature[19,47] are not appropriate for this work. Thus, a new empirical formula of Young’s equation is established based on the simulations of Fig. 5. The interaction strengths, 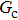 ,
,  , and
, and  which are related to the interfacial tensions between the fluid–fluid and fluid–solid phases, are rearranged to construct an empirical formula of Young’s equation as follows:
which are related to the interfacial tensions between the fluid–fluid and fluid–solid phases, are rearranged to construct an empirical formula of Young’s equation as follows:
where
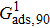
and
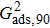
are the fluid–solid interaction strengths when the contact angle is 90°.
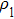
and

are the liquid and gas densities, respectively. It is noted that equation (
8) has a form similar to the empirical formula suggested by Sukop and Thorne
[19] and Huang
et al.
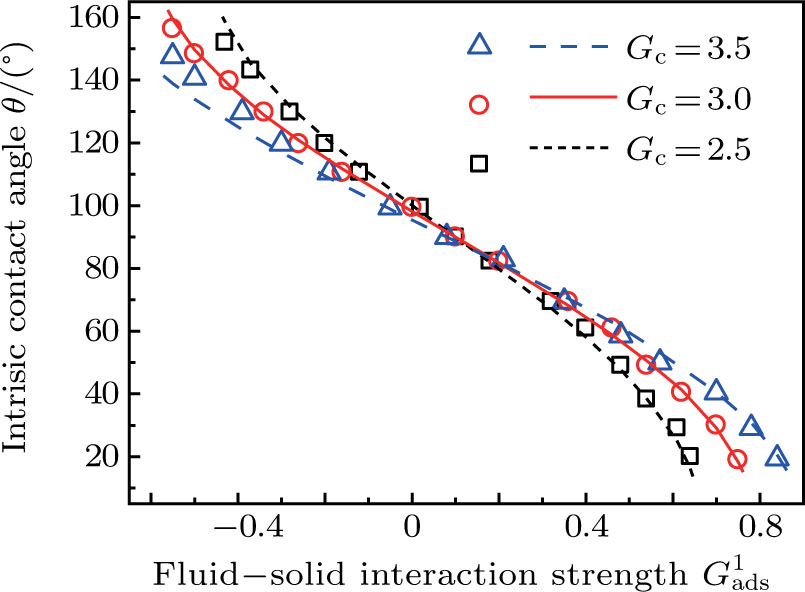
[47]Figure 6 shows the comparison between the LB simulations and calculations by Eq. (8) for the contact angles as a function of fluid–solid interaction strength with various values of fluid–fluid interaction strengths 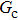 . As mentioned above, the magnitude of
. As mentioned above, the magnitude of 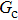 determines the surface tension and density ratio of liquid–gas phases. It can be seen that the simulated contact angles are in good agreement with those calculated by Eq. (8) for a wide range of contact angles, even though the simulations deviate slightly from the predictions of Eq. (8) in the high contact angle region for the case of
determines the surface tension and density ratio of liquid–gas phases. It can be seen that the simulated contact angles are in good agreement with those calculated by Eq. (8) for a wide range of contact angles, even though the simulations deviate slightly from the predictions of Eq. (8) in the high contact angle region for the case of 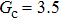 , and the maximum difference is around 8.6°. Moreover, as shown in Fig. 6, in the range of
, and the maximum difference is around 8.6°. Moreover, as shown in Fig. 6, in the range of 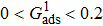 , corresponding to the contact angle region of
, corresponding to the contact angle region of 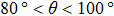 , the influence of
, the influence of 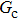 on the contact angles is relatively limited. However, as the contact angles increase or decrease, departing from 90° by regulating
on the contact angles is relatively limited. However, as the contact angles increase or decrease, departing from 90° by regulating 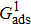 , the effect of
, the effect of 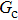 becomes increasingly evident. For example, with fixing
becomes increasingly evident. For example, with fixing  , the contact angles remain close to 90°, regardless of the variation of
, the contact angles remain close to 90°, regardless of the variation of 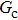 . In contrast, the contact angles can be obviously influenced by
. In contrast, the contact angles can be obviously influenced by  with selecting
with selecting 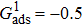 or
or 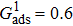 which produces high or low values of contact angles, respectively. Figure 6 also reveals that the wettability of the smooth surface increases when adopting a larger
which produces high or low values of contact angles, respectively. Figure 6 also reveals that the wettability of the smooth surface increases when adopting a larger 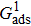 . This is because a higher magnitude of
. This is because a higher magnitude of 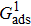 leads to a stronger adhesion force between the solid surface and component 1 that is the essential composition of the liquid droplet. The stronger adhesion force drives the droplet to spread on the surface and hence a relatively low intrinsic contact angle is obtained.
leads to a stronger adhesion force between the solid surface and component 1 that is the essential composition of the liquid droplet. The stronger adhesion force drives the droplet to spread on the surface and hence a relatively low intrinsic contact angle is obtained.
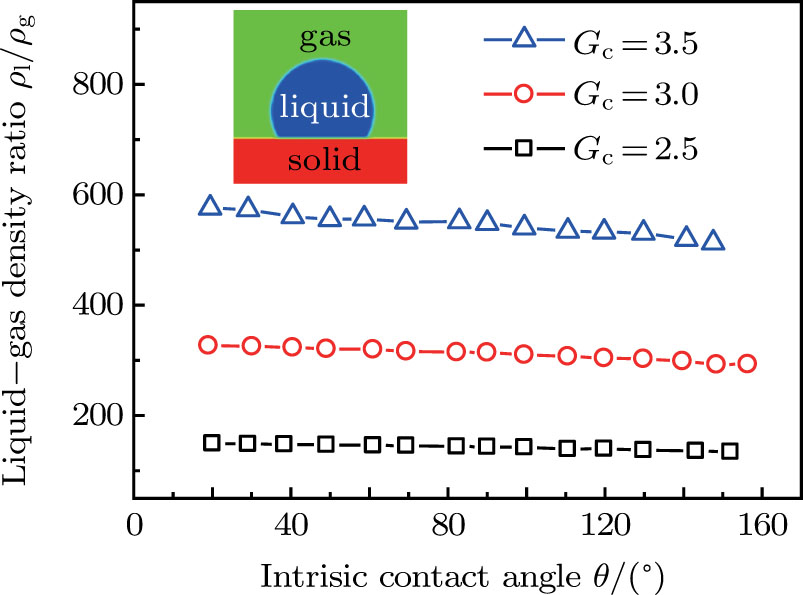
Figure 7 shows the liquid–gas density ratio in the presence of solid phase as a function of the droplet intrinsic contact angle with various values of fluid–fluid interaction strengths  . It is seen that for a fixed value of
. It is seen that for a fixed value of 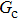 , the liquid–gas density ratio almost remains stable with a slight decreasing trend as the intrinsic contact angle becomes larger. For a fixed intrinsic contact angle, the increase of
, the liquid–gas density ratio almost remains stable with a slight decreasing trend as the intrinsic contact angle becomes larger. For a fixed intrinsic contact angle, the increase of 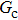 elevates the liquid–gas density ratio drastically.
elevates the liquid–gas density ratio drastically.
Comparing Fig. 7 with Fig. 3, it is found that the liquid–gas density ratio in the presence of the solid phase is nearly identical to that of the liquid–gas system without the solid phase when the same level of 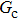 is adopted. For example, when
is adopted. For example, when  is taken to be 3.0, the liquid–gas density ratios are both around 300:1 for the two systems with and without the presence of a solid phase. However, the applicable
is taken to be 3.0, the liquid–gas density ratios are both around 300:1 for the two systems with and without the presence of a solid phase. However, the applicable 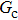 value for the solid–liquid–gas system is smaller than that for the liquid–gas system, which hinders the liquid–gas density ratios from being enlarged to a high level in the presence of a solid phase. To explain this phenomenon, the maximum spurious current is analyzed for the solid–liquid–gas system.
value for the solid–liquid–gas system is smaller than that for the liquid–gas system, which hinders the liquid–gas density ratios from being enlarged to a high level in the presence of a solid phase. To explain this phenomenon, the maximum spurious current is analyzed for the solid–liquid–gas system.
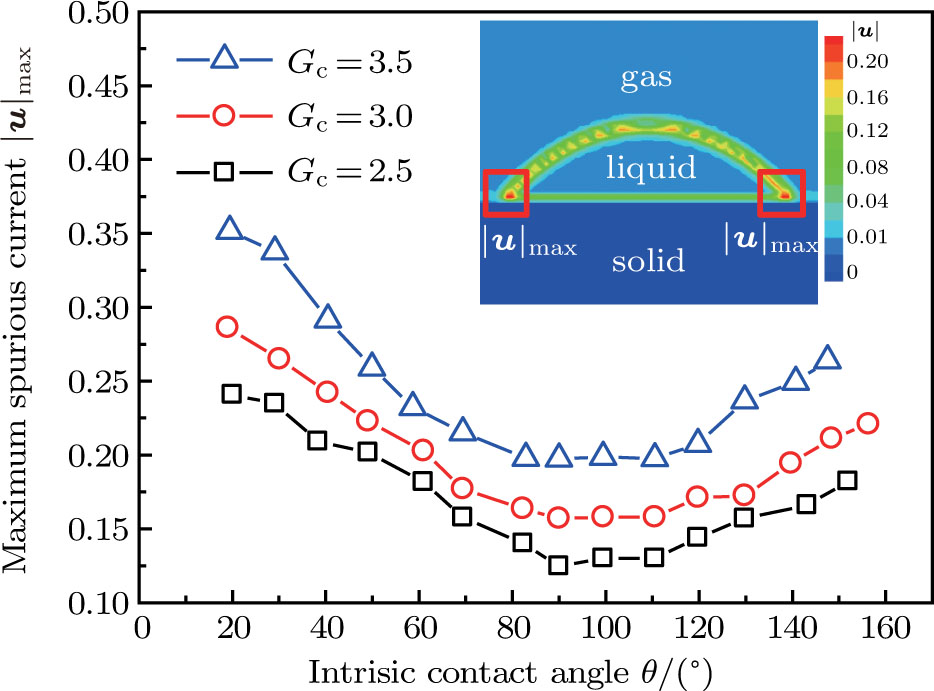
Figure 8 illustrates the maximum spurious currents in the presence of a solid phase as a function of the intrinsic contact angle for three different values of fluid–fluid interaction strengths 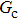 . In the present two-dimensional (2D) study, the maximum spurious current is found to appear at the solid–liquid–gas three-phase contact points as shown in the velocity contour map in Fig. 8. This implies that for the same value of
. In the present two-dimensional (2D) study, the maximum spurious current is found to appear at the solid–liquid–gas three-phase contact points as shown in the velocity contour map in Fig. 8. This implies that for the same value of 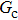 , the maximum spurious current appearing in the solid–liquid–gas system is larger than that in the liquid–gas system. Moreover, it can be seen from Fig. 8 that for a certain
, the maximum spurious current appearing in the solid–liquid–gas system is larger than that in the liquid–gas system. Moreover, it can be seen from Fig. 8 that for a certain 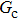 , the intrinsic contact angles within
, the intrinsic contact angles within  produce relatively small values of the spurious current. Note that the intrinsic contact angles in this range correspond to the simulations adopting fluid–solid interaction strengths of
produce relatively small values of the spurious current. Note that the intrinsic contact angles in this range correspond to the simulations adopting fluid–solid interaction strengths of 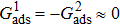 . As the contact angles are regulated to higher or lower degrees by increasing
. As the contact angles are regulated to higher or lower degrees by increasing  and
and 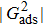 , the spurious current is accordingly elevated, indicating that the spurious current is enlarged by the fluid–solid interaction force. For a certain value of the intrinsic contact angle, the spurious current is apparently enlarged by the increase of
, the spurious current is accordingly elevated, indicating that the spurious current is enlarged by the fluid–solid interaction force. For a certain value of the intrinsic contact angle, the spurious current is apparently enlarged by the increase of  . As discussed previously, the local intense spurious currents may lead to non-convergent computations. The magnitude of
. As discussed previously, the local intense spurious currents may lead to non-convergent computations. The magnitude of 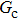 is thus restricted to a lower level for the solid–liquid–gas system than that for the liquid–gas system, owing to the fact that there is higher maximum spurious current appearing in the solid–liquid–gas system. Since
is thus restricted to a lower level for the solid–liquid–gas system than that for the liquid–gas system, owing to the fact that there is higher maximum spurious current appearing in the solid–liquid–gas system. Since 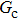 is a dominant parameter responsible for enlarging the liquid–gas density ratios as shown in Figs. 3 and 7, it is evident that the achievable maximum liquid–gas density ratio in the simulations of the solid–liquid–gas system are smaller than that of the liquid–gas system. In the present work, the maximum liquid–gas density ratio obtained from the solid–liquid–gas system is around 600:1.
is a dominant parameter responsible for enlarging the liquid–gas density ratios as shown in Figs. 3 and 7, it is evident that the achievable maximum liquid–gas density ratio in the simulations of the solid–liquid–gas system are smaller than that of the liquid–gas system. In the present work, the maximum liquid–gas density ratio obtained from the solid–liquid–gas system is around 600:1.
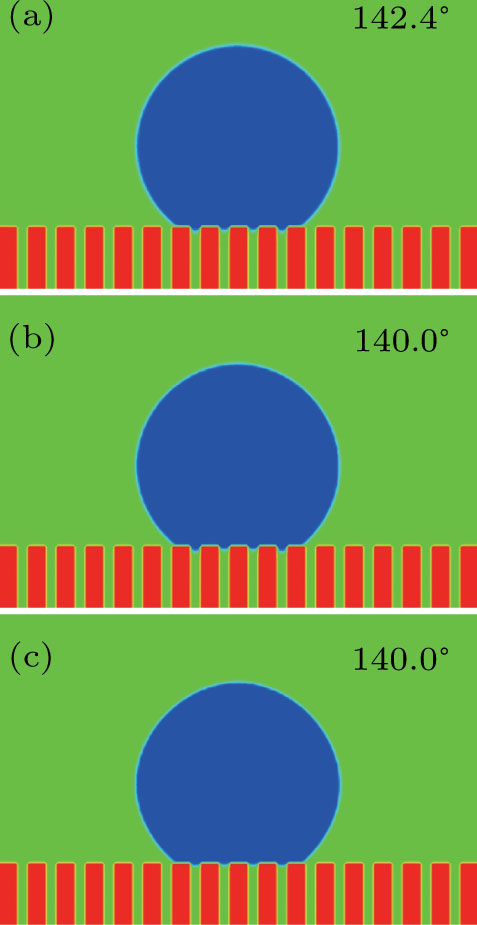
3.4. Apparent contact angles of a droplet on rough solid surfacesLi et al.[48] performed simulations of the apparent contact angles of droplets on rough surfaces by using two types of SCMP pseudopotential LB models. The intrinsic contact angles of the droplets in their LB models were regulated close to 138°. After the steady states of the droplets were achieved, the apparent contact angles were measured and compared with the predictions of Cassie’s law. To further demonstrate the validity of the present MCMP LB model, the wetting behaviors of droplets on rough surfaces are also simulated. The computation domain consists of 150 × 100 lattice units and an initial droplet with a radius of 30 lattice units is placed on the rough surface. As shown in Fig. 9, the rough surface is composed of square pillars. The width, pillar–pillar spacing, and height of the square pillars are selected as w = 6, s = 3, and h = 20 lattice units, respectively. The initial droplet radius and the geometrical configuration of the rough surface are taken to be identical with those used in the study of Li et al.[48] The time step ratio is set to be 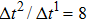 that is identical with those used in the simulations of droplets on a smooth surface in Subsection 3.3. With respect to the three liquid–gas regimes determined by
that is identical with those used in the simulations of droplets on a smooth surface in Subsection 3.3. With respect to the three liquid–gas regimes determined by 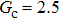 ,
, 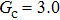 , and
, and 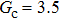 , the fluid–solid interaction strengths are regulated as
, the fluid–solid interaction strengths are regulated as 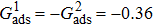 ,
, 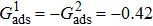 , and
, and 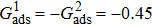 , respectively, to obtain an intrinsic contact angle of 137.7°. After the droplets reach the steady state on the rough surfaces, the apparent contact angles, measured from the simulated droplets shown in Fig. 9, are 142.4°, 140.0°, and 140.0°, respectively. According to Cassie’s law,[49] the apparent contact angle of a droplet sitting on the top of the pillars can be calculated from
, respectively, to obtain an intrinsic contact angle of 137.7°. After the droplets reach the steady state on the rough surfaces, the apparent contact angles, measured from the simulated droplets shown in Fig. 9, are 142.4°, 140.0°, and 140.0°, respectively. According to Cassie’s law,[49] the apparent contact angle of a droplet sitting on the top of the pillars can be calculated from
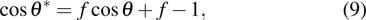 | |
where
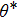
and
θ denote the apparent contact angle and the intrinsic contact angle, respectively and
f is the area fraction of the liquid–solid contact surface with respect to the horizontally projected plane of the droplet base. In the present (2D) study, according to the shape of droplets on the rough surfaces shown in Fig.
9,
f is calculated from
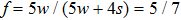
. Substituting the area fraction
f = 5/7 and the intrinsic contact angle
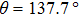
into Eq. (
9), the apparent contact angle is computed to be
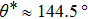
. Thus, the relative errors between the simulation data measured from Fig.
9 and the predictions of Eq. (
9) are all less than 3.2%. In the work of Li
et al.,
[48] the simulated apparent contact angles on the rough surface are all around 146.0°. It can be found that the simulated apparent contact angles in Fig.
9 are also close to the simulation results obtained by Li
et al.
[48] These obtained agreeable results indicate that the proposed MCMP LB model can reasonably describe the wetting phenomena of droplets on rough surfaces in solid–liquid–gas systems with various interaction strengths.
3.5. Dynamics of capillary flowThe above contact angle simulations are all for the static cases. In order to demonstrate the validity of the present MCMP LB model for the simulation of fluid dynamics in the liquid–gas–solid coexisting system, the dynamic process of liquid movement in a capillary tube is simulated. Liquid moves in a capillary tube due to the pressure difference over the curved liquid–gas interface, which is simulated using several types of LB multiphase models, and can be taken as a benchmark for assessing the capability of a multiphase model for the simulation of dynamic problems.[50–52] The position of the moving liquid–gas interface in the capillary tube can be expressed as follows:[52]
where
γ is the surface tension,
θ is the intrinsic contact angle,
r is the width of the capillary tube in the 2D study,
ξ is the real-time position of the liquid–gas interface in the capillary tube,
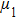
and
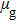
are the dynamic viscosities of the liquid and gas phases, respectively.
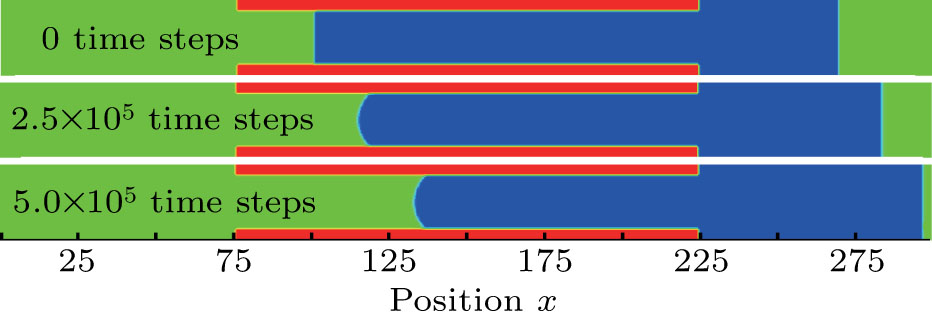
In the present study, the computation domain consists of 300 × 25 lattice units. In the middle portion of the computation domain, namely, 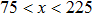 , placed is a horizontal capillary tube with a width of 17 lattice units. The liquid region is initialized at the position of
, placed is a horizontal capillary tube with a width of 17 lattice units. The liquid region is initialized at the position of 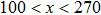 , and the remaining region is filled with the gas phase. Thus, the initial liquid–gas interface position on the left-hand side, ξ, is x = 100 in the computation domain. The simulation parameters, including the time step ratio and interaction strengths, are assigned to be identical with those of Fig. 9. Consequently, according to the simulations of Fig. 9, the intrinsic contact angles are 137.7° for the three liquid–gas regimes distinguished by
, and the remaining region is filled with the gas phase. Thus, the initial liquid–gas interface position on the left-hand side, ξ, is x = 100 in the computation domain. The simulation parameters, including the time step ratio and interaction strengths, are assigned to be identical with those of Fig. 9. Consequently, according to the simulations of Fig. 9, the intrinsic contact angles are 137.7° for the three liquid–gas regimes distinguished by 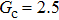 ,
, 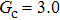 and
and 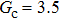 that determine different surface tensions. Figure 10 displays the time evolutions of liquid movement in the capillary tube when the interaction strengths are taken as
that determine different surface tensions. Figure 10 displays the time evolutions of liquid movement in the capillary tube when the interaction strengths are taken as 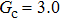 and
and 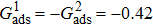 . It is observed that after the calculation is started, the initial plane liquid–gas interface becomes curved, and the liquid moves in the capillary tube gradually towards the right-hand side.
. It is observed that after the calculation is started, the initial plane liquid–gas interface becomes curved, and the liquid moves in the capillary tube gradually towards the right-hand side.
Since the relaxation times of the two components are adopted as 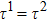 , the dynamic viscosities of the liquid and gas phases are identical, namely,
, the dynamic viscosities of the liquid and gas phases are identical, namely, 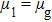 . Therefore, equation (10) can be rewritten for the LB simulations as
. Therefore, equation (10) can be rewritten for the LB simulations as
where
M is a parameter and defined as
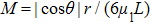
. As described in Subsection
3.4, with respect to the three liquid–gas regimes determined by
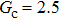
,
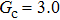
, and
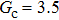
, the contact angles are regulated to be identical. Therefore,
M in Eq. (
11) is a constant in the simulations of the three liquid–gas regimes. It can be seen from Eq. (
11) that the variation of the liquid–gas interface position,
ξ, with respect to simulation time,
t, is linear. The slope of the
ξ–
t line is proportional to the surface tension,
γ. In the present MCMP LB model, the surface tension can be calculated through Laplace’s law by measuring the pressure difference across the liquid–gas interface and the radius reciprocal of the spherical droplets. It is obtained that the surface tensions of the three liquid–gas regimes are
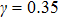
,
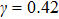
, and
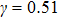
for
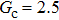
,
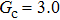
, and
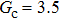
, respectively, showing that the surface tension,
γ, increases with the fluid–fluid interaction strength,
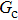
.
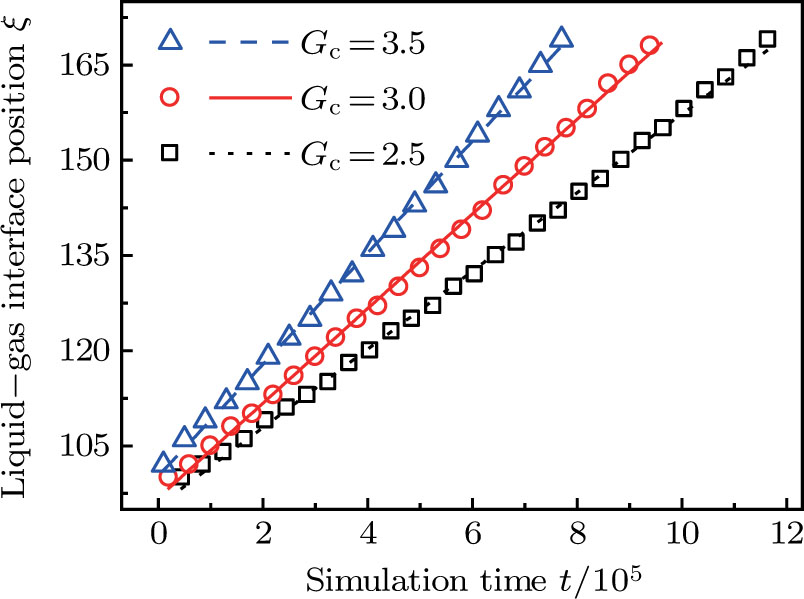
Figure 11 shows the plots of the simulated position of the curved liquid–gas interface in the capillary tube versus simulation time for different values of fluid–fluid interaction strengths, 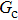 . The symbols in Fig. 11 represent the simulation results, and the lines are the linear fitting plots of the symbols. Note that the linear relation between the liquid–gas interface position and simulation time is observed, which is identical with the analytical prediction of Eq. (11). In addition, it is found that the slope of the ξ–t line increases with the increase of fluid–fluid interaction strength,
. The symbols in Fig. 11 represent the simulation results, and the lines are the linear fitting plots of the symbols. Note that the linear relation between the liquid–gas interface position and simulation time is observed, which is identical with the analytical prediction of Eq. (11). In addition, it is found that the slope of the ξ–t line increases with the increase of fluid–fluid interaction strength, 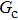 . The slopes can be determined from the linear fitting plots in Fig. 11, and obtained as
. The slopes can be determined from the linear fitting plots in Fig. 11, and obtained as 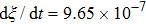 ,
, 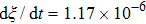 , and
, and 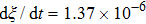 for
for  (
(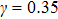 ),
), 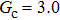 (
(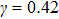 ), and
), and 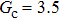 (
(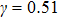 ), respectively. Accordingly, the slope of the ξ–t line is approximately proportional to the surface tension, which is identical with the analytical prediction by Eq. (10). Liu et al.[52] performed the simulation of the capillary flow by using a color-fluid multiphase LB model, and also obtained the linear relationship between the liquid–gas interface position, ξ, and time, t. These agreeable results demonstrate the capability of the present MCMP LB model when dealing with the dynamic problems in the liquid–gas–solid systems.
), respectively. Accordingly, the slope of the ξ–t line is approximately proportional to the surface tension, which is identical with the analytical prediction by Eq. (10). Liu et al.[52] performed the simulation of the capillary flow by using a color-fluid multiphase LB model, and also obtained the linear relationship between the liquid–gas interface position, ξ, and time, t. These agreeable results demonstrate the capability of the present MCMP LB model when dealing with the dynamic problems in the liquid–gas–solid systems.
4. ConclusionsIn the present study, a modified multicomponent multiphase (MCMP) pseudopotential lattice Boltzmann (LB) model with large liquid–gas density ratios is proposed. Two layers of neighboring nodes are employed to calculate the fluid–fluid cohesion force, which can elevate the isotropy order of the interaction force and effectively reduce the spurious current. Different time steps for the two fluid components, with a large pseudo-particle mass contrast, are implemented in the proposed MCMP LB model. It is found that the liquid–gas density ratio can be elevated by increasing 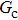 at a fixed
at a fixed 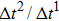 . For a given
. For a given 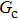 , the liquid–gas density ratio increases as
, the liquid–gas density ratio increases as 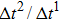 becomes larger before it approaches to a relatively stable value. For the liquid–gas flow system without solid phase, the largest liquid–gas density ratio is observed to be
becomes larger before it approaches to a relatively stable value. For the liquid–gas flow system without solid phase, the largest liquid–gas density ratio is observed to be 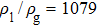 under the conditions of
under the conditions of  and
and  .
.
The maximum spurious current appears at the liquid–gas interface for the liquid–gas system and at the solid–liquid–gas three-phase contact points for the flow system in the presence of a solid phase. The maximum spurious current is found to be obviously elevated by increasing  , but weakly affected by
, but weakly affected by 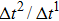 . Moreover, the magnitudes of the fluid–solid interaction strengths, namely
. Moreover, the magnitudes of the fluid–solid interaction strengths, namely 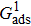 and
and 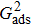 , have less effect on the liquid–gas density ratio, but influence the spurious current clearly. Accordingly, the applicable
, have less effect on the liquid–gas density ratio, but influence the spurious current clearly. Accordingly, the applicable 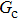 value for the solid–liquid–gas system is smaller than that for the liquid–gas system, which hinders the liquid–gas density ratio from being enlarged to a high level in the presence of solid phase. As a result, the achievable maximum liquid–gas density ratio is smaller than that obtained from fluid flows in the absence of a solid phase.
value for the solid–liquid–gas system is smaller than that for the liquid–gas system, which hinders the liquid–gas density ratio from being enlarged to a high level in the presence of solid phase. As a result, the achievable maximum liquid–gas density ratio is smaller than that obtained from fluid flows in the absence of a solid phase.
Different contact angles of droplets on both smooth and rough solid surfaces are simulated by using the proposed MCMP LB model. The different intrinsic contact angles are obtained by adjusting the interaction strengths. An empirical formula of Young’s equation containing LB interaction strengths is proposed to predict the intrinsic contact angles. The intrinsic contact angles obtained from the simulations and calculated from the suggested LB Young’s equation are in good agreement with each other. With the droplets sitting on the tops of the pillars of a rough surface, the simulated apparent contact angles with various interaction strengths accord well with the predictions of Cassie’s law. Moreover, the dynamic process of liquid movement in a capillary tube is simulated. Under the condition of the liquid and gas phases having an identical dynamic viscosity, the linear relation between the liquid–gas interface position in the capillary tube and simulation time is observed, and the slope of the linear line is approximately proportional to the surface tension. These simulation results of the liquid movement in a capillary tube are consistent with the analytical predictions. The simulations of the static and dynamic problems show that the proposed MCMP LB model is capable of reasonably simulating the wetting phenomena in the solid–liquid–gas coexisting systems with large liquid–gas density ratios.