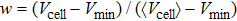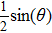Since Bernal,^[1] random granular packing has been used as a model system to simulate the structures of liquids and glasses.^[2–4] The analogy with glassy system is not restricted to structure. Granular packing under tapping has shown slow compaction dynamics which is very similar to thermal glassy systems.^[5–8] Later on, the random granular packing study has mainly focused on random close packing (RCP),^[9,10] which is considered to be closely related to glass transition. The so-called random loose packing (RLP) density,^[11] in which the minimum packing density, a frictional packing, can maintain mechanical stability, has received less attention.^[12] Unlike random close packing, which has been normally found to have a packing fraction close to 0.64, the packing density for RLP has been less well defined. In simulation it was determined to be 0.608±0.006.^[13] However, the experimentally obtained values were in a wide range of 0.56–0.60.^[11] Therefore, a fundamental question would be whether RLP is well defined and potentially associated with a phase transition^[14] similar to RCP. However, since there is no attractive interaction present in the system, very loose packing structures like diffusion-limited-like aggregates cannot be formed.^[15] Therefore, it is natural that indeed a lower bound density should exist.

The RLP density heavily depends on the specific protocol that is produced. Many previous studies including sequential deposition,^[16] tapping,^[17] freeze-thaw cycling,^[18] were used to produce the RLP state. However, these previous methods either do not consider the influence of gravity effect or only partially remove it. As gravity exists, structure is not formed isotropically and therefore gravity force might potentially induce anisotropic effect in the system. This could potentially weaken the description of the RLP state as a thermodynamic uniform steady state as envisioned in previous studies. Additionally, the presence of gravity could destabilize the marginally mechanical stable loose packing structure and therefore conceal the ultimate RLP state experimentally attainable.^[11] One of the drawbacks in previous studies of RLP is that the investigation has been mainly carried out using macroscopic measurements by focusing on the loosest packing density achievable without detailed microscopic structural analysis on the packing prepared.

In our current study, we produce a random loose granular packing under isotropic external compression without gravity and investigate its microscopic structure. To achieve this goal, we design a specialized apparatus where a balloon is used for creating the spherical confinement to provide an isotropic compressional force and also minimize gravitational effect by mixing the density-matched liquids with granular particles inside the balloon. Subsequently, by medical CT scan, we obtain the three-dimensional inner structure information of the packing structure. We also carry out a detailed microscopic structural analysis of the structure obtained and believe that the microscopic structure we obtained will lead to a great insight into the understanding of RLP.

The main part of the apparatus was an acrylic cubic cell with a side length of 20 cm. To pump or inject water with a controllable flow rate, a pump was connected to the bottom of cell side plate through a three-way valve. A rubber O-ring was mounted on a circular groove in the upper plane to maintain the seal of the cell. The lid was fixed on the upper plane by pressing over the O-ring with plastic screws (to avoid any potential artifacts induced in the tomography images due to the presence of strongly x-ray absorbing materials). One end of a tube was connected with a balloon and the other end of the tube is kept outside the container. The scheme of the apparatus is shown in Fig. 1(a).

Fig. 1.

	Figure Option ViewDownloadNew Window
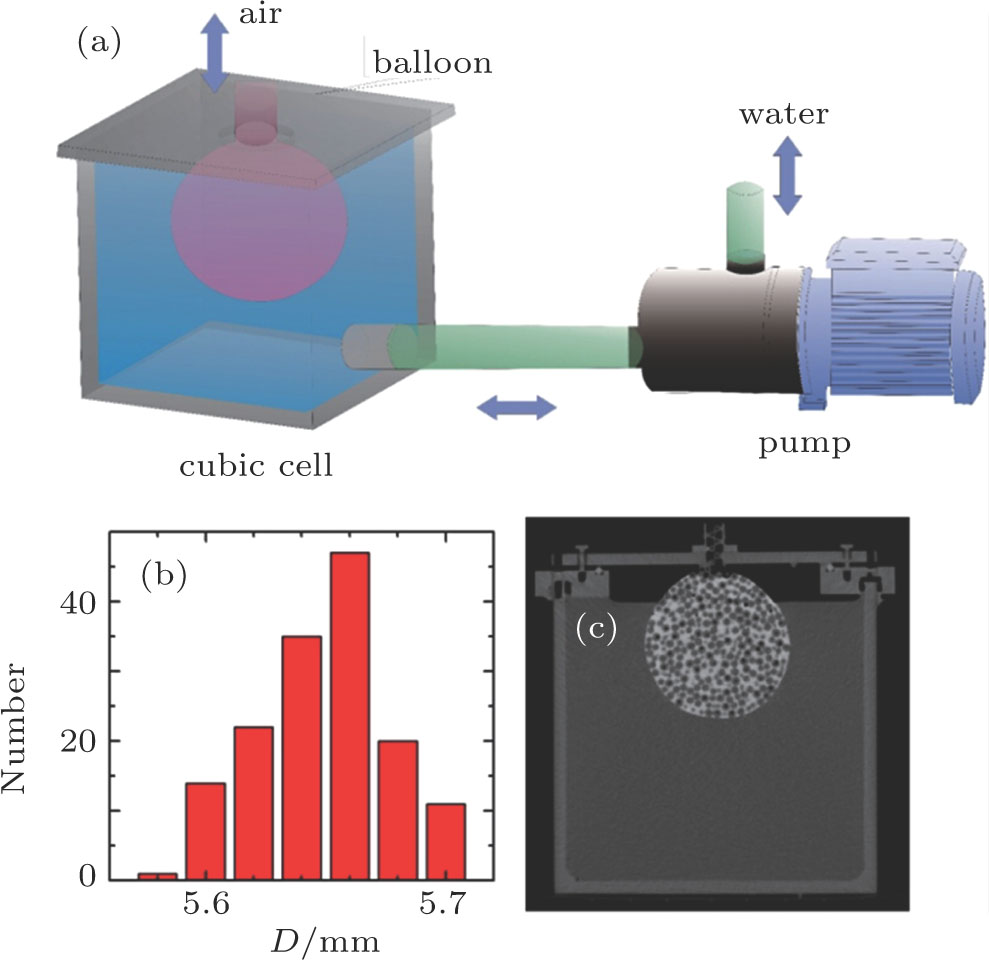	Fig. 1. (color online) (a) Scheme of the experimental apparatus, (b) number distribution of particle diameter, and (c) one tomogram scan of the packing system.

The granular particles used in the experiment were ABS spherical particles with mean diameter of 5.65(2) mm. The sizes of 50 randomly picked particles were measured by caliper. Each particle was measured from three orthogonal directions. The distribution of the 150 measurements is shown in Fig. 1(b). The friction coefficient μ of the particles was measured to be about 0.38.

To minimize the gravity effect, a NaCl solution was prepared with a density of 1.044 g/ml to match the density of particles in the balloon. KI was added to the NaCl solution as the contrast agent to increase the absorption contrast between the particles and liquid for x-rays. The optimized mixture is a solution with 8.8-g/L NaCl and 32.5-g/L KI.

At the beginning of the experiment, the cell was filled with water. After fixing the lid to the upper plate, we pumped water from the container with a flow rate of 117 ml/s so that the balloon began to swell and stopped the pumping when the balloon diameter increased to 14 cm. Spherical particles were fed into the balloon. The results of the image processing analysis indicated that the exact number of particles was 2962. Then the density-matching liquid was poured into the balloon to form a suspension. After the cell was set aside to settle for several minutes, we injected water into the cell with a flow rate of 23 ml/s and used a pipe to drain the NaCl solution from the balloon. The balloon radius began to shrink at a speed of 0.05 cm/s. We stopped injecting water when the particles reached a steady state without further contraction. The final diameter of the balloon was around 10 cm and the surface of the balloon was subjected to a pressure of about 20 kPa.

After we prepared the packing, the whole device was scanned by medical CT scanner (SOMATOM Perspective, Siemens, Germany) with a spatial resolution of 0.6 mm.^[19] Thus we obtained the three-dimensional information about the packing. The x-ray micro-tomography has been a very powerful tool to study the packing structures of granular materials.^[20–22] Figure 1(c) shows the result of one tomogram scan.

To analyze the three-dimensional structure of the packing, we performed a similar imaging processing analysis of the packing structure following previous studies which include imaging binarization and imaging segmentation procedures.^[23] We obtained the packing geometric information including each particle centroid coordinate r, the diameter D, the volume V, and the local Voronoi cell volume 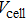. The errors of particle D and V introduced by the binarization threshold were corrected by comparing the ratio of the mean diameter value from image processing with the mean value from the hand measurements.

To reduce the influence of the boundary, we only study the particles that are at least 1D away from the boundary, where D is the mean diameter of the particles. Thus 1731 particles are involved in the structural analysis. Subsequently we analyze local structure information of the system such as distributions of local free volume, neighbor number, coordination number, etc.^[24,25] Furthermore, we investigate the structural spatial correlation by standard g₂ function and higher-order structural correlation function such as angular correlation distribution.

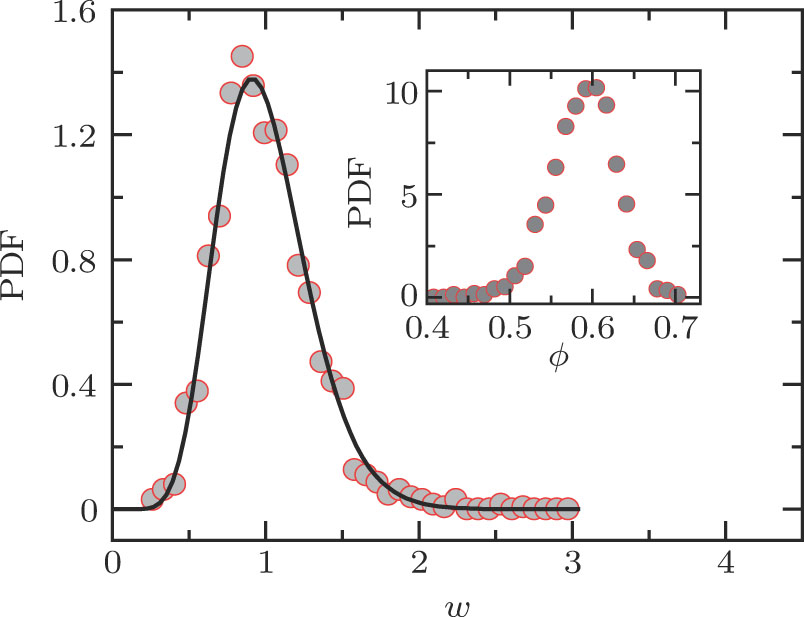
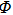
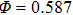
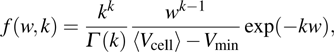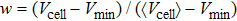
The volume fraction is obtained by using the Voronoi tessellation as . The global volume fraction obtained is , which is close to the value in a range from 0.56 to 0.6 identified from previous studies,^[10,11] which suggests that our system is a well-prepared random loose packing. Furthermore, we obtain the distribution of the local volume fraction , which yields microscopic structural information as shown in the inset of Fig. 2. From previous experimental and simulation studies, the local volume distribution at statistical equilibrium state will follow the shifted and rescaled k–Gamma distribution.^[26] This k–Gamma distribution is defined as

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (color online) Distribution of the Voronoi volume. The inset shows the local volume fraction distribution. w is defined as and ϕ is the local volume fraction. PDF is short for probability distribution function.

Since the gravity effect has been effectively eliminated during the packing preparation, the system should behave with no anisotropic effect. 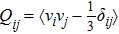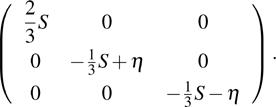It can be testified by analyzing whether there exists a preferential Voronoi cell orientation due to the presence of a potential nematic order.^[27,28] Thus, a unit vector v^α pointing along the long axis of the Voronoi cell α can be defined and we define the global nematic order parameter in the tensor form: where v_i is the i-th component of the unit vector v^α, Q_ij can be diagonalized as

For an isotropic system, the values of S and η should be zero. S and η calculated in our system are 0.71 × 10⁻² and 0.60 × 10⁻² respectively. To test whether these small values are due to a true nematic order or statistical fluctuation simply associated with a finite number effect, we generate 1731 (the number the same as that of our Voronoi cells) randomly (uniformly) orientated unit vector and calculate the corresponding nematic order parameter. The corresponding values of S and η are 1.95 × 10⁻² and 0.69 × 10⁻², respectively, which suggests that our packing is very isotropic.

We also calculate the local neighbor number N and contact number Z, which are quantities yielding local topological information about the system. The neighbor number N of our system is obtained by the Delaunay triangulation method while the contact number Z is acquired by contact number scaling function (CNS function).^[28,29] The distributions of N and Z are shown in Fig. 3 and the corresponding CNS function fitting in obtaining Z is shown in the inset of Fig. 3 with a threshold radial distance of 1.027D, where D is the mean diameter of particles. The contact number Z of our RLP system is 5.73, which is close to that of similar packing density prepared under gravity.^[29] We believe that the potential reason why our contact number is fairly close to 6 suggests that the isotropic RLP prepared might be still fairly close to isostaticity due to its rather isotropic extent which is not close to the shear jamming limit.^[30] This could suggest that the limit we obtained is the isotropic lower limit of the RLP instead of anisotropic one.

Fig. 3.

	Figure Option ViewDownloadNew Window
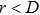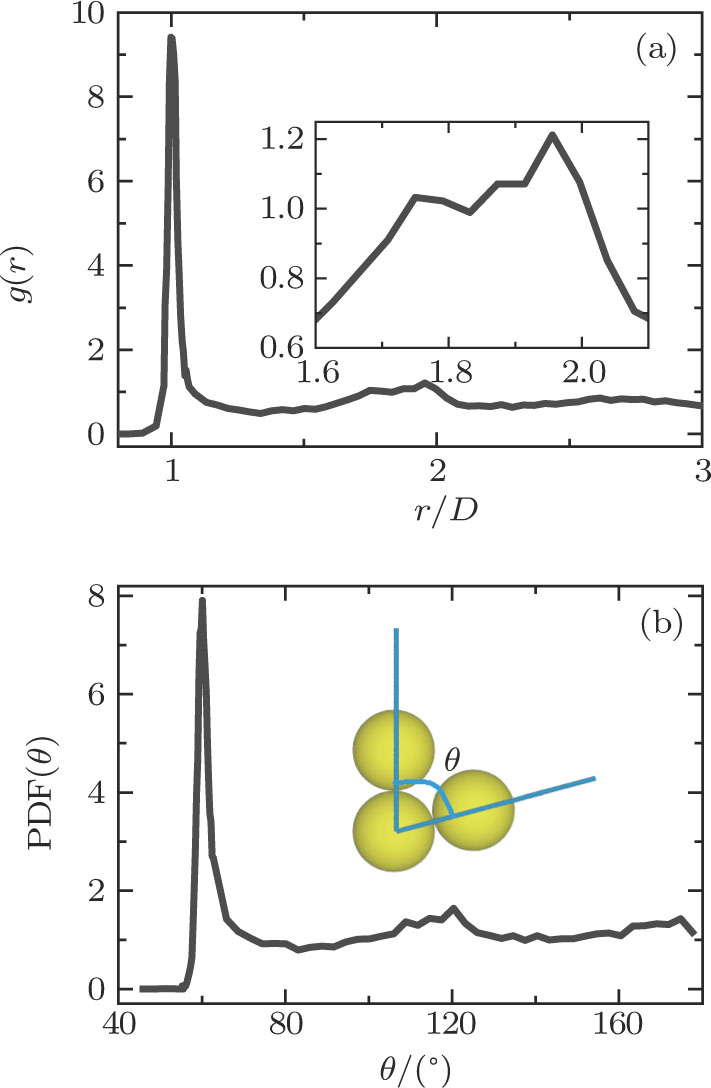
	Fig. 3. (color online) Distributions of neighbor number N and contact number Z. Error function in the inset is the best fitting with the data when ,[29] where D is the mean diameter of particles.

We further characterize the local structure by radial distribution function. The radial distribution function (g₂ function) is the distribution of probability to find the center of another particle at different distances, which contains the long-range structural correlation information in the system.^[29] Clearly, there is a split in the second peak of our packing, which is a characteristic of random packings of spheres. The detail of the second peak in g₂ function is magnified and is shown in the inset of Fig. 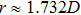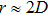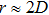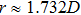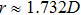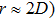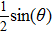4(a). The second peak splits into two subpeaks at and where D is the mean diameter of particles and the subpeak at is more significant than the one at , the positions of peaks are consistent with the results of previous studies.^[29,31] The first subpeak (at ) is due to the presence of triangles with adjacent sides and face-sharing tetrahedra, and the second subpeak (at results from linear chain structure of three particles.^[20] This emergence of an increasing organization in the packing structure suggests that RLP might potentially be associated with the growth of certain order.^[20,29,31] This finding is consistent with the existence of some local favored structures, which suggests that the high-order structure correlation characterization is of great importance. Thus the g₂ function is not sufficient to provide necessary information since it is by nature a two-body correlation function. Therefore we introduce an angular correlation function which is a three-body structural correlation function characterizing the probability distribution function (PDF) of the angle θ between two neighbor particles and the center particle. The PDF is scaled by and is shown in Fig. 4(b). Two peaks appear at 60° and 120°, which is consistent with the existence of equilateral triangle of particles and the diamond structure respectively suggested above.^[5]

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (color online) (a) Radial distribution function (g2 function), where the inset shows the magnification of the second peak in g2 function. (b) Angular correlation function. The PDF is scaled by .

Overall, our study provides a very clean system to study the RLP structure without the interference of gravity or anisotropic effect. Therefore, it is expected that our results provide useful information about the nature of RLP and in general about granular physics.^[32–35] From the above observations on the weak angular correlation and short correlation length of the glass order, we find that our study strongly suggests that the RLP state corresponds to the state when the system just enters the energy landscape, therefore the RLP state should be closely related to the structure of glassy system close to the MCT transition and bears great thermodynamic significance. The RLP density we have obtained is higher than those of previous studies, which hints the possible anisotropic effects induced by either gravity or friction in previous studies.