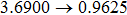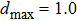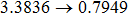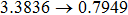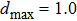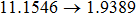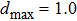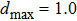† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11571223 and U1433104).
The improved element-free Galerkin (IEFG) method of elasticity is used to solve the topology optimization problems. In this method, the improved moving least-squares approximation is used to form the shape function. In a topology optimization process, the entire structure volume is considered as the constraint. From the solid isotropic microstructures with penalization, we select relative node density as a design variable. Then we choose the minimization of compliance to be an objective function, and compute its sensitivity with the adjoint method. The IEFG method in this paper can overcome the disadvantages of the singular matrices that sometimes appear in conventional element-free Galerkin (EFG) method. The central processing unit (CPU) time of each example is given to show that the IEFG method is more efficient than the EFG method under the same precision, and the advantage that the IEFG method does not form singular matrices is also shown.
Structural optimization design occupies a significant position in science and engineering. As a challenging topic in structural optimization, the topology optimization meets the requirements by redistributing the material under the design constraints.[1]
Bendsoe presented the homogenization method.[1] Inspired by the homogenization method, Bendsoe presented the variable density method.[2] Then he presented the solid isotropic microstructures with penalization (SIMP).[3,4] The 99-line topology optimization code along with the web-based program of Sigmund has a large effect on the promotion of SIMP.[5,6] In 1993, the evolutionary structural optimization was presented based on a discrete variable.[7] In addition, some other new methods, including bubble method, level set method and topology description function, were presented.[8,9]
The finite element method (FEM) is an important method of numerically analyzing the topology optimization of structures. In the topology optimization based on FEM, the regularization methods, including the filtering methods and the projection methods, are proposed to alleviate the gray transition problem.[10,11] However, FEM may have problems like mesh distortion and grid moving when solving large deformation problems, therefore it needs to use re-meshing technique when the computational accuracy cannot be reached.[12,13] For the topology optimization of structures based on large deformation theory, the re-meshing technique in FEM is necessary.
The meshless method, especially the element-free Galerkin (EFG) method, is a kind of challenging numerical method in science and engineering. The EFG method has been applied to many fields, such as elasticity problems of different dimensions, elastodynamics, elastoplasticity, elastic large deformation, plate, shell, fracture, and crack expanding problems.[14,15] It constructs the discrete equations on selected nodes in the problem domain and its boundary. Then it can overcome the mesh dependence and omit the re-meshing process in FEM, and its advantages has been shown.[16,17] The EFG method has been applied to the topology optimization problems.[18,19]
The EFG method is based on the moving least-square (MLS) approximation, which has been proved with high accuracy to obtain the functions.[20] But the final algebraic equation system of the MLS approximation is sometimes ill-conditioned. The shape function of the MLS approximation is more complicated than the one of FEM, the computational efficiency of the EFG method is much lower than FEM, it cannot even obtain a solution sometimes. Then it is important to avoid ill-conditioned or singular algebraic equation systems, and improve the computational efficiency of the EFG method.
The improved MLS (IMLS) approximation was proposed by Cheng Y M and Chen M J to overcome the disadvantages of the MLS approximation method and the corresponding meshless method.[21] The IMLS approximation replaces the normal algebraic basis functions with the weighted orthogonal ones to avoid ill-conditioned equations. In the IMLS approximation, the inverse matrix will not be needed any more, and the solutions can be obtained directly, which results in high computational efficiency. When the node distribution is the same, the efficiency of the IMLS approximation is higher than that of the MLS approximation, which is because IMLS approximation requires fewer nodes in the influence or support domain.[21]
Based on the IMLS approximation, the improved element-free Galerkin (IEFG) method was presented for many problems, such as elasticity, fracture,[22] elastodynamics,[23] transient heat conduction,[24] viscoelasticity,[25] wave equation,[26] and large deformation.[27] Compared with the EFG method, the IEFG method do not form ill-conditioned or singular equations, then the computational efficiency is higher, because the IMLS approximation is used to obtain the shape function. Now the IEFG method has no longer been used for the topology optimization.
Based on the IMLS approximation, the IEFG method for the topology optimization is presented in this paper, and the corresponding formulae are given. The IEFG method in this paper can overcome the disadvantage of the singular matrices that sometimes appear in the EFG method. The CPU time of each example is given to show that the IEFG method is more efficient than the EFG method under the same precision. And it is discussed that when singular matrices appear in the EFG method, the IEFG method in this paper can obtain a correct solution.
For function 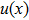
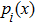
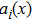
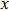
We can make the basis functions orthogonal based on Gram-Schmidt orthogonalization. For
The corresponding local approximation within the neighborhood of 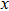
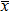
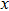
Let
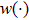
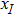
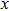

From
When 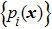
By substituting Eq. (
Thus, when equation (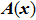
From Eq. (
With the same node distribution, the efficiency of the IMLS approximation is higher than that of the MLS. As the basis function 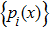
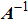
From Eq. (
In this section, the discrete equations are obtained based on the functional variation, which has the same form as the Galerkin weak form, and are imposed on by the displacement boundary conditions through the penalty method.[28,29]
The equilibrium equation of two-dimensional elasticity is
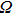
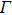
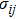
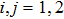
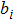
The corresponding geometric equation is
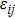
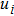
The constitutive equation is
The boundary conditions are
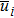
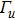
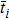
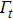
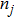

The penalty method is used to add the displacement boundary condition to the equation, then the functional of an elasticity problem is
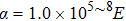
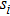
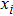
Discretizing the solution domain with M nodes and using the IMLS approximation, we have the approximation function of the displacement as
From 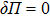
According to the basic idea of variable density method, we assume that the range of the relative density of the material is between 0 and 1, and choose the relative node density as the design variable. From the SIMP, which is common in variable density method, we obtain the mathematical model of material as.[2–4]
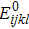
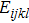
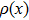
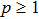
As the relative density is chosen to be design variable, we construct the relative density field with the shape function of the IMLS approximation as
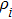

Considering the relative density as the design variable, the volume of structure as the constraint, and the minimization of compliance as the objective function of optimization, the model of topology optimization with the IEFG method is[5,6]


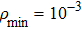
Sensitivity of objective compliance will be obtained using the adjoint method.[30]
From Eq. (
From Eq. (
From Eq. (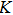
We choose three typical problems as examples to display the correctness and the advantage of IEFG method for topology optimization problems.
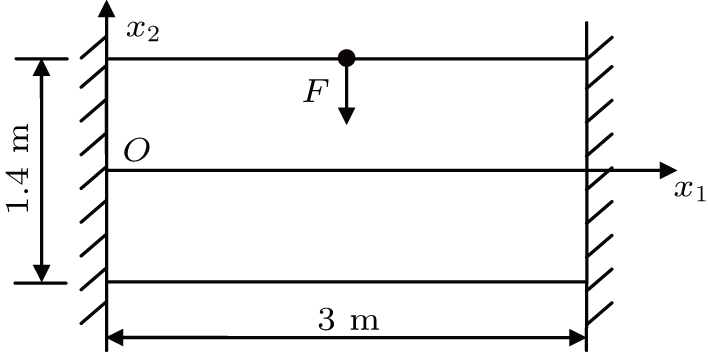
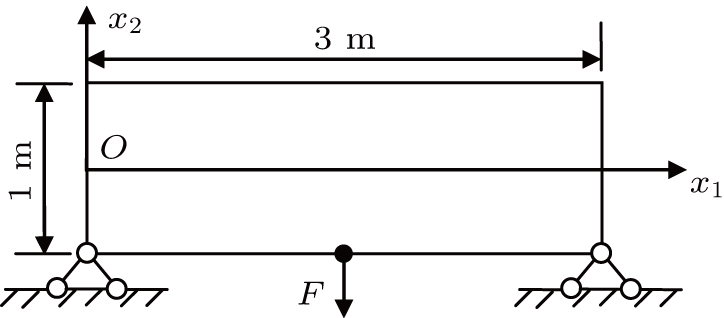
As shown in Fig. 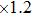
Based on the EFG method and IEFG method, 41 × 13 uniformly distributed nodes and 16 × 5 integral cells are used. 4 × 4 points are selected for Gauss integral on a cell. The scaling parameter of the influence domain of nodes is 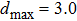
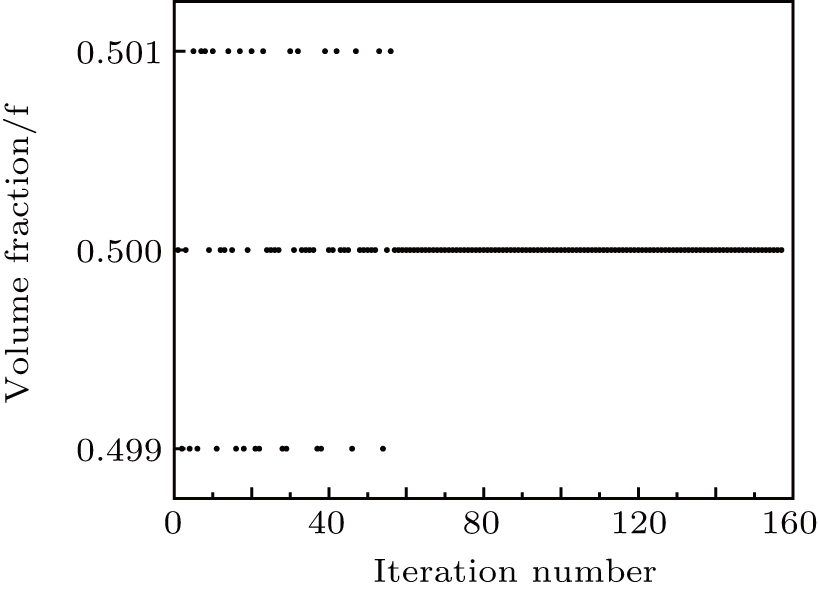
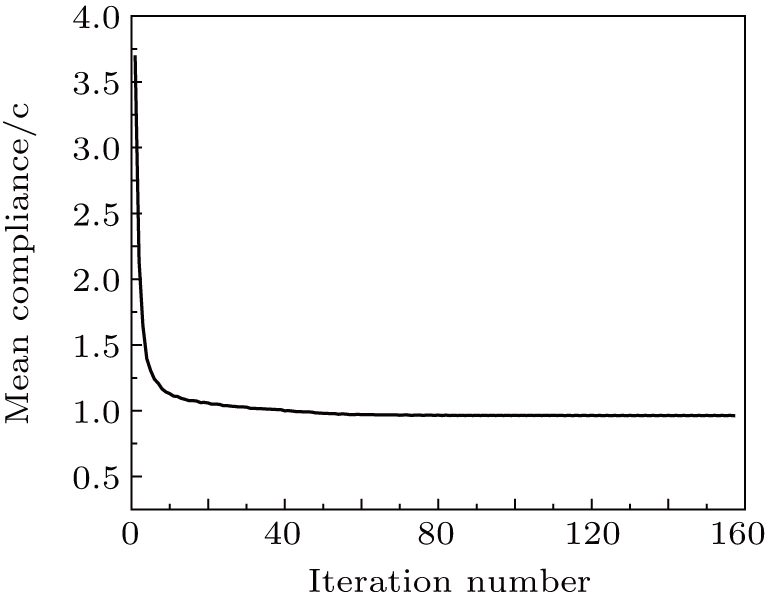
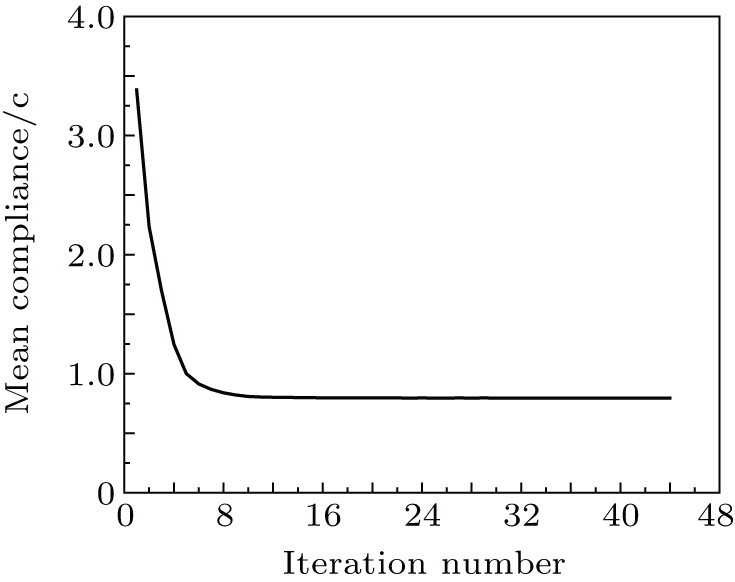
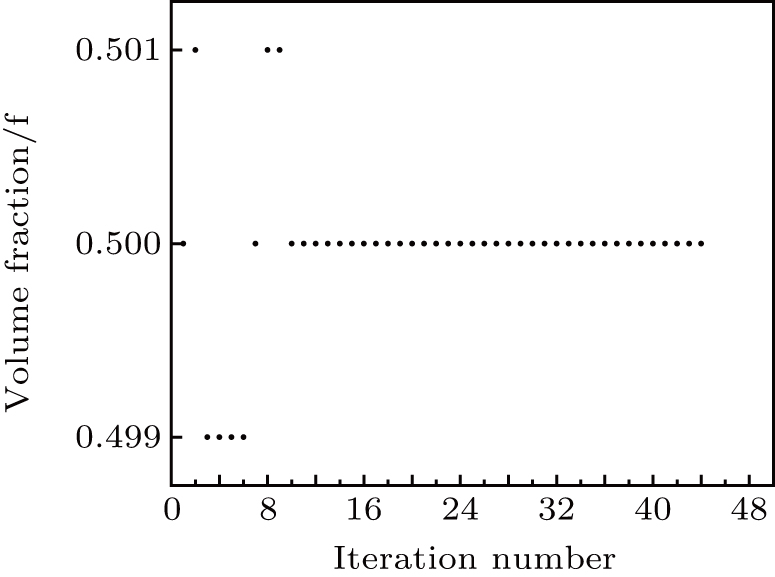
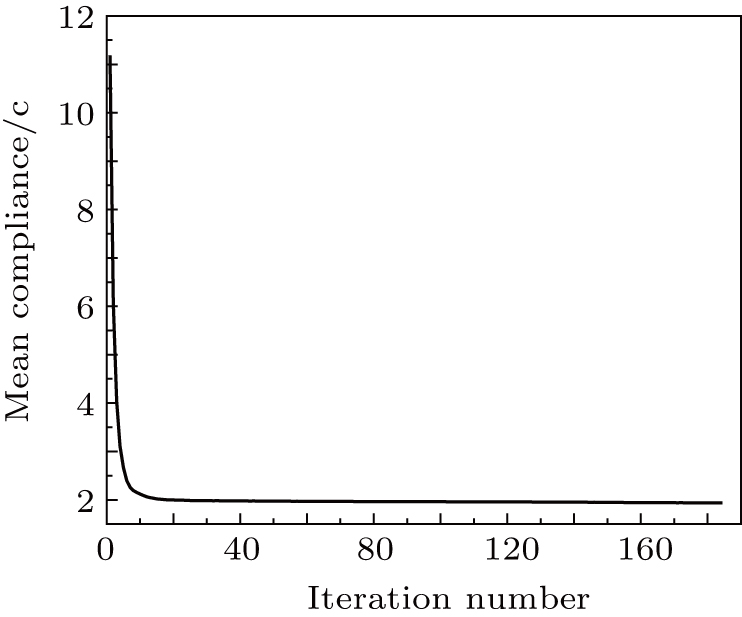
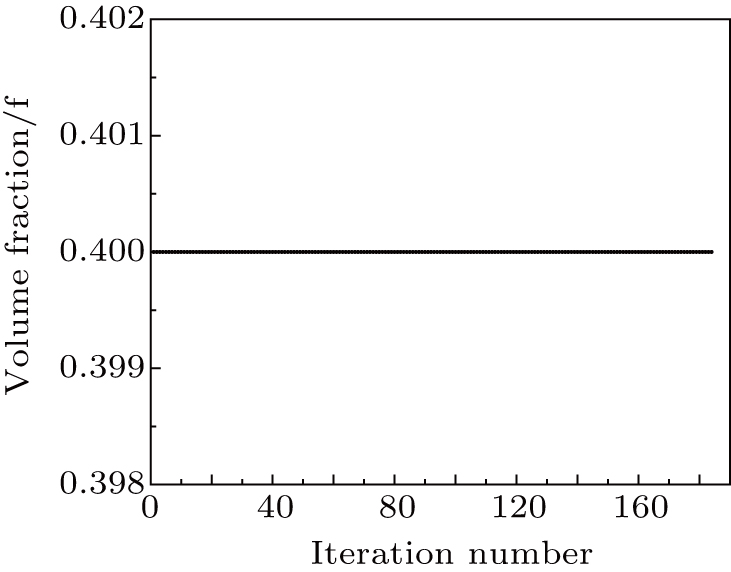
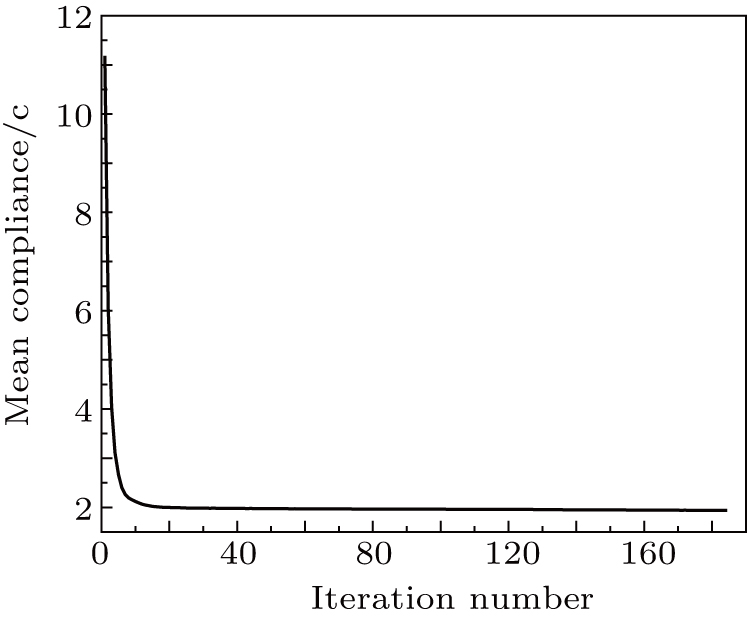
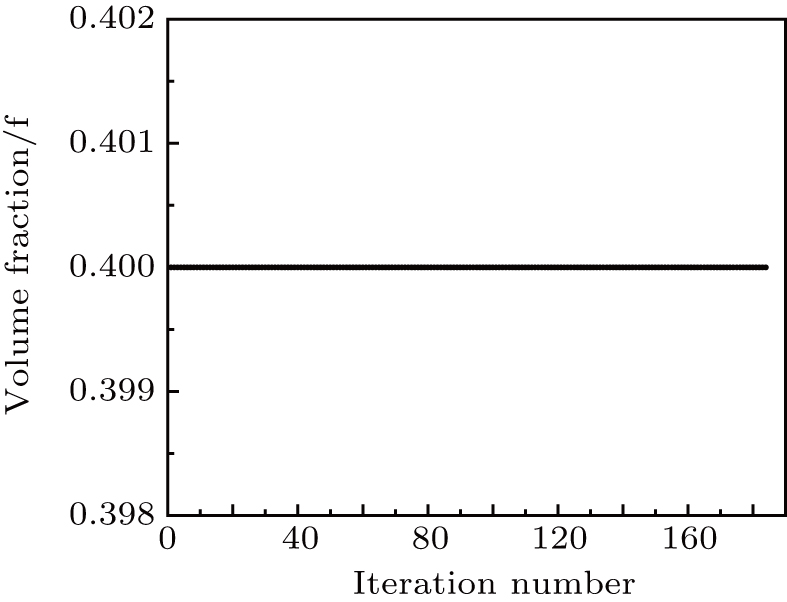
The results of topology optimization using different methods, are presented in Figs.
Figures
Another advantage of the IEFG method over the EFG method is that it never forms a singular matrix in the IMLS approximation. For example, if 
As shown in Fig.
Based on the EFG method and IEFG method, 31 × 15 uniformly distributed nodes and 15 × 4 integral cells are used in the design domain. 4 × 4 points are selected for Gauss integral on a cell. The scaling parameter of the influence domain of nodes is 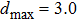
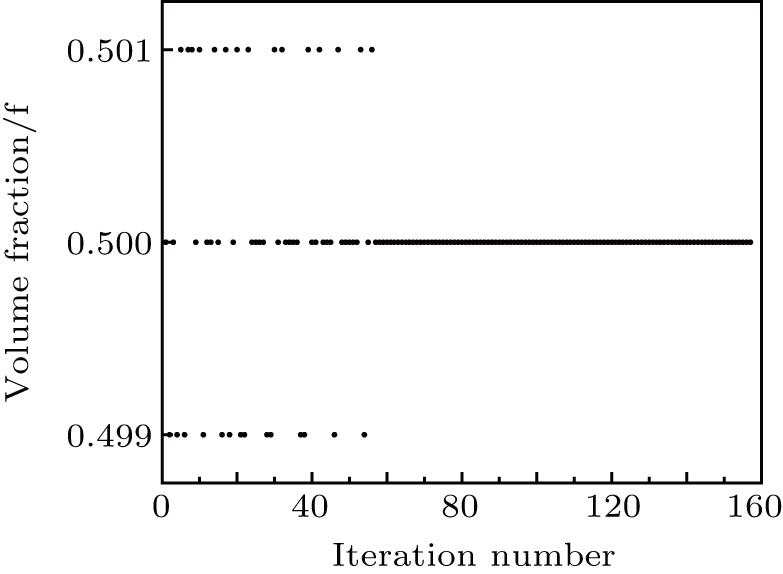
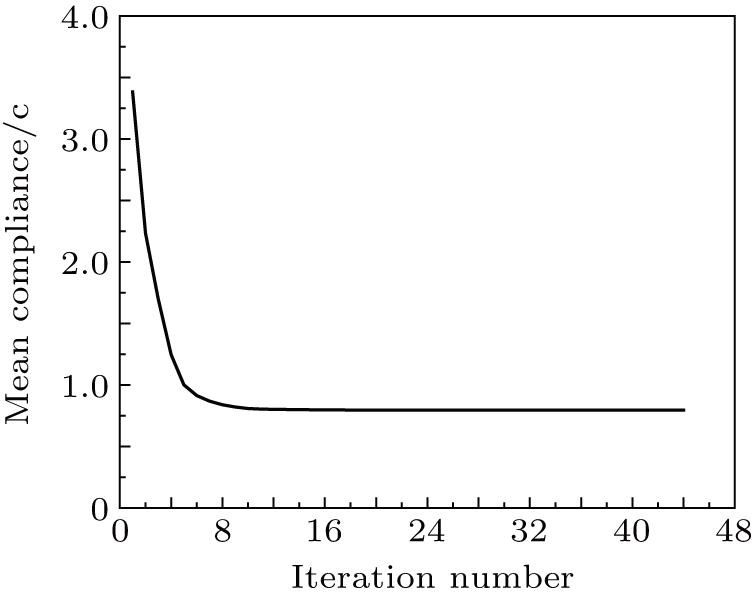
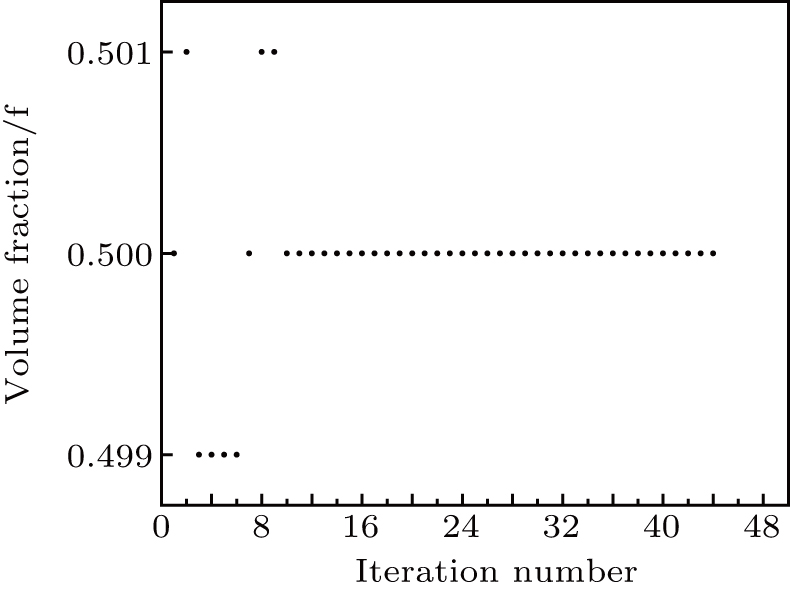
The results of topology optimization using different methods, are presented in Figs.
Similarly, if 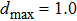
As shown in Fig.
Based on the EFG method and IEFG method, 31 × 11 uniformly distributed nodes and 15 × 5 integral cells are used in the design domain. 4 × 4 points are selected for Gaussian integral on a cell. The scaling parameter of the influence domain of nodes is 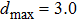
The results of topology optimization using different methods are presented in Figs.
Similarly, if 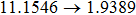
In this paper, the IEFG method of dealing with the topology optimization problem of structures is presented. By analyzing three problems as example, the advantages of the IEFG method of optimizing the topology of structure are shown.
The optimized structures are clear with definite boundaries and the checkerboard phenomenon disappears.
Furthermore, the topology optimization using the IEFG method is much more efficient than the EFG method. Moreover, the IEFG method can overcome the disadvantages of singular matrices in the EFG method.