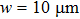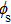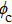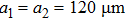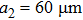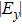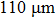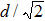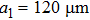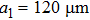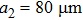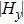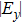Guided mode resonance in planar metamaterials consisting of two ring resonators with different sizes
Centre for THz Research, China Jiliang University, Hangzhou 310018, China
† Corresponding author. E-mail:
hongzhi@cjlu.edu.cn
1. IntroductionGuided mode resonance (GMR) in a dielectric grating waveguide was firstly proposed and used as a filter in 1990.[1,2] Since then, GMRs have been widely investigated and realized with either dielectric or metallic gratings in both optical and terahertz regions.[3–8] The spectral width of the resonance can be controlled and even dramatically suppressed by changing the grating modulation depth.[8–10] Nevertheless, the functionality and flexibility of the conventional grating based GMRs are limited due to their simple structures. In the meanwhile, metamaterials (MMs) have attracted considerable interest in the past few decades due to its potential applications in various devices and high sensitive label-free sensing from microwave, terahertz, to optical frequencies. However, the quality factor of the MM resonance, which is defined as the resonance central frequency divided by the spectral width ( ), is very low because of the ohmic loss of metal and the radiative loss of surface mode resonance of MMs.[11–18] Recently, we proposed that GMR can be excited in a planar MM due to its periodic MM grating, and the calculated Q value of the GMR was enhanced greatly by its asymmetric structure compared with that of MM resonance.[19] Not only do the flexible structures of MM make the design of GMRs in MM more diverse, but also the coupling between the GMR and the MM resonance can lead to realizing Fano resonance or electromagnetically induced transparency (EIT). However, such kind of GMR in planar MMs has not been reported experimentally yet. In this paper, GMRs in closed ring resonator (CRR) composed MMs and the coherent interaction between the MM resonance and GMR are numerically and experimentally investigated in the terahertz region. A polarization-insensitive GMR is demonstrated, and the physics mechanism is also interpreted.
), is very low because of the ohmic loss of metal and the radiative loss of surface mode resonance of MMs.[11–18] Recently, we proposed that GMR can be excited in a planar MM due to its periodic MM grating, and the calculated Q value of the GMR was enhanced greatly by its asymmetric structure compared with that of MM resonance.[19] Not only do the flexible structures of MM make the design of GMRs in MM more diverse, but also the coupling between the GMR and the MM resonance can lead to realizing Fano resonance or electromagnetically induced transparency (EIT). However, such kind of GMR in planar MMs has not been reported experimentally yet. In this paper, GMRs in closed ring resonator (CRR) composed MMs and the coherent interaction between the MM resonance and GMR are numerically and experimentally investigated in the terahertz region. A polarization-insensitive GMR is demonstrated, and the physics mechanism is also interpreted.
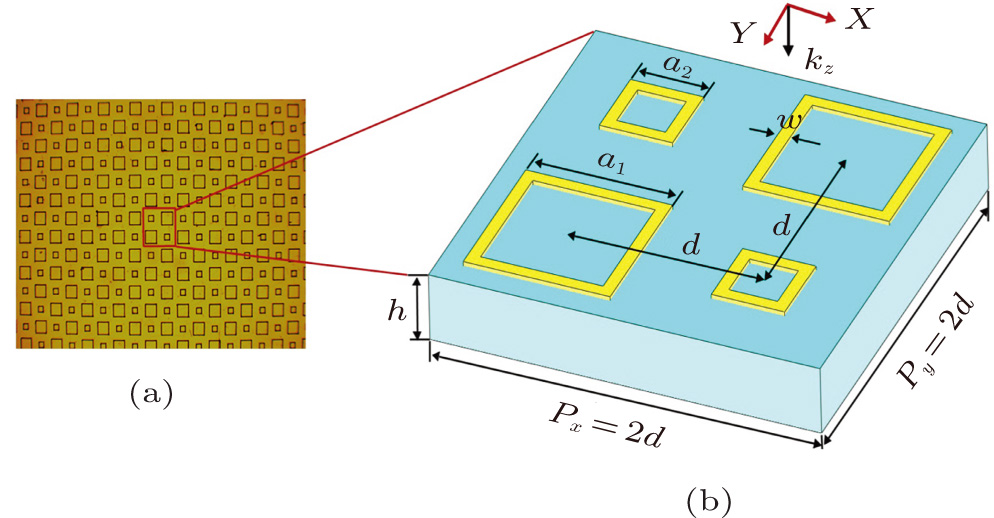
2. Simulations for GMRs in a two-CRR composed MMThe basic unit cell of our proposed hybrid MM on a dielectric substrate (waveguide) consists of two CRRs in different sizes (shown in Fig. 1(a)). The period of the unit cell in the x-direction is  , which is twice of the period in the y-direction. The lengths of the two square rings are a1 and a2, respectively, and their central distance is
, which is twice of the period in the y-direction. The lengths of the two square rings are a1 and a2, respectively, and their central distance is  . Figures 1(b) and 1(c) are the micrographs of two fabricated samples on the polyimide film.
. Figures 1(b) and 1(c) are the micrographs of two fabricated samples on the polyimide film.
The far-field transmission properties of the planar MMs are numerically calculated by using the simulation software CST Microwave Studio in the frequency domain. In simulation, the periodic boundary condition is used in both x and y directions. The lossless waveguide is assumed with a dielectric constant of 3.5 and a thickness of  . Copper is used in fabrication for the metal of MM, and its electrical conductivity is set to be 5.8 × 107 S/m, the metallic stripe
. Copper is used in fabrication for the metal of MM, and its electrical conductivity is set to be 5.8 × 107 S/m, the metallic stripe 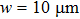 . Figure 2 shows the transmissions of the MMs with different ring lengths when a THz wave with polarization along the x-axis or y-axis is incident normally onto the MMs. Generally speaking, the metallic periodic MM can be partly regarded as a two-dimensional grating, called MM grating,[20] therefore GMRs will be excited by incident electromagnetic wave coupling to the slab dielectric waveguide through diffraction,[1,19] whose frequency is determined by the following grating diffraction equation and the waveguide phase matching condition:
. Figure 2 shows the transmissions of the MMs with different ring lengths when a THz wave with polarization along the x-axis or y-axis is incident normally onto the MMs. Generally speaking, the metallic periodic MM can be partly regarded as a two-dimensional grating, called MM grating,[20] therefore GMRs will be excited by incident electromagnetic wave coupling to the slab dielectric waveguide through diffraction,[1,19] whose frequency is determined by the following grating diffraction equation and the waveguide phase matching condition:
 | |
 | |
where
p is the grating period (
Px along the
x-axis and
Py along the
y-axis),
λ is the wavelength in a vacuum,
n is the refractive index of the substrate,
m is the diffraction order,
θ is the diffraction angle,
h is the thickness of the substrate,
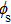
and
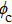
are the additional phases of the total reflections happening at the upper and lower faces of the waveguide, respectively, and
N is the waveguide mode order.
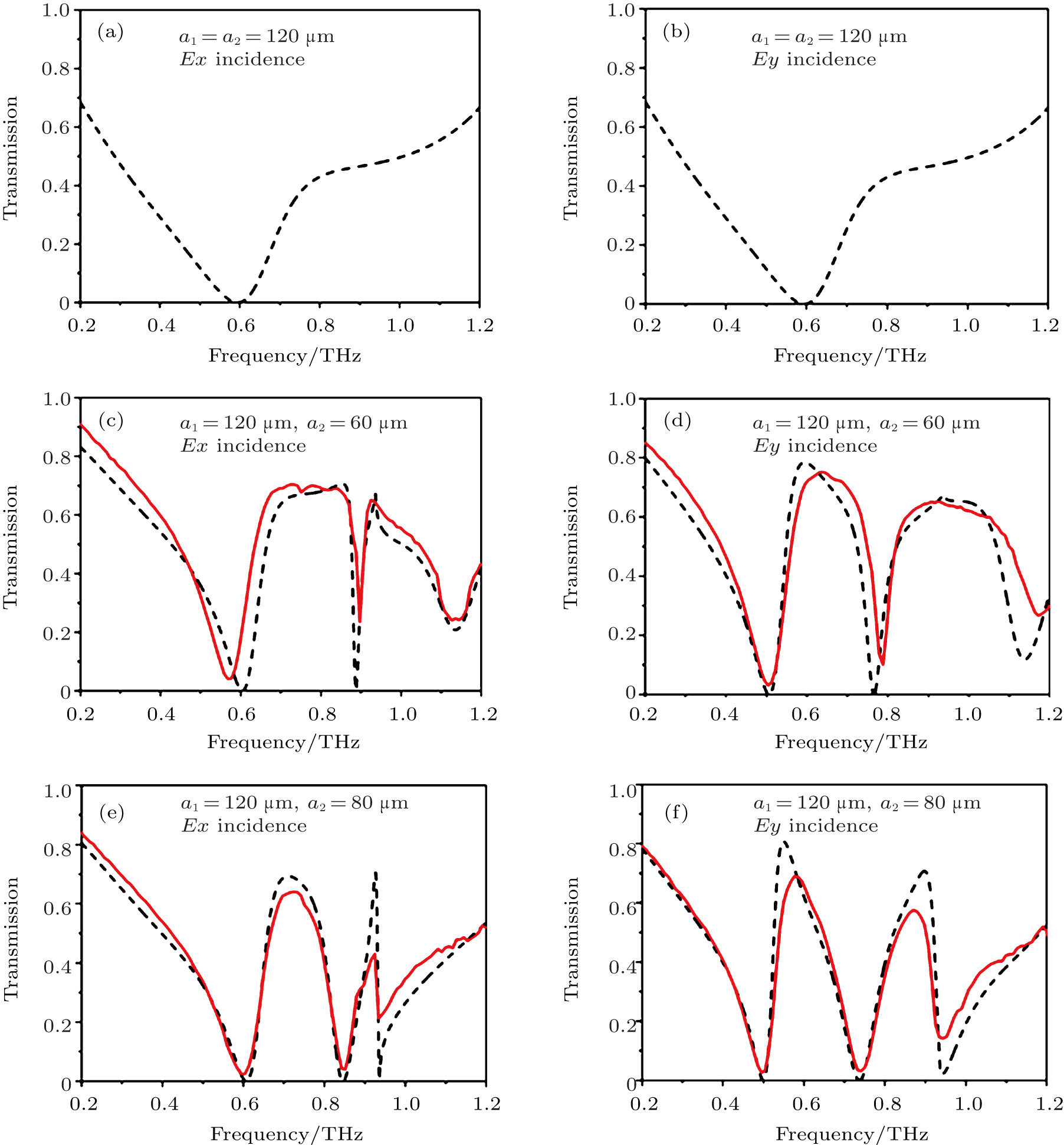
When the lengths of the two rings are equal (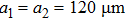 in Fig. 1(a), each ring behaves as a grating bar, thus the periods of the MM grating along the x-direction and y-direction are both d (called d-grating). The calculated frequency of GMR by the first order grating diffraction equation and boundary all reflection condition of the waveguide will fall in the range of 1.0–1.87 THz, which is beyond our interest. It is easy to see from the transmission shown in Figs. 2(a) and 2(b) that only one broad (or low Q) dipolar resonance of the MM exists in the range of 0.2–1.0 THz for both x- and y-polarized incidences, and the central resonant frequency depending on the length of the rings is about 0.6 THz.
in Fig. 1(a), each ring behaves as a grating bar, thus the periods of the MM grating along the x-direction and y-direction are both d (called d-grating). The calculated frequency of GMR by the first order grating diffraction equation and boundary all reflection condition of the waveguide will fall in the range of 1.0–1.87 THz, which is beyond our interest. It is easy to see from the transmission shown in Figs. 2(a) and 2(b) that only one broad (or low Q) dipolar resonance of the MM exists in the range of 0.2–1.0 THz for both x- and y-polarized incidences, and the central resonant frequency depending on the length of the rings is about 0.6 THz.
Once the lengths of the two rings are not equal ( ,
, 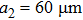 ) in Fig. 1(a), besides the dipolar resonance at ∼0.6 THz, a new dipolar resonance centered at 1.1 THz appears corresponding to the small size ring (shown in Figs. 2(c) and 2(d)). Moreover, the MM grating can be regarded as a compound grating at this circumstance,[10] i.e. in addition to the d-gratings in both x and y directions, a component of 2d-grating (grating with period 2d) in the x direction is formed. Therefore, GMRs will be excited through the first order diffraction by this 2d-grating, whose frequency is in the range of 0.50–0.94 THz. For a thin
) in Fig. 1(a), besides the dipolar resonance at ∼0.6 THz, a new dipolar resonance centered at 1.1 THz appears corresponding to the small size ring (shown in Figs. 2(c) and 2(d)). Moreover, the MM grating can be regarded as a compound grating at this circumstance,[10] i.e. in addition to the d-gratings in both x and y directions, a component of 2d-grating (grating with period 2d) in the x direction is formed. Therefore, GMRs will be excited through the first order diffraction by this 2d-grating, whose frequency is in the range of 0.50–0.94 THz. For a thin  dielectric waveguide, only one GMR of either TM0 or TE0 mode propagating along the x direction can be coupled in terms of Eq. (2), which depends on the polarization of the incident wave.[4] For example, the GMR of the TM0 mode will be coupled under Ex polarized incidence, while the TE0 one appears under Ey polarized incidence. This can be seen from the simulation results shown in the black and dash lines of Figs. 2(c) and 2(d) that there is only one GMR located at 0.89 THz or 0.77 THz, respectively. The distributions of magnetic field
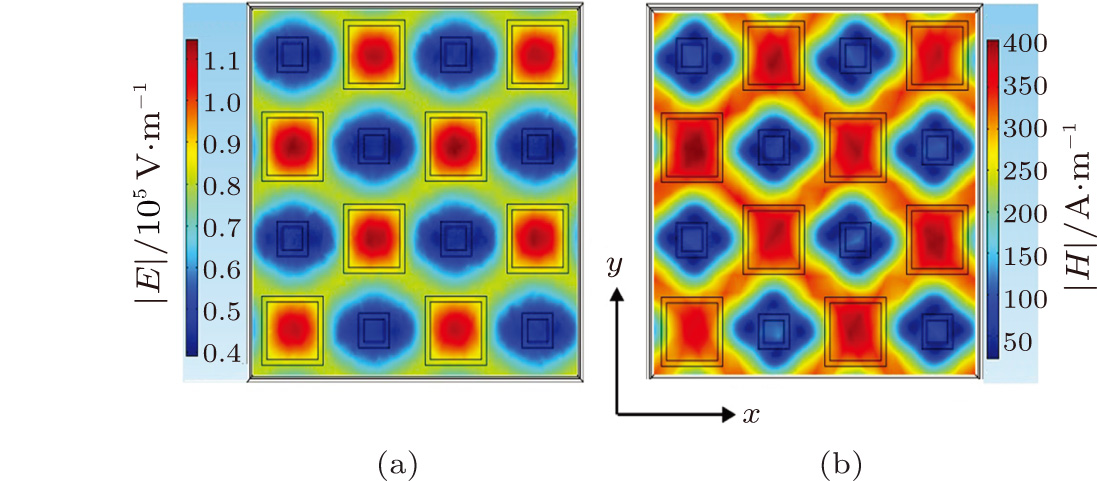
dielectric waveguide, only one GMR of either TM0 or TE0 mode propagating along the x direction can be coupled in terms of Eq. (2), which depends on the polarization of the incident wave.[4] For example, the GMR of the TM0 mode will be coupled under Ex polarized incidence, while the TE0 one appears under Ey polarized incidence. This can be seen from the simulation results shown in the black and dash lines of Figs. 2(c) and 2(d) that there is only one GMR located at 0.89 THz or 0.77 THz, respectively. The distributions of magnetic field  (
( ) and electric field
) and electric field 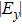 (
( ) in the x–y plane shown in Figs. 3(a) and 3(b) clearly indicate that the GMR at 0.89 THz is TM0 mode, while TE0 mode at 0.77 THz, and the two GMRs are all propagating along the x direction. Moreover, it is easy to find that the Q factor of the TM0 mode is larger than that of the TE0 one. This can be explained by the weak coupling theory,[8,10] in which the grating diffraction efficiency for the TM incidence (Ex polarized incidence in Fig. 1) is smaller than that for TE (Ey polarized incidence),[21] the less diffracted light energy will be coupled to the waveguide, resulting in a high Q value of the GMR.
) in the x–y plane shown in Figs. 3(a) and 3(b) clearly indicate that the GMR at 0.89 THz is TM0 mode, while TE0 mode at 0.77 THz, and the two GMRs are all propagating along the x direction. Moreover, it is easy to find that the Q factor of the TM0 mode is larger than that of the TE0 one. This can be explained by the weak coupling theory,[8,10] in which the grating diffraction efficiency for the TM incidence (Ex polarized incidence in Fig. 1) is smaller than that for TE (Ey polarized incidence),[21] the less diffracted light energy will be coupled to the waveguide, resulting in a high Q value of the GMR.
Because the central frequency of the dipolar resonance can be easily tuned by the ring’s length, whereas the frequency of the GMR is not sensitive to it, we can manipulate the coherent interaction between the dipolar resonance and the GMR simply by changing the ring’s length. The simulated transmissions are shown in black and dash lines in Figs. 2(e) and 2(f), where  and
and  . In this case, the central frequency of one broad dipolar resonance of the MM is shifted down to ∼0.9 THz, and quite close to that of the narrow GMR of TM0, therefore, the strong interaction between the two resonances happens, resulting in a transparency window[22–26] centered at 0.9 THz, as shown in Fig. 2(e). Although the central frequency of the dipolar resonance (∼0.9 THz) is away from the GMR of TE0 (0.77 THz), the weak coupling between them still exists, resulting in broadening of this GMR, as shown in Fig. 2(f).
. In this case, the central frequency of one broad dipolar resonance of the MM is shifted down to ∼0.9 THz, and quite close to that of the narrow GMR of TM0, therefore, the strong interaction between the two resonances happens, resulting in a transparency window[22–26] centered at 0.9 THz, as shown in Fig. 2(e). Although the central frequency of the dipolar resonance (∼0.9 THz) is away from the GMR of TE0 (0.77 THz), the weak coupling between them still exists, resulting in broadening of this GMR, as shown in Fig. 2(f).
As the resonance frequency of the GMR can be easily adjusted by the corresponding grating period or the thickness of the waveguide according to Eq. (2), we will discuss the Q factor of the GMR in the following. The Q factor of the GMR in the conventional waveguide grating is inversely proportional to the grating strength, while its amplitude (from the resonance baseline to the peak in transmission) is just the opposite.[8,10] Like the Fourier component analysis for a compound grating structure,[10] it is easy to deduce that the strength of 2d-grating shown in Fig. 1 is proportional to the size difference of the two rings. Thus, we can define  as the relative depth of 2d-grating modulation, where
as the relative depth of 2d-grating modulation, where  . Figure 4 shows the Q factor and amplitude of TM0 GMR with respect to
. Figure 4 shows the Q factor and amplitude of TM0 GMR with respect to  when a1 is fixed to
when a1 is fixed to  . The size of the two rings chosen larger than
. The size of the two rings chosen larger than 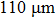 means that the dipolar resonance of the MM is far away from the GMR of the TM0 mode, thus the coupling between them becomes weak. It is easy to see that the smaller the depth of the grating modulation is, the higher Q value of the corresponding GMR we can achieve, but with weaker GMR resonance at the same time. With a low
means that the dipolar resonance of the MM is far away from the GMR of the TM0 mode, thus the coupling between them becomes weak. It is easy to see that the smaller the depth of the grating modulation is, the higher Q value of the corresponding GMR we can achieve, but with weaker GMR resonance at the same time. With a low  (
( ), the Q factor of TM0 GMR can reach upto 1000. Here, we should mention that the high Q factor of the GMR will be affected by the loss of the substrate. If we consider the loss tangent of the polyimide (PI) film as 0.05,[27] the Q factor of the GMR will dramatically decrease to below 200. In order to realize high Q of the GMR experimentally, a thinner and/or smaller lossy material should be adopted. For example, the benzocyclobutene (BCB) film can be used as the substrate because of its low loss tangent of ∼0.009 at 1 THz.[28] The Q factor and amplitude of TM0 GMR for
), the Q factor of TM0 GMR can reach upto 1000. Here, we should mention that the high Q factor of the GMR will be affected by the loss of the substrate. If we consider the loss tangent of the polyimide (PI) film as 0.05,[27] the Q factor of the GMR will dramatically decrease to below 200. In order to realize high Q of the GMR experimentally, a thinner and/or smaller lossy material should be adopted. For example, the benzocyclobutene (BCB) film can be used as the substrate because of its low loss tangent of ∼0.009 at 1 THz.[28] The Q factor and amplitude of TM0 GMR for  -thickness BCB film are also shown in Fig. 4. A thinner BCB film can be used to further enhance the Q factor of GMR.
-thickness BCB film are also shown in Fig. 4. A thinner BCB film can be used to further enhance the Q factor of GMR.
3. Polarization-insensitive GMRs in a four-CRR composed hybrid MMThe four-CRR composed hybrid MM we proposed is shown in Fig. 5. Obviously, the transmission of the MM under Ex incidence is the same as that under Ey incidence due to its symmetric structure. We set the parameters of  ,
,  ,
,  , and other parameters are the same as those used in Fig. 2. The simulated transmission under Ex polarization incidence is shown in Fig. 6 (dark and dash line). It is clear to see that there is a GMR located at ∼0.9 THz. Here we should emphasize that this GMR is totally different from that of TM0 shown in Fig. 2(c), i.e., this GMR is not coupled by the 2d-grating either in the x- or y-direction. In fact, it is coupled by 45° tilting gratings, which can be proved as follows. From Fig. 5, it can be seen that there exist two grating components tilting 45° and −45° to the x-axis, whose periods are both
, and other parameters are the same as those used in Fig. 2. The simulated transmission under Ex polarization incidence is shown in Fig. 6 (dark and dash line). It is clear to see that there is a GMR located at ∼0.9 THz. Here we should emphasize that this GMR is totally different from that of TM0 shown in Fig. 2(c), i.e., this GMR is not coupled by the 2d-grating either in the x- or y-direction. In fact, it is coupled by 45° tilting gratings, which can be proved as follows. From Fig. 5, it can be seen that there exist two grating components tilting 45° and −45° to the x-axis, whose periods are both  , and in terms of the grating diffraction equation, the resonance frequency of the corresponding GMRs will lie in the range of 0.71–1.33 THz (here the tilting grating components of period
, and in terms of the grating diffraction equation, the resonance frequency of the corresponding GMRs will lie in the range of 0.71–1.33 THz (here the tilting grating components of period 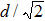 are not considered for the same reason as the d-gratings in Section 2). According to the phase matching condition of Eq. (2), if the thickness of the waveguide increases by
are not considered for the same reason as the d-gratings in Section 2). According to the phase matching condition of Eq. (2), if the thickness of the waveguide increases by  , where λ is the wavelength of GMR of either TM0 or TE0 mode for waveguide thickness h, and θ can be calculated by Eq. (1) for the corresponding GMR, then the GMR of TM1 or TE1 will appear at the same wavelength λ. This is confirmed by our simulations for the tilting grating with period
, where λ is the wavelength of GMR of either TM0 or TE0 mode for waveguide thickness h, and θ can be calculated by Eq. (1) for the corresponding GMR, then the GMR of TM1 or TE1 will appear at the same wavelength λ. This is confirmed by our simulations for the tilting grating with period  , but invalid for the 2d-gratings. Furthermore, we can obtain the electric field distribution in the x–y plane of the GMR at 0.9 THz as shown in Fig. 7(a), which clearly reveals that there are indeed two GMRs of the TE0 mode with the same resonance frequency, propagating along 45° and −45° to the x-axis, respectively. Thus, we can conclude from Fig. 6 that there is no GMR induced by 2d-gratings both in x and y directions for this four-CRR structure.
, but invalid for the 2d-gratings. Furthermore, we can obtain the electric field distribution in the x–y plane of the GMR at 0.9 THz as shown in Fig. 7(a), which clearly reveals that there are indeed two GMRs of the TE0 mode with the same resonance frequency, propagating along 45° and −45° to the x-axis, respectively. Thus, we can conclude from Fig. 6 that there is no GMR induced by 2d-gratings both in x and y directions for this four-CRR structure.
Consider the two facts: (i) there exist two tilting gratings with the same pattern and perpendicular to each other, (ii) the GMR of the TE mode is coupled by the electric field of the incident wave perpendicular to the grating, whereas the TM one is coupled by the electric field of the incidence parallel to the grating. Thus, two GMRs of the TM0 mode should be coupled by the same tilting gratings under Ex incidence, just as that for GMRs of TE0. This can be seen from Fig. 6 that there is a transparent window at 1.2 THz, which is attributed to the interaction between the dipolar resonance of the MM (seen in Figs. 2(c) and 2(d)) and the two GMRs of TM0. The magnetic field distribution at 1.2 THz in the x–y plane shown in Fig. 7(b) reveals the GMRs of the TM mode in nature. Furthermore, numeric and experimental results also demonstrate that the transmission of the MM shown in Fig. 5 including GMRs coupled by the tilting gratings is insensitive to the polarization of the incident wave.
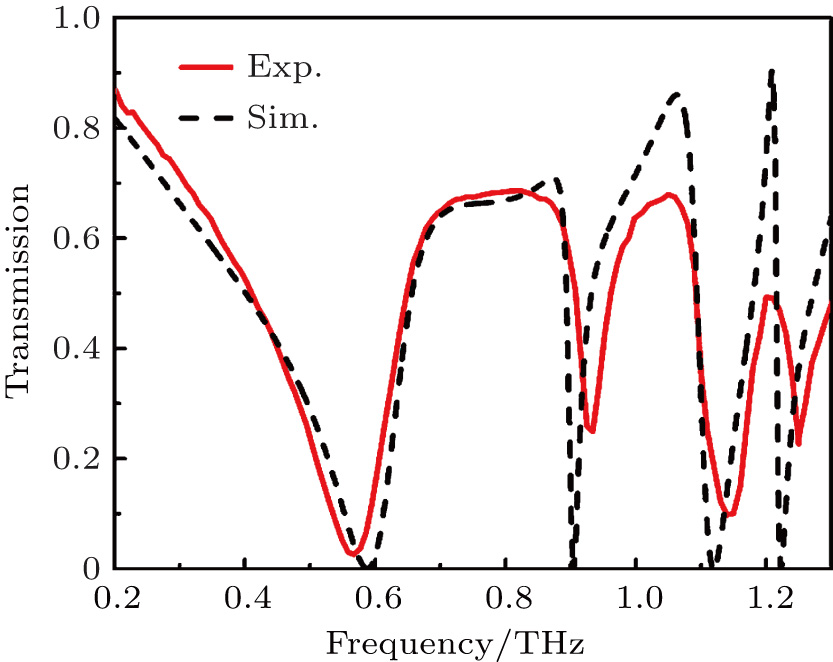
4. Fabrication of MMs and measured resultsThe planar MMs were fabricated based on laser-induced site-selective silver seeding on polyimide (PI) film for electroless copper plating in our laboratory,[29,30] in which Ag nanoparticles were generated from PVP/AgNO3 colloid coated on polyimide film by laser direct writing using a blue laser diode, then the Ag nanoparticles were used as seeds to induce selective electroless plating on the polyimide film and form patterned copper deposition. The micrographs of two experimental samples are shown in Figs. 1(b) and 1(c), and the geometric parameters are the same as those used in the simulation in Figs. 2(c) and 2(e). The sizes of the fabricated samples are 30 mm × 30 mm. The far-field transmission spectra were measured by THz time domain spectroscopy (THz-TDS) under x- and y-polarized incidences. In our measurement, the THz beam radiated from the photoconductive antenna was firstly collimated by an off-axis parabolic mirror with 1-inch diameter, then incident normally on the samples, the transmitted beam was detected by electro-optic sampling. The tramsmission spectra are shown in a red line in Figs. 2(c)–2(f). It is easy to see that the measured resonance frequencies are in good agreement with the simulations, except that there is a small shift for the dipolar resonance at ∼0.6 THz in Fig. 2(c). This is caused by the fabrication accuracy for the width of the metallic stripe in the electroless copper plating process, while the accuracy for the length of CRR or period of MM depending on the translation stage is much higher. But there are some differences in the transmission amplitude between the simulated resonance peaks and the experimental results, especially in the transmission of the GMR, which we attribute to the loss of the substrate. The impact of the waveguide loss on the surface resonances of MM can be neglected because of the thin waveguides, but it will greatly influence the GMRs, especially those with high Q shown in Figs. 2(c) and 2(e) and Fig. 6. Moreover, the measured resonance will be distorted by the limited spectral resolution of the measurement system (∼10 GHz) for a GMR with higher Q. The measured results shown in Fig. 6 are also in good agreement with the simulations for the fabricated four-CRR composed hybrid MM, and the polarization-insensitive property of the transmission is also demonstrated through rotating the MM sample.
5. ConclusionWe have theoretically and experimentally demonstrated guided mode resonances in a two-ring-resonator consisted planar metamaterial at the THz regime. Both the spectral property of GMR, and the coherent coupling between the GMR and the dipolar resonance of MM resulting in the realization of Fano resonance or an EIT-like response can be easily controlled by adjusting the length of the two ring resonators. Furthermore, polarization-insensitive GMRs in a four-ring-resonator consisted of MM were demonstrated, where the GMRs of both TE and TM modes are attributed to the diffraction coupling by the two ±45° tilting gratings. These results are useful for their applications in ultra-sensitive label free sensing, filtering, or slow light based devices both in THz and optical ranges.