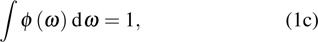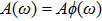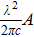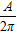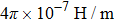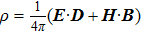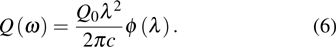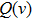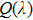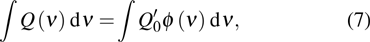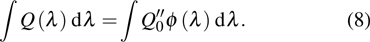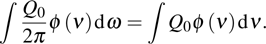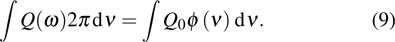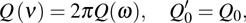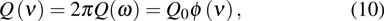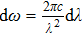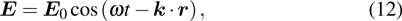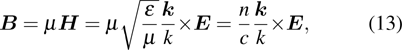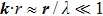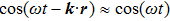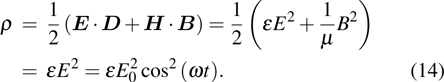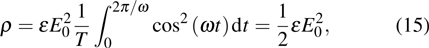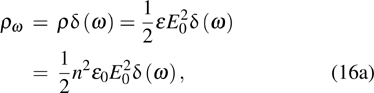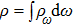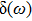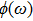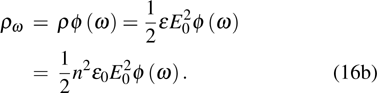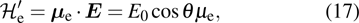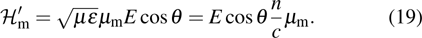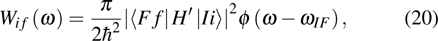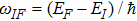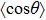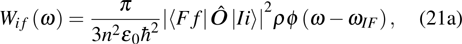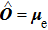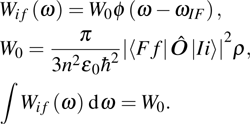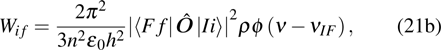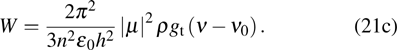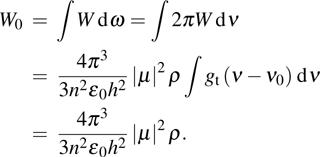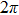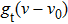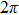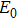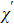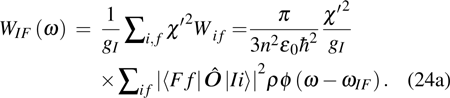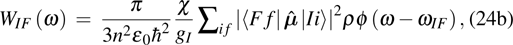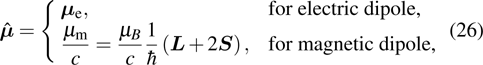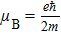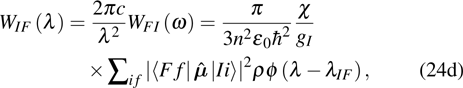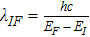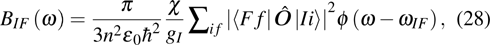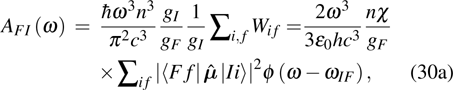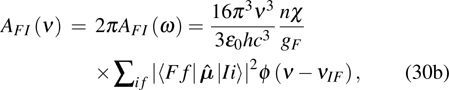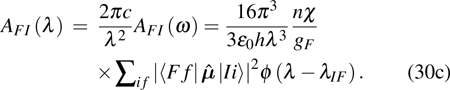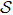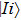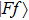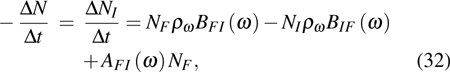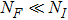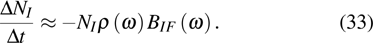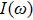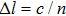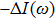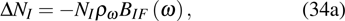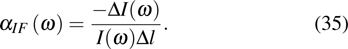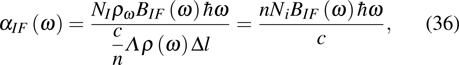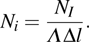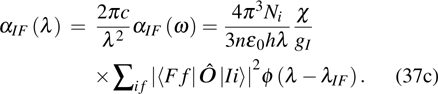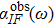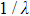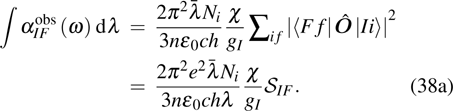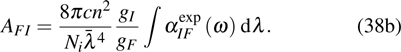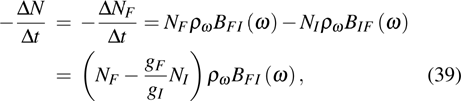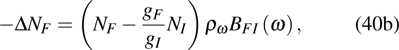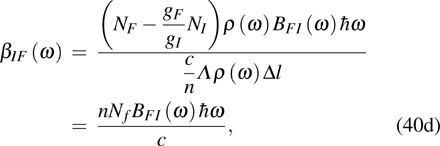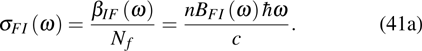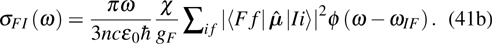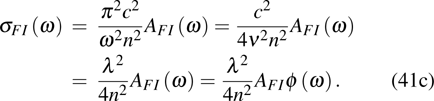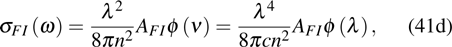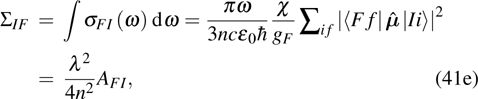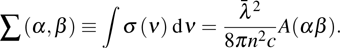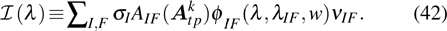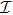Cite this Article
Zhang Qing-li, Sun Guihua, Gao Jin-yun, Sun Dun-lu, Luo Jian-qiao, Liu Wen-peng, Zhang De-ming, Shi Chaoshu, Yin Shaotang. Profile function properties & optical transition formulae. Chinese Physics B, 2017, 26(7): 077803  
Permissions
Profile function properties & optical transition formulae
Zhang Qing-li1, †, Sun Guihua1, Gao Jin-yun1, Sun Dun-lu1, Luo Jian-qiao1, Liu Wen-peng1, Zhang De-ming2, Shi Chaoshu1, Yin Shaotang1
The Key Laboratory of Photonic Devices and Materials, Anhui Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Hefei 230031, China
Physics Department, the University of Science and Technology of China, Hefei 230026, China

 

† Corresponding author. E-mail: zql@aiofm.ac.cn

Abstract

Profile function properties with different variables are discussed, the formulae of stimulated absorption, spontaneous and stimulated emission, absorption and emission coefficients, and cross sections are deduced, and some confusing issues are clarified.

PACS: 78.55.-m;78.60.Lc;75.10.Dg
Keyword:optical transition;profile function
1. Introduction

Due to defects, strain, disorder, lattice vibration, and so on in solids, an ideal optical absorption or emission transition line of rare earth ions, described by the Dirac function δ, is usually a wider band, which can be described by a profile function ϕ, such as the Voigt function,[1–4] with independent variable wavelength λ, frequency ν, or angle frequency ω, which has the following relationships:

where c is the light speed in vacuum. The frequency ν or angle frequency ω of a light source is fixed when it transmits in a medium or vacuum, so equations (2a)–(2c) are suitable for the medium or vacuum, and λ is the wavelength in vacuum. The δ function has the same relationships as in Eqs. (2a)–(2c). Based on this, a physical quantity such as spontaneous transition rate can be written as

From Eq. (3), it seems that the transition rate has very different amplitudes if a profile function has a different independent variable, e.g., , , or A in Eq. (3), which easily causes much confusion in application.

On the other hand, there are many unit systems of electromagnetics, such as the rationalized MKSA system of units, the absolute electrostatic system of units (e.s.u. or CGSE), the absolute electromagnetic system of units (e.m.u. or CGSM), and the Gauss system of units (CGS). Electromagnetic quantities and formulae usually have a variety of values and expressions. For example, the dielectric constant ε0 and permeability μ0 in vacuum are 8.85× 10−12 F/m and in MKSA, but both are 1 in CGS; electromagnetic energy density in MKSA, but in the Gauss system of units. Although international system of units has been widely used recently, many very different systems of units have been used in references, which were usually not declared explicitly, resulting in confusion about published calculations. It is necessary to clarify transition formula expressions in order to perform spectral analysis or calculation.

The present work first discusses the distribution property of a physical quantity with a profile in wavelength, frequency, or angle frequency, and further clarifies the formulae of emission and absorption. The unit system of this work is SI units.

2. General properties of profile functions

Assume a physical quantity Q, such as the absorption coefficient, emission or absorption cross section, or transition probability, with the variable angle frequency ω and profile is expressed as

Substituting Eqs. (2b) and (2c) into Eq. (4), we obtain the following equations:

Although equations (5) and (6) are expressed in profile or , either should be integrated against variable ω. In order to obtain the distribution of Q with variable ν or λ, and should satisfy the relationships

Then, integrating Eq. (5) versus ω, the left is changed as

and the right is changed as

The left integral should be equal to the right integral, so

Comparing Eq. (9) with Eq. (7), we obtain the following equation:

and then
which should be integrated against ν on both sides directly to obtain the total quantity Q0.

Integrate Eq. (10) versus ω, using , through the same procedure, we obtain and , and then

which should be integrated against λ directly on both sides to obtain the total quantity Q0.

In summary, if a physical quantity Q can be expressed as the product of amplitude and a profile function with variable wavelength, frequency, or angle frequency, it has the same distribution expression and amplitude Q0 in different variable spaces, and the profile function value is normalized in the respective variable spaces. This reflects the fact that a physical quantity should be the same no matter how it is described by a profile function in variables of wavelength, frequency, or angle frequency.

3. Transition formulae in absorption and emission spectra
3.1. Optical absorption and emission

Let us consider a plane electromagnetic wave, its electric and magnetic vector can be written as

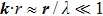
where μ is the permeability, ε is the dielectric constant, n is the refractive index, c is the light speed in vacuum, and is the wave vector. In the atomic size region, , , the electric field can be seen as a uniform field whose energy density for a linear medium[5] is

During a period , the average energy density

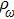
and then the average energy density per unit angle frequency can be written as
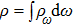
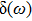
and should have dimension Hz−1, which satisfies the relationship . If the energy is distributed in a finite region near ω, then should be replaced by :

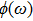
The additional energies 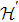induced by electric and magnetic dipole and 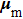in the time-dependent electromagnetic field are

With Eq. (13), equation (18) is written as

Consider a transition from the initial state 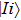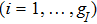with lower energy EI to ( with higher energy EF. Where i and f are used to disignate degenerated states, the transition probability caused by the electric or magnetic dipole should be written with respect to angle frequency ω according to Eq. (2.4.7) in Ref. [6]:

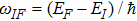
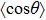
where the δ function in the reference has been replaced with a profile function ϕ, , , h is Planck’s constant, ε0 is the dielectric constant in vacuum. For randomly oriented dipoles, mean value over all dipole orientations is 1/3, so substituting Eq. (16), (17), or (19) into Eq. (20) gives
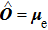
with for the electric dipole and for the magnetic dipole. Equation (21a) implies the following equations:

For convenient comparison, we can substitute Eq. (2c) into Eq. (21a), yielding

which corresponds to Eq. (2.4.30) in Ref. [6]

It can be seen that the right side of either Eq. (21a) or (21b) is equal to that of Eq. (21c), but all of them should be integrated versus ω in order to obtain the total transition probability

If we want to know the total value W0 of W by integrating (21c) versus ν directly on both sides, W should be written as

In fact, this has been proved in Section 2; the factor 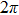is from the condition that equation (21c) should be integrated against ω, even though it contains the profile function 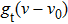. Furthermore, there exists a difference of a factor of 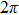in the absorption probability formulae (24a)–(24d), (28), and emission probability formulae (30a)–(30c) in the following contexts.

Consider that the local electric field correction 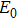for the electric dipole transition should be multiplied by a correct factor in Eqs. (21a)–(21c). According to Eqs. (17) and (19) in Ref. [7], for an electron in a cubic insulator lattice site with relative permittivity , 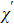should be

Then the average transition rate WIF of is

Furthermore, n is separated from to form a medium correction coefficient for the magnetic dipole transition, and equation (24a) is written as

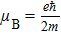
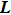
where is the Bohr magneton, e and m are the charge and mass of an electron, ℏ is Planck’s constant divided by 2π, and and are the orbital and spin momentum operators. According to the conclusion in Section 2, WIF can be written in terms of frequency or wavelength immediately as
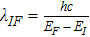
where . Consider the relationship
and the Einstein relation
where BIF is Einstein’s stimulated absorption coefficient, AFI is Einstein’s spontaneous emission coefficient, BFI is Einstein’s stimulated emission coefficient. Then the spontaneous emission transition probability AIF can be written as

It is usually to call 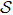line strength with dimension 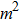, whose value is

3.2. Absorption coefficient and emission cross section
3.2.1. Absorption coefficient

The ion number variation rate in EI caused by the stimulated absorption, stimulated and spontaneous emission between 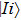and 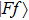is given by

where NI is the absorption ion center number in the volume passed by light beam per unit time. For a general absorption measurement, ,

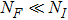
Assume a light beam with cross section Λ and intensity 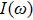, which is the energy passing through Λ per unit time, passes through a medium by 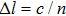and decreases by 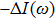per unit time, then

The absorption coefficient is defined as

Substituting Eqs. (34a)–(34c) into Eq. (35) gives

where Ni is the absorption ion concentration,

Substituting Eq. (28) into Eq. (36) leads to

According to the conclusion in Section 2, the following equation can be written immediately:

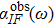
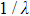
can be measured experimentally and is labeled as here; then integrate (37c) against λ directly, take as a constant and for a sharp absorption band; then

Based on Einstein’s relationship and Eq. (38a), AFI can be obtained from the absorption spectrum integral as

3.2.2. Emission cross section

For laser operation, spontaneous radiation does not need to be considered, so equation (32) is changed to

Like the absorption coefficient, the emission coefficient or gain coefficient β is defined as

Substitute Eqs. (34b), (40b), (40c) into Eq. (40a),

where
which is the inversion activator number per unit volume. The emission cross section is defined as

Substituting Eq. (28) into Eq. (41) gives

Using Einstein’s relationship Eq. (29), can be written as

Substituting Eqs. (2b) and (2c) into Eq. (41c), we obtain

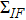
which is the F–L formula. Note that λ in Eq. (41a)–(41d) is the wavelength in vacuum, and if we want to know the emission cross section integral value , all of them should be integrated against ω, giving
which is the amplitude of the emission cross section and can be multiplied by a profile function to give its distribution in frequency, wavelength, or angle frequency space. Comparing (41e) with Eq. (2) in Ref. [8], we find that the integrated emission cross section is unreasonable:

3.3. Related aspects of full profile fitting of the emission spectrum

If the emission spectrum of a rare earth ion is fitted by the full profile method, is described by[9]

According to the conclusion in Section 2, should have the same value and is independent of the variable type of , so the intensity should have the same expression and the same should be obtained regardless of whether the emission spectrum is described with wavelength, frequency or angle frequency.

4. Conclusion

A physical quantity Q such as absorption and emission that can be expressed as a product of amplitude and a profile function with variable wavelength, frequency, or angle frequency has the same distribution expression and amplitude Q0 in any of these variable spaces, and the profile function value is normalized in the respective space. Optical transition formulae about emission and absorption were deduced, and the related confusions were clarified.

Reference
[1] Yin Z Q Wu C Gong W Y Gong Z K Wan Y J 2013 Acta Phys. Sin. 62 233301 in Chinese
[2] Y Z Q Wu C Wan Y J Li X C 2012 Spectroscopy and Spectral Analysis 32 1189
[3] Wu C 2013 Master Dissertation Baoding North China Electric Power University in Chinese
[4] Gao Z 2000 Laser J. 21 36
[5] Guo S H 2004 Electrodynamics 3 Beijing Higher Education Press 142 143
[6] Svelto O Hanna D C 1998 Principles of Lasers 5 New York Plenum Press 34 40
[7] Kittel C 2005 Introduction to Solid State Physics 8 Hoboken John Wiley & Sons Inc 462 463
[8] Caird J A Deshazer L G Nella J 1975 IEEE J. Quantum Electron. QE-11 874
[9] Zhang Q L Sun G H Ning K J Shi C S Liu W P Sun D L Yin S T 2016 Chin. Phys. 25 117802