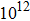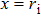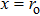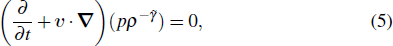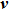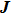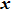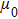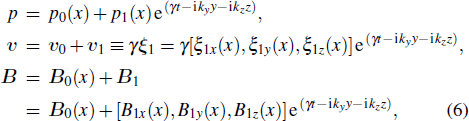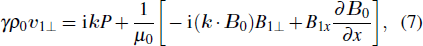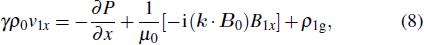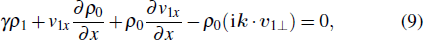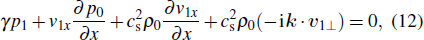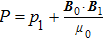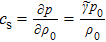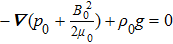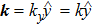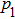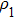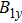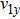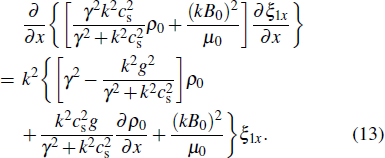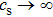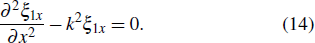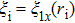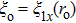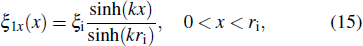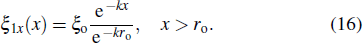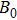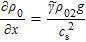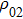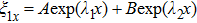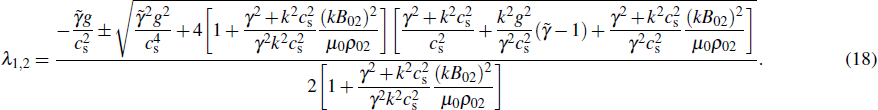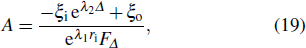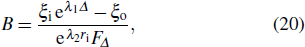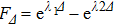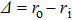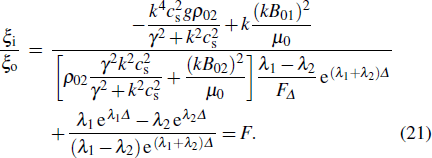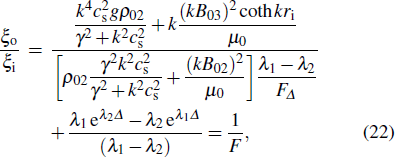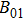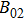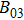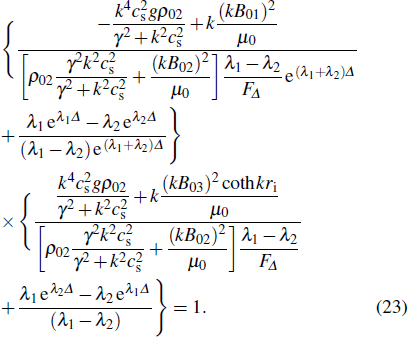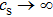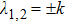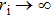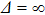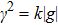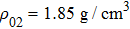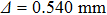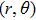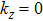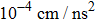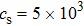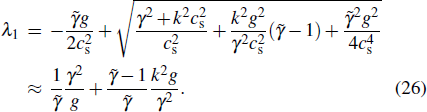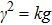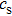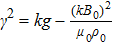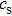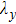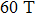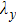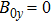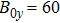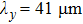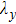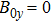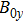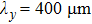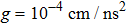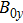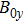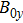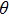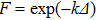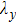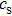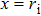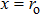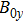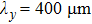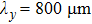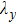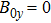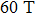1. IntroductionIn the magnetized liner inertial fusion (MagLIF), which is proposed by the Sandia National Laboratories, the preheated and premagnetized fuel is compressed and confined by a cylindrical Z-pinch liner.[1] In recent integrated MagLIF experiments on the Z machine, over 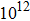 fusion neutrons were generated, which shows great potential of MagLIF in driving inertial confinement fusion.[2] The most important physical problem in MagLIF is the magneto-Rayleigh–Taylor (MRT) instability, which is inherent to Z-pinch implosions.[2–8] The development of MRT instability may cause the disruption of liner implosions and the severe mixing of fuel with the liner, and then limit the fuel to reach ignition condition.[1]
fusion neutrons were generated, which shows great potential of MagLIF in driving inertial confinement fusion.[2] The most important physical problem in MagLIF is the magneto-Rayleigh–Taylor (MRT) instability, which is inherent to Z-pinch implosions.[2–8] The development of MRT instability may cause the disruption of liner implosions and the severe mixing of fuel with the liner, and then limit the fuel to reach ignition condition.[1]
MRT instability in magnetohydrodynamics (MHD) was firstly studied by Chandrasekhar in 1961.[9] Harris studied the MRT instability of an infinitesimal thickness cylindrical shell in a magnetic field.[10] The gradient effects for a particular exponential profile in density and magnetic field were also studied.[11] Zhang et al. discussed the effect of equilibrium shear flow on enhancing MRT instability because of its coupling with a Kelvin–Helmholtz-type instability.[12] Bud'ko et al. studied the stability of dynamic Z pinches and theta pinches and found that in the case of a dynamic Z-pinch, the growth rate is much higher than that in the equilibrium case in 1989.[13] Bellan obtained the dispersion relation and analyzed the MRT instability in an incompressible magnetized plasma.[14] These studies were performed by using two-region model with vacuum and infinite plasmas. For MagLIF, Lau et al. firstly developed a three-region model, which consists of vacuum, liner and fuel, to analytically study the characteristics of MRT instability in a finite slab using the ideal MHD model.[15] Later, authors also studied the effect of magnetic shear on the MRT instability and the feedthrough of outer surface ripples originated from MRT instability on inner surface perturbations.[16,17] Recently, authors studied the MRT instability in cylindrical shells analytically and designed special magnetic field to mitigate MRT instability.[18–20] Above theoretical studies are mainly based on incompressible assumption. However, it is known that the temperature of liner plasmas is relatively low during the liner implosion, because the liner is very heavy in the MagLIF concept compared to the large radius wire-array Z-pinch. In this case, the compressibility may play an important role on MRT instability, deserving careful investigation.
In this paper, the MRT instability in compressible three-region plasmas is theoretically investigated. The dispersion relation of MRT instability is derived using a slab model in Section 2, and the characteristics of MRT instability in (x, y) plane is discussed in Section 3 . The summary is given in Section 4.
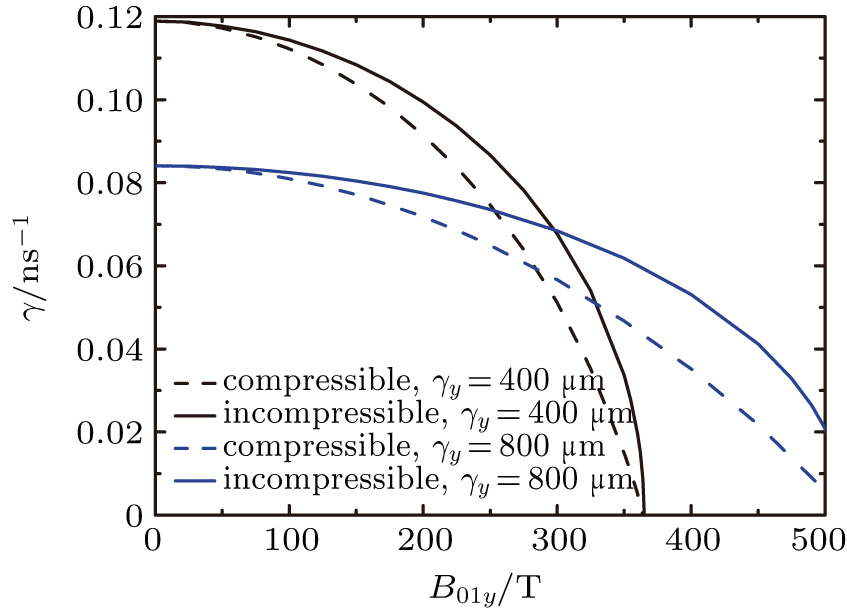
2. Derivation of dispersion relationIn this paper, we use a three-region slab model to analyze MRT instability in MagLIF as shown in Fig. 1. Region I represents the vacuum, region II represents the metal liner, and region III represents the fuel. x = 0 is the axis of the liner, and 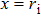 ,
, 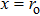 are the position of the inner and outer surfaces of the liner, respectively.
are the position of the inner and outer surfaces of the liner, respectively.
In the rest frame of the outer interface, the ideal MHD equations can be written as follows:
where
ρ and
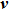
are the mass density and the velocity, respectively;
p and
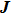
are the plasma pressure and the current density;

is the magnetic field,
g is the equivalent gravity in the
x direction;
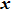
is the unit vector, and
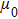
is the free space permeability.

is the adiabatic coefficient. The pressure, velocity, and magnetic field can be written in the perturbation form
where quantities with a subscript 0 and quantities with a subscript 1 are the equilibrium quantities and the small signal quantities, respectively. By linearizing Eqs. (
1)–(
5) and

, the perturbation quantities can be given by
where
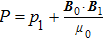
·

is the wave vector.
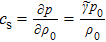
is the acoustic velocity. The equilibrium condition is written as
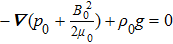
. In this paper, we only study the MRT instability in (
x,
y) plane as shown in Fig.
1, so we set
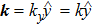
,

, and

. By eliminating
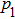
,
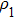
,
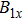
,
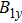
,
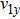
using Eqs. (
7)–(
12), we can obtain an eigenvalue equation of perturbation displacement as follows:
Considering that the plasmas of region I and region III are incompressible (
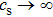
), the density

and the magnetic field

are constant and uniform, then equation (
13) can be written as
Designating
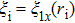
and
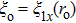
, the solution to Eq. (
14) is given by
Considering that the plasma of region II is compressible and the magnetic field
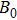
is constant and uniform, and
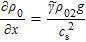
, equation (
13) can be written as
where
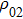
is the density of the liner. The solution of the
above equation is
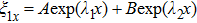
, where
Because the perturbation displacement is continuous at the interface, the values of
A and
B can be obtained from Eqs. (
15)–(
18) as follows:
where
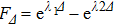
and
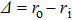
is the liner thickness. Then we integrate Eq. (
13) across the outer surface to yield
Similarly, using the above method at the inner surface, we can obtain
where
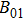
,
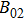
, and
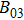
are the magnetic field of region I, region II, and region III, respectively.
F is the feedthrough factor, which is defined as the ratio of the perturbation displacement at the two interface, can be used to describe the feedthrough effect between the perturbations of the two liner surfaces. Employing Eqs. (
21) and (
22), we can obtain a dispersion relation of the growth rate

of MRT instability as
The analytic solution of Eq. (23) is hardly obtained, and the growth rate can be numerically calculated. However, we can simplify Eq. (23) and get the analytic growth rate in several limiting situations. Firstly, in the incompressible condition 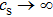 ,
, 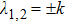 , equation (23) is then reduced to
, equation (23) is then reduced to
which is consistent to that in Ref. [
21]. Setting
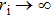
,
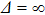
, and
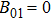
, equation (
24) will be reduced to

, which is the classical form in two-region model. In the case of zero magnetic field, it is further reduced to
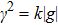
.
Secondly, in the case of zero magnetic field and large liner thickness, equation (23) will also be reduced to the dispersion relation as that in Ref. [22], which will be discussed in the following section.
3. MRT instability in (x, y) planeIn this paper, we choose the typical liner quantities on the Z experiments as examples to analyze the MRT instability.[2,23,24] The liner material is beryllium and its density is 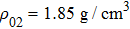 . The liner thickness is
. The liner thickness is 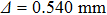 .
.
For MRT instability developing in (x, y) plane, which corresponds to 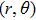 plane in cylindrical liner implosions, we can set
plane in cylindrical liner implosions, we can set 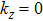 . In this case, only azimuthal magnetic field
. In this case, only azimuthal magnetic field  will affect the development of MRT instability. In MagLIF, typical implosion distance is several millimeters and the implosion time is several tens of nanoseconds, causing a high acceleration to
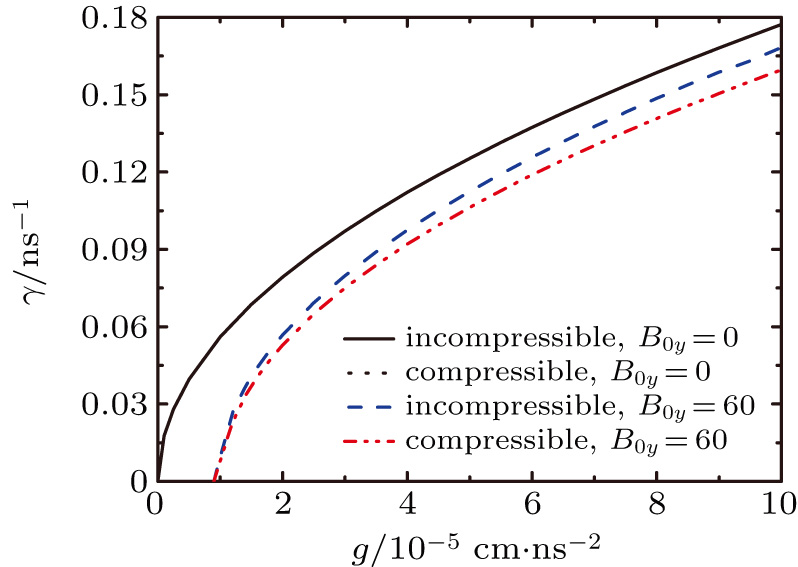
will affect the development of MRT instability. In MagLIF, typical implosion distance is several millimeters and the implosion time is several tens of nanoseconds, causing a high acceleration to 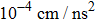 . Figure 2 describes the variations of the growth rate
. Figure 2 describes the variations of the growth rate  with the gravity g in compressible and incompressible situations for different magnetic field in the case of
with the gravity g in compressible and incompressible situations for different magnetic field in the case of 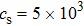 . It is shown that the growth rate in compressible assumption is approximately the same as that in incompressible assumption when the magnetic field is zero. However, in the presence of magnetic field the growth rate is obviously decreased in compressible condition compared to that in incompressible condition.
. It is shown that the growth rate in compressible assumption is approximately the same as that in incompressible assumption when the magnetic field is zero. However, in the presence of magnetic field the growth rate is obviously decreased in compressible condition compared to that in incompressible condition.
In order to explain this phenomenon, we firstly discuss the situation of zero magnetic field and large liner thickness 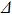 . In this case, the growth rate can be simplified as
. In this case, the growth rate can be simplified as
If the acoustic velocity

is very large,

is
reduced to
k, thus giving the growth rate

. If

,
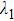
can be given by
Equations (
25) and (
26) will also yield the same growth rate
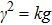
as that in very large
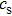
. That is to say, compressibility will not obviously change the MRT development in the case of zero magnetic field. However, when the magnetic field is present and is frozen in the plasma, it will also be compressed as the plasma is compressed. Hence, it can provide stronger restoring force to mitigate MRT instability when the plasma is compressible. In order to further investigate the compressibility effect on MRT instability, the variations of the growth rate

with the acoustic velocity
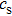
are plotted in Fig.
3. It is obviously shown that the growth rate is nearly independent of
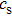
in the case of zero magnetic field. The growth rate increases with
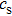
when the magnetic field is 60 T or 100 T. When

is very large, the growth rate will approach the classical
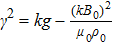
, as shown in Fig.
3.
It is noted that the growth rate is remarkably dependent on the perturbation wavelength. Figure 4 shows the variations of growth rate  with the perturbation wavelength
with the perturbation wavelength 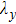 with magnetic field
with magnetic field  and
and 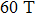 . It is shown that the growth rate decreases monotonically with
. It is shown that the growth rate decreases monotonically with 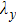 when
when 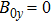 T. However, the growth rate reaches a maximal value when
T. However, the growth rate reaches a maximal value when 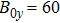 T at
T at 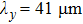 . Furthermore, the presence of magnetic field has a stronger effect on mitigating smaller wavelength perturbations.
. Furthermore, the presence of magnetic field has a stronger effect on mitigating smaller wavelength perturbations.
Clearly, large wavelength perturbations are more serious for MRT instability. The variations of growth rate with 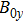 in the case of
in the case of 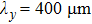 and
and  are compared in compressible and incompressible condition in Fig. 5 for
are compared in compressible and incompressible condition in Fig. 5 for 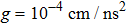 . It is shown that as the magnetic field increases, the growth rate is remarkably decreased and even be reduced to zero whether in compressible condition or in incompressible condition. It is also shown that the longer the perturbation wavelength is, the higher the
. It is shown that as the magnetic field increases, the growth rate is remarkably decreased and even be reduced to zero whether in compressible condition or in incompressible condition. It is also shown that the longer the perturbation wavelength is, the higher the 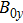 is needed to decrease the growth rate to zero. For the case of large perturbation wavelength 400
is needed to decrease the growth rate to zero. For the case of large perturbation wavelength 400  , when
, when 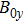 exceeds 364 T, the growth rate is decreased to zero. For the smaller wavelength perturbation, it is more easy to decrease the growth rate to zero. As is known that during the liner implosion,
exceeds 364 T, the growth rate is decreased to zero. For the smaller wavelength perturbation, it is more easy to decrease the growth rate to zero. As is known that during the liner implosion, 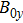 will increase to over 1000 T. In this case, the growth rate of MRT instability for almost all perturbation wavelengths can be decreased to zero. Therefore, the development of MRT instability in (x, y) plane, or in (r,
will increase to over 1000 T. In this case, the growth rate of MRT instability for almost all perturbation wavelengths can be decreased to zero. Therefore, the development of MRT instability in (x, y) plane, or in (r, 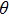 ) plane in cylindrical liner implosions can be nearly completely mitigated. However, in (x, z) plane the axial magnetic field is just several tens of Tesla. Hence, the growth rate in (x, z) plane cannot be reduced to zero, though largely mitigated by the axial magnetic field.
) plane in cylindrical liner implosions can be nearly completely mitigated. However, in (x, z) plane the axial magnetic field is just several tens of Tesla. Hence, the growth rate in (x, z) plane cannot be reduced to zero, though largely mitigated by the axial magnetic field.
The MRT instability developing initially on the outer surface may feed to the inner surface. The feedthrough factor F measures this effect of perturbation at one interface on the other interface.[16,21] The feedthrough can provide significant seeding at inner interface when the implosion is slowed down or Richtmyer–Meshkov (RM) instability is developed. The feedthrough is only related to the perturbation wavelength and the thickness when the magnetic field is zero with a simple form 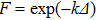 . Figure 6 shows that the feedthrough factor F increases with perturbation wavelength
. Figure 6 shows that the feedthrough factor F increases with perturbation wavelength 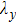 , where the gravity
, where the gravity  . We also find that the feedthrough is decreased in compressible condition compared to that in incompressible condition when the magnetic field is not zero.
. We also find that the feedthrough is decreased in compressible condition compared to that in incompressible condition when the magnetic field is not zero.
4. SummaryIn this paper the characteristics of MRT instability of liner plasmas in MagLIF is theoretically investigated. A three-region slab model, based on ideal MHD equations, is used to derive the dispersion relation of MRT instability. The effect of compressibility on the development of MRT instability is specially examined. It is shown that in the case of zero magnetic field, the growth rate in compressible assumption is approximately the same as that in incompressible assumption. However, the growth rate of MRT instability in compressible condition is generally lower than that in incompressible condition, because the magnetic field frozen in the plasma can provide stronger restoring force when the plasma is compressible. When the acoustic velocity 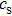 is small, this effect is more remarkable. When
is small, this effect is more remarkable. When 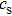 is large, the growth rate will approach that in incompressible condition. It is also shown that in the case of zero magnetic field, the growth rate monotonically decreases with perturbation wavelength. The presence of magnetic field can remarkably reduce the growth rate specially for short-wavelength perturbations. The growth rate of MRT instability in the (x, y) plane may be decreased to zero because the magnetic field can be increased to over 1000 T and completely mitigate the perturbations during liner implosions.
is large, the growth rate will approach that in incompressible condition. It is also shown that in the case of zero magnetic field, the growth rate monotonically decreases with perturbation wavelength. The presence of magnetic field can remarkably reduce the growth rate specially for short-wavelength perturbations. The growth rate of MRT instability in the (x, y) plane may be decreased to zero because the magnetic field can be increased to over 1000 T and completely mitigate the perturbations during liner implosions.
We also discuss the feedthrough of MRT instability of outer liner surface on inner surface perturbation. It is shown that in the case of zero magnetic field, the feedthrough factor depends on the perturbation wavelength and liner thickness, independent of compressibility or incompressibility condition. However, when the magnetic field is not zero, the feedthrough factor in compressible condition is generally much lower than that in incompressible condition, because the feedthrough factor also depends on the growth rate of MRT instability, which varies evidently between compressible and incompressible assumptions.