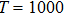† Corresponding author. E-mail:
We present the preliminary results of our code OPAQS (opacity calculation using quantum statistical model) that is based on the self consistent Hartree–Fock–Slater model for the average atom. The code is capable of performing robust calculations of average charge state, frequency-dependent and mean opacities. The accuracy of the atomic model is verified by comparing the calculations of average charge state with various published results. The monochromatic opacities for iron computed at different sets of temperatures and densities are compared with LEDCOP. The Rosseland and Planck opacities for iron and aluminum are validated with some state-of-the-art codes. The results are in good agreement with the published data.
Radiative properties provide us with insight about the behavior of the matter during its interaction with a radiation field. In astrophysics and environmental science, the more specific term used for referring to radiative properties is opacity: a measure of the resistance of matter to the transmission of radiation. There are various absorption and scattering mechanisms that impede the transmission and make the material opaque to radiation, such as photo-excitation, photo-ionization, inverse bremsstrahlung, and Thomson scattering. The experimental determination of opacity relies on transmission/absorption and emission spectroscopic techniques.[1–3] However, there are many practical situations in which measurements cannot be achieved in laboratory experiments, hence theoretical predictions of opacities are inevitable.[4]
Fast and accurate calculations of radiative properties are crucial for performing radiation hydrodynamic simulations and spectroscopic diagnostics in diverse research areas, such as stellar physics, inertial and magnetic confinement fusions. While modeling such problems, average charge state and photon absorption coefficient data must be available in the wide range of density and temperature. In this regard, extensive calculations need to be performed.[5–7] A few years back, these calculations were limited because of the limited capacity of the computers, so approximate atomic physics models were developed.[8–13] Significant advances in computational techniques have taken place, so with refined numerical methods and improved computational techniques now detailed and more complex approaches to opacity calculations are possible to implement.[14–17] However, due to the fast computational speed, the average models are still used widely where detailed calculations can be compromised.[1]
In thermodynamic equilibrium, free electrons follow the Maxwell–Boltzmann distribution, whereas the energy density distribution of photons is given by the Planck distribution. Our model is based on local thermodynamic equilibrium (LTE), which implies that at any particular instant, photon and electron distributions are in equilibrium with each other. From a computational point of view, LTE simplifies the calculations because instead of solving detailed rate equations, the atomic level populations can be found by Saha and Boltzmann equations, without requiring any fundamental cross section calculations.[18]
Many computational and experimental efforts are going on in parallel for achieving reliable opacities data.[1,7,19–32] It includes a large list, but here we are giving a short introduction to some of the sources, which we have used for comparison of our results. The opacity project (OP)[33] and opacity project at Livermore (OPAL)[34] have been the early sources of opacity data for astrophysicists since the nineties, and are still used extensively for modeling various problems in stellar physics.[1] OP is an online database in which atomic data is calculated using the R-matrix method, utilizing the close-coupling approximation.[33] OPAL code calculates the solution of the Schrödinger wave equation by applying relativistic analytical potential, and level populations are found by the minimization of the system’s free energy.[34] SCO-RCG is a hybrid code and combines detailed level and statistical approaches.[35] The most recent and widely tested code in the field of stellar physics is OPAS, which is based on LTE and performs calculations by combining detailed configuration and level accounting methods.[36] STA code interpolates smoothly between detailed configuration accounting and average-atom approach.[37] CASSANDRA code utilizes a detailed configuration method for obtaining atomic data and an ab-initio method for the computation of atomic physics, employing the Dirac–Hartree–Slater approximation.[38] CORONA code obtains atomic data from Perrot’s screened hydrogenic model, and average atom model in the Thomas–Fermi approach is used for average ionization.[39] LEDCOP code uses the relativistic self-consistent Hartree–Fock method, and ionic populations are calculated by using the Saha equation.[40] THERMOS code makes use of relativistic analytical potential in solving the Schrödinger equation, and calculates occupation numbers using an average atom model.[7]
The model presented in this paper is based on the average atom approximation. At high temperature (T > 10 eV), this approximation is widely used to describe the state of matter.[41] The self-consistent potential in the average atom model is calculated for an ion with average occupation numbers of energy levels, along with the free electrons in the charge-neutral spherical cell. The cross sections for radiative properties are used in the non-relativistic limits. The atomic model is mainly adopted from Ref. [7] with the exception that we have implemented the numerical scheme of Refs. [42] and [43] for the solution of the Schrödinger equation.
This paper provides the sketch of a near-future research program as much as reporting on the first steps. Some results of our model have been reported previously[44,45] in which calculations were validated with some of the advanced codes, and the results were also tested in radiation hydrodynamic code MULTI-2D.[46] In what follows, Section
In our calculations, it is assumed that a well-defined average atom can show the average behavior of all the atoms and ions at that temperature and density. This average atom is a fictitious atom with non-integral occupation numbers. It occupies a spherical cell in which a nucleus is present at the center and electrons are distributed around it following a radial distribution. The volume of the cell is defined by the mean volume per atom as
 |
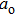
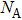
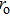
 |
After defining the atomic sphere, we solve the system of Hartree–Fock–Slater (HFS) equations for the self-consistent potential and wave functions. These calculations need the intra-atomic potential and distribution of electrons within the cell. We have taken these values from the Thomas–Fermi model[7] as the first guess. The HFS equations are given by
 |
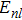
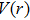
 |
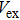
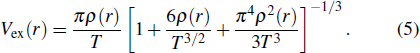 |
For the above equations to be solvable, the wave function must be separable. We have taken wave function 
 |
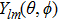
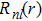

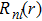
The radial electron density 
 |
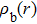
 |
The free electrons density 
 |
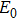
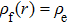
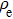
 |
 |
 |
Finally, the mean charge 
 |
Equations (
Once the average charge state, energy levels, and occupation numbers have been determined, the total frequency-dependent opacity 
 |
Photo-excitation coefficient 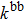
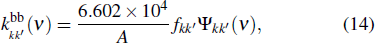 |
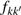
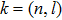

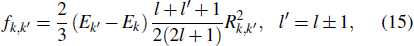 |
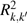

 |
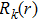
The 

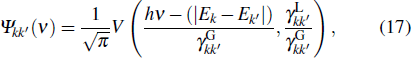 |
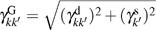
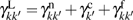
The standard formulas are used for natural 

 |
 |
Hydrogen-like approximation is used for both the fine structure width 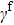

 |
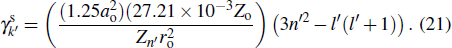 |
Electron collisional broadening 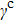
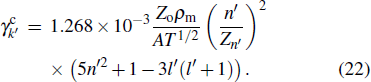 |
All broadening mechanisms are not equally likely, the dominance of any particular phenomenon takes place depending upon the plasma conditions.
The photo-ionization cross section is taken in the nonrelativistic approximation, calculated as
 |
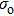
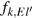
 |
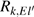
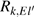
For inverse bremsstrahlung coefficient, the results of hydrogen atom are used[48]
 |
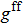
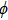
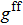
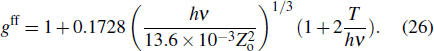 |
The degeneracy factor 
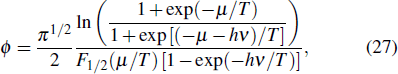 |
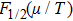
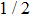
At high temperatures, the absorption cross sections for the above three processes fall to very low values, which causes a problem in numerical calculations for Rosseland mean (being the harmonic mean which diverges at very low values). Hence, scattering has to be added as the lower bound in the absorption coefficient to avoid numerical divergence.[2] Our model is currently capable of performing calculations in non relativistic limits only, so we have used Thomson scattering, which is the classical limit of Compton scattering (energy less than electron rest mass energy). It is classified as coherent scattering and given by
 |
The contributions determined from Eqs. (
The radiation hydrodynamic codes require the coupling of the radiation transfer equation (RTE) with the hydrodynamic equations. The frequency-dependent opacity 

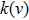

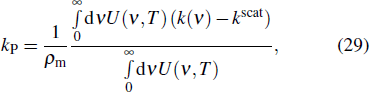 |
 |
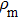
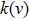
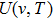
 |
Note that the Rosseland mean opacity is calculated by taking the harmonic average of the extinction coefficient (absorption + scattering), whereas the Planck mean opacity is obtained by the arithmetic mean of the total absorption coefficient (without scattering). The numerical scheme for the calculation of the mean opacities is adopted from Ref. [54].
By using the methodology given in the previous section, a computer code OPAQS has been developed for the calculation of the average charge state, monochromatic and mean opacities. A schematic flow diagram of the program is shown in Fig.
In order to determine the reliability of a computer code, comparison with available cutting-edge experimental measurements is necessary. In the case of unavailability of experimental data, alternate choice becomes a comparison with state-of-the-art theoretical models and computer codes. As we are intended to show the strengths and weaknesses of our model, so the main purpose of this section is to carry out the validation of the results computed with OPAQS. We have mainly benchmarked the results of OPAQS with LEDCOP, because of its availability and extensive use in research. However, comparison is also made with many other published results, wherever possible. In what follows, we have validated our results of radial wave function, average charge state, frequency-dependent and mean opacities.
The calculations of radial wave functions (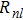

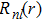

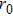
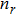
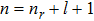

 | Fig. 2. (color online) The radial wave function    |
The degree of ionization is the most critical parameter in the calculations of atomic properties as it strongly influences many other plasma properties, such as pressure, conductivity, and opacity coefficients. Hence, it is a conventional practice to compare the average charge state (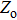

| Table 1.
Comparison of average charge state for aluminium plasma computed at density of 1 g/cc and temperatures of |
| Table 2.
Comparison of average charge state for germanium plasma computed at density of 0.01 g/cc and temperatures of T = 300 eV and T = 500 eV. . |
| Table 3.
Comparison of average charge state for iron plasma computed at different densities and temperatures. . |
The degree of ionization helps in analyzing the overall behavior of plasma at various plasma conditions. We have tested the effect of rise in temperature on the ionization state of plasma. The computation is performed for iron plasma at three different densities of 0.001 g/cc, 0.01 g/cc, and 0.1 g/cc. The results are shown in Fig.
 | Fig. 3. (color online) Average ionization of iron plasma versus temperature at densities of 0.001 g/cc, 0.01 g/cc, and 0.1 g/cc. |
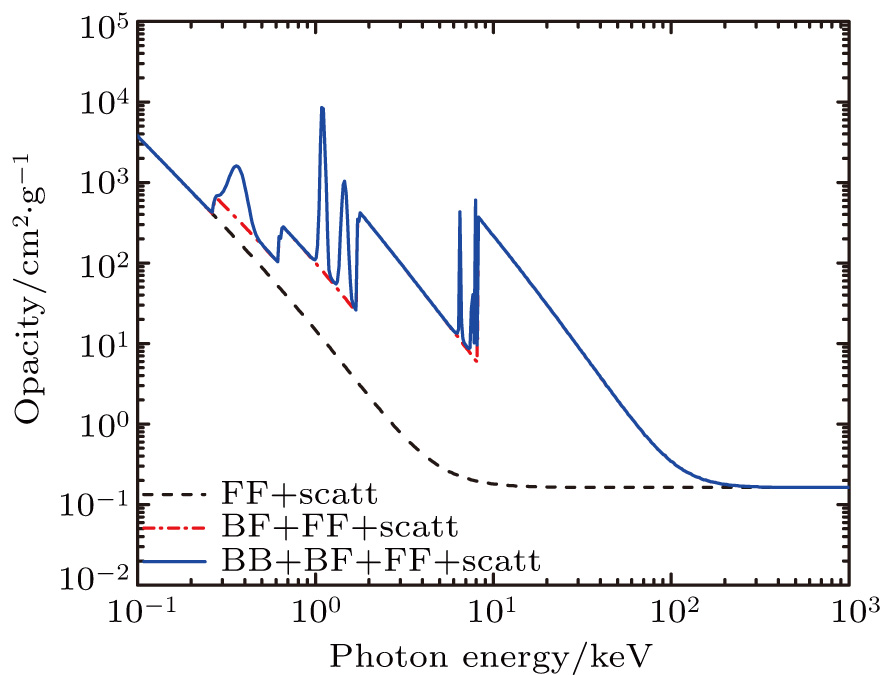
After verifying that the atomic model of OPAQS gives a correct degree of ionization, we proceed to test its calculations for radiative properties. The different contributions to opacity as a function of frequency are shown in Fig. 
For opacity validation, a graphical comparison between OPAQS and LEDCOP is presented in Fig.
Once the behavior of the frequency dependent opacity is tested, the next step is to validate its average behavior, i.e., the Rosseland and Planck mean opacities. The validation of the mean opacities is necessary as they serve as input parameters in radiation transfer computations. We have calculated the mean opacities for the same conditions of iron plasma and presented them in Table
| Table 4.
Comparison of Rosseland, Planck mean opacities and average charge state for iron at density of 1 g/cc and different temperatures. . |
Despite the good comparison of average charge state, OPAQS gives slightly higher values of opacities than those with detailed models, which is also reported elsewhere.[56] The maximum difference in Rosseland mean opacity calculation is found to be 17% at 800 eV, for Planck opacity it is 25% at 250 eV, whereas the maximum deviation in average charge state is 1.5% at 250 eV. In the literature, even the sophisticated codes have reported differences up to 300% in monochromatic opacities[36,57] and up to 60% in Rosseland mean opacities.[58] The reason for these deviations can be justified as follows. The Rosseland mean is a harmonic mean and it depends upon many factors such as features of spectrum (photo-ionization edges, line shapes, and valleys among peaks), numerical methods used in averaging, the grid points, etc. So to get an exact match among the codes or with the experimental data is indeed a challenging task for the theoretical researchers.
In Tables
| Table 5.
Rosseland mean opacity computed for aluminium plasma at density of 1 g/cc and different temperatures. Values are taken from Ref. [47] for comparison. . |
| Table 6.
Rosseland mean opacity computed for iron plasma at 1 g/cc density and different temperatures. Values are taken from Ref. [47] for comparison. . |
We have also compared the calculations of mean opacities with some other state-of-the-art opacity codes being frequently used in the field of stellar physics: STA, OP, CASSANDRA, OPAS, SCO-RCG, and LEDCOP.[59] Comparison is shown in Table
| Table 7.
Planck and Rosseland mean opacities computed for iron plasma at density of 3.4 mg/cc and different temperatures. Values are taken from Ref. [59] for comparison. . |
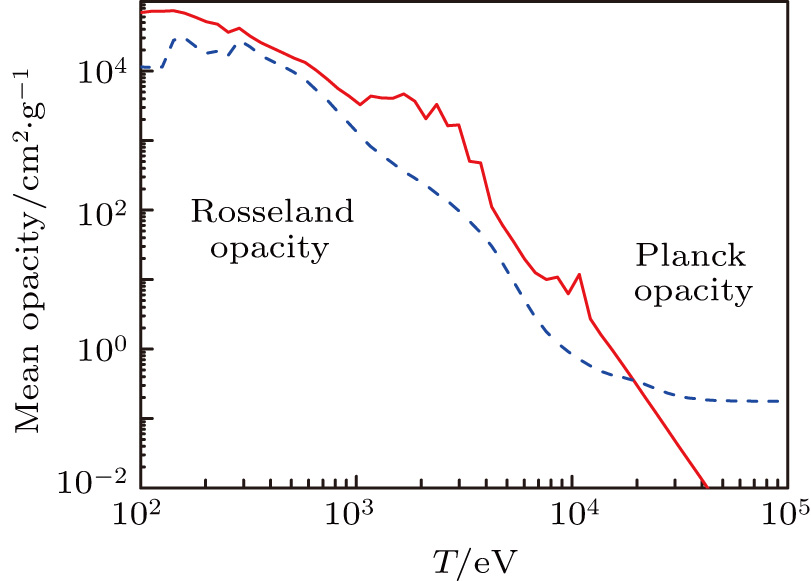
We have also tested the temperature dependence of the mean opacities, and the result is shown in Fig.
We have developed a new opacity code OPAQS that is based on the average atom model and performs calculations using quantum statistical approach. The code is capable of performing robust calculations of average charge state, frequency-dependent opacities along with grey/mean opacities. The results are compared with available published data on every single step to make sure of the correctness of the calculations. The code is reliable and its frequency-dependent as well as mean opacities show very good agreement with LEDCOP for given plasma conditions. The small discrepancy is due to different approaches employed in both codes.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] |