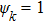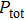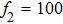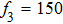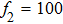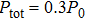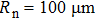† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11674074) and the Program for Changjiang Scholars and Innovative Research Team in University, China (Grant No. IRT1228).
The acoustical scattering cross section is usually employed to evaluate the scattering ability of the bubbles when they are excited by the incident acoustic waves. This parameter is strongly related to many important applications of performance prediction for search sonar or underwater telemetry, acoustical oceanography, acoustic cavitation, volcanology, and medical and industrial ultrasound. In the present paper, both the analytical and numerical analysis results of the acoustical scattering cross section of a single bubble under multi-frequency excitation are obtained. The nonlinear characteristics (e.g., harmonics, subharmonics, and ultraharmonics) of the scattering cross section curve under multi-frequency excitation are investigated compared with single-frequency excitation. The influence of several paramount parameters (e.g., bubble equilibrium radius, acoustic pressure amplitude, and acoustic frequencies) in the multi-frequency system on the predictions of scattering cross section is discussed. It is shown that the combination resonances become significant in the multi-frequency system when the acoustic power is big enough, and the acoustical scattering cross section is promoted significantly within a much broader range of bubble sizes and acoustic frequencies due to the generation of more resonances.
Gas bubbles play an important role in the generation, scattering, and absorption of sound in a liquid. The acoustical scattering cross section is usually employed to evaluate the scattering ability of the bubbles, and is defined as the square of the ratio between the amplitude of the radiated spherical wave by bubbles and the amplitude of the incident acoustic wave. Compared with the scattering behavior of incompressible objects, the acoustical scattering cross section of bubbles is quite significant due to the compressible nature of the gases inside the bubbles, and the scattering cross section of bubbles under acoustic excitation can be of the order of 1000 times of its own geometrical cross section.[1,2]
The acoustical scattering cross section of gas bubbles has been studied over several decades. Linear models of bubble scattering cross sections are used to measure oceanic bubble size distributions and predict their acoustic effects, with applications involving sonar performance,[3,4] and surf zone or subsurface acoustics.[5,6] A paper by Ainslie[1] has reviewed expressions and definitions in the literature for acoustical cross sections, resonance frequencies, and damping factors of a spherically pulsating gas bubble in an infinite liquid medium. The survey of bubble scattering models can be ordered into three threads, referred to as the “Wildt” thread, the “Devin” thread, and a third “nonlinear” thread. Zhang also proposed a generalized equation for the scattering cross section of spherical gas bubbles oscillating in liquids under acoustic excitation.[7] Shi et al. studied the oscillation properties influenced by stimulated sound scattering processes.[8] For the cases of bubble clouds, both the velocity and amplitude of the acoustic waves will be modulated due to the presence of bubbles. Similarly, the velocity and amplitude of the spherical waves generated by the oscillating bubbles will also be changed by the other bubbles.[9] For the linear case, Commander and Prosperetti[10] performed a systematic theoretical study. For a spherical bubble cloud, the acoustical scattering cross section could be theoretically calculated following the framework of d’Agostino and Brennen.[11]
The previous investigations detailed in the literature mainly focused on the case of single-frequency acoustic excitation. However, to promote acoustic effects in many application areas, the multi-frequency approach (i.e., waves with two or three, even more acoustic components) could be an effective method.[12] The multi-frequency approach has been employed to measure the bubble density in water,[13–15] find the bubble size distributions with void fraction in the ocean,[16,17] optimize the scattering from a micro bubble at a frequency different from the driving,[18] and advance the biomedical ultrasound imaging techniques.[19] Zhang et al. focused on the dual-frequency approach to obtain the influence of mass transfer on the oscillations of cavitation bubbles, and proposed a threshold of acoustic pressure amplitude dividing the bubble response into two regions.[20] Furthermore, Zhang et al. studied the acoustical scattering cross section, and the combination and simultaneous resonances of gas bubbles under dual-frequency acoustic excitation in detail.[21–23]
However, the problems of acoustical cross section of a bubble under multi-frequency excitation are still poorly investigated in the literature. The motivation of this paper is to achieve a much broader range of acoustical scattering cross section by the multi-frequency approach. Different from the work of Zhang et al.,[21–24] our work improves the dual-frequency approach to the multi-frequency approach. The main aim of the paper is to obtain directly the analytical solution of the acoustical scattering cross section under multi-frequency excitation, and make a comprehensive analysis of the influence of several paramount parameters (e.g., bubble equilibrium radius, acoustic pressure amplitude, and acoustic frequencies) in the multi-frequency system.
The remainder of the article is organized as follows. In Section
The dynamics of spherical gas bubbles in Newtonian, compressible, and viscous liquids are considered, and the equation of bubble motion can be written as the Keller–Miksis equation[25,26]
 |
 |
 |
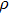
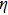
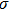
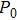

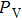
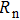
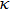
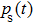
For multi-frequency excitation, 
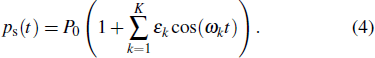 |
Assume the amplitudes of the acoustic wave as 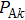





The radiation pressure at radial coordinate r from the origin of the bubble center can be given as[27]
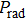


 |
Here, B/r is the amplitude of the divergent spherical scattered wave generated by the bubble oscillations. Following the definition proposed by Wildt,[2] the acoustical scattering cross section (
 |
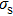
The analytical solution for the acoustical scattering cross section under multi-frequency acoustic excitation is obtained in this section. The solution of the Keller–Miksis equation under multi-frequency acoustic field can be expressed as
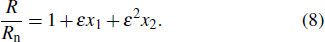 |
Thermal damping is ignored. Substituting Eq. (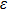
 |
The sum of all terms with order 
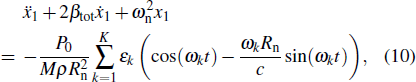 |
 |
 |
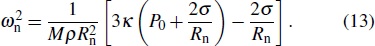 |
The solution of Eq. (
 |
 |
 |
Here, 



 |
The typical parameters for a bubble in water, as used in the calculations with the Keller–Miksis model, are 










For comparison, the total input power should be a constant during simulations of different cases, so we can obtain the acoustic pressure amplitude during different cases
 |
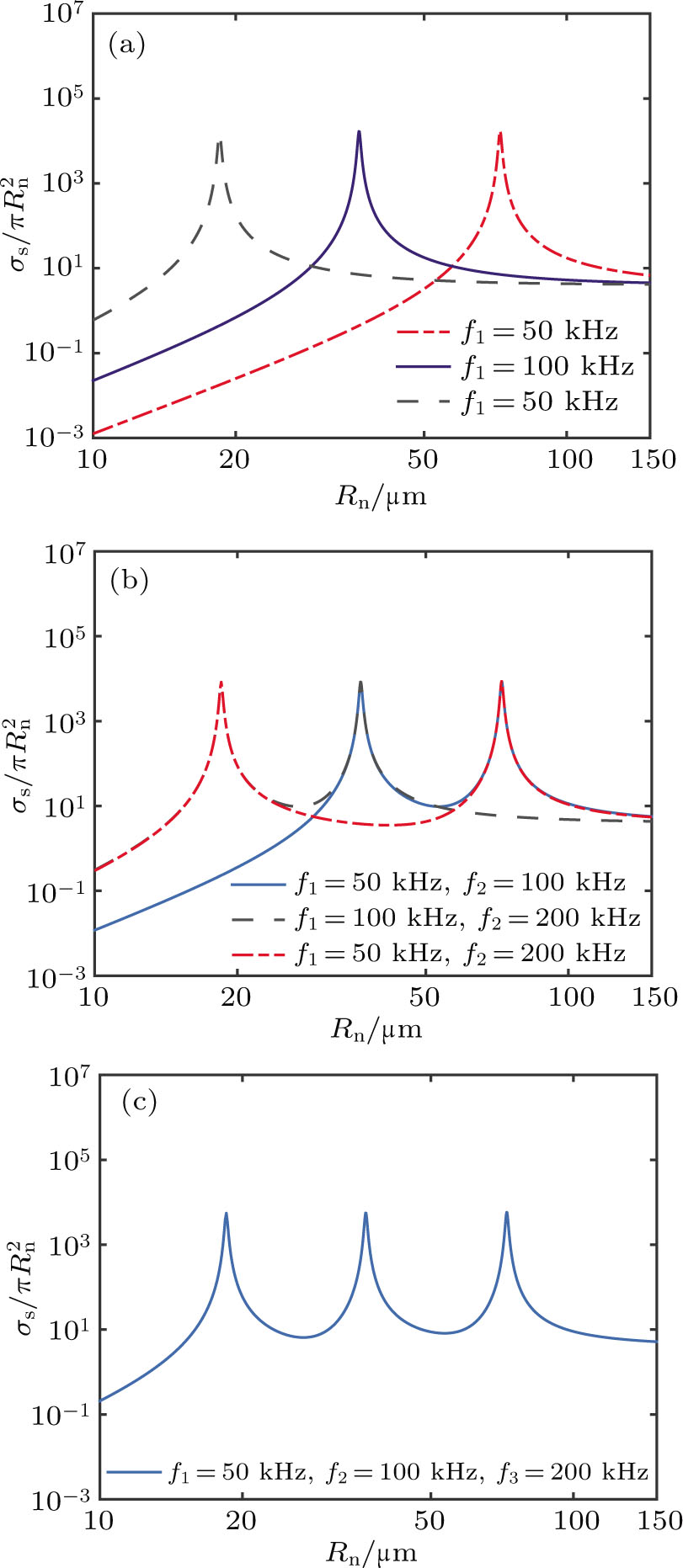
Figure 




Next, the numerical solution is employed to study the acoustical scattering cross section generated by bubble oscillations. The Keller–Miksis equation can be reformulated as a set of autonomous differential equations of first order
 |
 |

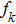
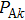
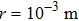
In this section, demonstrating examples of radiation pressure and acoustical scattering cross section generated by an oscillating bubble under multi-frequency acoustic excitation within a wide range of parameters are shown. The nonlinear characteristics and influential parameters of the acoustical cross section are discussed in detail.
Figure 



Figure 
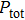



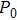
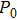
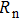

It is shown that the harmonics and subharmonics increase when driving the bubbles stronger in the case of single-frequency acoustic excitation. With the increase of 
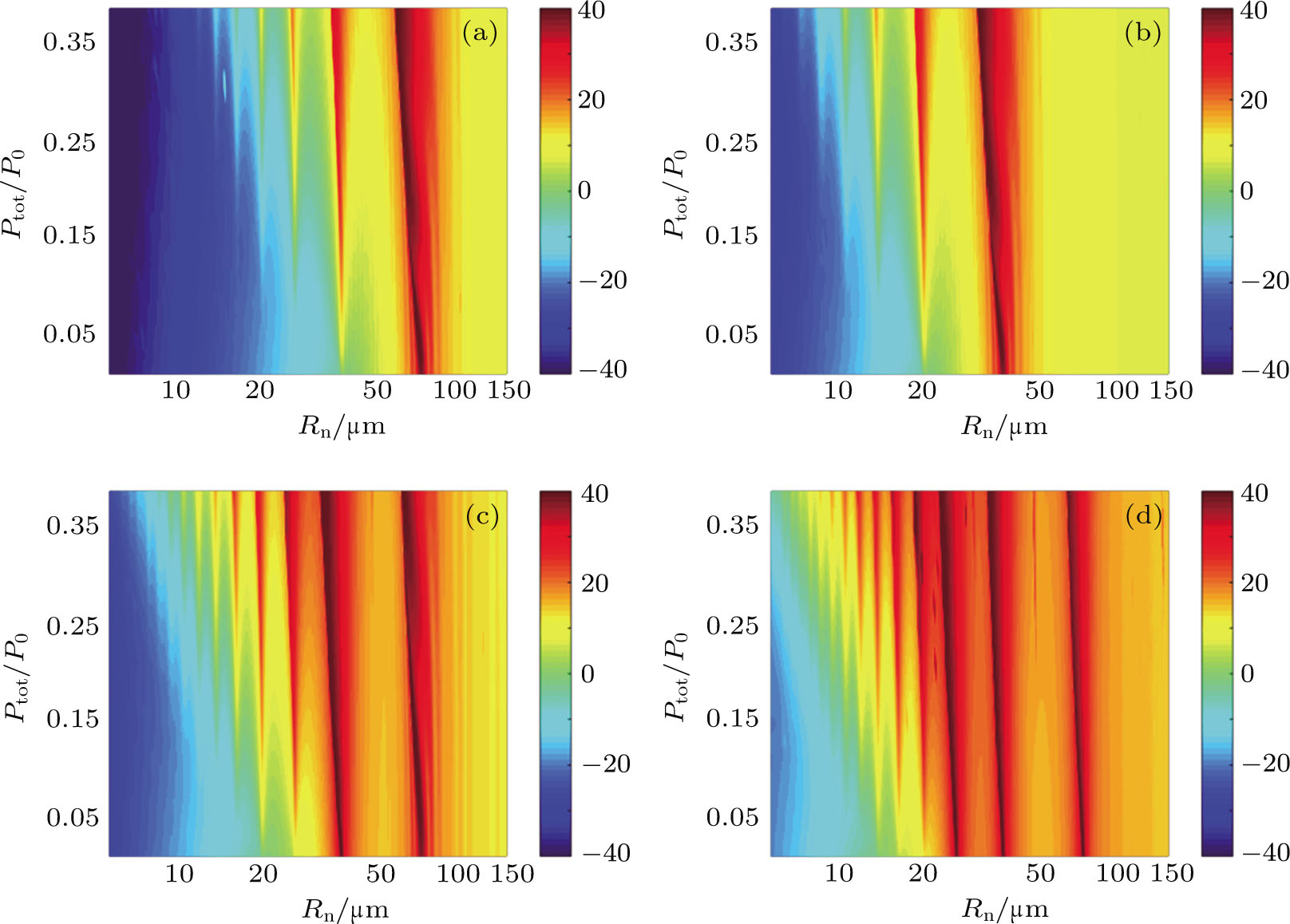
Figure 

Figure 




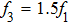
In the case of single-frequency excitation, for a certain acoustic pressure amplitude 
Figure 

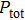
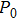


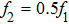

Compared to the single-frequency approach, for a certain bubble radius 

Both the analytical and numerical solutions of the acoustical scattering cross section of a bubble under multi-frequency excitation are obtained. The prediction of the scattering cross section by the analytical method can give the main resonances clearly, but cannot predict complex nonlinear phenomena when 
The nonlinear characteristics of the scattering cross section under the multi-frequency approach are investigated numerically by using parameter space diagrams (


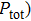
The influence of several paramount parameters in the multi-frequency system on the scattering cross section has been discussed. Due to the vast parameter space, the properties of the scattering cross section are still not fully explored. Meanwhile, a large parameter zone is involved, leading to great difficulties for the design. So optimization of the multi-frequency approach is still needed and worth studying.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] |