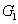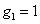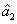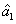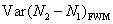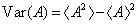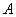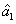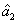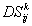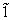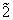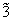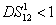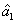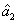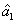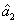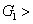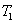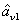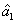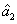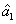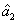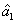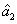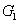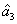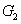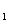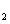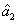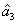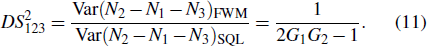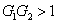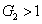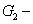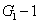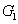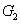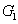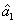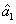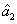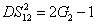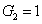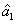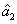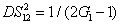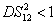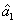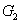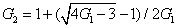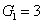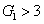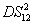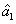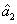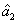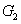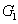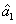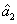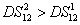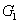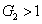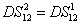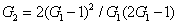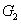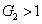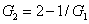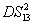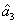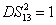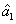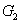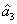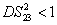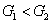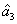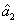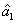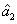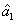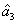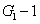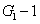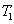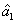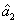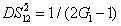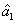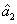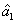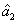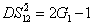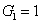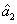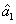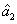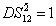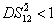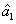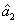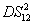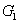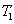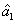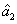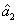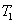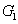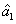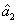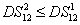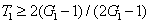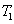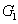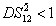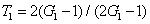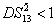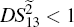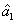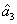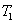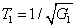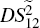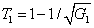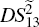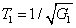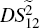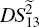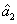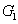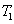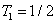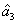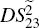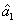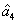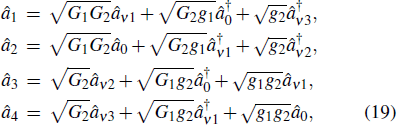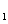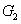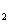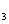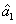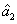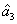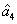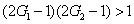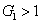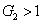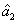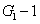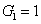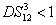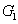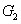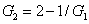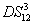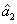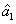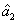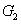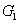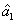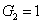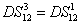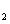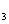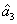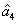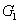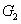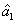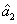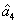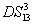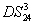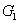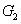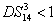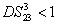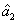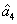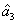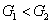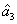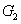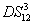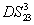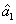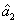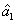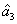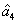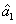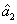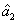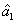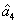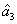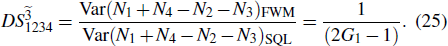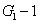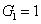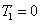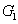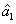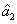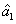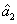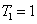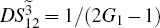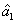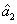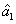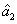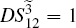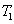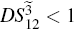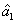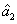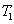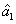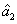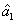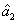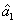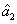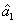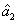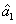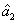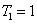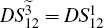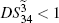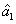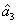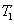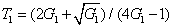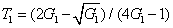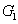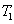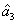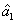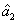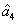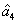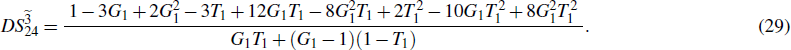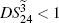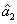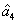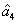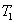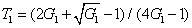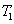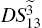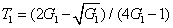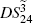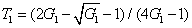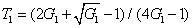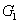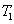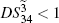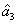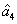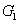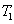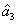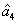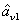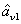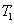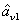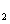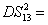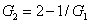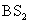Characterization of the pairwise correlations in different quantum networks consisting of four-wave mixers and beamsplitters
1. IntroductionQuantum correlations shared between the multiple quantum correlated beams are the fundamental ingredients of the most continuous-variable (CV) quantum technologies.[1,2] The pairwise correlations (PCs) involved in the multiple quantum correlated beams are an important research subject. For example, Refs. [3], [4] and Ref. [5] gave the classification of three-qubit correlation and four-qubit correlation respectively, which both involve the consideration of PCs. Therefore, the quantum correlation shared by any pair of the multiple quantum correlated beams is worth studying. In recent years, four-wave mixers (FWMs) based on a hot rubidium vapor[6–21] have been proved to be very successful for many practical implementations, for example, tunable delay of Einstein–Podolsky–Rosen entangled states,[9] low-noise amplification of entangled states,[10] quantum mutual information,[13] and SU(1,1) interferometer[22,23] have been experimentally realized. In 2014, our group has experimentally realized the quantum correlated triple beams by cascading two FWM processes (FWM + FWM network) and strong relative intensity squeezing has been observed between the generated triple beams.[24] Reference [25] presents a scheme to realize the versatile quantum networks by cascading several FWM processes in warm rubidium vapors, and Refs. [26] and [27] discuss the tripartite entanglement and correlation in the cascaded FWM processes, but the PCs with quantum correlation are not compared between the FWM + FWM network and the FWM+beamsplitter (BS) network, let alone the quantum correlation recovery and enhancement of the PCs. However, in this paper, it can be found that the PCs with quantum correlation can be enhanced compared with the one of the single FWM process in the FWM+BS network. Therefore, we study the PCs[28–30] in different quantum networks, such as FWM + FWM, FWM+BS, FWM + FWM + FWM, and FWM + BS + BS networks. In addition, the repulsion effect phenomena between the PCs with quantum correlation are present in the FWM + FWM and FWM + FWM + FWM networks instead of the FWM+BS and FWM+BS+BS networks. This gives the prediction that signal (idler)–frequency mode cannot be quantum correlated with the other two idler (signal)–frequency modes simultaneously.
This article is organized as follows. In Section 2, we describe the quantum correlation performance of the FWM (BS) network using the degree of relative intensity squeezing (DS) criterion. In Section 3, we use the DS criterion to analyze the PCs existing in the FWM + FWM and FWM+BS networks. In Section 4, we analyze the PCs existing in the FWM + FWM + FWM and FWM+BS+BS networks. In Section 5, we give a brief summary of this paper.
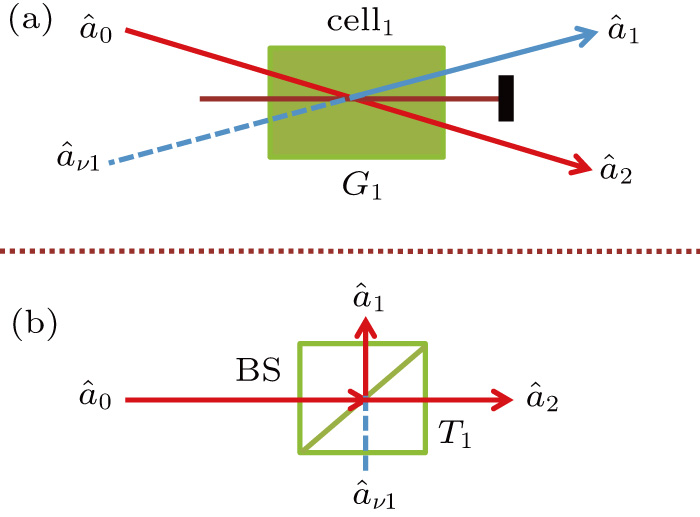
2. FWM (BS) networkIn this section, we give a simple description of the FWM (BS) network. Firstly, we will focus on the FWM network. FWM is a nonlinear process which converts two pump photons into a probe photon and an idler photon. In the cell of Fig. 1(a), an intense pump beam and a much weaker signal beam (
of Fig. 1(a), an intense pump beam and a much weaker signal beam ( ) are crossed in the center of the rubidium vapor with a slight angle. Then the signal beam is amplified as
) are crossed in the center of the rubidium vapor with a slight angle. Then the signal beam is amplified as  and a new beam called idler beam is generated as
and a new beam called idler beam is generated as  on the other side of the pump beam at the same time. The signal beam and idler beam have different frequencies. The input–output relation of the FWM process shown in Fig. 1(a) is given by
on the other side of the pump beam at the same time. The signal beam and idler beam have different frequencies. The input–output relation of the FWM process shown in Fig. 1(a) is given by
where

is the power gain in the FWM process and
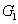
-
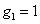
,
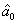
is the coherent input signal and
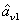
is the vacuum input,
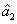
is the amplified signal beam and
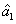
is the generated idler beam. See Ref. [
6] for details. The relative intensity fluctuations
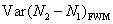
can be given by
where
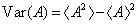
denotes the variance of
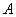
. The standard quantum limit (SQL) for the twin beams can be given bys
The PC with quantum correlation between the twin beams
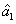
and
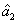
can be quantified using
DS criterion, which is the ratio of the variance of the relative intensity for the twin beams to the variance at the SQL, namely
where the superscript and subscript for the
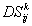
represent the network (we have three networks throughout the whole discussion, i.e., FWM (BS) network: 1 (
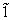
), FWM + FWM (BS) network: 2 (
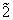
), FWM + FWM (BS)+FWM (BS) network, 3 (
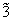
)), the
ith (
i = 1, 2, 3) beam, and the
jth (
j = 2, 3, 4) beam in the network. The PC with quantum correlation of the twin beams from the FWM process can be demonstrated when
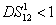
and can be easily obtained in the experiment since

is always larger than 1. However, the values of
DS of the individual beams
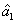
and
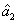
are given by
This corresponds to a linear increase in the noise on both the signal and idler beams as gain is increased. Thus the twin beams
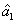
and
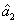
in the FWM process are both in thermal states. Equations (
4) and (
5) demonstrate that the PC with quantum correlation for the twin beams is present at the expense of increasing the fluctuations in the individual beams when
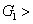
1.
Secondly, for the BS network in Fig. 1(b), the input–output relationship can be given by
where
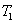
is the transmission of the BS.

is the coherent input signal and
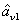
is the vacuum input. The values of
DS of the individual beams
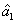
and
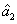
are given by
The
DS between the beams
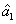
and
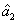
can be given by
As we can see from Eq. (
8), the
DS between the beams
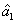
and
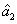
is independent of the transmission of the BS, thus equation (
8) represents the correlation level between the two beams in both the coherent states or one beam in the coherent state, the other in the vacuum state. Equations (
4) and (
8) demonstrate that the PC with quantum correlation cannot be obtained by BS with a coherent state and a vacuum state inputs due to its passive nature and the FWM process with
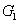
=1 is equivalent to the BS with

.
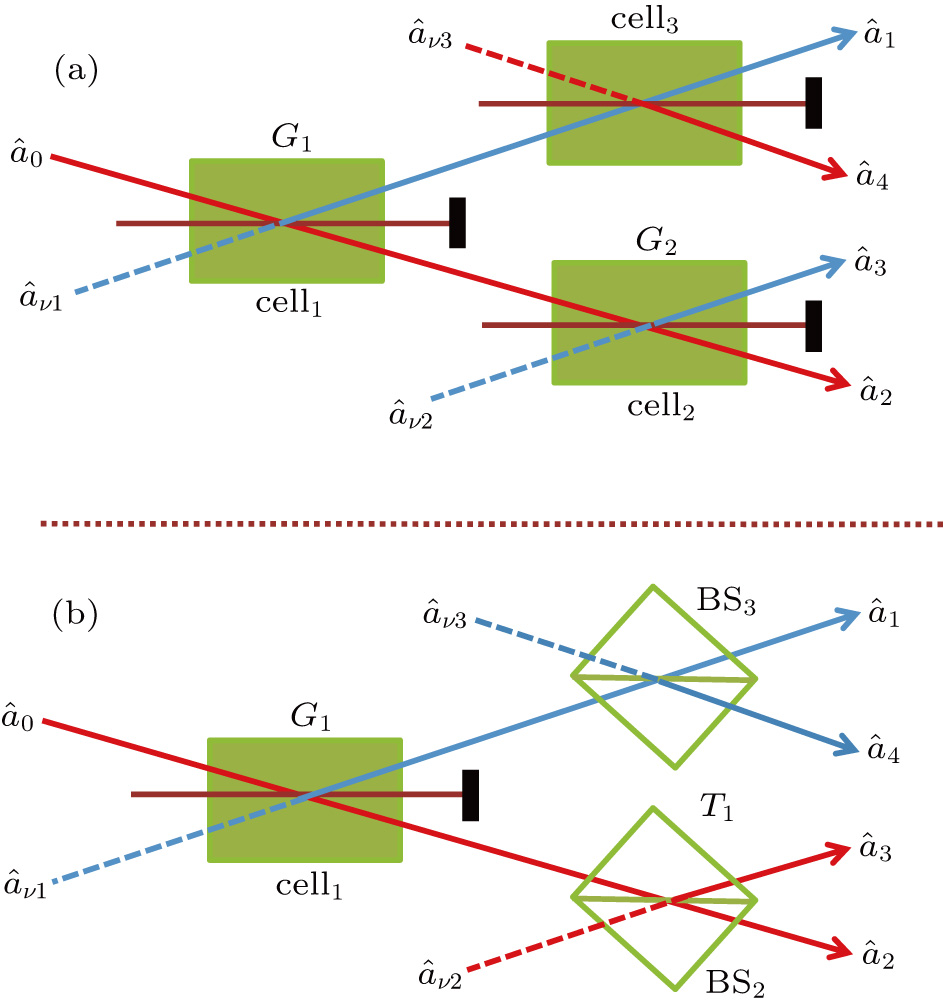
3. FWM + FWM (BS) networkIn this section, we analyze the network in which one of the twin beams is amplified or attenuated by one FWM or BS, respectively. Here the FWM and BS can be considered as the gain beamsplitter[21] or lossy beamsplitter, respectively. Firstly, we will focus on the FWM + FWM network. We take the signal beam from the first FWM process (cell ) as the seed for the second FWM process (cell
) as the seed for the second FWM process (cell ) in Fig. 2(a).[24]
) in Fig. 2(a).[24] ,
,  , and
, and 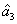 are the triple newly-generated beams in the output stage of the FWM + FWM network. In our previous work,[24] we have shown the generation of strong quantum correlation between the triple bright beams but not the PCs with quantum correlation for any pair of the triple beams. Here we will study all the possible PCs of the triple beams
are the triple newly-generated beams in the output stage of the FWM + FWM network. In our previous work,[24] we have shown the generation of strong quantum correlation between the triple bright beams but not the PCs with quantum correlation for any pair of the triple beams. Here we will study all the possible PCs of the triple beams  ,
,  , and
, and  in Fig. 2(a). The input–output relationship of the FWM + FWM network in Fig. 2(a) can be written as
in Fig. 2(a). The input–output relationship of the FWM + FWM network in Fig. 2(a) can be written as
where

and
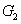
are the power gains for the cell
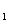
and cell
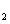
, respectively. It should be noted that the
DS of the triple beams (

,
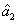
, and
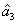
) is given by
Compared to Eq. (
4), equation (
11) means that the FWM + FWM network can enhance the quantum correlation of the system. The quantum correlation shared by the triple beams is present if
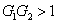
, i.e.,

or
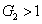
.
PC between 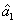 and
and  can be quantified by
can be quantified by
Equation (
12) will be reduced to 2
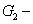
1 and 1/(2
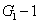
) when we set
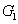
=1 and
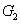
=1 respectively, corresponding to the cases of Eq. (
5) and Eq. (
4) respectively. The physical meaning is as follows. When we set
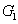
=1, the PC between the thermal states
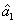
and

translates into the one between the vacuum state
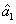
and the thermal state
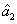
, i.e.,
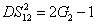
. When we set
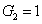
, the PC between the thermal states
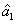
and
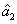
translates into the one between the twin beams from the first FWM process, i.e.,
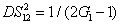
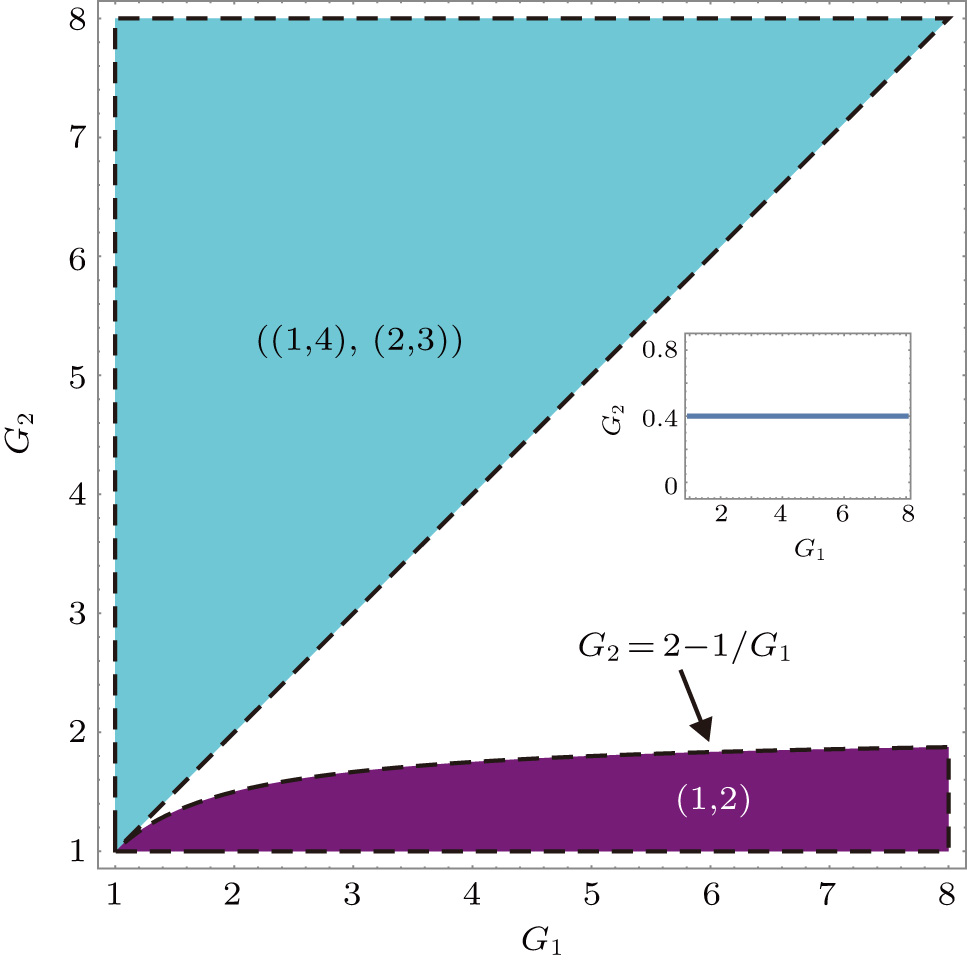
. The region in which
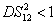
, i.e., there exists quantum correlation between the beams
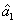
and

, is shown in purple denoted as (1, 2) in Fig.
3. The value of
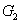
on the boundary (see the boundary given by
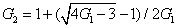
in Fig.
3) of that region reaches its maximal value of 1.33 when
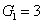
, and it decreases when
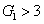
and will eventually reach the value of 1. The study of
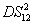
presented above is actually the question of how to preserve or even enhance the quantum correlation between the beams
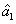
and
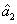
compared with the one between the twin beams from the first FWM process under the introduction of a gain beamsplitter which brings the deterioration effect to the quantum correlation by the quantum amplification of one of the beams (
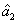
). The results shown in Fig.
3 actually show the value of
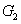
on the boundary below which the quantum correlation can always be preserved as the value of
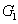
increases. More interestingly, in this network, the PC with quantum correlation between the beams
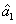
and
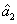
cannot be quantum recovered to the one between the twin beams from the first FWM process, i.e.,
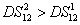
for any value of
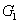
,
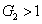
due to the quantum amplification from the gain beamsplitter. The condition of
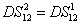
is given by
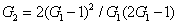
as shown in the inset of Fig.
3. With the increasing of

, the value of
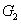
always increases and eventually saturates at the value of 1, but
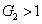
is required for the generation of the triple quantum correlated beams. That is to say, quantum amplification of the signal beam of the twin beams can destroy the quantum correlation between the twin beams inevitably.
PC between  and
and  can be quantified by
can be quantified by
Equation (
13) is equal to 1 when
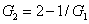
. Except that,
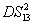
is always larger than 1, i.e., there is no quantum correlation between the beams

and
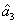
. The region in which
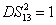
(

) is shown as the red line denoted as (1, 3) in Fig.
3. In this sense, there is no quantum correlation between the beams
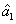
and

for any value of

and
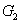
since

is always more than or equal to 1.
PC between  and
and 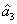 can be quantified by
can be quantified by
The region in which
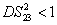
(
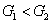
) is shown in cyan denoted as (2, 3) in Fig.
3. Therefore, the PC with quantum correlation between the beams

and

will be present for any

. This is not difficult to figure out if one looks at the functional form of Eq. (
14). In the region

, the existence of quantum correlation between the beams

and
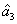
eliminates the possibility of the one between the beams
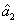
and
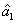
. In other words, beam
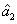
cannot be quantum correlated with beams
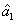
and

in the same gain region. In this sense, we could call this phenomena repulsion effect of quantum correlation between the PCs in the FWM + FWM network.
Secondly, for the FWM+BS network in Fig. 2(b), the DS of the triple beams is given by
Compared to Eq. (
11), this network cannot enhance the quantum correlation existing in the triple beams

,

, and
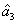
in Fig.
2(b). We will also analyze all the possible PCs.
PC between  and
and  can be quantified by
can be quantified by
Equation (
16) will be reduced to 1/(2
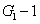
), 2
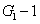
, and 1 when we set
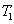
=1,
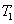
=0, and

=1 respectively, corresponding to the cases of Eq. (
4), Eq. (
5), and Eq. (
8) respectively. These phenomena can be understood as follows. When we set
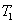
=1, the PC between the thermal states
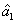
and
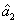
translates into the one between the twin beams from the first FWM process, i.e.,
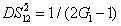
. When we set

, the PC between the thermal states
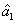
and
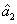
translates into the one between the thermal state
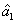
and the vacuum state
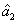
, i.e.,
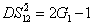
. When we set
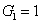
, the PC between the thermal states

and
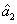
translates into the one between the vacuum state
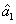
and the coherent state
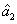
, i.e.,
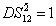
. This theoretical result is consistent with Eq. (
5) in Ref. [
31]. The region in which
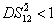
, i.e., there exists quantum correlation between the beams
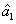
and
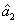
, is shown in green denoted as (1, 2) in Fig.
4(a). Different from the boundary of the
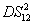
, with the increasing of
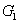
, the value of
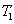
on the boundary always increases and eventually saturates at the value of 1 (see the boundary given by

in Fig.
4(a)). The study of

presented above is actually the question of how to preserve or even enhance the quantum correlation between the beams
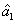
and
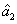
compared with the one between the twin beams under the introduction of a lossy beamsplitter which brings the deterioration effect to the quantum correlation by the attenuation of one of the beams (
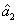
). The results shown in Fig.
4(a) actually show the value of
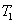
on the boundary above which the quantum correlation can always be preserved as the value of
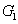
increases. More interestingly, in this case, the PC with quantum correlation between the beams
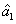
and
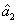
can be quantum recovered and enhanced compared with the one between the twin beams from the first FWM process, i.e.,
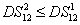
, when
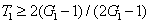
. The results shown in Fig.
4(a) actually shows the boundary (the red line in Fig.
4(a)) for the values of
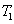
above which the quantum correlation enhancement can always be realized as the value of
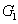
increases. That is to say, certain attenuation of the signal beam of the twin beams can recover and enhance the quantum correlation between the twin beams from the first FWM process.
PC between  and
and  can be quantified by
can be quantified by
The region in which
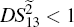
, i.e., there exists quantum correlation between the beams
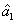
and
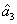
, is shown in magenta denoted as (1, 3) in Fig.
4(b). With the increasing of

, the value of
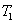
on the boundary always decreases and eventually reaches the value of 0 (see the boundary given by
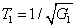
in Fig.
4(b)). As shown in Fig.
4, the sum of the boundary value of the
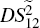
, i.e.,
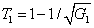
, and the boundary value of
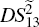
, i.e.,
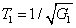
, is always equal to 1. That is to say, the PCs with quantum correlation between
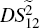
and
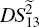
is limited by the lossy beamsplitter. In addition, the crossing region of

and

is present in Figs.
4(a) and
4(b), which means that the repulsion effect is absent for the FWM+BS network.
PC between 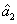 and
and  can be quantified by
can be quantified by
which is equal to 1 when
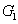
=1 or
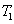
=1/2. As we all know, in order to generate the SQL, the shot noise limited beam, such as coherent state beam, is always preferred as shown in Eq. (
8).
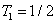
means that the balanced differential measurement of a thermal state can also obtain the SQL. Except that,

is always larger than 1, i.e., there is no quantum correlation between the beams

and
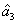
for any value of

and

, since
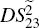
is always more than or equal to 1.
As Section 3 mentioned, the FWM (gain beamsplitter) will inevitably destroy the quantum correlation between the twin beams  and
and  from the first FWM process, while BS (lossy beamsplitter) can preserve or even enhance the quantum correlation between the twin beams
from the first FWM process, while BS (lossy beamsplitter) can preserve or even enhance the quantum correlation between the twin beams 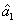 and
and  . The repulsion effect between the PCs with quantum correlation is predicted in the gain beamsplitter case (FWM + FWM network) instead of the lossy beamsplitter case (FWM+BS network).
. The repulsion effect between the PCs with quantum correlation is predicted in the gain beamsplitter case (FWM + FWM network) instead of the lossy beamsplitter case (FWM+BS network).
4. FWM + FWM (BS)+FWM (BS) networkIn this section, we analyze the network in which both of the twin beams are amplified or attenuated by two FWMs or BSs respectively. Here the FWM and BS can also be considered as the gain beamsplitter and lossy beamsplitter, respectively. Firstly, we will focus on the FWM + FWM + FWM network. We take the signal beam from the first FWM process (cell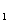 ) as the seed for the second FWM (cell
) as the seed for the second FWM (cell ) and the idler beam as the seed for the third FWM (cell
) and the idler beam as the seed for the third FWM (cell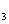 ) in Fig. 5(a).
) in Fig. 5(a).  ,
,  ,
,  , and
, and 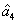 are the quadruple newly-generated beams in the output stage of the FWM + FWM + FWM network. The input–output relationship of the FWM + FWM + FWM network in Fig. 5(a) can be written as
are the quadruple newly-generated beams in the output stage of the FWM + FWM + FWM network. The input–output relationship of the FWM + FWM + FWM network in Fig. 5(a) can be written as
where

is the power gain of cell
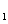
and
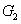
is the power gain of the cell
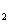
and cell
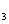
. It should be noted the
DS of the quadruple beams (
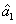
,
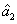
,
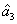
, and
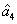
) is given by
Compared to Eq. (
11), this network has also enhanced the quantum correlation of the system. The quantum correlation shared by the quadruple beams is present if
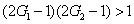
, i.e.,
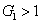
or
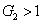
. Next let us analyze all the possible PCs in this network.
PC between  and
and 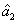 can be quantified by
can be quantified by
Equation (
21) will be reduced to 2

and 1/(2
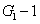
) when we set
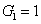
and

respectively, similar to the case of Eq. (
12). The region in which
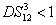
is shown in purple denoted as (1, 2) in Fig.
6. With the increasing of
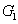
, the value of
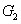
on the boundary always increases and eventually saturates at the value of 2 (see the boundary given by
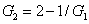
in Fig.
6). The study of
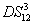
presented above is actually the question of how to preserve or even enhance the quantum correlation between the beams

and
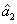
under the introduction of two gain beamsplitters which bring the deterioration effect to the quantum correlation by the quantum amplification of both of the beams (
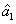
and
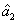
). The results shown in Fig.
6 actually show the boundary for the values of
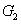
below which the quantum correlation can always be preserved as the value of
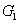
increases. More interestingly, in this case, the PC with quantum correlation between the beams
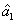
and

can be quantum recovered to the one between the twin beams from the first FWM process only when
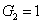
(the inset of Fig.
6), i.e.,
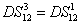
. But it means that the generation of the quadruple quantum correlated beams is impossible due to the absence of the cell
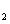
and cell
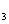
. That is to say, the quantum correlation recovery and enhancement are impossible for the FWM + FWM + FWM network.
PC between  and
and 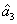 (
( and
and 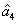 ) can be quantified by
) can be quantified by
Equation (
23) is always larger than 1 for any value of
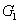
and
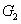
. In this sense, there is no quantum correlation between the beams
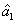
and

(
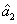
and
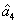
), since
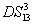
(
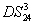
) is always larger than 1 for any value of
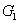
and
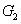
.
PC between  and
and  (
( and
and  ) can be quantified by
) can be quantified by
Equation (
22) is similar to the case of Eq. (
14). The region in which
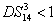
(
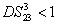
) is shown in cyan denoted as ((1, 4), (2, 3)) in Fig.
6. Therefore, beams

(
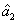
) and
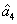
(
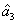
) are quantum correlated within the cyan region (
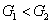
) in Fig.
6.
PC between  and
and  can be quantified by
can be quantified by
The PC with quantum correlation between the beams
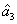
and

will be absent because
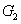
is always more than or equal to 1. This can be easily understood if one looks at the functional form of Eq. (
24). As discussed above, for this FWM + FWM + FWM network, there are three possible PCs with quantum correlation, namely
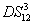
,

, and
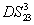
. In addition, the existence of quantum correlation between the beams
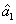
and
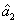
eliminates the possibility of the one between the beams
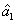
(
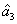
) and
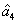
(

). In other words, beam
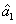
(
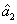
) cannot be quantum correlated with the beams
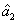
(
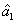
) and
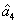
(
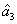
) in the same gain region. These effects in this FWM + FWM + FWM network are similar to the above mentioned repulsion effect of quantum correlation between the PCs in the FWM + FWM network.
Secondly, for the FWM+BS+BS network in Fig. 5(b), the DS of the quadruple beams is given by
In this case, the quantum correlations for the quadruple beams have remained unchanged compared with the Eq. (
4). We will analyze all the possible PCs.
PC between  and
and  can be quantified by
can be quantified by
Equation (
26) will be reduced to 1, 1/(2
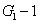
), and 1 when we set
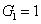
,

, and
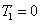
respectively, corresponding to the cases of Eq. (
8), Eq. (
4), and Eq. (
8) respectively. We can understand these physical phenomena as follows. When we set
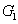
=1, the PC between the thermal states
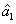
and
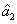
translates into the one between the vacuum state
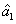
and the coherent state
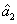
, i.e.,

. When we set
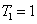
, the PC between the thermal states

and

translates into the one between the twin beams from the first FWM process, i.e.,
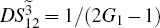
. When we set
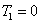
, the PC between the thermal states
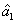
and
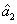
translates into the one between the vacuum state
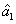
and the vacuum state
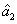
, i.e.,
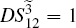
. Its value is always less than or equal to 1 for any value of

and
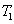
. The region in which
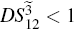
, i.e., there exists quantum correlation between the beams
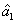
and
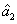
, is shown in Fig.
7(a). Figure
7(a) means the larger

and larger
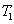
are preferred for the PC with quantum correlation between the beams
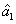
and
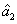
. The study of

presented above is actually the question of how to preserve or even enhance the quantum correlation between the beams
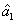
and
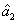
under the introduction of two lossy beamsplitters which bring the deterioration effect to the quantum correlation by the same amount of attenuation of both of the beams (
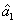
and
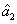
). Figure
7(a) shows that the same amount of attenuation can preserve the PC with quantum correlation between the beams
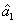
and
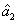
. More interestingly, in this case, the PC with quantum correlation between the beams
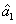
and
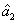
can be quantum recovered to the one between the twin beams from the first FWM process only when
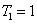
, i.e.,
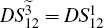
. That is to say, when

, both attenuation of the twin beams can destroy the quantum correlation between the twin beams from the first FWM process inevitably.
PC between  and
and  can be quantified by
can be quantified by
The region in which

, i.e., there exists quantum correlation between the beams
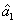
and
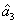
, is shown in magenta denoted as (1, 3) in Fig.
8(a). Figure
8(a) means that the PC with quantum correlation between the beams
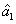
and
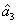
is present for the value of
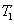
between the two boundaries
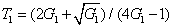
and
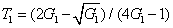
. With the increasing of
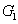
, the values of
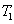
on the boundaries eventually reach the value of 1/2.
PC between  and
and  (
( and
and 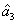 ) can be quantified by
) can be quantified by
which is similar to the case of Eq. (
18). Therefore, the beams
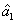
(
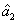
) and
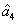
(

) are not quantum correlated to each other in this network.
PC between  and
and 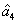 can be quantified by
can be quantified by
The region in which
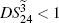
, i.e., there exists quantum correlation between the beams
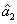
and
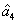
, is shown in green denoted as (2, 4) in Fig.
8(b). Figure
8(b) means that the PC with quantum correlation between the beams

and
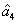
is present for the value of
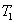
between the two boundaries
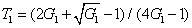
and

. With the increasing of

, the values of
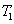
on the boundaries eventually reach the value of 1/2. As shown in Fig.
8, the sum of the boundary value of
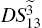
, i.e.,

(
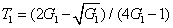
), and the boundary value of
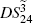
, i.e.,
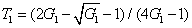
(
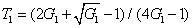
), is always equal to 1 due to the limitation of the lossy beamsplitter.
PC between  and
and  can be quantified by
can be quantified by
which is always less than or equal to 1 for any value of
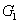
and
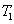
. The region in which
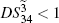
, i.e., there exists quantum correlation between the beams
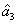
and
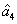
, is shown in Fig.
7(b). Figure
7(b) means that the larger
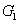
and smaller
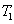
are preferred for the PC with quantum correlation between
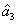
and
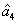
.
As Section 4 mentioned, both the FWM + FWM + FWM and FWM+BS+BS networks can preserve the quantum correlation between  and
and  under the condition of
under the condition of  and
and  , respectively. The repulsion effect between the PCs with quantum correlation is also predicted in the FWM + FWM + FWM network instead of the FWM+BS+BS network.
, respectively. The repulsion effect between the PCs with quantum correlation is also predicted in the FWM + FWM + FWM network instead of the FWM+BS+BS network.
5. ConclusionIn summary, we theoretically characterize the performances of the PCs in different quantum networks consisting of FWMs and BSs. The quantum correlation recovery and enhancement are present in the FWM+BS network and the repulsion effect phenomena between the PCs with quantum correlation are predicted in the FWM + FWM and FWM + FWM + FWM networks. Our results presented here pave the way for the manipulation of the quantum correlation in quantum networks.