The interesting coherent interaction of atoms with laser fields in three-level Λ configurations has attracted increasing attention in the studies of nonlinear and quantum optics and spectroscopy recently. Electromagnetically induced transparency (EIT) is a quantum coherence effect which has a number of important applications such as laser cooling,^[1] lasing without inversion,^[2] information storage,^[3] and magnetometry.^[4]

EIT resonance line-shape and line-width are of interest for many EIT applications. A narrow and high contrast EIT resonance is useful in many fields, especially for spectroscopy^[5,6] and precision metrology.^[7,8] In a three-level Λ scheme, the line-width caused by the nonlinear effects in EIT is governed by the relaxation rate of the ground state coherence, which is predominantly determined by the interaction time of the atom with the applied laser fields, i.e, the average time-of-flight of the atom through the laser beam.^[9,10] To obtain a narrower EIT resonance, a buffer gas can be added to the atomic vapor to prolong the interaction time.^[9,11] The addition of the buffer gas slows the diffusion of the coherently prepared atoms through the laser beam by simultaneously preserving the ground state coherence as a result of the collisions over millions of buffer gas.^[12] The line-width can be reduced by several orders of magnitude.^[13–15]

The line-shape of the EIT resonance is also affected by the thermal motion of the atoms in a vapor cell filled with a mixture of alkali atoms and inert gas at several Torr.^[16–20] For example, Sarkisyan studied the effect of different pressure of buffer gas on the EIT resonances,^[16] while Eugeniy et al. studied the influence of the laser detuning on the line shape of the EIT and observed that in the presence of a buffer gas, an absorption resonance appears, that is different from the Lorentzian shape of the usual EIT resonance.^[17,21]

What is more, compared to the case without buffer gas, the velocity selective optical pump (VSOP) effects will disappear when the vapor cell is filled with a buffer gas; this is due to the pumping process being overridden by velocity-changing. Therefore, the EIT resonance will grow up on a broadened Gaussian background, which simplifies the analysis of the spectra and supplies a good way for us to study the EIT splitting with a high resolution spectrum in a magnetic field.^[22]

The EIT resonance in the Λ system of the D₁ or D₂ line of Rb atoms in a magnetic field has been studied a lot both theoretically and experimentally.^[23–26] In most cases, the magnetic field is either parallel to the laser propagation direction, where both coupling and probe fields are seen as a combination of left- and right-circularly polarized ones, or orthogonal to the laser propagation direction but along the electric field of the probe laser, where only the coupling beam is seen as a combined field.^[27]

However, for the case with the magnetic field along the electric field of the coupling laser, the Zeeman-splitting in magnetic fields is rarely studied. In our work, we use a vapor cell filled with ⁸⁷Rb and 5 torr N₂ to remove the VSOP peaks in the Λ-type EIT for D₂ line at room temperature and present an experimental observation of Λ-type EIT by applying an external magnetic field along the electric field of the coupling laser. A skill of weighted least-square fit is used to remove the Doppler broadened background. The observed spectrum is well explained by our theoretical simulation.

Our experimental setup for the Λ-type EIT of ⁸⁷Rb in a magnetic field is shown in Fig. 1(a) and the relative transition energy level diagram is shown in Fig. 1(b). The arrangement of the optical elements has been described in detail in our previous work.^[28] The coupling laser frequency is locked to a saturation absorption spectroscopy (SAS) system and the probe laser is scanned across the D₂ line levels.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (color online) (a) Experimental setup for EIT spectral measurement. PBS: polarizing beam splitter; PM: permanent magnet; PD: photo detector. (b) Magnetic sublevels diagram of 87Rb atoms in the presence of the magnetic field. All possible polarization combinations for the Λ-EIT scheme are shown.

The polarizations of the coupling and probe lasers are linear and mutually orthogonal. The beam size is around 1 mm² for each laser. The coupling and probe laser beams are carefully superimposed on one polarization beam splitter (PBS) and then adjusted to overlap almost completely throughout the cell. The spherical-shaped Rb vapor cell is made of pyrex glass and has a diameter of 2 cm. The cell is filled with pure ⁸⁷Rb and N₂ buffer gas at a pressure of 5 Torr at room temperature. There is no magnetic field shielding outside the Rb vapor cell. A long permanent magnet is placed near the cell to apply the magnetic field to the Rb atoms. The magnetic field direction is along the y axis, which is parallel to the electric field of the coupling laser, and the strength can be controlled by changing the distance between the magnet and the cell. The maximum magnitude can be up to 500 Gs. The coupling field couples the hyperfine level 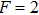of the ground state 5S_1/2 and of the excited state 5P_3/2, while the probe laser scans over the transitions from the ground state F = 1 to the excited states 5P_3/2 , and 2.

In fact, the D₂ line of the ⁸⁷Rb atoms is of multi-levels, and there will be some satellite peaks along with the EIT line due to the Doppler effect in the Λ configuration,^[29] which causes the very complicated spectrum observed. In our work, we use a pure ⁸⁷Rb vapor cell filled with N₂ buffer gas to decrease or remove this effect and only keep the EIT signal for high spectroscopy, which further helps us to study the EIT splitting in the magnetic field.

Figure 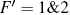2 shows the observed EIT spectra without and with N₂ buffer gas under no magnetic field. The coupling laser is locked to the transition F = 2 to , where means the cross-over peak between and 2 due to the Doppler broadening in the SAS configuration. In the case without buffer gas, we can see an EIT peak with several VSOP peaks. Obviously, the EIT signal is much narrower than that of VSOP. If we fill the cell with 5 Torr N₂, all the VSOP peaks will become much broader and their magnitudes also decrease greatly. This feature lets the EIT peak emerge on a very broadened background, and therefore the effects of VSOP will not affect our observation of the spectral change of the atom in an external field in the ground state.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (color online) The experimental observation of the EIT spectra without and with buffer gas. The coupling laser is locked to the crossover between and 2.

To remove the Doppler broadened background, we develop a numerical skill based on the least-square fit. The main idea is to set the weights of the data points around the EIT peaks to zero and a fit of the data gives a Gaussian background which we can remove from the experimental data by a subtraction. Figures 3(a) and 3(b) show the experimental spectra without and with the magnetic field and their numerical processes, where we can see that the Doppler broadening is removed completely. In Fig. 3(b), the magnetic field is B = 44.3 Gs and along the y axis, and the EIT spectral line splits into four peaks.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (color online) Experimental spectra of Rb atom with buffer gas and the removing of the broadened background: (a) B = 0, (b) B = 44.3 Gs. In both cases, we can get a good signal-to-noise ratio, thus providing a technique to study the spectrum of high resolution.

As observed in many previous works,^[17,30–32] the EIT spectral line-shape becomes asymmetric when the coupling laser is detuned far away from the resonance, which is reinvestigated in our experiment as shown in Fig. 4. The detuning of the coupling laser varying from −78.5 MHz to 346 MHz causes the EIT resonance shifting within the absorption profile of the probe laser and the line-shape of the detuned EIT resonance becomes asymmetric and non-Lorentzian. In addition, an increasing detuning of the coupling frequency leads to a significant reduction of the amplitude of the EIT peaks,^[25] even inducing a dispersive line shape. For example, when the coupling field frequency is detuned to 346 MHz, an obvious dispersion-like resonant absorption peak appears. Our simulation considering the detuning coincides well with the experimental spectrum. If we apply a magnetic field to the atom, the hyperfine energy levels will split and the coupling laser detunes away from the resonant energies as well. It also causes the EIT spectral lines to have an asymmetric structure as shown in Fig. 3(b).

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (color online) The effect of detuning of the coupling laser on the EIT spectral line with B = 0. A large detuning distorts the EIT spectral line seriously.

Unlike the case of the atom in zero magnetic field, the degeneracy of the hyperfine levels is destroyed due to the Zeeman effect, forming 13 nondegenerate magnetic sublevels as shown in Fig. 1(b). Specifically, for the case with the magnetic field parallel to the electric field of the coupling laser along y-axis, we can simplify the complex transitions by decomposition. The coupling process corresponds to a π transition, while the probe beam has a σ one that can be decomposed to be the combination of and transitions with the same weight. All possible transitions can form six Λ-type subsystems. The two sub-EIT peaks in the outside each contain one single subsystem, corresponding to the transitions from via to and via to , respectively. The two sub-EIT peaks in the middle both contain two subsystems.

Figure 5 shows the spectrum of ⁸⁷Rb in a magnetic field along the y-axis. The magnetic field varies from B = 16 Gs to B = 98 Gs. Firstly, we can see that the four EIT peaks are linearly shifted away with the magnetic field increasing. Secondly, in the low magnetic field (B = 16 Gs), the amplitudes of the middle two peaks are smaller than those of the two peaks outside. An interesting phenomenon is that with the magnetic field increasing, the amplitudes of the two middle peaks become larger and larger than the ones outside. They do not keep a constant ratio at all as expected.

Fig. 5.

	Figure Option ViewDownloadNew Window
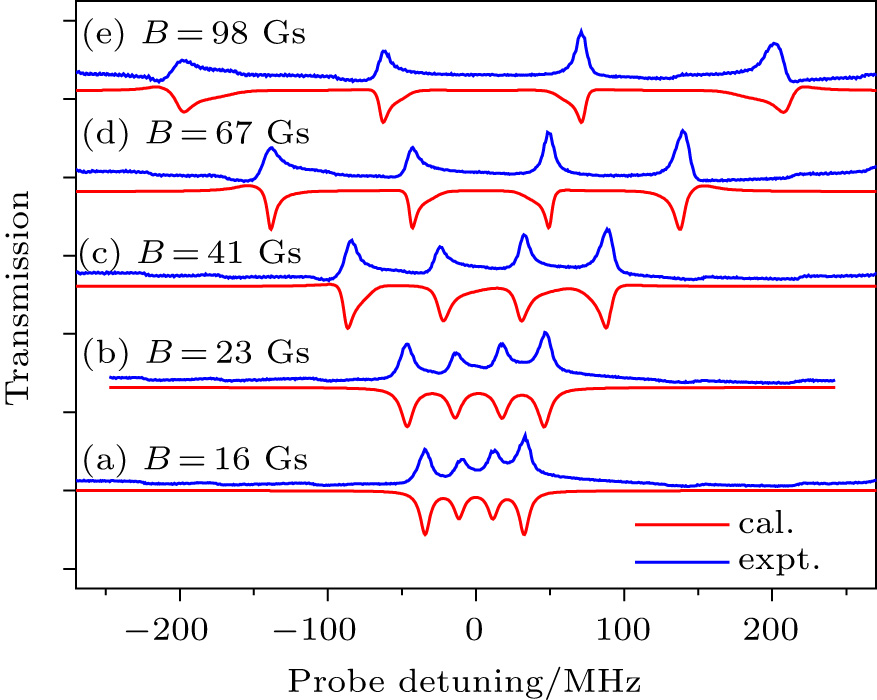	Fig. 5. (color online) The observed and calculated splittings of EIT resonances in magnetic fields along the coupling laser polarization direction at different magnetic field intensities.

Usually the spectral line intensity is determined directly by the transition probability between different Zeeman sublevels, in our case, from F = 2 to 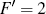. For example, the transition probabilities from to (corresponding to the two outside peaks) are twice as large as those of the transitions to (corresponding to the two inside peaks).^[33] It agrees with the observation at the low magnetic field, i.e., at B = 16 Gs.

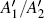
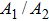
However, as discussed previously, the magnitude of the resonance is also dependent on the detuning of the coupling laser frequency from the corresponding atomic transition. To show the influence of the detuning caused by the magnetic field on the magnitude of the EIT resonance, we further compare the results with and without considering the detuning in our calculation, which is shown in Fig. 6. The blue and red lines indicate the calculated results with and without considering the detuning, respectively. In the low magnetic field as shown in Fig. 6(a), the simulated spectral line intensity ratio having considered the detuning is almost the same as the ratio of the transition intensity, which indicates that in the low magnetic field, the amplitudes of the EIT peaks are mainly determined by the transition intensities between different sub-levels and we can ignore the influence of the detuning on the amplitudes.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. (color online) The calculated results with and without considering the detuning of the coupling laser at two different magnetic field intensities: (a) B = 16 Gs and (b) B = 67 Gs. The blue lines are the simulated spectra considering the detuning, while the red lines are the calculated transition intensities.

However, the detuning plays a more and more important role for the line intensity and position when the magnetic field increases, as shown in Fig. 6(b). We can see that the amplitude ratio considering the detuning decreases to 1 from its original ratio . This is because the outside EIT peaks possess a much larger red- or blue-detuning, which distorts the resonant line shape and reduces the amplitudes of their spectral line intensities significantly.^[30] For example, at the magnetic field of B = 98 Gs shown in Fig. 5(e), the detunings of the coupling laser for the two outside peaks can reach more than 200 MHz, resulting in a remarkable reduction of the spectral amplitudes. In addition, the simulated spectral line position also shifts a little. It also indicates that we have to choose a zero detuning line if this Doppler free technique is used for a laser frequency locking.

We have obtained a high resolution of EIT splittings in a Rb vapor cell with N₂ buffer gas in a magnetic field at room temperature. With the additional 5 Torr N₂, the VSOP peaks due to optical pumping almost disappear and only the EIT signals are kept in the spectra due to the collision effects by the buffer gas. We present a method by a least-square fit to remove the Doppler broadening completely which keeps only the EIT peaks. These two techniques simplify the analysis of the observed EIT spectral splittings in the magnetic field. The dependence of the splitting line shape and intervals of sub-EIT windows on the magnetic field have been investigated. When the applied magnetic field is along the polarization direction of the coupling laser, the EIT peak splits into four sub-ones. An asymmetric spectral line shape can be observed for the deep detunings caused by the Zeeman level splitting. All experimental observations are well explained by a simulation considering the detuning effect. Our work provides a method to lock the laser to a given frequency by tuning the magnetic field.