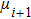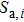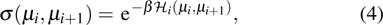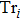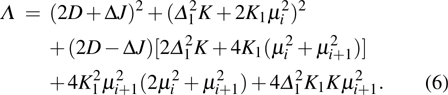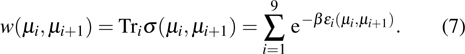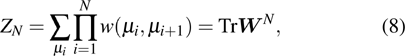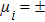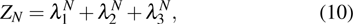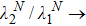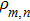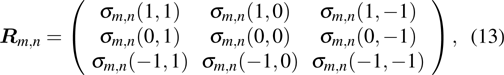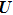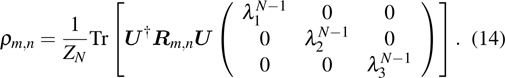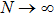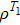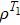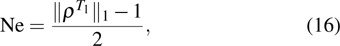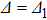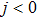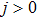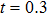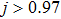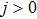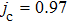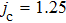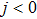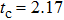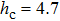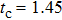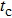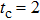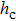Thermal entanglement of the spin-1 Ising–Heisenberg diamond chain with biquadratic interaction
Department of Physics, Hubei University, Wuhan 430062, China
† Corresponding author. E-mail:
maozhu1115@163.com binzhou@hubu.edu.cn
1. IntroductionQuantum entanglement is one of the most significant characteristics of a quantum system, and it is regarded as a crucial resource of quantum communication and quantum information.[1–4] People have widely studied the entanglement of solid state systems, such as Heisenberg spin system, which may be used as gate operations in solid state quantum computation processors.[5,6] The thermal fluctuation can destroy quantum states, thus it is essential to emphasize the role of temperature in the study of the entanglement. The concept of thermal entanglement has been proposed in the preparation of entangled states,[7,8] in which the effects of temperature are viewed as the external control. It is noted that the thermal entanglement in Heisenberg spin systems has attracted considerable attention in theoretical studies.[9–14]
Recently, low-dimensional magnetic materials possessing novel quantum magnetic phenomena became the new favorite for the researchers. The diamond Heisenberg spin chain is one of them. Takano et al. first studied theoretically the ground state of an ideal diamond spin chain in 1996, and they found that the phase transitions would take place in the system when the ratio between the exchange parameters varies.[15] In particular, Kikuchi et al. verified that the natural mineral azurite  can be regarded as an actual material for the frustrated diamond chain model.[16] Later on, the 1/3 magnetization plateau in the diamond-chain compound
can be regarded as an actual material for the frustrated diamond chain model.[16] Later on, the 1/3 magnetization plateau in the diamond-chain compound  was observed in the experiment.[17] Since then, the magnetic properties of the azurite were intensively studied.[18–22] The Heisenberg spin diamond chain is a kind of important and interesting model. However, the rigorous theoretical treatment of quantum Heisenberg diamond chains is a very difficult task due to a non-commutability of spin operators involved in these models. Therefore, a novel class of the simplified versions named the geometrically frustrated Ising–Heisenberg diamond chain was introduced.[23–25] Various physics properties of spin-1/2 Ising–Heisenberg diamond chain have been extensively investigated.[26–31] For instance, the thermal entanglement of the Ising–Heisenberg diamond chain with Dzyaloshinskii–Moriya interaction was investigated in Ref. [30]. Meanwhile, it is noted that the mixed spin Ising–Heisenberg diamond chain has also attracted much attention.[24,32–35] The entanglement, magnetic, and quadrupole moment properties of the mixed spin Ising–Heisenberg diamond chain have been discussed in Ref. [35].
was observed in the experiment.[17] Since then, the magnetic properties of the azurite were intensively studied.[18–22] The Heisenberg spin diamond chain is a kind of important and interesting model. However, the rigorous theoretical treatment of quantum Heisenberg diamond chains is a very difficult task due to a non-commutability of spin operators involved in these models. Therefore, a novel class of the simplified versions named the geometrically frustrated Ising–Heisenberg diamond chain was introduced.[23–25] Various physics properties of spin-1/2 Ising–Heisenberg diamond chain have been extensively investigated.[26–31] For instance, the thermal entanglement of the Ising–Heisenberg diamond chain with Dzyaloshinskii–Moriya interaction was investigated in Ref. [30]. Meanwhile, it is noted that the mixed spin Ising–Heisenberg diamond chain has also attracted much attention.[24,32–35] The entanglement, magnetic, and quadrupole moment properties of the mixed spin Ising–Heisenberg diamond chain have been discussed in Ref. [35].
According to the experimental results, the magnetic properties of magnetic complex  and molecular compound
and molecular compound  can be described by the spin-1 Ising–Heisenberg diamond chain model.[36,37] Meanwhile, it has been verified that the ground states and magnetization curves of the spin-1 Ising–Heisenberg diamond chain have more diversity than the case of spin-1/2.[38,39] Hovhannisyan et al. rigorously solved the spin-1 Ising–Heisenberg diamond chain with the second-neighbor interaction between nodal spins.[40] In order to further understand the nature of the quantum phase transition, the thermal entanglement of the spin-1 Ising–Heisenberg diamond chain was investigated in Ref. [38]. Very recently, the partition function zeros and magnetization plateaus of the spin-1 Ising–Heisenberg diamond chain with the biquadratic interaction term were also studied.[41] It was found that the spin-1 Ising–Heisenberg diamond chain model possesses a large variety of ground-state phases due to the presence of biquadratic and single-ion anisotropy parameters.[41] Note that the effect of the biquadratic interaction on the thermal entanglement was not considered in the previous work.[38] Thus, in this paper we will investigate the thermal entanglement of the spin-1 Ising–Heisenberg diamond chain when the biquadratic interaction is considered, and the negativity will be calculated as the measurement of the thermal entanglement by means of the transfer-matrix approach.[42]
can be described by the spin-1 Ising–Heisenberg diamond chain model.[36,37] Meanwhile, it has been verified that the ground states and magnetization curves of the spin-1 Ising–Heisenberg diamond chain have more diversity than the case of spin-1/2.[38,39] Hovhannisyan et al. rigorously solved the spin-1 Ising–Heisenberg diamond chain with the second-neighbor interaction between nodal spins.[40] In order to further understand the nature of the quantum phase transition, the thermal entanglement of the spin-1 Ising–Heisenberg diamond chain was investigated in Ref. [38]. Very recently, the partition function zeros and magnetization plateaus of the spin-1 Ising–Heisenberg diamond chain with the biquadratic interaction term were also studied.[41] It was found that the spin-1 Ising–Heisenberg diamond chain model possesses a large variety of ground-state phases due to the presence of biquadratic and single-ion anisotropy parameters.[41] Note that the effect of the biquadratic interaction on the thermal entanglement was not considered in the previous work.[38] Thus, in this paper we will investigate the thermal entanglement of the spin-1 Ising–Heisenberg diamond chain when the biquadratic interaction is considered, and the negativity will be calculated as the measurement of the thermal entanglement by means of the transfer-matrix approach.[42]
It is noted that synthesizing Ising–Heisenberg chains has recently attracted special attention, and the Ising–Heisenberg chains play an important role in providing evidence for several novel quantum states. The study of entanglement properties of the Ising–Heisenberg chains should provide a new perspective for understanding a relationship between the entanglement of a many-body system and the existence of the quantum phase transitions, and also has potential application in the proposals for quantum chips based on solid state materials. In the Ising–Heisenberg diamond chain, the Ising spins locate at the nodal sites and the Heisenberg spin dimers are on the interstitial decorating sites of the diamond chain. The nodal Ising spins represent a barrier for quantum fluctuations, and each Heisenberg dimer interacts with its neighboring dimer through the classical Ising-type exchange interaction. It is found that the states of two adjacent dimers become disentangled and the only entangled pair in the Ising–Heisenberg diamond chain is the Heisenberg dimer.[26] Thus, in this paper, we focus on the thermal entanglement between two Heisenberg-type spins in the Heisenberg dimer. The Ising–Heisenberg diamond chain can be solved exactly through a transfer-matrix approach to obtain a partition function on a whole diamond chain. With the aim of studying the entanglement of the Heisenberg dimer, we will perform the reduced density operator bounded by Ising spins along a diamond chain, and trace out over all Heisenberg spins and Ising spins except the Heisenberg dimer considered. Although Ising coupling does not contribute directly in quantum entanglement, the remaining diamond blocks’ coupling contributions to the entanglement of the Heisenberg dimer are attributed to the reduced density matrix of the Heisenberg dimer.
2. Model and methodWe consider the spin-1 Ising–Heisenberg diamond chain model with the biquadratic interaction in the presence of an external magnetic field. The block of the diamond chain consists of two mixed nodal Ising spins (μi, 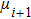 ) and the interstitial decorating Heisenberg spin dimers (
) and the interstitial decorating Heisenberg spin dimers (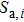 ,
,  ). The illustration of this model is shown in Fig. 1, and the system considered is described by the following Hamiltonian:[41]
). The illustration of this model is shown in Fig. 1, and the system considered is described by the following Hamiltonian:[41]
where
Here,  (
( ) are the Heisenberg spin-1 operators, and
) are the Heisenberg spin-1 operators, and  is z projection of Ising spin-1 operator. J is the Heisenberg interaction term, and J1 is the interaction parameter between the nearest-neighboring Ising and Heisenberg spins. K is the biquadratic Heisenberg interaction term parameter, and K1 is the analogue of a biquadratic Ising interaction term.
is z projection of Ising spin-1 operator. J is the Heisenberg interaction term, and J1 is the interaction parameter between the nearest-neighboring Ising and Heisenberg spins. K is the biquadratic Heisenberg interaction term parameter, and K1 is the analogue of a biquadratic Ising interaction term.  and
and  stand for anisotropy parameters, D and D1 represent the single-ion anisotropy parameters of Heisenberg and Ising spins. The last two terms in Eq. (2) are contributions of an external magnetic field interacting with the Heisenberg and Ising spins. In the following, we will apply the periodic boundary condition (
stand for anisotropy parameters, D and D1 represent the single-ion anisotropy parameters of Heisenberg and Ising spins. The last two terms in Eq. (2) are contributions of an external magnetic field interacting with the Heisenberg and Ising spins. In the following, we will apply the periodic boundary condition ( ) for convenience.
) for convenience.
We are going to gain the partition function of the whole diamond chain by means of transfer-matrix approach.[27,38,43] It is necessary to confirm the commutation relation  for
for 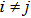 , which ensures the blocks of diamond chain are separable, and allows us to partially factorize the partition function of the model and represent it as[38]
, which ensures the blocks of diamond chain are separable, and allows us to partially factorize the partition function of the model and represent it as[38]
with
where

,

is Boltzmann’s constant, and
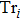
means a trace over the states of two Heisenberg spins from the
i-th block.

means a summation over spin states of all Ising spins. Hereafter the Boltzmann’s constant is set to unity

for simplicity. After diagonalizing the block Hamiltonian

, we obtain the following eigenvalues depending on the Ising spins:
where
According to the above eigenvalues and tracing out over the operator σ, one can get the Boltzmann factor w:[27]
Using the transfer-matrix notation and periodic boundary condition, equation (3) can be rewritten as[39]
where

can be viewed as a 3 × 3 transfer matrix
where indices ±1 and 0 denote
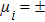
1, 0 for classical Ising spins. Thus, the partition function of the spin-1 Ising–Heisenberg diamond chain can be expressed through three eigenvalues of the transfer matrix (
9)
[41,43]
where
λ1,
λ2,
λ3 are the three transfer-matrix eigenvalues in descending order. Considering the thermodynamic limit

, the specific values
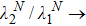
0 and

0, so that we can completely ignore the contribution of two smaller transfer-matrix eigenvalues to the partition function. Then, equation (
10) becomes
Now we are interested in the negativity as the measurement of the thermal entanglement. For completing our further calculation, it is essential to obtain the reduced density matrix ρ, which is obtained by tracing over all Heisenberg spins and Ising spins except for Heisenberg spins at the interesting block. Using the transfer-matrix approach, the elements of reduced density matrix 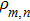 can be expressed as follows:[27]
can be expressed as follows:[27]
with
where
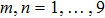
. Now we assume that {
v1,
v2,
v3} is the complete set of vectors corresponding to eigenvalues
λ1,
λ2,
λ3. We denote by the matrix
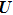
having
vi vectors as columns, and then equation (
12) can be expressed as
[38]
Considering the thermodynamic limit 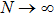 , the reduced density operator elements
, the reduced density operator elements  become
become
If we define the Heisenberg spins in an orthonormal but otherwise arbitrary bipartite product basis like  , where indices a and b denote a or b Heisenberg spins respectively. The bipartite density matrix which transposes to the first subsystem
, where indices a and b denote a or b Heisenberg spins respectively. The bipartite density matrix which transposes to the first subsystem 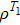 will get from the following way:
will get from the following way:  . Vidal and Werner have defined the negativity as the sum of negative eigenvalues εi of bipartite density matrix
. Vidal and Werner have defined the negativity as the sum of negative eigenvalues εi of bipartite density matrix 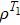 :
:  .[42] The bipartite density matrix is partially transposed with respect to the first subsystem in the definition; obviously transposing the second subsystem is equivalent to transposing the first one. Moreover, the negativity can be defined as[42]
.[42] The bipartite density matrix is partially transposed with respect to the first subsystem in the definition; obviously transposing the second subsystem is equivalent to transposing the first one. Moreover, the negativity can be defined as[42]
where

is the trace norm of

, also equal to the sum of the absolute values of the eigenvalues of the bipartite density matrix

.
3. Results and discussionIn this section, we find the biquadratic interaction plays an interesting role in the thermal entanglement of the spin-1 Ising–Heisenberg diamond chain. The negativity is obtained by the numerical calculation, and we assume there is no entanglement when the value of negativity is less than 0.001 in the numerical calculation. For simplicity, a uniform external magnetic field (i.e.,  ), and
), and  ,
,  ,
, 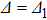 are considered in the following discussion. We use dimensionless parameters and present all parameters in units of the Ising-type interaction parameter J1, such as
are considered in the following discussion. We use dimensionless parameters and present all parameters in units of the Ising-type interaction parameter J1, such as
 | |
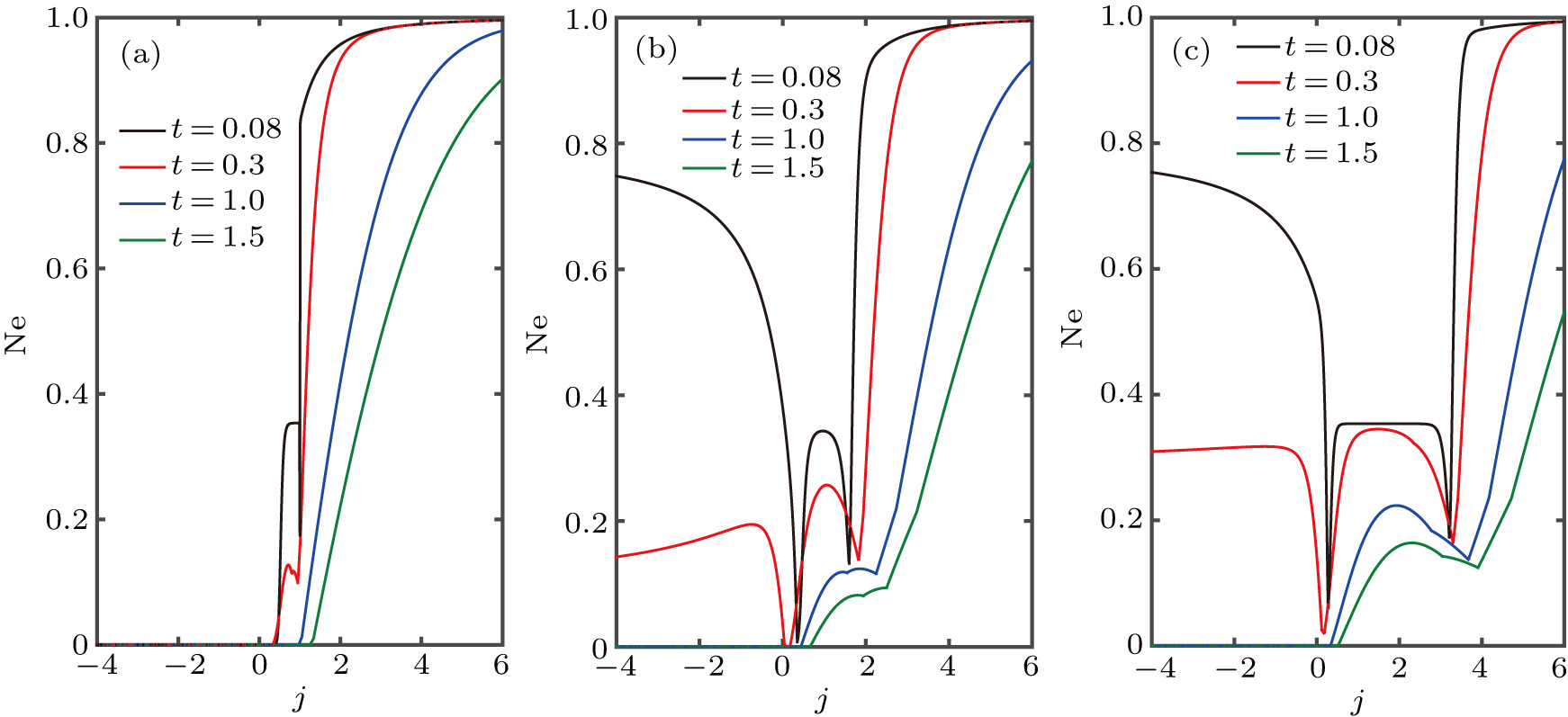
3.1. The case of Ising–XXX coupling modelNow we consider the case of the isotropic Heisenberg (Ising–XXX) coupling model (i.e., Δ = 1). Firstly we discuss the negativity of the spin-1 Ising–Heisenberg diamond chain without the external magnetic field (i.e., h = 0). In Fig. 2, the variations of negativity Ne with Heisenberg coupling parameter j for different values of temperature t are plotted in three cases of the biquadratic interaction parameter k. In Fig. 2(a), the biquadratic interaction is absent (i.e., k = 0), and it is shown that entanglement does not occur when 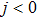 (corresponding to the case of ferromagnetic coupling). However, the case of antiferromagnetic coupling (i.e.,
(corresponding to the case of ferromagnetic coupling). However, the case of antiferromagnetic coupling (i.e., 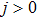 ) is contrary to the case of ferromagnetic coupling. With the increase in j, the system experiences from unentanglement to entanglement. Furthermore, the higher the temperature of the system is, the greater the Heisenberg coupling parameter j is required to induce entanglement. For instance, there is entanglement in the system when
) is contrary to the case of ferromagnetic coupling. With the increase in j, the system experiences from unentanglement to entanglement. Furthermore, the higher the temperature of the system is, the greater the Heisenberg coupling parameter j is required to induce entanglement. For instance, there is entanglement in the system when  at
at 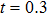 , while the system gets entangled when
, while the system gets entangled when 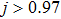 at t = 1.0. At near-zero temperature (e.g., t = 0.08), a plateau (
at t = 1.0. At near-zero temperature (e.g., t = 0.08), a plateau ( , Ne = 0.3535) appears before getting the maximal entanglement, while this plateau generally disappears with increasing temperature. Figures 2(b) and 2(c) show the case with the biquadratic interaction k = 0.5 and 1.0, respectively. It is interesting to observe that due to the biquadratic interaction the entanglement also occurs in the region of ferromagnetic coupling at low temperature (e.g., the cases with t = 0.08 and t = 0.3 in Figs. 2(b) and 2(c)). For the case with k = 1.0 at t = 0.08 in Fig. 2(c), in the region of ferromagnetic coupling (i.e.,
, Ne = 0.3535) appears before getting the maximal entanglement, while this plateau generally disappears with increasing temperature. Figures 2(b) and 2(c) show the case with the biquadratic interaction k = 0.5 and 1.0, respectively. It is interesting to observe that due to the biquadratic interaction the entanglement also occurs in the region of ferromagnetic coupling at low temperature (e.g., the cases with t = 0.08 and t = 0.3 in Figs. 2(b) and 2(c)). For the case with k = 1.0 at t = 0.08 in Fig. 2(c), in the region of ferromagnetic coupling (i.e.,  ) the negativity generally decreases with
) the negativity generally decreases with  decreasing. Meanwhile, in the region of antiferromagnetic coupling (i.e.,
decreasing. Meanwhile, in the region of antiferromagnetic coupling (i.e., 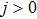 ) the variation of negativity Ne with Heisenberg coupling parameter j shows a nonmonotonic behavior, and there are two dips in the curve of the variation of negativity. Moreover, a wide plateau between two dips is observed. However, with the increase in temperature, the negativity of the region of ferromagnetic coupling vanishes (e.g., the cases with t = 1.0 and t = 1.5 in Figs. 2(b) and 2(c)). At t = 1.0 and t = 1.5, due to the existence of the biquadratic interactions, in the region of antiferromagnetic coupling the threshold Heisenberg coupling parameter
) the variation of negativity Ne with Heisenberg coupling parameter j shows a nonmonotonic behavior, and there are two dips in the curve of the variation of negativity. Moreover, a wide plateau between two dips is observed. However, with the increase in temperature, the negativity of the region of ferromagnetic coupling vanishes (e.g., the cases with t = 1.0 and t = 1.5 in Figs. 2(b) and 2(c)). At t = 1.0 and t = 1.5, due to the existence of the biquadratic interactions, in the region of antiferromagnetic coupling the threshold Heisenberg coupling parameter  (the minimal value of j required to induce entanglement) decreases. For instance, at t = 1.0, corresponding to the parameter k = 0, 0.5, and 1.0,
(the minimal value of j required to induce entanglement) decreases. For instance, at t = 1.0, corresponding to the parameter k = 0, 0.5, and 1.0, 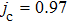 , 0.44, and 0.33, respectively; at t = 1.5, the corresponding
, 0.44, and 0.33, respectively; at t = 1.5, the corresponding 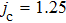 , 0.66, and 0.51.
, 0.66, and 0.51.
Next we study the role of external magnetic field h on the same system. In Fig. 3, the variations of negativity Ne with Heisenberg coupling parameter j for different values of temperature t are plotted in three cases of the external magnetic field parameter h, where we choose k = 1. It is observed that the external magnetic field suppresses the occurrence of the entanglement induced by the biquadratic interaction in the region of ferromagnetic coupling (e.g., the cases with t = 0.08 and t = 0.3). Especially, for the case of external magnetic field parameter h = 2.0, the entanglement vanishes in the region of ferromagnetic coupling (i.e., 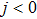 ) shown in Fig. 3(c). In the region of antiferromagnetic coupling, at low temperature (e.g., t = 0.08) the plateau in the curve of the variation of negativity with j becomes wider when the external magnetic field increases. Moreover, for small antiferromagnetic coupling parameter, the negativity increases with the parameter h increasing (e.g., the cases with t = 1.0 and t = 1.5 in Fig. 3).
) shown in Fig. 3(c). In the region of antiferromagnetic coupling, at low temperature (e.g., t = 0.08) the plateau in the curve of the variation of negativity with j becomes wider when the external magnetic field increases. Moreover, for small antiferromagnetic coupling parameter, the negativity increases with the parameter h increasing (e.g., the cases with t = 1.0 and t = 1.5 in Fig. 3).
In general, temperature suppresses the occurrence of the entanglement, and the entanglement will disappear when temperature is beyond certain threshold temperature  . In Fig. 4, we plot the dependence of the threshold temperature
. In Fig. 4, we plot the dependence of the threshold temperature  on the external magnetic field parameter h for different values of the biquadratic interaction parameter k with the Heisenberg coupling parameter j = 1. The areas surrounded by the curves and the coordinate axis represent the occurrence of entanglement. In absence of the external magnetic field (i.e., h = 0), the maximum threshold temperature increases with the parameter k increasing. For instance, the threshold temperature
on the external magnetic field parameter h for different values of the biquadratic interaction parameter k with the Heisenberg coupling parameter j = 1. The areas surrounded by the curves and the coordinate axis represent the occurrence of entanglement. In absence of the external magnetic field (i.e., h = 0), the maximum threshold temperature increases with the parameter k increasing. For instance, the threshold temperature  when k = 0, while for k = 0.5 and 1.0,
when k = 0, while for k = 0.5 and 1.0, 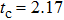 and 2.65, respectively. It is found that the variation of the maximum magnitude of threshold magnetic field with k are nonmonotonic. For instance, when k = 0, the maximum threshold magnetic field
and 2.65, respectively. It is found that the variation of the maximum magnitude of threshold magnetic field with k are nonmonotonic. For instance, when k = 0, the maximum threshold magnetic field  , but when k = 0.5 and 1.0,
, but when k = 0.5 and 1.0,  and 6.16, respectively. It is also shown that there exists the phenomenon of entanglement revival. Taking the case of k = 1 into account, for the magnetic field
and 6.16, respectively. It is also shown that there exists the phenomenon of entanglement revival. Taking the case of k = 1 into account, for the magnetic field 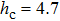 , there is no entanglement when the temperature
, there is no entanglement when the temperature  , but the entanglement will occur once the temperature exceeds 0.61, and it will maintain until
, but the entanglement will occur once the temperature exceeds 0.61, and it will maintain until 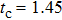 . When the temperature is higher than 1.45, the entanglement will disappear again.
. When the temperature is higher than 1.45, the entanglement will disappear again.
3.2. The case of Ising–XXZ coupling modelNow, we proceed to discuss the case of anisotropic Heisenberg (Ising–XXZ) coupling model. First we consider the case without external magnetic field (i.e., h = 0). In the region of antiferromagnetic coupling (e.g., j = 1), the variations of negativity Ne with temperature parameter t for different values of the anisotropy parameter Δ are plotted in Fig. 5, where two cases of the biquadratic interaction parameter k, i.e., k = 0 and k = 1, are investigated respectively. From Fig. 5, it is shown that the entanglement will disappear as the temperature reaches certain threshold temperature (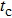 ), and including the biquadratic interaction leads to the increase in the threshold temperature
), and including the biquadratic interaction leads to the increase in the threshold temperature  . On the other hand, it is found that in the absence of the biquadratic interaction (i.e., k = 0) the anisotropy parameter Δ plays an importance role in the properties of the entanglement (see Fig. 5(a)). However, due to the biquadratic interaction the effect of the anisotropy parameter Δ will be suppressed at near zero temperature (see Fig. 5(b)). In particular, in the case of biquadratic interaction k = 1, for different anisotropy parameters Δ the maximum values of the negativity are the same (Ne = 0.3535, shown in Fig. 5(b)).
. On the other hand, it is found that in the absence of the biquadratic interaction (i.e., k = 0) the anisotropy parameter Δ plays an importance role in the properties of the entanglement (see Fig. 5(a)). However, due to the biquadratic interaction the effect of the anisotropy parameter Δ will be suppressed at near zero temperature (see Fig. 5(b)). In particular, in the case of biquadratic interaction k = 1, for different anisotropy parameters Δ the maximum values of the negativity are the same (Ne = 0.3535, shown in Fig. 5(b)).
We illustrate the density plot of negativity depending on the anisotropy parameter Δ and temperature t in Fig. 6, where three cases with different values of external magnetic field parameter (i.e., h = 0, 1, 2) are shown respectively. The color bars show different colors represent different degrees of entanglement, e.g., deep red corresponds to the maximum entangled region, and deep blue means the unentangled region. In general, the negativity Ne will disappear at higher temperature. In the presence of the magnetic field, the variations of the entangled region are obviously observed. For instance, for the case of magnetic field parameter h = 2 (Fig. 6(c)), the negativity vanishes when the anisotropy parameter  .
.
In Fig. 7, we plot the dependence of the threshold temperature  on the external magnetic field parameter h for different values of the anisotropy parameters Δ with j = 1 and k = 1, where the area around the curve and the coordinate axis is the entangled region. The result shows that the region of entanglement will enlarge with the raising of the anisotropy parameter. For Δ = 0.5, 1, and 1.1, the maximum threshold temperatures are
on the external magnetic field parameter h for different values of the anisotropy parameters Δ with j = 1 and k = 1, where the area around the curve and the coordinate axis is the entangled region. The result shows that the region of entanglement will enlarge with the raising of the anisotropy parameter. For Δ = 0.5, 1, and 1.1, the maximum threshold temperatures are 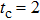 , 2.65, and 2.8, and the maximum threshold magnetic field parameters are
, 2.65, and 2.8, and the maximum threshold magnetic field parameters are  , 6.15, and 8.75, respectively. The entanglement revival phenomena are also observed in this parameter space. For instance, in the case with Δ = 1.1, taking the threshold magnetic field
, 6.15, and 8.75, respectively. The entanglement revival phenomena are also observed in this parameter space. For instance, in the case with Δ = 1.1, taking the threshold magnetic field  into account, the entanglement vanishes until the temperature increases up to 0.7, and the entanglement will occur in the region of
into account, the entanglement vanishes until the temperature increases up to 0.7, and the entanglement will occur in the region of  , but disappears again when the temperature is higher than 1.5.
, but disappears again when the temperature is higher than 1.5.
4. ConclusionIn this paper, we investigate the thermal entanglement of spin-1 Ising–Heisenberg diamond chain with biquadratic interaction. The negativity is chosen as the measurement of the thermal entanglement, and is calculated by means of the transfer-matrix approach. Firstly, we study the property of thermal entanglement in the Ising–XXX coupling model. It is found that in the case without the biquadratic interaction entanglement can occur in the region of antiferromagnetic coupling, while in the region of ferromagnetic coupling the entanglement disappears. Due to including of the biquadratic interaction, the entanglement also occurs in the region of ferromagnetic coupling at low temperature. On the other hand, if the external magnetic field is applied, it is shown that the external magnetic field will suppress the occurrence of the entanglement induced by the biquadratic interaction in the region of ferromagnetic coupling. Meanwhile, for small antiferromagnetic coupling parameter, the negativity increases with the external magnetic field increasing. Next, we consider the Ising–XXZ coupling model. In the region of antiferromagnetic coupling, due to the biquadratic interaction, the effect of the anisotropy parameter on the entanglement will be suppressed at near zero temperature. Moreover, the biquadratic interaction also leads to increase in the threshold temperature. Additionally, it is observed that there are the entanglement revival phenomena in both models considered. Although entanglement should not manifest itself in macroscopic objects due to the influence of the surroundings that induce the decoherence phenomena, some experiments of low-dimensional spin systems have confirmed that the entangled state can exist in solid state materials at finite temperature.[44,45] To a certain extent, our theoretical analysis of the spin-1 Ising–Heisenberg diamond chain will provide better understanding of the thermal entanglement of homometallic magnetic complex  . Since many proposals for quantum chips are based on solid materials, the entanglement of Heisenberg spin particles studied in the paper is of a great relevance to and has potential application in the area of quantum information and quantum computation based on solid state materials.
. Since many proposals for quantum chips are based on solid materials, the entanglement of Heisenberg spin particles studied in the paper is of a great relevance to and has potential application in the area of quantum information and quantum computation based on solid state materials.