† Corresponding author. E-mail:
This paper investigates the cooperative formation problem via impulsive control for a class of networked Euler–Lagrange systems. To reduce the energy consumption and communication frequency, the impulsive control method and cooperative formation control approach are combined. With the consideration of system uncertainties and communication delays among agents, neural networks-based adaptive technique is used for the controller design. Firstly, under the constraint that each agent interacts with its neighbors only at some sampling moments, an adaptive neural-networks impulsive formation control algorithm is proposed for the networked uncertain Euler–Lagrange systems without communication delays. Using Lyapunov stability theory and Laplacian potential function in the graph theory, we conclude that the formation can be achieved by properly choosing the constant control gains. Further, when considering communication delays, a modified impulsive formation control algorithm is proposed, in which the extended Halanay differential inequality is used to analyze the stability of the impulsive delayed dynamical systems. Finally, numerical examples and performance comparisons with continuous algorithm are provided to illustrate the effectiveness of the proposed methods.
With the development of the research community of system control, cooperative control of multi-agent systems (MAS) has gained increasing attention for the advantages of completing more complex assignments and increasing system reliabilities.[1] With these advantages, cooperative control of MAS has been used in many fields, such as the consensus of wireless networks,[2] synchronization of robots,[3] and formation of spacecrafts.[4] Thus, the cooperative control of MAS is a significant research issue.
One of the basic research problems in cooperative control of MAS is the distributed consensus problem, in which the distributed consensus control law is designed for each agent such that all the agents converge to a common state.[5] To solve the distributed consensus problem, an average-consensus control algorithm was investigated in Ref. [6] for the first-order linear systems under a connected undirected graph. The authors in Ref. [7] extended the results in Ref. [6] to the double integrator systems under a directed graph with a directed spanning tree.
Different from the distributed consensus control for the networked linear systems,[5–7] Liu et al.[8] designed a distributed consensus algorithm for the networked Euler–Lagrange systems with parametric uncertainties under a jointly connected undirected graph. The Euler–Lagrange system is a special second-order nonlinear system, which can be used to represent a large class of practical mechanical systems, such as underwater vehicles, robots, and satellites.[9] The distributed adaptive coordination for multiple Euler–Lagrange systems under a directed graph was developed in Refs. [10] and [11]. In Ref. [12], the synchronization problem of networked uncertain Euler–Lagrange systems on directed communication topologies was investigated.
For the distributed control problem of networked systems, model uncertainties, stochastic disturbances, and communication constraints are mainly considered. Unknown parameters were considered for the distributed consensus control for networked Euler–Lagrange systems in Ref. [13]. To handle the uncertainties, the authors in Ref. [14] designed a distributed consensus algorithm for the first-order systems with unknown bounded disturbances under an undirected graph. Due to the long distance between agents and the time for data-processing in each agent, communication delays always exist in practice. Considering the input and communication delays, Tian et al.[15] designed the decentralized consensus algorithms for the linear systems under undirected and directed graphs, in which the condition of system consensus is dependent on input delays but independent of communication delays. The distributed consensus problem under the undirected graph with communication delays was investigated in Ref. [16] for the networked linear systems.
Summarizing the above results, we can conclude that the consensus control algorithms proposed in Refs. [5]–[10], [12]–[16] are all continuous, which means that the energy for the control system should be provided all the time. However, the energy carried in each system is usually limited.[17,18] Besides, in the studies of Refs. [5]–[10], [12]–[16], the information interaction among agents is always required, which increases the energy consumption and communication burden.
To lower the energy consumption and communication burden in the distributed control of MAS, some researchers proposed the impulsive control for the distributed control problem. In Ref. [19], an impulsive consensus control algorithm was proposed for the networked first-order linear MAS under a directed graph. The authors in Ref. [20] extended the results in Ref. [19] to the networked second-order linear MAS. In Ref. [21], the heterogeneous communication delays among agents were further considered for the distributed consensus problem for the networked second-order linear MAS via impulsive control method. However, in the above references,[19–21] the system model is linear. Tang et al.[22] researched the leader-following impulsive consensus control problem for the networked nonlinear MAS with communication delays. In Ref. [23], the distributed impulsive consensus control algorithm was designed for the networked Euler–Lagrange systems. The authors in Ref. [24] extended the results in Ref. [23] to the case with probabilistic communication delays. However, the model parameters of the Euler–Lagrange systems need to be known for the distributed consensus controller designed in Refs. [23] and [24].
The consensus theory in multi-agent systems can be used as a powerful tool to solve the cooperative formation problem where the cooperative formation control algorithm for each agent is designed such that all agents keep relative distance or attitude. Based on the overview of the above references,[1–22] this paper studies the cooperative impulsive formation control problem for the networked Euler–Lagrange systems under a directed graph. The networked Euler–Lagrange systems are subjected to uncertain dynamics, external disturbances, and communication delays. Moreover, the information interactions of each agent with its neighbors are only at some discrete moments. The proposed cooperative formation algorithms are independent of the system model.
Compared with the previous results on cooperative continuous consensus control[5–10,12–16] and distributed impulsive consensus control,[19–24] this study mainly has three advantages.
(i) The cooperative impulsive formation control is investigated for the networked MAS. In comparison to the distributed continuous consensus control algorithm,[5–10,12,13,15,16,16] the energy consumption and the communication burden are reduced.
(ii) Each agent is modeled by nonlinear Euler–Lagrange equation, which can be used to represent a large class of practical mechanical systems. In comparison to the linear systems,[5,6,14,15] it is more challenging to design a cooperative formation control algorithm for a nonlinear Euler–Lagrange system. Furthermore, the uncertain dynamics and external disturbances are considered. Compared with Refs. [23] and [24], the proposed cooperative formation algorithms are independent on the system model.
(iii) The information interactions are more constrained. The communication delays between agents are considered, while in Refs. [5]–[10] and [12]–[14], the proposed algorithm cannot handle the case with communication delays. The information interactions among each agent and its neighbors are only at some sampling moments, while in Refs. [20]–[23], the information interactions of each agent with its neighbors are continuously required.
In this section, the Euler–Lagrange system, the graph theory and the problem description are introduced.
The dynamic system of each agent in this study is modeled by the following nonlinear second-order Euler–Lagrange equation
 |

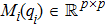
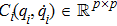
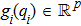


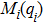
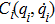
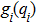
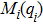
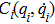
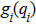
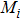
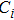
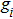
Many mechanical systems can be modeled by the Euler–Lagrange equation and the following common properties are satisfied in this study:
A directed graph 



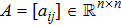


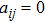










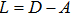


The networked MAS are composed of N agents (denoted as 
 |

In this section, the cooperative impulsive formation control algorithms for the networked Euler–Lagrange systems without and with communication delays are investigated respectively. The neural-networks approximation and adaptive technique are used to handle the system uncertain dynamics and external disturbances. The Lyapunov stability theory and Laplacian potential function in graph theory are used to prove the convergence of the system formation.
In this subsection, a cooperative impulsive formation control algorithm is designed for the networked Euler–Lagrange systems without communication delays. Firstly, the directed information interaction graph GA satisfies the following assumption.
First, the auxiliary variables are designed
 |
 |
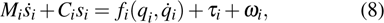 |
 |

 |

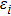
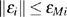
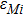
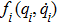
 |
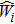
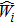
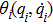

Then, we propose the following cooperative impulsive formation control algorithm
 |
 |
 |
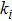
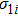
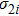
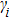
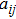
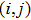
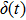
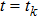
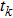
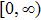
 |
Then, the following theorem is given to solve the impulsive formation control problem for the networked Euler–Lagrange systems.
To further analyze the stability of the proposed cooperative impulsive formation control algorithm for the networked Euler–Lagrange systems, the following four proof steps are given. Steps 1 and 2 are given to prove the asymptotic convergence of the networked systems when 
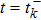


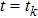
Combining Eqs. (
 |
According to the average impulsive interval definition in Ref. [29], we have
 |
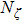
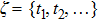
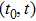
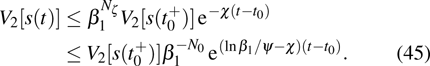 |
Using Eq. (
 |
To get the formation of the networked systems, we consider the Laplacian potential function
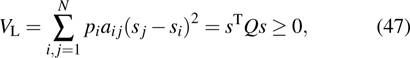 |
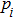
Because the information interaction graph GA among agents is strongly connected, we can obtain 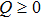


 |
Combining Eqs. (
 |
According to Lemma
 |
According to Eq. (
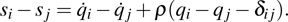 |
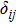
 |
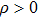
 |
 |
According to Eq. (
 |
In this subsection, the communication delays among agents are considered in the networked Euler–Lagrange systems. Since the main procedures of this subsection are similar with the former subsection, the differences are mainly stated here.
To analyze the stability of the networked systems with delays, the following Lemma is given firstly.
Then there exists a constant 
 |
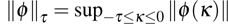
The cooperative impulsive formation control algorithm for the networked systems with communication delays is designed as Eqs. (
 |
When 
 |
Integrating both sides of Eq. (
 |
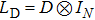

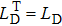
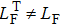
 |
The Lyapunov function 
 |
According to the inequality 

 |
Thus, equation (
 |
 |
 |
Thus, we have
 |
Let 

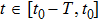
 |
 |
 |
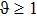
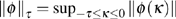
By simplifying, inequalities (
 |
 |
By the similar proof procedures in Step 4 in Subsection
In this section, a numerical simulation of satellite formation flying is presented to verify the effectiveness of the proposed cooperative impulsive formation control algorithms.
Consider a group of eight satellites (
 |
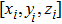
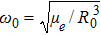
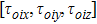


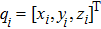

 |
This simulation’s examples assume that the relative orbit reference of the satellite formation system follows a near-circular orbit with the initial orbit elements
 |
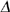
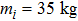
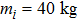
The connected directed communication topology GA among eight satellites is described in Fig.
The Laplacian matrix of the directed graph GA is
 |

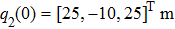
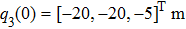
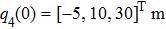

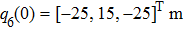
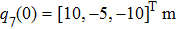
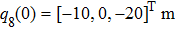

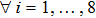
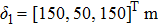
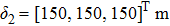
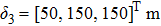
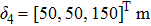
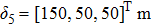


The simulation parameters of neural-networks (NN) are given as: the activation function of NN for i-th satellite used in this simulation can be denoted as
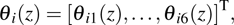 |
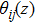
 |
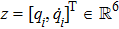
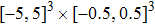
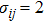
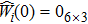
The control parameters are ρ = 0.01, 
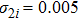



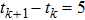
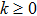
The simulation results are shown below and the figures are drawn in Figs.
To compare the control energy consumption among Case
 |
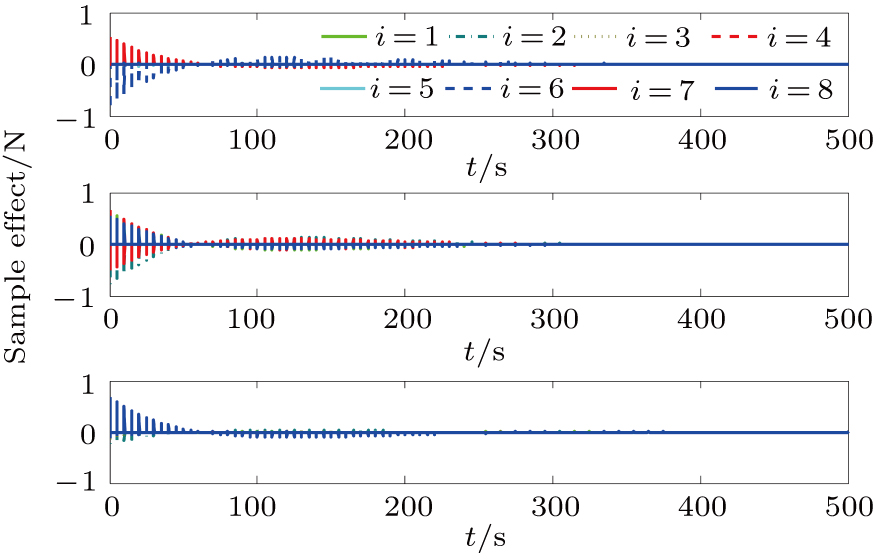
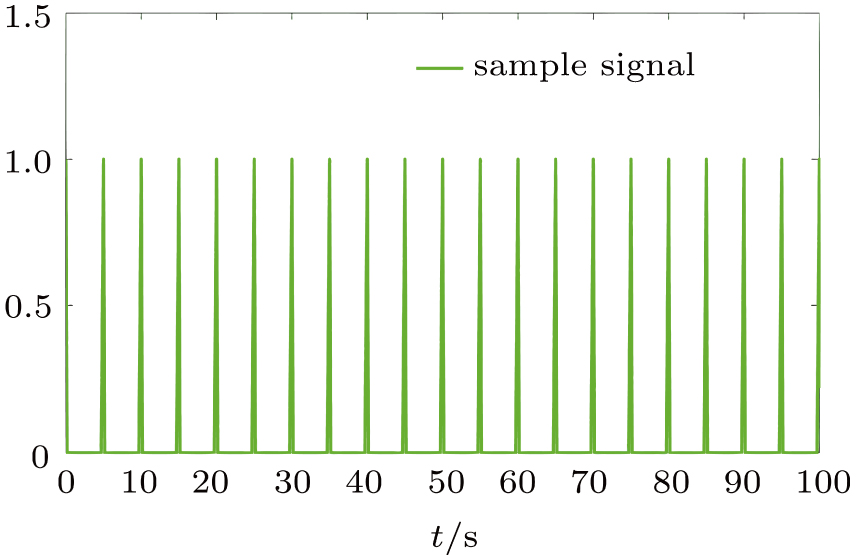
To analyze the impulsive effect on system performance, the figures of sample signal and impulsive effect in Case
We can see that the square formation of eight satellites is achieved in the above three simulation examples. Comparing Figs.
To sum up, the simulation results in Figs.
The paper focuses on the cooperative impulsive formation control problem for a class of networked Euler–Lagrange systems with uncertain dynamics and external disturbances under a connected directed graph. Furthermore, the communication delays among agents are considered. The main features of the proposed impulsive formation control algorithms are that the controllers are impulsive and the information interactions among agents are only at some discrete moments, which reduce the energy consumption and the communication frequency among agents. To handle the uncertain dynamics in the networked systems, neural-networks approximation and adaptive technique are used to compensate for the unknown nonlinear dynamics. With the proposed impulsive formation control algorithm, all agents converge to the desired formation. With the consideration of communication delays, the modified impulsive formation control algorithm is proposed. Finally, the simulation examples are presented to demonstrate the effectiveness of the proposed impulsive formation control laws and the performance improvements of impulsive formation control law upon the continuous formation control law. Future work will concentrate on the distributed impulsive leader-following formation problem with communication delays.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] |