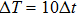† Corresponding author. E-mail:
The minimization of spurious wave reflection is a challenge in multiscale coupling due to the difference of spatial resolution between atomistic and continuum regions. In this study, a new damping condition is presented for eliminating spurious wave reflection at the interface between atomistic and continuum regions. This damping method starts by a coarse–fine decomposition of the atomic velocity based on the bridging scale method. The fine scale velocity of the atoms in the damping region is reduced by applying nonlinear damping coefficients. The effectiveness of this damping method is verified by one- and two- dimensional simulations.
Atomistic simulation is applied widely to study mechanics and materials at the nanoscale.[1] In spite of rapid development in computer techniques, atomistic simulation still suffers from limitations in terms of spatial and temporal scales. On the other hand, the continuum method is not capable of describing accurately physical phenomena at the atomic level, despite its efficiency.[2,3] Therefore, the multiscale method is proposed to overcome the limitations of those existing simulation tools, such as molecular dynamics (MD) and finite element method (FEM), so that complex phenomena at a small scale can be explored without sacrificing too much computational time. During the past decades, many multiscale methods have been developed, including concurrent coupling of length scales (CLS),[4] bridging scale method (BSM),[5–7] bridging domain method (BDM),[8] and hybrid simulation method (HSM).[9] They have been successfully used for a wide range of areas, such as nanoindentation,[10,11] crack,[12,13] and nanotribology.[14–16]
One major difficulty in multiscale coupling is that the high frequency or the short wavelength components of waves from the atomistic region cannot be captured by coarse continuum mesh. Those components that fail to propagate appropriately into the continuum region are reflected back into the atomistic region at the atomistic/continuum interface, resulting in a spurious increase of temperature. This phenomenon is known as spurious wave reflection,[17] which can generate considerable numerical errors. Recently, several multiscale techniques have been applied to handle the spurious wave reflection with varying degree of effectiveness. Cai and coworkers[18] proposed a time-dependent boundary condition to minimize elastic wave reflection based on a generalized Langevin equation, and applied to one-dimensional (1D) problems. The method requires a numerical calculation of response functions, which could be time-consuming for multiple dimensions. Wagner and Liu[5] developed a so-called bridging scale method (BSM) in which the displacement is decomposed into the coarse and fine scales by using a projection operator. They eliminated unwanted reflections by analytically accounting for high-frequency components of waves as an additional force term in the standard MD equation. However, the implementation of the BSM is not straightforward as both Fourier and Laplace transforms are needed as well as the storage of the boundary atom displacement history. Sadeghirad and Liu[19] added a viscous term into the motion equation of MD in order to reduce the non-physical reflections at the MD/FEM interface. Their damping algorithm performed well in the frameworks of BSM and BDM. Other effective methods have been developed so far, including non-reflection interfaces by E and Huang,[20] ‘stadium’ damping method by Qu et al.,[21] spatial filters by Ramisetti et al.[22]
In this study, a new damping boundary condition is proposed to remove the spurious wave reflection that occurs in atomistic-continuum coupling. In this method, firstly, we use a projection operator proposed by Wagner and Liu[5] to separate the total velocity of each atom within the overlapping subdomain of atomistic and continuum domains into coarse and fine components. The coarse velocities of the atoms are not modified so all data of mechanical deformation can be propagated into a continuum region. On the other hand to reduce the spurious reflections the fine velocities are eliminated by applying the damping coefficients. One key result in this paper is that the damping coefficients ramp nonlinearly over the width of the overlapping domain. The method is implemented by a multiple-time-step algorithm. The good performance of the proposed method is verified by one- and two- dimensional problems.
Figure
 | Fig. 1. Schematic diagram of one-dimensional multiscale coupling between FEM and MD with a damping region. |
We start by a brief introduction of the coarse-fine decomposition following Wagner and Liu’s work[5] in Subsection
According to the original bridging scale method (BSM),[5] the total displacement 
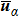

 |
As the coarse scale 
 |
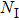
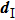
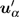
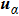
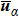
 |
Solving Eq. (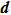
 |
Multiplying 
 |
The projection matrix is defined as
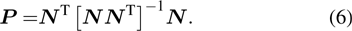 |
Therefore, the coarse scale is the least-square fit of the total scale. The fine scale is obtained by subtracting the coarse scale 

 |
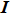
 |
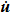
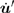
 |
Finally, the equation of the total velocity for the atoms in the damping region can be written as
 |
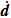

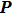
After the coarse–fine decomposition of the velocities for the atoms in the damping region, the fine velocities 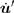


 |
Each element of the vector θ corresponds to the damping coefficient of each atom in the damping region. For the model in Fig. 
 |
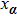
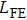
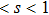
In the damping region, the continuum mesh is not refined down to the atomistic level when using the damping method. This allows a larger time step used in the FEM region compared to that in the MD region, and saves the computation time. A multiple-time-step algorithm is proposed as follows. We define the MD time step and the FEM time step as 
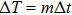

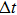
 |
 |
 |

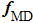
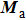
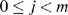
In each MD time step, the fine velocities of the atoms in the damping region are obtained according to Eq. (
After the quantities 


 |
 |
 |
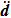
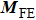
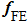
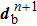

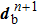
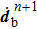
 |
 |
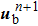
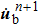
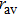
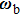
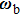
 |
The given distance 

 |

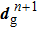
In the one-dimensional example, we apply the damping method proposed in Section
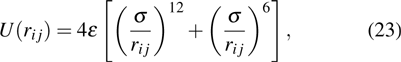 |


 |
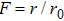
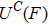
The entire region consists of 271 atoms in total, 35 atoms in the damping region, and 42 linear elements of equal size 



 |
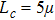
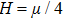
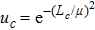
In the damping method of this study, the parameter s has a crucial effect on the reduction of the spurious wave reflections. An a priori test is used to determine the optimal parameter s.
We choose four different values of 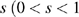
 | Fig. 4. (color online) Normalized energy of the MD region as a function of time for different parameter s. |
As shown in Fig.
Similar to the bridging domain method,[8] the width of the damping region in our method also plays a role in the reduction of spurious wave reflections. As the width increases, the remaining energy in the MD region reduces as shown in Fig. 
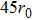



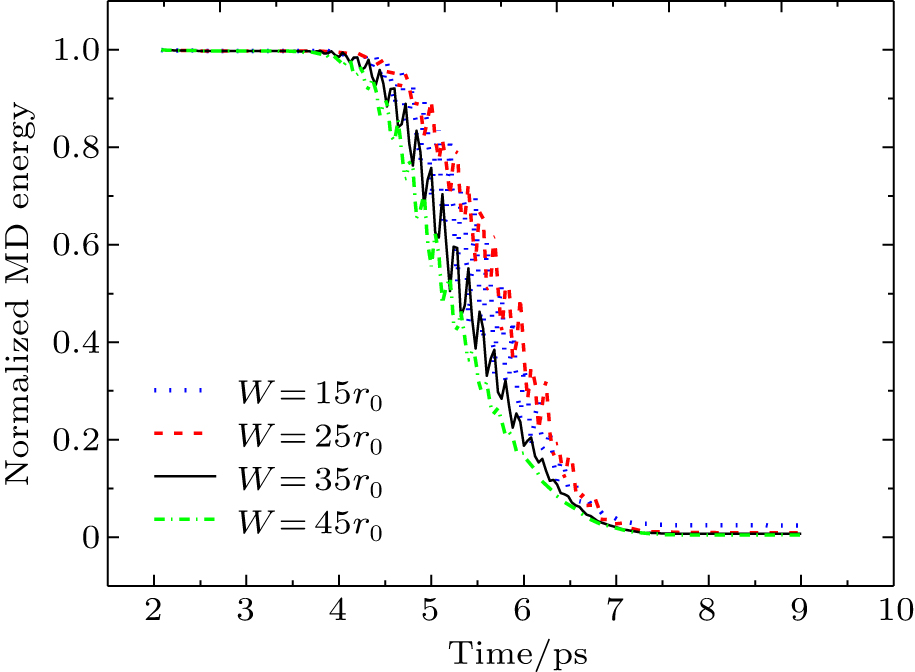 | Fig. 5. (color online) Normalized energy of the MD region as a function of time with different widths of the damping region. |
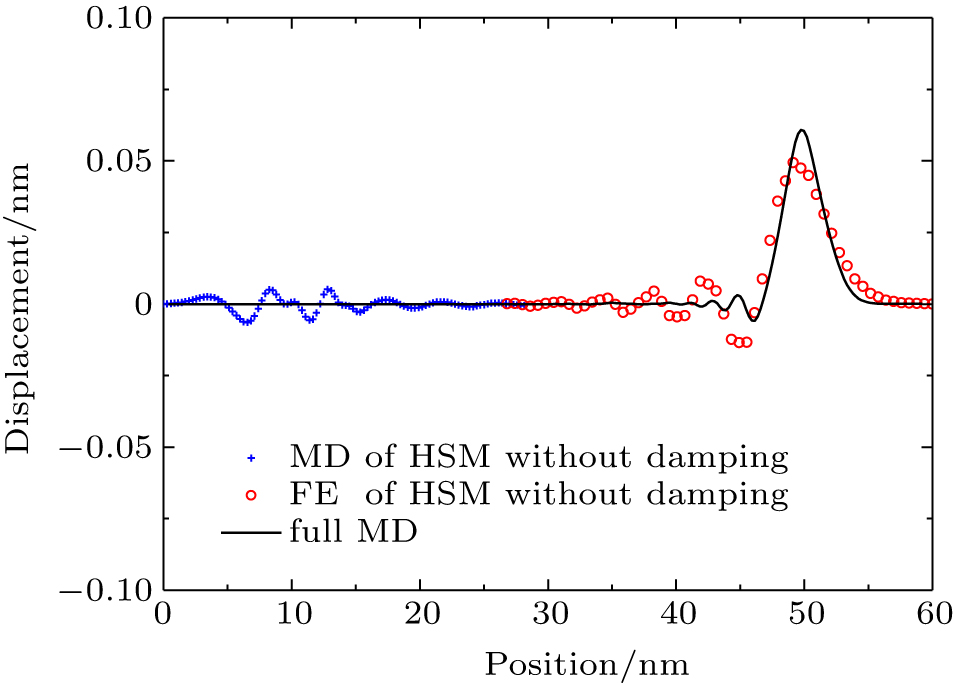
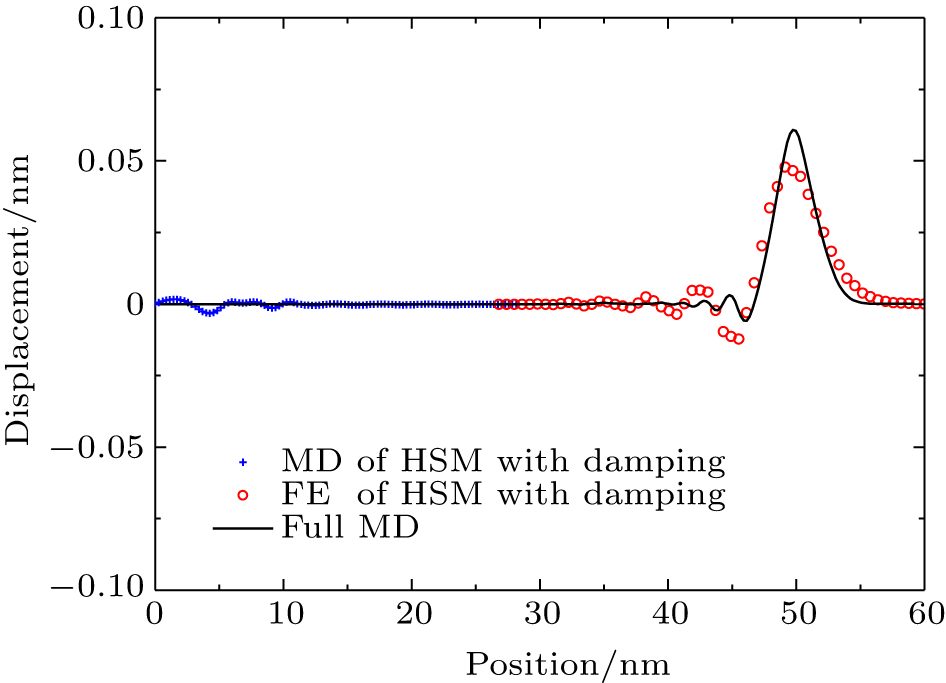
In Fig. 

In Fig.
Figure
 |
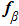
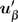
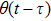
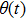
 |
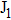
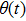
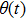
 | Fig. 8. (color online) Snapshot of displacement at t = 9 ps for the bridging scale method (BSM)[7] and the nonlinear damping method. |

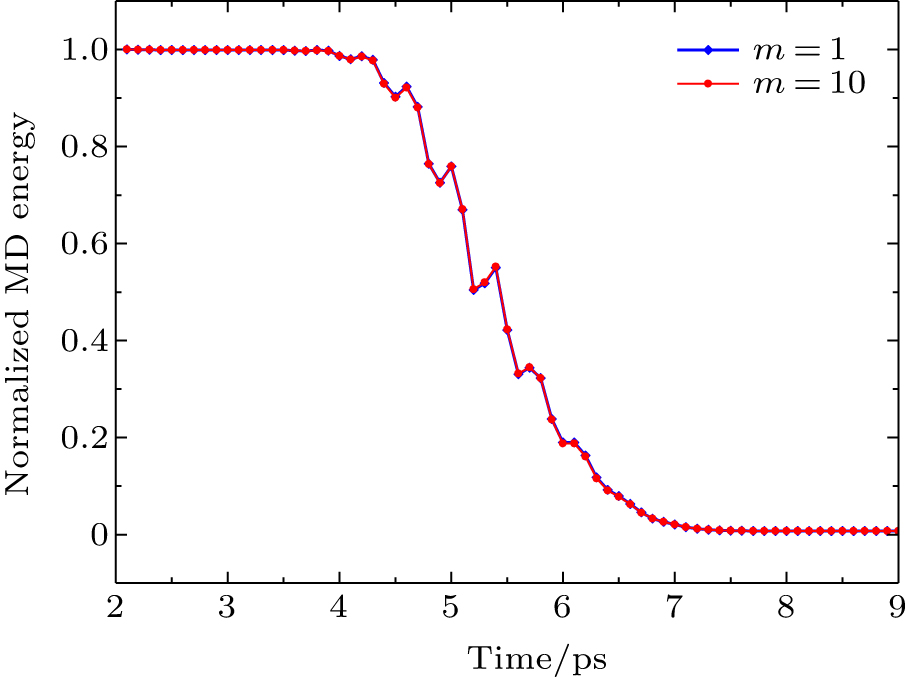
The extension of our damping method to two and three dimensions is straightforward. In this section, we apply the damping method to the pulse propagation problem, which was previously studied by Luan and Robbins using the hybrid simulation method (HSM).[9]
Figure 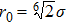



Periodic boundary conditions are applied for both MD and FEM regions along the x direction. The right boundary of the FEM region is fixed in Fig. 


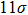
Figure
Similar to the one-dimensional example in Section
In this study, a nonlinear damping method is proposed for the reduction of the spurious wave reflection in the atomistic-continuum coupling. The damping method is based on a coarse-fine decomposition, and is performed by a stable multiple-time-step algorithm. Its effectiveness is verified by one- and two-dimensional examples with measures of displacement and MD energy. The results show that this damping method has a better performance compared to the linear damping method. Its effects on reducing the spurious wave reflections are comparable to the THK in the bridging scale method, but its implementation is more straightforward. The successes in two-dimensional cases indicate that the nonlinear damping method is practical and not limited to one dimension. The extension of our method to three dimensions will be carried out in the future.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] |