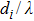Cite this Article
Khan SU, Rahim MKA. Correction of failure in antenna array using matrix pencil technique. Chinese Physics B, 2017, 26(6): 068401  
Permissions
Correction of failure in antenna array using matrix pencil technique
Khan SU †, Rahim MKA ‡
Advanced RF & Microwave Research Group, Department of Communication Engineering, Faculty of Electrical Engineering, Universiti Teknologi Malaysia, 81310 Skudai, Johor, Malaysia

 

† Corresponding author. E-mail: shafqatphy@yahoo.com mdkamal@utm.my

Project sypported by the Research Management Centre (RMC), School of Postgraduate Studies (SPS), Communication Engineering Department, Faculty of Electrical Engineering (FKE), Universiti Teknologi Malaysia (UTM), Johor Bahru (Grant Nos. 12H09 and 03E20).

Abstract

In this paper a non-iterative technique is developed for the correction of faulty antenna array based on matrix pencil technique (MPT). The failure of a sensor in antenna array can damage the radiation power pattern in terms of sidelobes level and nulls. In the developed technique, the radiation pattern of the array is sampled to form discrete power pattern information set. Then this information set can be arranged in the form of Hankel matrix (HM) and execute the singular value decomposition (SVD). By removing nonprincipal values, we obtain an optimum lower rank estimation of HM. This lower rank matrix corresponds to the corrected pattern. Then the proposed technique is employed to recover the weight excitation and position allocations from the estimated matrix. Numerical simulations confirm the efficiency of the proposed technique, which is compared with the available techniques in terms of sidelobes level and nulls.

PACS: 84.40.Ba;84.40.Xb;33.20.Bx
Keyword:array correction;low rank estimation;matrix pencil technique;singular value decomposition
1. Introduction

In this work, we put an emphasis on the problem of failure correction in antenna arrays. In a communication system there is a possibility of getting failure of sensors. The failure of a sensor can damage the power pattern in terms of sidelobes, null depth and shifting of nulls from their original positions. Due to this failure, the communication becomes a haze. To obtain the desired pattern with the active number of sensors is very important in the case of radar and satellite communication.[1] This technique focuses on achieving the desired power pattern even in the case of sensor failure. Identification and correction of failures in an antenna array has received more attention in recent years. Once the locality of a damaged sensor is identified by fault-finding techniques,[2–8] some correction techniques can be used to obtain the desired power pattern.[9–17] Recently, Zhu et al. designed an algorithm for the detection of damaged antenna arrays and this technique[8] requires no prior knowledge of the damaged sensors.

Some available techniques have been applied to the correction of failure by changing the weights of the active sensors in the antenna array by using nature-inspired heuristic optimization techniques to achieve the desired pattern.[11–13] However, these available techniques require active sensors in the antenna array to obtain the desired power pattern because of the constraint of uniform sensor spacing. Peters[14] proposed a conjugate gradient technique to reconfigure the weights and phase distribution of the active sensors in the array by reducing the average SLL only. Lorenzo et al.[15] proposed a technique based on a time modulated array (TMA) for the correction of failure. In the correction of faulty arrays, with the reduction of SLL, a null steering and beam steering becomes an important issue to be addressed. Hejres et al.[16,17] presented compensation for sustaining fixed nulls and null steering in phased array antenna. Acharya et al. proposed a method for failure compensation in faulty arrays. The first part of his study dealt with the thinning in the faulty arrays, i.e., to find a limit to the least number of working sensors of the array that can recover the desired pattern while the second part dealt with the maximum number of faulty sensors that can be compensated for by using particle swarm optimization,[18] but this method only reduces the SLL. Yeo and Lu proposed a genetic algorithm for failure correction which reduces the sidelobes level only.[19] The symmetrical linear array is of great importance, which has already shown useful results to achieve the desired pattern for failure correction, where the failed sensor signal is reconstructed from the failed sensors by taking its conjugate.[20] Array antenna provides higher gain and has many applications in the field of engineering and technology.[2–23]

Some of the optimization algorithms such as cultural algorithm with differential evolution (CADE),[6] particle swarm optimization (PSO) method,[12] cuckoo search algorithm,[13] genetic algorithm along with pattern search (GAPA),[24] analytical methods,[16,17] and other synthesis techniques[14,15] have used the active sensors in antenna arrays for failure correction but none of them can obtain the desired pattern with the reduced number of sensors by matrix pencil technique (MPT). Although the obtained desired pattern with nature-inspired evolutionary algorithms is capable of correcting the failure, it is time consuming. The failure correction of sensors by MPT is an interesting and efficient way to obtain the desired power pattern with the reduced number of sensors. The MPT[25,27] readjusts the weight and position for the original pattern with the reduced number of sensors. The SVD technique is used for the non-uniform and reduced number of signal sampling.[28–30]

In this paper, a non-iterative technique is developed for the correction of array failure based on matrix pencil technique (MPT). The failure of sensors in antenna array can damage the whole radiation pattern. In the developed technique, the radiation pattern of the damaged array is sampled to form a discrete power pattern information set. Then this information set can be arranged in the form of Hankel matrix (HM) and execute the singular value decomposition (SVD). By removing the non-principal values, we obtain an optimum lower rank estimation of the HM. This lower rank matrix corresponds to the desired pattern. Then the proposed technique is employed to recover the weight excitation and position allocations from the estimated matrix. The proposed MPT provides better power pattern than the conventional techniques with fewer number of sensors. The remaining paper is organized as follows. The problem formulation is defined in Section 2 while the proposed solution is described in Section 3. Then in Section 4 the simulation results of the proposed method are presented. Finally, some conclusions are drawn in Section 5.

2. Problem formulation

Consider a linear antenna array consisting of N number of sensors. The healthy array factor for this setup is given by[31]

where Ai is the weight excitation of the i-th sensor positioned at and is the wave number. The non-healthy setup for this damaged antenna array can be given by the following expression:
It is assumed that the sensors A1, A2, and A5 become damaged in the antenna array. One can clearly see from Fig. 1 that due to A1, A2, and A5 sensor failure, the whole power pattern is damaged in terms of sidelobes, null depth and null positions shifting from the original locations. So, the main objective of this work is to correct the failure pattern with the reduced number of sensors that has the same desired pattern as the healthy one .

Fig. 1. (color online) Original and damaged sensor radiation power pattern.
3. Proposed solution

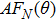
The proposed method is based on the matrix pencil technique (MPT) to correct the failure pattern with the reduced number of sensors. The solution to this problem is given by the following cost functions:

where and are the weight excitation and locations for the corrected C number of antenna sensors. In this work, a non-iterative technique is used for failure correction in antenna arrays. The method consists of two stages. In the first stage, the singular value decomposition (SVD) method is used to obtain low rank approximation in least square estimation of the HM constructed by the array power pattern samples. The lower rank matrix corresponds to the corrected pattern that is comprised of a reduced number of antenna sensors. In the second stage, an MPT is used to reconfigure the weight excitations and locations of the sensors in antenna array. The array factor is defined by Eq. (1) and let and . The array factor in Eq. (1) can be written as
So, our desire is to set a few antenna sensors to obtain the original pattern . In signal processing, the MPT is useful for the problems like the array factor defined in Eq. (1). Now the procedure to select the minimum number of sensors C of the corrected array in Eq. (3) is as follows. To sample the pattern in the identical steps from u = −1 to u = +1, where the sample length is 2M+1,
where . As per Nyquist theorem, the sampling rate must be i.e., . As we consider N number of sensors in the antenna array with a spacing of , we require sample points for the array radiation pattern. The HM that is built up from the sample data of the radiation power pattern is given as follows:
where . The parameters M and K are chosen as follows: , and . For instance, we set that, N = K = M, then SVD of the matrix is
where , , and are the singular values of . .

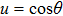
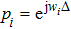
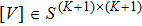
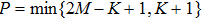
The rank of the HM and the number of nonzero singular values should be equal to the number of exponentials. In other words, there will be N nonzero singular values for the N number of sensors in the antenna array. To obtain the lower rank estimation of , we set the non-principal values to be zero, which resembles the array with reduced number of sensors C.

where and .
From Eq. (9), the error decreases as the number of sensors C increases and approaches to zero when C = N. This implies that the radiation power pattern of the corrected array achieves a better estimation of the original array. In a normal scenario, expression for the corrected pattern of minimum number of sensors C can be written as follows:
where ε is a small number and the setting of this positive number is dependent when the corrected pattern matches the original pattern. When the lower rank matrix YC is reconstructed, the parameters equivalently corresponding to the locations of the corrected array C can be obtained by determining the eigenvalue problem
where is obtained from by removing the first column that is achieved by removing the last one. The value is the location of the new element of the array obtained by the proposed method of recovering the desired pattern. The values are equal to the nonzero eigenvalues. When we obtain the values , the location of the sensors are given by[16]
Thus the estimated weights and locations obtained by the proposed MPT are given by
where .

4. Simulation results

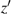
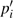
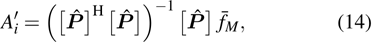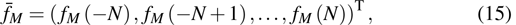In this section, different numerical simulations for failure correction are carried out to confirm the validity of the proposed matrix pencil technique (MPT). Three types of patterns are considered for the recovery of the desired pattern.

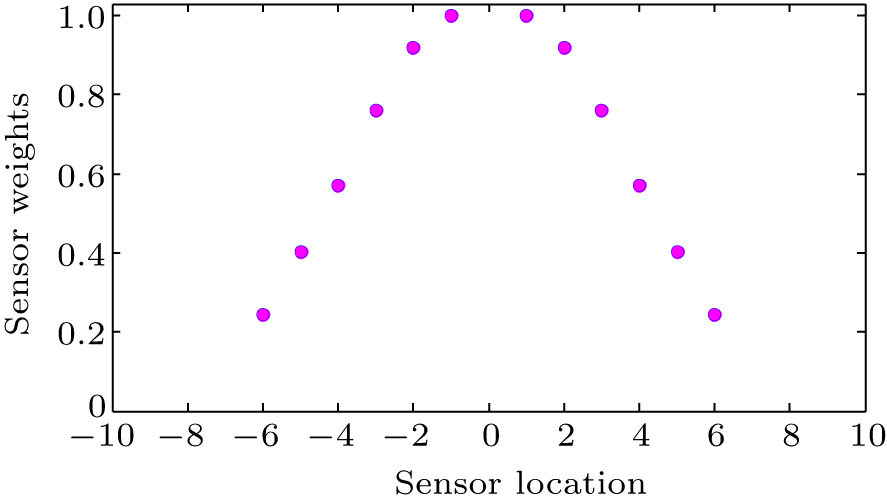
4.1. Case A: Recovery of Chebyshev pattern

In this case, the failure correction by matrix pencil technique (MPT) is carried out with a minimum number of sensors. The matrix pencil is a non-iterative technique which is used for performing the correction in a linear antenna array to reduce the sidelobe level and null depth level and for keeping the main beam in the direction of desired users. The MPT starts with generating an HM with uniformly-spaced samples from an identified far field beam pattern. A singular value decomposition (SVD) along with conditions to find the number of principal singular values determines a corrected pattern with reduced number of sensors. First, consider a Chebyshev power pattern of N = 20 number of sensors with sidelobe level SLL = -30 dB as shown in Fig. 2 and assume that N = M for the sampling parameter. As we have seen that due to the failure of sensors the whole power pattern is disturbed as shown in Fig. 1 and communication becomes a haze in certain cases like radar and satellite communications. But by applying the proposed MPT, the failures can be recovered.

Fig. 2. (color online) Original Chebyshev array and the corrected array beam patterns by MPT.

The Chebyshev samples of singular value spectrum is shown in Fig. 3 and these values are reduced in magnitude. The greater values in magnitude of singular value spectrum (SVS) are taken which correspond to the number of sensors in the corrected array while the smaller values are fixed to be zero. Thus the corrected pattern can be obtained by fewer number of sensors in the array by using the proposed method called MPT. The weights and locations of the original faulty and corrected array are shown in Table 1. The condition for the minimum number of sensors in the corrected array are set by Eq. (10). We make an assumption that an array contains 20 sensors, and 40% of sensors are damaged in the array due to some reason. Because of these failures, the whole power pattern is disturbed in terms of sidelobes, nulls and shifting of nulls from their original locations. Now our desire is to recover the pattern by the proposed method called MPT which has the same pattern as that of the original one. By applying the proposed MPT, the corrected pattern is recovered with C = 12 number of sensors at . This is the least square error obtained by Eq. (10) for recovering the desired pattern. Figure 2 shows the comparison between the original Chebyshev pattern and the corrected pattern obtained by the proposed MPT. The uniform weights of the Chebyshev array and the non-uniform weights of the corrected pattern obtained by the proposed MPT are given in Table 1. The proposed MPT recovers the same pattern as that of the original Chebyshev pattern obtained by 20 sensors. Figure 3 shows the singular values of HM in the decreasing order of magnitude. The first 12 greater singular values are taken which relate to the number of sensors in the corrected array while the remaining values are fixed to zero. The weights and sensor locations of the corrected array are given in Table 1.

Fig. 3. (color online) Singular values of Hankel matrix.
Table 1.

Weights and locations of uniform Chebyshev array and corrected non-uniform array.

.

Figure 2 shows the comparison between the original and the corrected array beam patterns and both arrays approximately give the same results. After applying the proposed technique, the corrected pattern overlaps the original Chebyshev pattern as depicted in Fig. 2. The weights of the corrected pattern obtained by proposed MPT are shown in Fig. 4.

Fig. 4. (color online) Weights of the corrected array obtained by proposed MPT.
4.2. Case B: Recovery of Taylor pattern

In this case, we consider a Taylor array pattern of 32 sensors with SLL = −25 dB as shown by the blue solid lines in Fig. 5. Again we assume a failure of 40% of sensors in the uniform Taylor array. Due to these failures, the sidelobe level and nulls are damaged. After applying the proposed MPT, the same pattern is recovered into that of the original Taylor array. The weights of the corrected array obtained by the proposed MPT is depicted in Fig. 6. The corrected pattern weights and locations are compared with those of the original Taylor array (table 2). The original Taylor array and corrected pattern obtained by proposed MPT are shown in Fig. 5. The corrected pattern overlaps the original pattern. The weights obtained by the proposed MPT are shown in Fig. 4.

Fig. 5. (color online) Original Taylor pattern and the corrected array beam patterns by proposed MPT.
Fig. 6. (color online) Corrected array weights of 18 sensors.
Table 2.

Weights and locations of uniform Taylor pattern and proposed corrected array by MPT.

.

The corrected array of 18 sensors is tapered a little as shown in Fig. 7. The sensors spacing varies from 0.90 at the centre to 0.85 wavelengths at the array ends and the spacing is symmetric about the array centre. As we have observed, due to the failure of sensors, the power pattern is damaged in terms of main lobe and sidelobes level but after applying the proposed MPT, the corrected pattern has the same main lobe and sidelobes level as those of the original Taylor array. The weights of the original Taylor array, damaged Taylor array, and Taylor array obtained from the proposed MPT are given in Table 2.

Fig. 7. (color online) Corrected array sensor spacing obtained by MPT.

From Fig. 6 it is clear that the corrected array weights of 18 sensors decrease from 1.00 at the center to 0.23 at the ends and the array is symmetric about the centre.

Now we consider a large Taylor array of 64 sensors with sidelobe level −30 dB and assume that 40% of sensors are faulty in the array. The failure is produced in sidelobes level and damages the nulls. The Taylor pattern is shown by the blue solid lines while the corrected pattern obtained by proposed MPT is given by red solid lines as shown in Fig. 8. The corrected pattern is obtained by the proposed MPT from 34 sensors as shown in Fig. 9 and the corrected pattern overlaps the original Taylor pattern in terms of sidelobes, nulls and main beam.

Fig. 8. (color online) Original Taylor pattern (−30 dB, n = 3) of 64 sensors and the corrected array beam pattern by proposed MPT.
Fig. 9. (color online) Corrected array weights obtained by proposed MPT from 34 sensors.

The weights of the corrected array of 34 sensors obtained by the proposed MPT are symmetrical about the centre of the array. The corrected array weights decrease from 1.00 to 0.22 at the array ends which is shown in Fig. 9. The original Taylor array simulated patterns for 64 sensors and the pattern obtained by the proposed MPT from 34 sensors are the same. Both the original and corrected patterns are approximately the same in terms of sidelobes and main beam.

4.3. Case C: Analysis of comparison between conventional and proposed MPT

The performance of the proposed MPT is compared with that from the available technique.[19] In this case, we consider a linear array of 32 sensors with sidelobes level −25 dB as the test antenna. The failure is assumed to occur at location , and due to this failure, the pattern is disturbed in terms of sidelobes, nulls and positions of nulls which are shifted from the desired location as shown by the pink solid lines in Fig. 10. In Ref. [19] the desire is to recover the sidelobe level only by varying the weights of the active sensors but the null depth level and location of nulls to their original locations are still problems to be taken into account. Our proposed MPT deals with the problems of sidelobes, null depth level and location of nulls toward the desired direction. The sidelobes and null depth level of the original, damaged, conventional technique in Ref. [19] and proposed MPT are given in Table 3. From Fig. 10 it is obvious that the conventional technique in Ref. [19] recovers the sidelobes only but the proposed MPT overlaps the desired power pattern and obtains the same power pattern as that of the original Chebyshev array.

Fig. 10. (color online) Analysis of comparison between conventional technique in Ref. [19] and proposed MPT.
Table 3.

Analysis of comparison between the proposed MPT and conventional technique in Ref. [19].

.

If the desired target changes its location, then the main beam can be steered in the target direction. The main beam direction in this scenario is directed at an angle of . One can clearly observe from Fig. 11 that for the pattern obtained by the proposed MPT, its main beam direction is steered along with the nulls at the desired angles. The pattern obtained by the proposed MPT is given by the black dotted lines and the conventional technique[19] by the red solid lines.

Fig. 11. (color online) Main beam steering at an angle 52° by the proposed MPT and conventional technique in Ref. [19].

Now if the target changes its location, then by the proposed MPT the main beam direction can be steered at an angle 138° along with the nulls as shown in Fig. 12. The weights of the original technique, conventional technique in Ref. [19] and proposed MPT for Fig. 11 are given in Table 4.

Fig. 12. (color online) Main beam steering at angle 138° by the proposed MPT and conventional technique in Ref. [19].
Table 4.

Analysis of comparison between proposed MPT and conventional technique.

.
5. Conclusions

In this paper, a non-iterative effective technique for failure correction in antenna array is developed. Due to sensor failure, the whole radiation patterns are disturbed in terms of sidelobes and main beam. Through the achievement of the singular value decomposition (SVD) of radiation power pattern samples, we can find the minimum number of sensors in the corrected array which has the same pattern as that of the original array. After that, the MPT is used to find the weights and locations of sensors of the corrected array. The failure of sensors in the array is 40%. By applying the proposed technique, the desired pattern is recovered by the non-uniform array with the fewer number of sensors than by the uniform Chebyshev array. The proposed technique is very suitable for failure correction in the case of large antenna arrays where we require narrow beam and low sidelobe level. This method can be extended to circular and planar arrays.

Reference
[1] Balanis C A 2005 Antenna Theory: Analysis and Design 3 New York Wiley
[2] Khan S U Qureshi I M Haider H Zaman F Shoaib B 2016 Wireless Personal Commun. 91 383
[3] Khan S U Qureshi I M Naveed A Shoaib B Basit A 2015 J. Sensors 2016 6139802
[4] Khan S U Qureshi I M Zaman F Khan W 2017 Frontiers of Information Technology & Electronic Engineering 18 235
[5] Khan S U Qureshi I M Zaman F Basit A Khan W 2013 World Appl. Sci. J. 26 232
[6] Khan S U Qureshi I M Zaman F Shoaib B Ashraf K 2015 Proceedings of 12th International Bhurban Conference on Applied Sciences and Technology, IEEE IBCAST, 2015 629
[7] Choudhury B Acharya O P Patnaik A Bacteria 2013 International Journal of RF and Microwave Computer-Aided Engineering 23 141
[8] Zhu C Wang W Q Chen H So H C 2015 IEEE Sensors Journal 15 3773
[9] Khan S U Qureshi I M Zaman F Naveed A Shoaib B Basit A 2014 The Scientific World Journal 2014 852539
[10] Khan S U Qureshi I M Shoaib B 2015 Mehran University Research Journal 4 325
[11] Rodríguez J A Ares F Moreno E Franceschett G 2000 Electron. Lett. 36 196
[12] Acharya O P Patnaik A Sinha S N 2011 Applied Computational Intelligence and Soft Computing 2011 692197
[13] Khan S U Qureshi I M Shoaib B Basit A 2015 Proceedings of 12th International Bhurban Conference on Applied Sciences and Technology, IEEE IBCAST, 2015 633 636
[14] Peters T J 1991 IEEE Trans. Anten. Propag. 39 1497
[15] Poli P Rocca L Oliveri G Massa A 2014 IET Radar. Sonar & Navigation 8 195
[16] Hejres J A Peng A Hijres J 2007 IEEE Anten. Wireless Propag. Lett. 6 332
[17] Hejres J A 2004 IEEE Trans. Anten. Propag. 52 2891
[18] Acharya O P Patnaik A Sachendra N S 2014 International Journal of RF and Microwave Computer-Aided Engineering 24 635
[19] Yeo B K Lu Y 1999 IEEE Trans. Anten. Propag. 47 823
[20] Zaman Fawad Qureshi Ijaz Mansoor Munir Fahad UllahKhan Zafar 2014 Chin. Phys. 23 078402
[21] Tang Z L Yu L J Li S M 2016 Acta Phys. Sin. 65 070701 in Chinese
[22] Han Y J Zhang J Q Li Y F Wang J F Qu S B Zhang A X 2016 Acta Phys. Sin. 65 147301 in Chinese
[23] Khan S U Qureshi I M Shoaib B Naveed A 2016 J. Inform. Sci. Eng. 32 611
[24] Khan S U Qureshi I M Zaman F Naveed A 2013 Prog. Electromagn. Res. 52 165
[25] Liu Y Nie Z Liu Q H 2008 IEEE Tran. Anten. Propag. 56 2955
[26] Hua Y Sarkar T K 1990 IEEE Trans. Acoust., Speech, Signal Proces. 38 814
[27] Sarkar T K Pereira O 1995 IEEE Anten. Propag. Mag. 37 48
[28] Caille G Cailloce Y Guiraud C Auroux D Touya T Masmousdi M 2007 2nd Eur. Conf. Antennas and Propagation November 11–16, 2007 Edinburgh, U.K. 23
[29] Mazzarella G Panariello G 1994 Proc. IEEE AP-S. Int. Symp. June, 1994 Seattle, WA Vol. 1 505 506
[30] Anderson J B 2000 IEEE J. Sel. Areas Commun. 18 2172
[31] Wolf I 1937 Proc. IRE 25 630