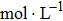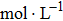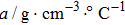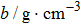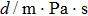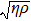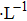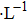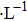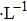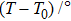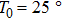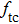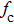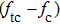† Corresponding author. E-mail:
The quartz crystal microbalance (QCM) is an important tool that can sense nanogram changes in mass. The hybrid temperature effect on a QCM resonator in aqueous solutions leads to unconvincing detection results. Control of the temperature effect is one of the keys when using the QCM for high precision measurements. Based on the Sauerbrey’s and Kanazawa’s theories, we proposed a method for enhancing the accuracy of the QCM measurement, which takes into account not only the thermal variations of viscosity and density but also the thermal behavior of the QCM resonator. We presented an improved Sauerbrey equation that can be used to effectively compensate the drift of the QCM resonator. These results will play a significant role when applying the QCM at the room temperature.
A quartz crystal microbalance (QCM) measures the mass variation per unit area by measuring the change in frequency of a quartz crystal resonator. The changes in mass deposited on the crystal surface are directly reflected in changes of the resonator frequency. In 1959, Sauerbrey first developed a method for measuring the resonator frequency of the QCM resonator in air using an oscillator circuit.[1] In 1985 Sauerbrey’s method was further developed by Kanazawa for measuring viscosity and density of a liquid.[2] Both methods continue to be used in nearly all applications as the primary tool in QCM resonator experiments for conversion of frequency to mass.[3]
A QCM sensor typically consists of an oscillator circuit containing a thin AT-cut quartz disk with circular electrodes on both sides of the quartz. Due to the piezoelectric properties of the quartz material, an alternating voltage between these electrodes leads to mechanical oscillations of the crystal. The resonant frequency of the quartz is directly affected by the thermal changes.[4,5] When a QCM resonator contacts liquids, both the accumulation of rigid mass and changes in the property of the liquid, e.g., density and viscosity, contribute to the frequency shift. The density and viscosity of solutions have a strong dependence on temperature.[6] Thus, the methods of Sauerbrey and Kanazawa are inappropriate for liquid measurement when considering the temperature effect. Control of the temperature effect is key when applying the QCM for high accuracy measurements. As we know, four methods are typically used to control the temperature effect on the measurements. First, keep the quartz crystal[7–9] sensors at a constant temperature by placing them in a temperature-controlled container. Second, use an additional reference crystal,[10–12] that is protected from mass changes yet experiences temperature changes identical to the measurement crystal. This is called the dual crystal method. Third, the baseline subtraction method uses QCM resonator data before and after the measurement,[13] which assumes that the drift of the QCM resonator baseline caused by the temperature effect can be modeled.[14] Fourth, compensate for the drift using analog or digital voltage.[15] However, when considering these 4 methods, the temperature of the liquid cannot be controlled for several possible applications (e.g., sea-water immersed sensor). The “dual crystal method” is difficult to employ due to the many temperature effects caused by transient temperatures that the reference crystal may not detect.[16] Furthermore, to compensate for drift using analog or digital voltage would be inaccurate due to the amplitude-frequency effect,[17] which denotes the variation in frequency with respect to the crystal[18–20] current after the temperature effect has been eliminated. In addition, the effect of change in a solution’s density and viscosity induced by temperature is not taken into account.
In this paper, we discussed a problem concerning the hybrid temperature effect on a QCM resonator in aqueous solutions. Based on the Sauerbrey’s and Kanazawa’s theories, we then proposed a method for enhancing the accuracy of the QCM measurement, which takes into account not only the thermal variations of viscosity and density but also the thermal behavior of the QCM resonator.
According to Sauerbrey’s theory, the rigid attachment of a film of mass 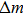
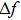
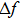
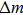
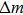
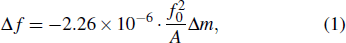 |
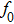
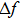

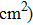
To analytically describe the frequency-temperature behavior, the measured change of frequency versus temperature can be developed in a power series, determined by first, second, and third-order temperature coefficients.[21–23] It can be expressed by Eq. (
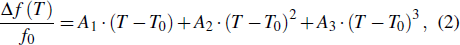 |
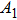
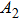
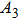
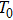
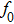

According to Kanazawa, if a Newtonian liquid is in contact with one of the QCM resonator surfaces, the resonator frequency change is proportional to the square root of the product of viscosity and density.[2] This can be expressed by Eq. (
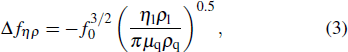 |
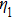
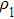
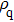

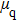
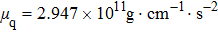
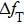
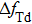
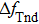

In the experiments, three identical 8-MHz AT-cut QCMs (AC8AP14, JJK Electronic Co., Ltd.,) coated with gold were used, as shown in Fig. 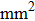
The main crystal electrode acted as a working electrode in solution, while the opposite side of the crystal was exposed to air. The electrodes were connected to an oscillator circuit using small, flat-nosed alligator clips. Tests were conducted using a frequency measuring device (EQCM-400C, Shanghai, Instruments, Inc.) which outputs ten frequencies per second, and a Lab-VIEW 2014 virtual instrument developed in the author’s laboratory. In this research, the frequency-change measurements were made using Lab-View software. The viscosity of the liquids (NaCl solutions and pure water) at different temperatures was measured using a Digital Rotary Viscometer (NDJ-8S, Shanghai Pingxuan Instrument Co., Ltd.), while the density of the liquids at different temperatures was measured using a specific gravity meter (DA-130N, Kyoto Electronics Manufacturing Co., Ltd.). The environmental temperature was directly measured during the operation of the QCM using a digital thermometer (TM-902C, LUTRON ELECTRONIC ENTERPRISE Co., Ltd.) with a sensitivity of 0.1 °C. Lastly, the temperature was controlled using an electrothermal constant temperature incubator (BEIJING KEWEI YONGXING INSTRUMENT Co., Ltd.) with a temperature sensitivity of 0.1 °C. For all experiments, three cleansers, 95% alcohol solution, 99% acetone solution, and pure water, were used sequentially to clean the QCM resonator with the ultrasonic cleaner (JP-008, Skymen cleaning equipment Co., Ltd.) for 5 min at room temperature. Then, the QCM resonator was dried using nitrogen.
We conducted three groups of experiments: i) experiments of the temperature effect on the NaCl solution; ii) experiments of the direct temperature effect on the QCM; iii) experiments of the indirect temperature effect on the QCM.
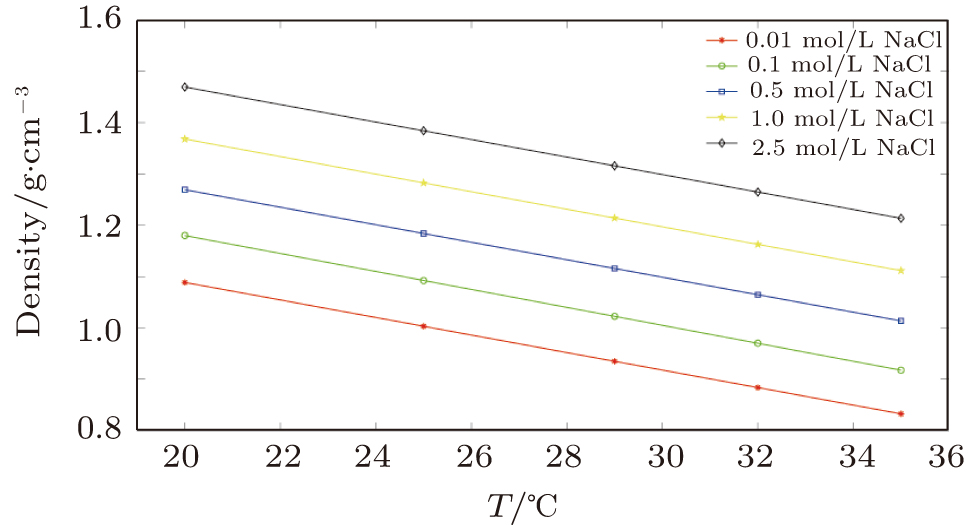
In the first group of experiments, we investigate the temperature effect on the NaCl solution, the densities and viscosities of five NaCl solutions were measured in the range of 20 °C to 35 °C.
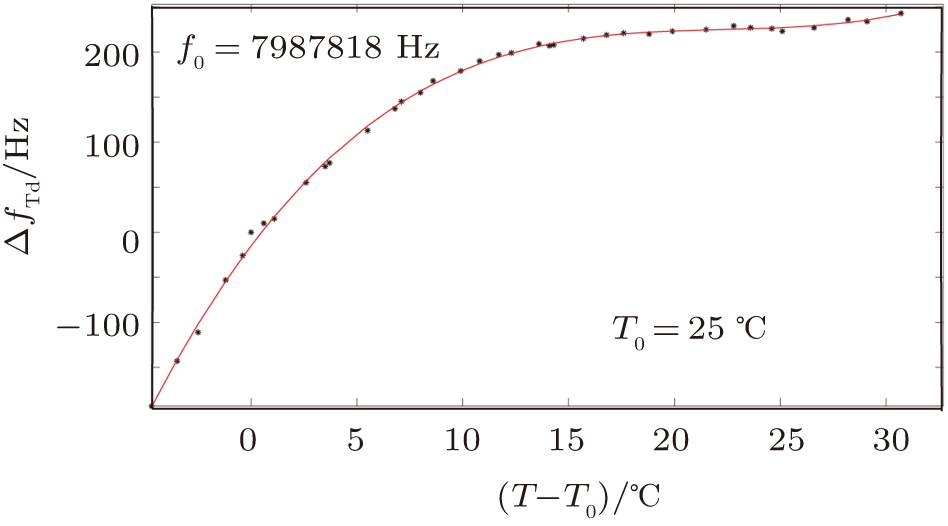
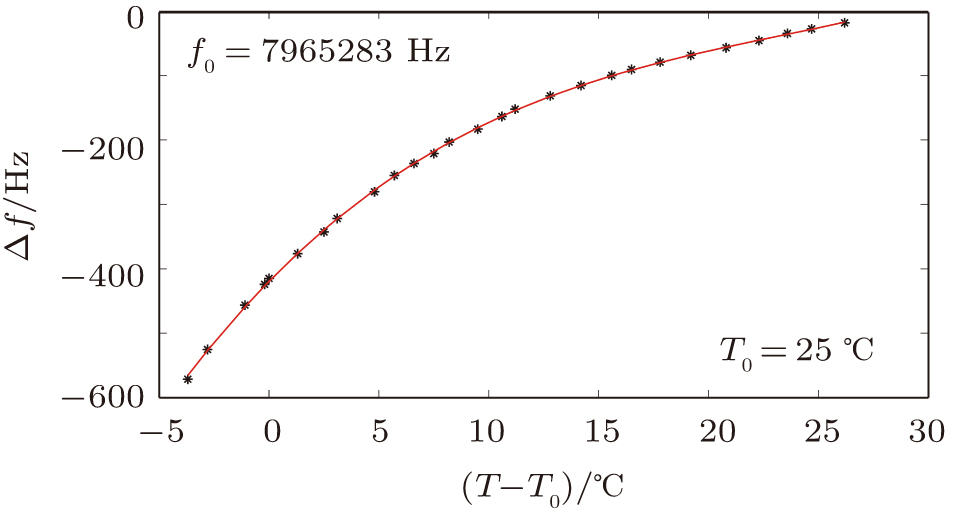
For the second group of experiments, we measured frequencies of the QCM in air and pure water. We chose 37 temperature points over the range of 20.3 °C to 55.7 °C (see Table
| Table 1.
Temperature points in analysis of temperature effect of QCM resonator in air. . |
| Table 2.
Temperature points in analysis of temperature effect of QCM resonator in pure water. . |
In the third group of experiments, we used five NaCl solutions with different concentrations (see Table
| Table 3.
NaCl solution concentrations in analysis of temperature–viscosity–density–frequency effect of QCM resonator. . |
One frequency datum was obtained for each experiment by averaging the output frequencies in a stable baseline. We averaged about 1000 or 2000 frequencies, with the EQCM-400C for a more accurate frequency change measurements. A median of five frequency data from five repetitive experiments was reported as a measuring result. In particular, all data points were taken at 25 °C.
Figures 
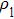
 |
| Table 4.
Density–temperature coefficients of NaCl solutions with different concentrations. . |
The viscosity (
 |
| Table 5.
Viscosity–temperature coefficient of NaCl solutions with different concentrations. . |
Figure
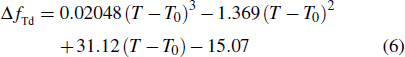 |
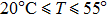
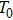
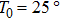
According to Eq. (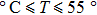
Figure 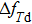

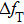
Figure 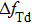
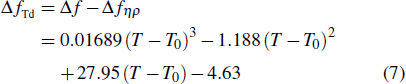 |
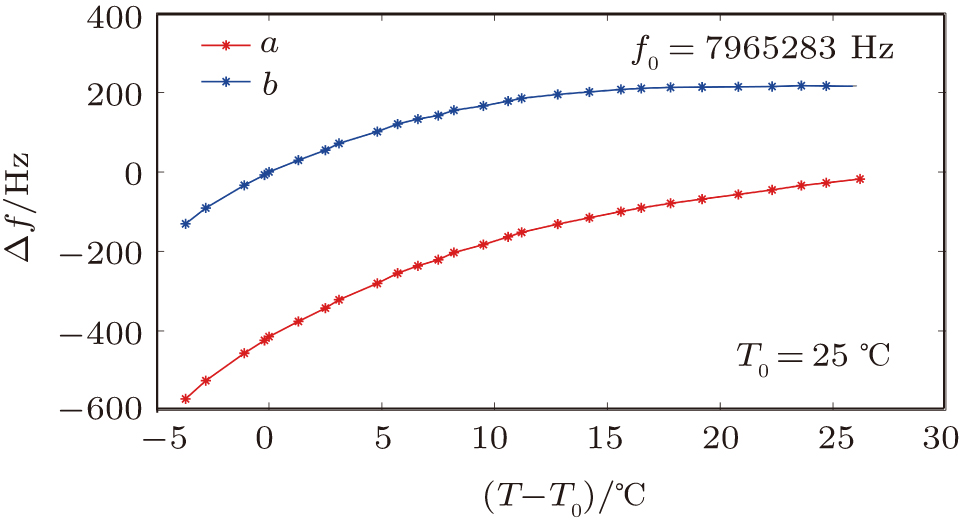 | Fig. 7. (color online) The resonator frequency of QCM in pure water (curve a); The direct temperature effect (
|
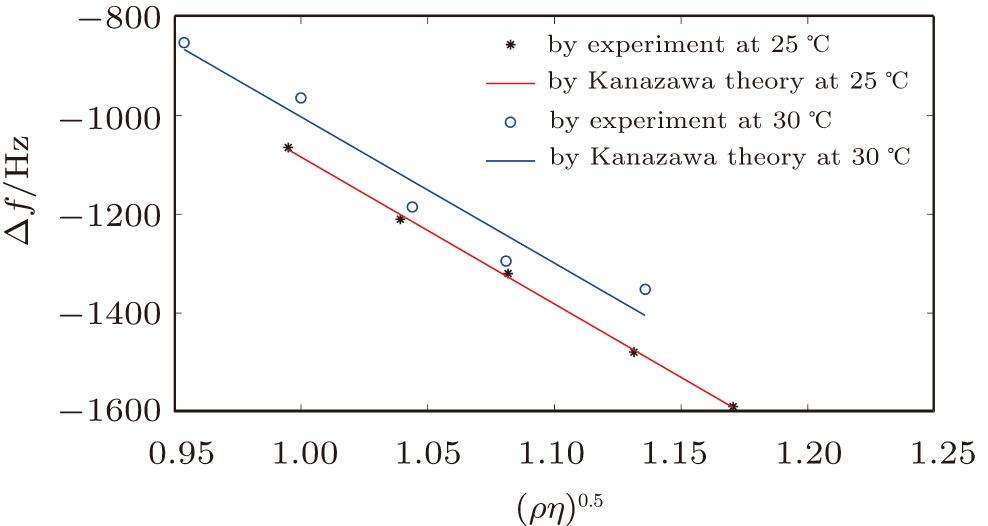
By comparing Eqs. (
Figure
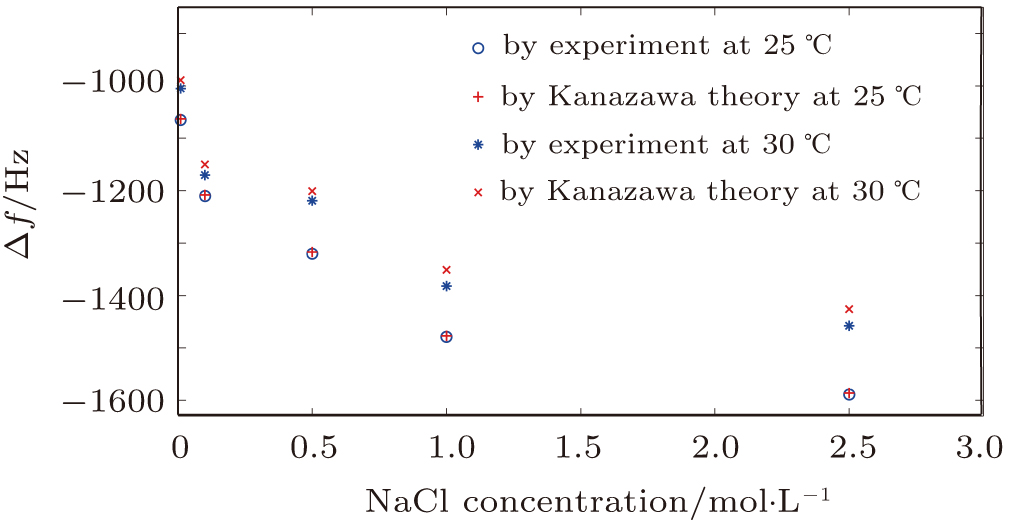 | Fig. 8. (color online) Indirect effect on the QCM resonator in the NaCl solutions with different concentrations. |
At 25 °C, a good agreement was found for 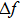
Experiments demonstrated the phenomena of the QCM resonator frequency drift in the aqueous solutions when its temperature ranged from 20 °C to 35 °C. The drift resulting from the hybrid temperature effect which severely affected the performance of the QCM resonator. Thus, the Sauerbrey equation should be further improved for QCM drift compensation to enhance the measurement accuracy at room temperature.
According to Assumption 3, when the QCM measurement is is conducted in aqueous solutions, the frequency change 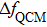
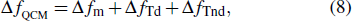 |
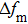
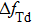
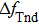
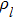

Equation (
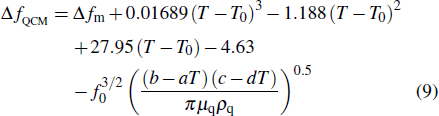 |
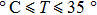
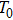
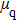
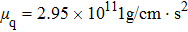
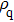
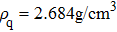
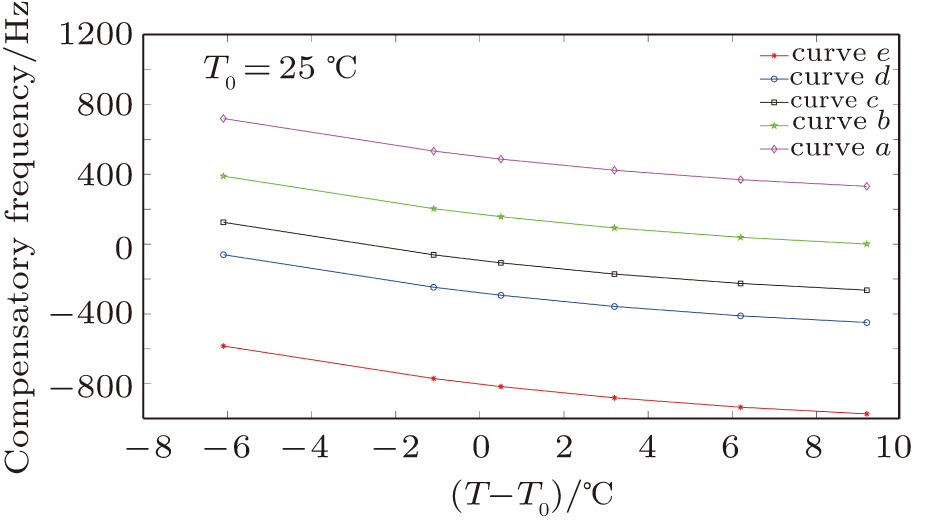
Figure 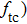
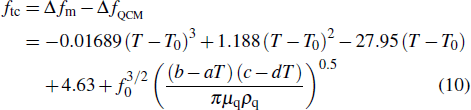 |
The compensatory frequencies were obtained by considering the influences of the direct temperature effect and indirect temperature effect.
According to Eq. (
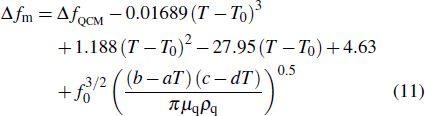 |
We validated Eq. (

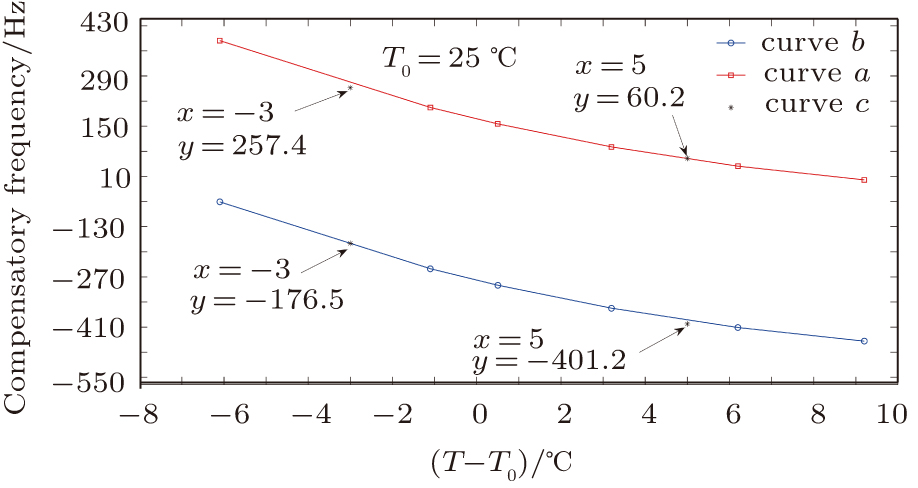 | Fig. 11. (color online) The compensation frequencies of the QCM resonator in NaCl solutions with different concentrations. (a) 0.1 mol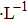
|
Table 
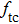
| Table 6.
Statistics of the compensation frequencies of the QCM resonator in NaCl solutions. . |
In this paper, we investigated the hybrid temperature effect on the QCM resonator in aqueous solutions to build a more accurate relationship among the resonator frequency of the QCM resonator, the adsorbed mass, and the environmental temperature. We presented an equation developed from the Sauerbrey equation based on the hybrid temperature effect. The proposed method effectively compensated for the drift of the QCM resonator. It avoided variations in the resonator response due to the environmental temperature variations occurred during the actual measurement. These results will play a significant role in future QCM application at the room temperature.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] |