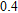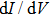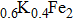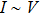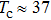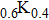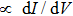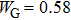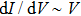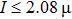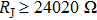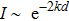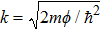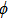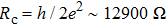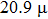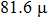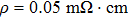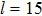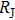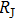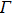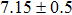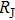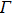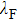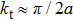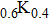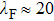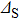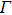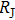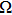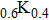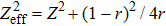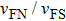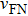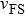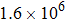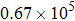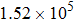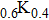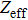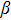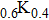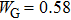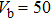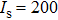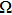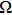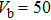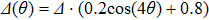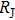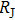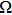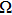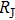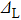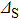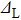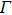1. IntroductionTunneling spectroscopy based on normal metal/superconductor (NS) junctions has been widely used to study the magnitude and symmetry of superconducting gaps.[1,2] Nevertheless, it is often difficult to distinguish a superconducting gap in a tunneling spectrum from other gaps such as band gap and charge-density-wave gap because of their similar appearances. Alternatively, once the barrier of the NS junction becomes lower, a hole could be reflected at the NS interface when an electron injects into the superconductor, which is called Andreev reflection.[3] If the barrier is low enough, Andreev reflection will dominate the spectrum by enhancing or even doubling the conductance within the superconducting gap,[4,5] which is completely different from the behaviors of the other gaps. Thus one can use Andreev reflection to identify superconducting gaps and probe their pairing symmetries[6–8] by fabricating point contacts between normal metals and superconductors. The spectra of
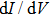 versus V obtained on such a point contact could give important information about the superconducting order parameter, where I is the net current through the contact and V is the applied bias voltage.
versus V obtained on such a point contact could give important information about the superconducting order parameter, where I is the net current through the contact and V is the applied bias voltage.
Typical ways of creating a point contact rely on some mechanical devices (or combined with piezoceramics) to drive a normal metal tip towards a sample to be studied and vice versa.[9–11] These attempts have achieved great successes in the studies of superconductivity.[6,7,12] However, due to the lower positioning accuracy of the devices and possible contaminations of both tips and samples, these methods are difficult to use in precisely controlling the real contact area. In order to apply the point-contact technology to study the strongly inhomogeneous superconductors, such as high-temperature superconductors, the metal tip has to be positioned in a specific area of interest with a size of several nanometers, which can be accomplished by using scanning tunneling microscopy/spectroscopy (STM/STS).[1,13] A scanning tunneling spectroscope can detect electronic inhomogeneity on the atomic scale and then in-situ establish a clean point contact between the STM tip and the selected region on the sample surface. This technique has been used to study metal/metal point contacts,[14–18] while reports on NS point contact created by STM are scarce and only limited to some conventional superconductors.[19–21]
In this paper, we report the transition from the tunneling regime to local point contact on the iron-based superconductor Ba
 As
As
 accomplished by using STM/STS. The entire process evolving from single-particle tunneling to Andreev reflection can be well understood in the framework of BTK theory[4] with reasonable parameters. The spatial resolution of better than 60 Å paves a promising way to study the inhomogeneity in unconventional superconductors.
accomplished by using STM/STS. The entire process evolving from single-particle tunneling to Andreev reflection can be well understood in the framework of BTK theory[4] with reasonable parameters. The spatial resolution of better than 60 Å paves a promising way to study the inhomogeneity in unconventional superconductors.
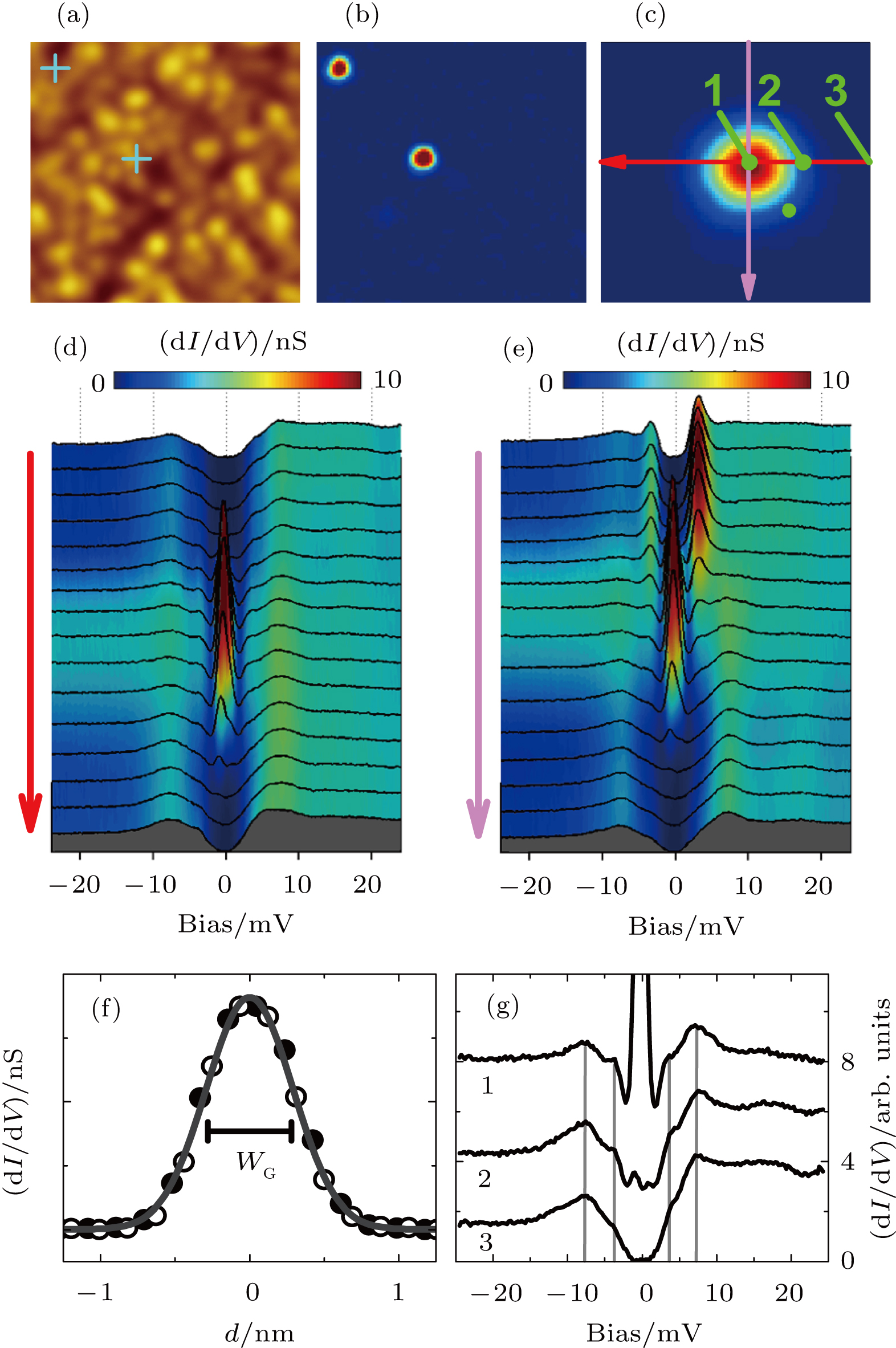
3. Results and discussionFigure 1(a) shows a topographic image of the cleaved surface of Ba
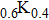 Fe
Fe
 As
As
 . The surface is covered by disordered bright “clusters" inferred to be scattered Ba or K atoms from the broken (Ba,K) layer.[23,24] The image of local density of states (DOS
. The surface is covered by disordered bright “clusters" inferred to be scattered Ba or K atoms from the broken (Ba,K) layer.[23,24] The image of local density of states (DOS
 ) at zero energy was presented in Fig. 1(b) in which two single impurities can be identified due to the DOS peaks as shown in Figs. 1(d) and 1(e), similar to some other iron-based superconductors.[25–27] The locations of the impurities have been marked as two crosses in Fig. 1(a).
) at zero energy was presented in Fig. 1(b) in which two single impurities can be identified due to the DOS peaks as shown in Figs. 1(d) and 1(e), similar to some other iron-based superconductors.[25–27] The locations of the impurities have been marked as two crosses in Fig. 1(a).
It can be seen that the crosses do not overlap any “clusters” mentioned above, indicating that the observed impurities should be situated in the lower layer. The tunneling spectra taken along the orthogonal paths through a single impurity (illustrated in Fig. 1(c) are presented in Figs. 1(d) and 1(e), respectively. When getting close to the impurity center, a low-energy DOS peak emerges and becomes stronger and stronger. As evidenced in Fig. 1(f), the relation between the zero-bias conductance and the distance from the impurity center can be well fitted using the Gauss function with a characteristic width of
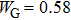 nm, indicating the sensitivity of DOS to the distance from the impurity center. Figure 1(g) shows the spectra taken at some typical positions, namely, the center (No. 1), the edge (No. 2), and the outside (No. 3) of the impurity as labeled in Fig. 1(c). Two superconducting gaps can be identified by the coherence peaks or the kinks inside denoted by the vertical lines. The gap values of 7.5 meV and 3.5 meV are consistent with our previous measurements.[24,28] Clearly identifying a single impurity from a DOS map demonstrates that our STM has enough spatial resolution and stability, which are prerequisites for building a local point contact between an STM tip and a sample.
nm, indicating the sensitivity of DOS to the distance from the impurity center. Figure 1(g) shows the spectra taken at some typical positions, namely, the center (No. 1), the edge (No. 2), and the outside (No. 3) of the impurity as labeled in Fig. 1(c). Two superconducting gaps can be identified by the coherence peaks or the kinks inside denoted by the vertical lines. The gap values of 7.5 meV and 3.5 meV are consistent with our previous measurements.[24,28] Clearly identifying a single impurity from a DOS map demonstrates that our STM has enough spatial resolution and stability, which are prerequisites for building a local point contact between an STM tip and a sample.
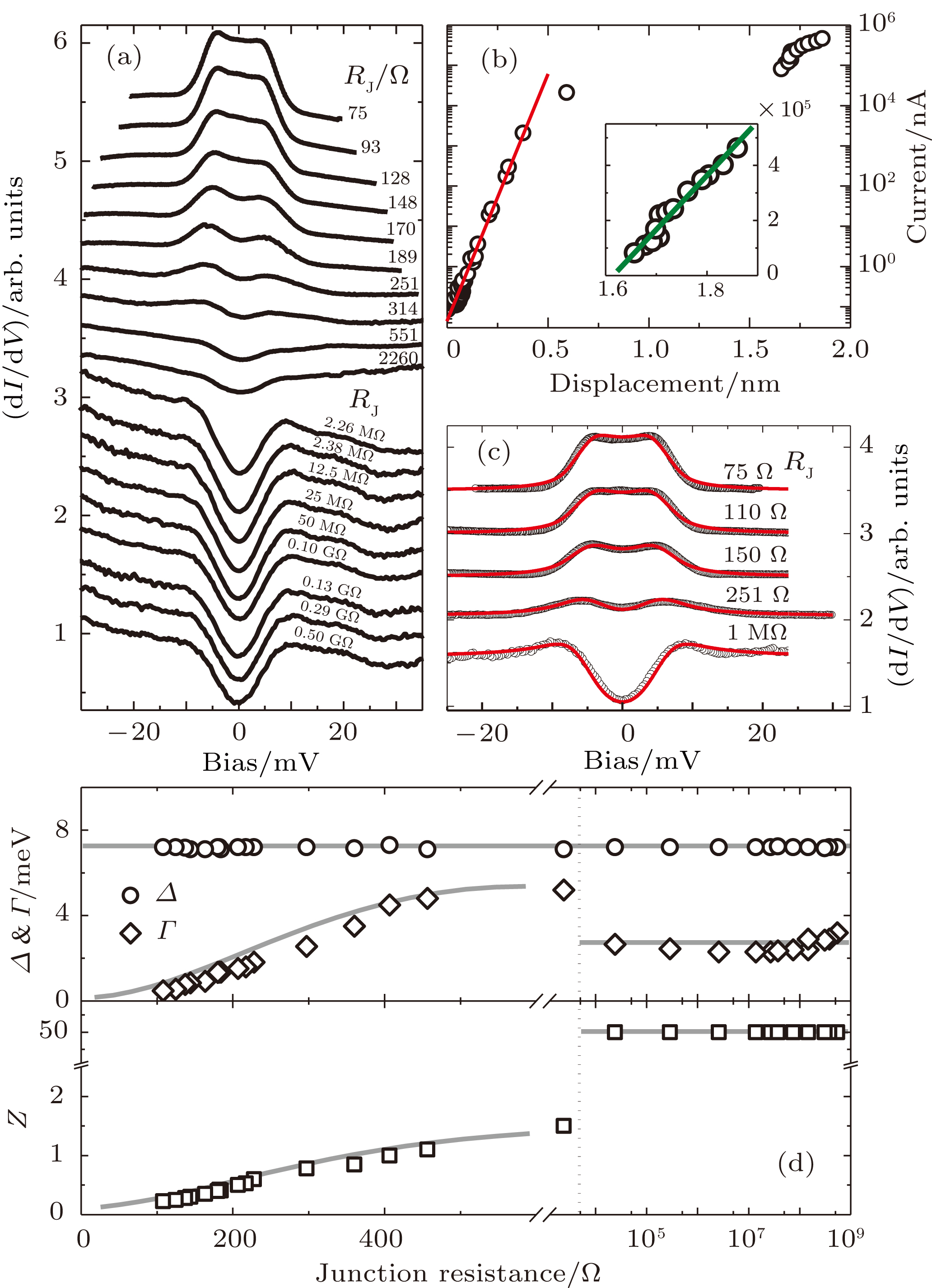
In order to make a clean N/S point contact, we selected a location far away from any impurities. By driving the STM tip towards the sample surface step-by-step and taking
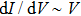 spectrum simultaneously, we obtained a series of spectra with a continuous evolution as presented in Fig. 2(a). The relationship between the measured tunneling current I at a fixed bias voltage and the tip displacement is plotted in Fig. 2(b), in which an exponential dependence can be seen for
spectrum simultaneously, we obtained a series of spectra with a continuous evolution as presented in Fig. 2(a). The relationship between the measured tunneling current I at a fixed bias voltage and the tip displacement is plotted in Fig. 2(b), in which an exponential dependence can be seen for
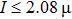 A or junction resistance
A or junction resistance
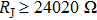 . This is in good agreement with the function of
. This is in good agreement with the function of
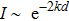 expected in the tunneling regime, where
expected in the tunneling regime, where
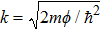 , d is tip–sample distance, and
, d is tip–sample distance, and
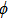 depends on the work functions of the tip and sample. In this regime, the tunneling spectra look very similar for various
depends on the work functions of the tip and sample. In this regime, the tunneling spectra look very similar for various
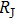 s spanning four orders of magnitude because they are proportional to the DOS at the same position. Here, most of the spectral weight is contributed from the larger superconducting gap.[29]
s spanning four orders of magnitude because they are proportional to the DOS at the same position. Here, most of the spectral weight is contributed from the larger superconducting gap.[29]
It also can be seen from Fig. 2(b) that I versus tip displacement deviates from the exponential law when
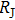 falls just below the single channel Landauer quantum resistance (
falls just below the single channel Landauer quantum resistance (
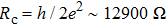 ),[30,31] which is consistent with previous reports on some other materials.[14–18] Such a deviation indicates the formation of point contact and the spectrum changes dramatically due to the collapse of the junction barrier. As noted in Fig. 2(b), a discontinuity appears in the current range of
),[30,31] which is consistent with previous reports on some other materials.[14–18] Such a deviation indicates the formation of point contact and the spectrum changes dramatically due to the collapse of the junction barrier. As noted in Fig. 2(b), a discontinuity appears in the current range of
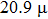 A to
A to
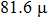 A, corresponding to a tip displacement of about 1 nm. This might arise from the rearrangement of the atoms on the tip apex and/or sample surface.[32,33] As the tip approaches further, I increases almost linearly, as evidenced from the inset of Fig. 2(b). Correspondingly, the spectral weight is contributed more and more from Andreev reflection as shown in Fig. 2(a). In the ballistic regime, the electron mean free path l is much larger than the contact radius a and the electrons can flow through the contact with no scattering. The resistance of such contact was calculated by Sharvin[34] and expressed as
A, corresponding to a tip displacement of about 1 nm. This might arise from the rearrangement of the atoms on the tip apex and/or sample surface.[32,33] As the tip approaches further, I increases almost linearly, as evidenced from the inset of Fig. 2(b). Correspondingly, the spectral weight is contributed more and more from Andreev reflection as shown in Fig. 2(a). In the ballistic regime, the electron mean free path l is much larger than the contact radius a and the electrons can flow through the contact with no scattering. The resistance of such contact was calculated by Sharvin[34] and expressed as
 . Using
. Using
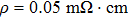 [35] and
[35] and
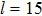 nm[36] from transport measurements, the maximal contact radius corresponding to the lowest
nm[36] from transport measurements, the maximal contact radius corresponding to the lowest
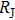 of
of
 can be estimated to be
can be estimated to be
 Å, much smaller than the mean free path l. A higher
Å, much smaller than the mean free path l. A higher
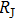 value will give a smaller contact radius, thus ensuring the ballistic regime in our measurements all the while. All the spectra from tunneling regime to point contact regime obtained here can be fitted pretty well by using a modified BTK model[4,37,38] in which an anisotropic gap is adopted.[24] Some examples of such fittings are given in Fig. 2(c) and all the fitting parameters are plotted in Fig. 2(d), where Z is effective barrier, Δ is superconducting gap, and
value will give a smaller contact radius, thus ensuring the ballistic regime in our measurements all the while. All the spectra from tunneling regime to point contact regime obtained here can be fitted pretty well by using a modified BTK model[4,37,38] in which an anisotropic gap is adopted.[24] Some examples of such fittings are given in Fig. 2(c) and all the fitting parameters are plotted in Fig. 2(d), where Z is effective barrier, Δ is superconducting gap, and
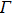 is broadening factor.
is broadening factor.
For all these fittings, gap parameter Δ keeps constant (
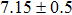 meV). Barrier Z stays at 50 (infinite barrier) for the tunneling regime while it decreases continuously with reducing
meV). Barrier Z stays at 50 (infinite barrier) for the tunneling regime while it decreases continuously with reducing
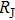 in the point contact regime. The good consistency between the theoretical model and our experimental data indicates the successful realization of the transition from tunneling regime to local point contact in Ba
in the point contact regime. The good consistency between the theoretical model and our experimental data indicates the successful realization of the transition from tunneling regime to local point contact in Ba
 Fe
Fe
 As
As
 with a spatial resolution of several nanometers. Interestingly, the broadening parameter
with a spatial resolution of several nanometers. Interestingly, the broadening parameter
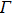 undergoes a sudden increase when tip–sample contacting occurs, then decreases gradually as the junction resistance diminishes in the PC regime, consistent with previous observations.[39,40] Since the PCs were established in a non-contaminated environment, this broadening effect can be explained by the coupling of electrons and two level fluctuators (TLF’s).[32] In this work, a TLF may be developed by the fluctuations between two different configurations of the tip apex and/or the location on the sample surface in contact with the tip. Such spectral broadening induced by the rearrangement of a group of atoms has been observed in ballistic PCs between Ag and Nb.[33] Nevertheless, in our case, quantum confinement effect should also be taken into account in addition to the electron-TLF coupling, since the contact area can be extremely small and comparable to the Fermi wave length
undergoes a sudden increase when tip–sample contacting occurs, then decreases gradually as the junction resistance diminishes in the PC regime, consistent with previous observations.[39,40] Since the PCs were established in a non-contaminated environment, this broadening effect can be explained by the coupling of electrons and two level fluctuators (TLF’s).[32] In this work, a TLF may be developed by the fluctuations between two different configurations of the tip apex and/or the location on the sample surface in contact with the tip. Such spectral broadening induced by the rearrangement of a group of atoms has been observed in ballistic PCs between Ag and Nb.[33] Nevertheless, in our case, quantum confinement effect should also be taken into account in addition to the electron-TLF coupling, since the contact area can be extremely small and comparable to the Fermi wave length
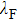 of the sample.[41,42] In this case, the confinement in the lateral direction on a scale of 2a gives a lower boundary of the transverse momentum
of the sample.[41,42] In this case, the confinement in the lateral direction on a scale of 2a gives a lower boundary of the transverse momentum
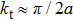 , which will reduce the probability of the electrons propagating through the contact.[42] By using the Fermi velocity and electron effective mass of Ba
, which will reduce the probability of the electrons propagating through the contact.[42] By using the Fermi velocity and electron effective mass of Ba
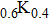 Fe
Fe
 As
As
 measured by ARPES,[43] we can estimate the Fermi wavelengths of the sample as
measured by ARPES,[43] we can estimate the Fermi wavelengths of the sample as
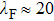 –115 Å for all Fermi surfaces, which are indeed comparable to the contact dimension for various resistances.
–115 Å for all Fermi surfaces, which are indeed comparable to the contact dimension for various resistances.
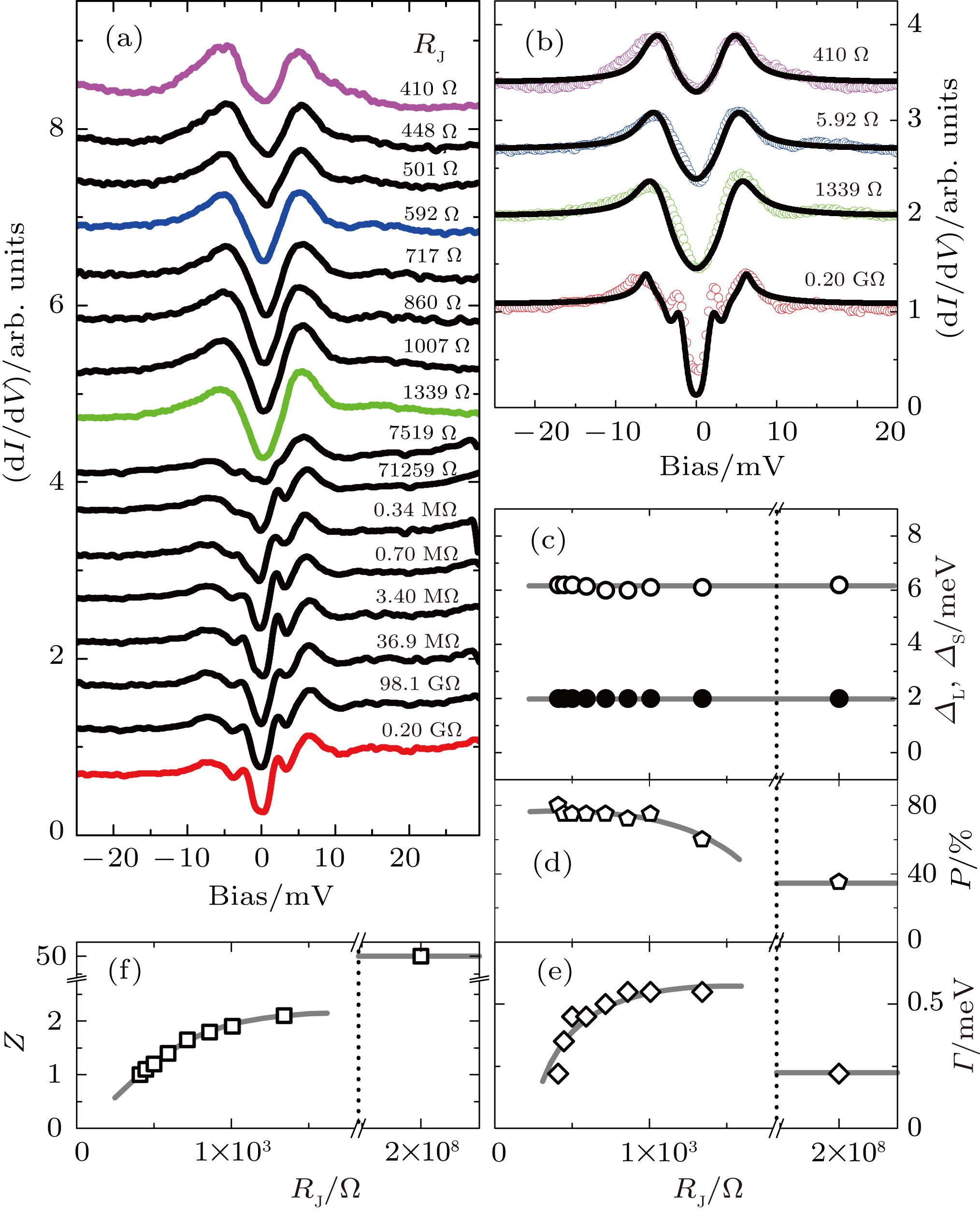
In order to prove the tip’s stability, we repeated the measurements on another location with a spectral shape different from that shown in Fig. 2. The spectra recorded in the approaching process are presented in Fig. 3(a). In this case, both superconducting gaps contribute a lot to the spectra[24,44] and hence a two-gap BTK model was adopted to fit the data. Some of these fits are illustrated in Fig. 3(b) and all fitting parameters are given in Figs. 3(c)– 3(f). Both the larger gap
 and the smaller one
and the smaller one
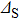 are almost constant, meanwhile, Z and
are almost constant, meanwhile, Z and
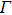 have similar behaviors to that shown in Fig. 2(d), demonstrating a continuous transition from tunneling regime to local point contact. The lowest
have similar behaviors to that shown in Fig. 2(d), demonstrating a continuous transition from tunneling regime to local point contact. The lowest
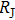 obtained here is 410
obtained here is 410
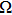 corresponding to a maximal contact diameter of 56 Å (a = 28 Å) allowing us to determine the superconducting order parameter with a spatial resolution better than 56 Å.
corresponding to a maximal contact diameter of 56 Å (a = 28 Å) allowing us to determine the superconducting order parameter with a spatial resolution better than 56 Å.
It is noted that the spectral weight contributed from the larger gap (P) is 35% in tunneling regime and changes up to 75% after tip–sample contacting. This remarkable change reflects the different features of various Fermi pockets in Ba
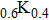 Fe
Fe
 As
As
 . For a point contact formed between two metals, the effective barrier of the contact can be expressed by
. For a point contact formed between two metals, the effective barrier of the contact can be expressed by
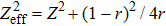 , where Z is the true barrier while the other part is contributed from the Fermi surface mismatch between the two metals. In our case, r equals to
, where Z is the true barrier while the other part is contributed from the Fermi surface mismatch between the two metals. In our case, r equals to
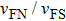 in which
in which
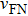 and
and
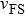 are the Fermi velocities of the normal metal tip and the studied superconductor, respectively. By taking the Fermi velocities of
are the Fermi velocities of the normal metal tip and the studied superconductor, respectively. By taking the Fermi velocities of
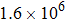 m/s for the STM tip and
m/s for the STM tip and
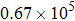 m/s–
m/s–
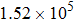 m/s for Ba
m/s for Ba
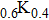 Fe
Fe
 As
As
 ,[43] we can obtain the
,[43] we can obtain the
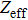 values of 2.35 for the Fermi pocket having a smaller superconducting gap and of 1.47–1.91 for the Fermi pockets having larger gaps. That is to say, when point contact is formed, the electrons on the band with a smaller gap will experience a much higher barrier than that from the bands with larger gaps. This is the reason why the spectral weight contributed from the larger gap increases significantly after tip–sample contacting. Electrons with smaller Fermi velocities have to surmount larger barrier to go through the junction. Hence, contribution from
values of 2.35 for the Fermi pocket having a smaller superconducting gap and of 1.47–1.91 for the Fermi pockets having larger gaps. That is to say, when point contact is formed, the electrons on the band with a smaller gap will experience a much higher barrier than that from the bands with larger gaps. This is the reason why the spectral weight contributed from the larger gap increases significantly after tip–sample contacting. Electrons with smaller Fermi velocities have to surmount larger barrier to go through the junction. Hence, contribution from
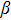 band is suppressed relatively due to its small Fermi velocity.[43]
band is suppressed relatively due to its small Fermi velocity.[43]