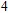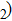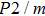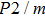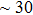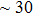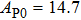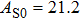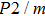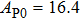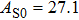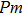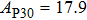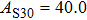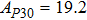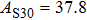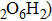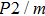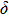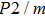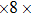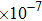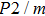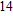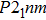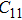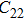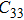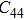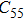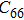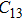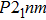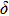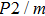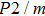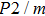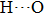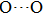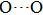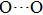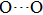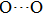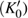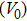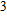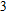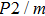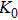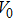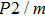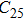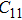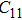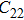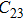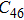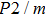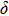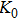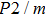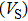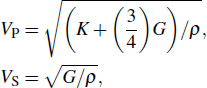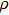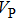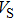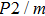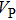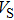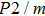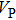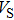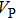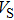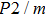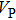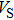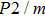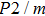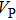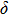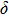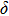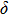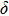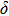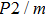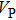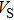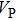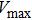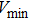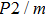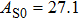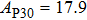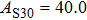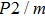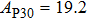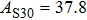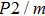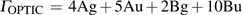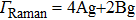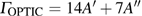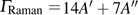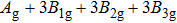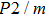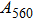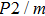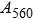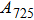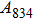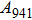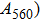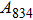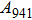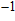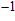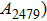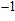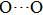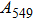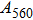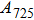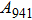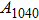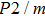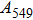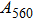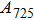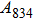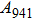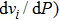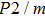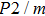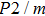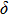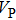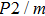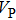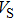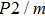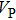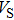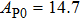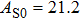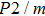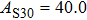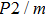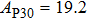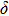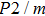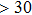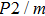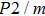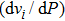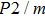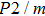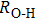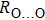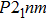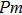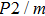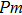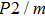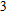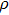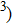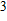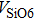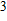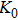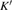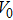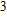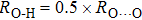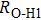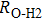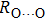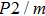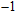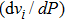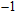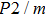1. IntroductionThe presence of water in the lower mantle has various functions, such as dramatically lowering the melting temperature of mantle rocks, causing arc magmatism, reducing the magma viscosity and density, enhancing magma migration, influencing the elastic and rheological properties of the mantle, and broadening seismic discontinuities.[1] It is now accepted that water can percolate through the Earth’s interior by subducting slabs through hydrous minerals, such as serpentine.[2,3] The serpentine can transform into several dense hydrous magnesium silicates (DHMSs), depending on the pressure and temperature conditions.[4–6] Since the first discovery of 10-Å phase,[7] dense hydrous magnesium silicates including 3.65-Å phase, phase A, phase B, superhydrous phase B, phase D, phase E, etc. have received considerable attention because of their presumed role in the water resources of the Earth.[8–10]
Phase D (MgSi
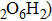 has been considered to be the most thermodynamically stable phase under lower mantle conditions.[11,12] It has been discovered that phase D transforms into the phase H at 44 GPa.[13] Phase H was first announced to be stable up to 52 GPa and had a crystal structure similar to that of CaCl
has been considered to be the most thermodynamically stable phase under lower mantle conditions.[11,12] It has been discovered that phase D transforms into the phase H at 44 GPa.[13] Phase H was first announced to be stable up to 52 GPa and had a crystal structure similar to that of CaCl
 -type SiO
-type SiO
 , of which half of the Si atoms replace Mg atoms and hydrogen atoms are located at the edges of the vacant octahedral sites (Fig. 1). Early theoretical studies predicted the crystal structure of phase H to be monoclinic with
, of which half of the Si atoms replace Mg atoms and hydrogen atoms are located at the edges of the vacant octahedral sites (Fig. 1). Early theoretical studies predicted the crystal structure of phase H to be monoclinic with
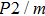 symmetry.[14] Since then, phase H has been discussed to evaluate its structural stability, elastic properties and the possibility of forming a solid solution with
symmetry.[14] Since then, phase H has been discussed to evaluate its structural stability, elastic properties and the possibility of forming a solid solution with
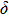 -AlOOH in the lower mantle condition.[14–16] Yet, due to the fact that different analytical methods are adopted, the results of previous studies are controversial. Possible structure of phase H suggested by Bindi et al.[15] was based on energy-dispersive x-ray diffraction while that by Nishi et al.[16] was based on in situ single-crystal x-ray diffraction. Besides, the quality of diffraction data was not accurate enough to determine the positions of hydrogen atoms. On the other hand, the work provided by first principles calculations could not take the thermal vibration effect into consideration.[17] As a result, the structure parameters and symmetry of phase H are discrepant in different studies.
-AlOOH in the lower mantle condition.[14–16] Yet, due to the fact that different analytical methods are adopted, the results of previous studies are controversial. Possible structure of phase H suggested by Bindi et al.[15] was based on energy-dispersive x-ray diffraction while that by Nishi et al.[16] was based on in situ single-crystal x-ray diffraction. Besides, the quality of diffraction data was not accurate enough to determine the positions of hydrogen atoms. On the other hand, the work provided by first principles calculations could not take the thermal vibration effect into consideration.[17] As a result, the structure parameters and symmetry of phase H are discrepant in different studies.
In this study, in order to further understand the stability of phase H under high pressure, the crystal structure, elastic constants, seismic velocities and anisotropies of the two different possible symmetry phase H’s (Pm and
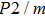 symmetry) are calculated by using first-principles simulations. The
symmetry) are calculated by using first-principles simulations. The
 symmetry is based on the fully optimized structure by Tsuchiya and Mookherjee[17] while Pm symmetry possesses hydrogen atoms drawn at the Wyckoff position, which is inspired by previous single-crystal x-ray diffraction research.[16] Raman vibrational properties are also analyzed to evaluate the changes of the crystal structure with pressure.
symmetry is based on the fully optimized structure by Tsuchiya and Mookherjee[17] while Pm symmetry possesses hydrogen atoms drawn at the Wyckoff position, which is inspired by previous single-crystal x-ray diffraction research.[16] Raman vibrational properties are also analyzed to evaluate the changes of the crystal structure with pressure.
2. Methods2.2. Benchmark calculationsTo assess the performances of the DFT and DFPT total-energy approach in our study, test calculations of the cell parameters and elastic constants of phase H were performed. The differences in cell volumes, lengths of a, b, and c axes between the calculated results and corresponding experimental values[16] are 0.1%, 1.2%, 0.7%, and 0.4% respectively, or 2.7%, 1.7%, 0.6%, and 0.7% compared with the other experimental results[15] (Table 1). Comparing our calculated results with the calculated results of Tsuchiya,[14] the tiny differences can be ignored. Since no experimental results of elastic constants are available, the calculated values of elastic constants[17] are adopted for comparison. The differences in
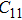 ,
,
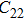 ,
,
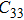 ,
,
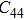 ,
,
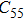 ,
,
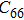 ,
,
 , and
, and
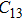 between this work and previous study are 2.2%, 5.4%, 2.9%, 6.6%, 3.2%, 10.4%, 2.8%, and 6.7% at 30 GPa, respectively. Notably, the pseudopotential of magnesium in former research[17] is generated by the method of von Barth and Car. In contrast, here we adopted norm-conserving pseudopotentials for all atoms, which may lead to the discrepancies in elastic constants. Such close agreement between the experimental and calculated values of lattice parameters and elastic constants demonstrates the validity of this computational project.
between this work and previous study are 2.2%, 5.4%, 2.9%, 6.6%, 3.2%, 10.4%, 2.8%, and 6.7% at 30 GPa, respectively. Notably, the pseudopotential of magnesium in former research[17] is generated by the method of von Barth and Car. In contrast, here we adopted norm-conserving pseudopotentials for all atoms, which may lead to the discrepancies in elastic constants. Such close agreement between the experimental and calculated values of lattice parameters and elastic constants demonstrates the validity of this computational project.
Table 1.
Table 1.
 | Table 1.
Benchmark calculations results.
. |
3. Results3.1. Crystal structureEver since the first-principles prediction of this new mineral was proposed,[14] phase H has been observed in the two separate experimental research studies.[15,16] However, due to the difficulties in detecting the positions of hydrogen atoms and pressure-induced rapid amorphization of the sample,[15,16] the structure of phase H was roughly judged to be an orthorhombic system with symmetry
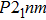 (
(
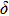 -AlOOH-type structure) and orthorhombic system with symmetry Pnnm (CaCl
-AlOOH-type structure) and orthorhombic system with symmetry Pnnm (CaCl
 type structure), respectively. However, theoretical studies proposed different crystal structures: monoclinic structures with Pm and
type structure), respectively. However, theoretical studies proposed different crystal structures: monoclinic structures with Pm and
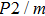 symmetry, which have been proved to be more thermodynamically stable than the experimental ones. The major difference between the theoretical and experimental structures is the arrangement of Mg and Si atoms. Both experimental structures possess disordered distributions of cations (Mg, Si), while theoretical structures possess ordered distributions of Mg and Si in octahedral sites. Furthermore, the
symmetry, which have been proved to be more thermodynamically stable than the experimental ones. The major difference between the theoretical and experimental structures is the arrangement of Mg and Si atoms. Both experimental structures possess disordered distributions of cations (Mg, Si), while theoretical structures possess ordered distributions of Mg and Si in octahedral sites. Furthermore, the
 symmetry possesses symmetric hydrogen bonds, while the Pm symmetry possesses asymmetric hydrogen bonds. The Pm and
symmetry possesses symmetric hydrogen bonds, while the Pm symmetry possesses asymmetric hydrogen bonds. The Pm and
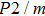 symmetries slightly deviate from experiential structures and were provided to be precise enough for the simulation of phase H.[17] Therefore, we select the two structures from theoretical studies as our investigation objects.[14]
symmetries slightly deviate from experiential structures and were provided to be precise enough for the simulation of phase H.[17] Therefore, we select the two structures from theoretical studies as our investigation objects.[14]
Geometry optimization has been conducted on both Pm and
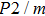 structures from 0 GPa to 100 GPa. The detailed cell parameters of the two structures are listed in Table 2 and Supplement Tables A1, A2, and A3 in Appendix A. Figure 2 shows the pressure-lattice parameters of the two structures under high pressures. The lengths of a, b, and c axes decrease at almost the same ratio with increasing pressure, at the same time the
structures from 0 GPa to 100 GPa. The detailed cell parameters of the two structures are listed in Table 2 and Supplement Tables A1, A2, and A3 in Appendix A. Figure 2 shows the pressure-lattice parameters of the two structures under high pressures. The lengths of a, b, and c axes decrease at almost the same ratio with increasing pressure, at the same time the
 angle decreases to 90
angle decreases to 90
 . Two-stage changes of lattice parameters of the two structures with increasing pressure are observed. The variation tendencies for lattice parameters of the two structures approach each other from 0 GPa to 30 GPa, above which the two structures almost keep the same lattice parameters. A possible explanation to this result is the symmetrization of hydrogen bonds. Since the first prediction of symmetrization of the hydrogen bonds in ice VII,[33] a large number of research studies have been conducted to understand the pressure dependence of hydrogen bonds’ symmetrization.[34–36] It is widely accepted that the bonded O–H distance shows relevance to the
. Two-stage changes of lattice parameters of the two structures with increasing pressure are observed. The variation tendencies for lattice parameters of the two structures approach each other from 0 GPa to 30 GPa, above which the two structures almost keep the same lattice parameters. A possible explanation to this result is the symmetrization of hydrogen bonds. Since the first prediction of symmetrization of the hydrogen bonds in ice VII,[33] a large number of research studies have been conducted to understand the pressure dependence of hydrogen bonds’ symmetrization.[34–36] It is widely accepted that the bonded O–H distance shows relevance to the
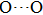 distance in many O–
distance in many O–
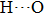 geometry systems. In a weak hydrogen bond system with phase H, where
geometry systems. In a weak hydrogen bond system with phase H, where
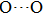 distance is more than 2.6 Å, the hydrogen bond length is almost fixed at 1 Å. Once the
distance is more than 2.6 Å, the hydrogen bond length is almost fixed at 1 Å. Once the
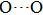 bond is under high pressure, the
bond is under high pressure, the
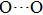 distance would decrease to around 2.4 Å and the O–H length could increase to the half of the
distance would decrease to around 2.4 Å and the O–H length could increase to the half of the
 distance, where the hydrogen is located in the middle of two oxygen atoms. The hydrogen bonds of phase H with Pm symmetry become symmetrized at pressures higher than 30 GPa (Fig. 2). When the
distance, where the hydrogen is located in the middle of two oxygen atoms. The hydrogen bonds of phase H with Pm symmetry become symmetrized at pressures higher than 30 GPa (Fig. 2). When the
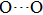 distance reduces with pressure increasing from 0 GPa to 30 GPa, the length of O–H bond also increases rather than falls. The length of O–H is kept at half of the distance of
distance reduces with pressure increasing from 0 GPa to 30 GPa, the length of O–H bond also increases rather than falls. The length of O–H is kept at half of the distance of
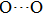 under higher pressures, which means that the hydrogen atom is located in the middle of the pair of oxygen atoms. This result indicates that phase H would turn from Pm structure with asymmetric hydrogen bonds into the
under higher pressures, which means that the hydrogen atom is located in the middle of the pair of oxygen atoms. This result indicates that phase H would turn from Pm structure with asymmetric hydrogen bonds into the
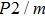 structure with symmetric hydrogen bonds at about 30 GPa. It is also the reason that the two structures with different initial lattice parameters can become the same at pressures higher than 30 GPa.
structure with symmetric hydrogen bonds at about 30 GPa. It is also the reason that the two structures with different initial lattice parameters can become the same at pressures higher than 30 GPa.
Table 2.
Table 2.
 | Table 2.
Structural properties of phase H.
. |
The volume–pressure relationships (Fig. 2) for the two structures of phase H are well described by the finite strain formulation of the third order Birch–Murnaghan.[37] Values of bulk moduli
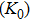 are 156.2 GPa and 177.9 GPa, values of the pressure derivative of the zero pressure bulk modulus
are 156.2 GPa and 177.9 GPa, values of the pressure derivative of the zero pressure bulk modulus
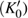 ) are 4.40 and 4.18 and the values of initial unit-cell volume
) are 4.40 and 4.18 and the values of initial unit-cell volume
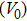 are 59.3 {\AA
are 59.3 {\AA
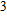 } and 58.4 Å
} and 58.4 Å
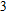 for Pm and
for Pm and
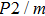 structures, respectively. The differences in initial unit-cell volume,
structures, respectively. The differences in initial unit-cell volume,
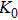 and
and
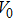 , between the results in this work (Pm) and previous calculation results (
, between the results in this work (Pm) and previous calculation results (
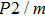 )[17] are 2.9%, 5.9%, and 1.6%, respectively.
)[17] are 2.9%, 5.9%, and 1.6%, respectively.
3.2. ElasticityThe pressure-dependent elastic constants for the two phase H are shown in Fig. 3 and Supplement Table A3. All elastic constants, except for
 and
and
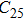 both of which maintain around 0 GPa, increase with pressure rising, which is different from the previous result.[17] We think that the discrepancy of pseudopotential selected for magnesium might result in the differences in lattice parameters. The differences in lattice parameters in turn result in the discrepancies in elastic constants. For instance, the values of lattice parameter a in this work and the previous work[17] have a difference of 0.40% under 30 GPa, and this leads to a difference of 0.58% in elastic constant
both of which maintain around 0 GPa, increase with pressure rising, which is different from the previous result.[17] We think that the discrepancy of pseudopotential selected for magnesium might result in the differences in lattice parameters. The differences in lattice parameters in turn result in the discrepancies in elastic constants. For instance, the values of lattice parameter a in this work and the previous work[17] have a difference of 0.40% under 30 GPa, and this leads to a difference of 0.58% in elastic constant
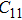 . The principle elastic constants
. The principle elastic constants
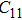 and
and
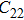 , the shear elastic constant
, the shear elastic constant
 , and the off-diagonal elastic constants
, and the off-diagonal elastic constants
 ,
,
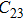 , and
, and
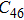 for Pm symmetry are significantly smaller than those of the
for Pm symmetry are significantly smaller than those of the
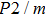 symmetry under low pressures. These constants also sharply rise from 25 GPa to 30 GPa, which is also the pressure range of symmetrization of hydrogen bonds. These results indicate that the elastic constants of Pm symmetry are obviously dependent on the strength of the hydrogen bond. Namely, the symmetrization of hydrogen bonds increases the stiffness of phase H in the direction perpendicular to the c axis direction. Similar anomalous phenomena have been reported in phase D and
symmetry under low pressures. These constants also sharply rise from 25 GPa to 30 GPa, which is also the pressure range of symmetrization of hydrogen bonds. These results indicate that the elastic constants of Pm symmetry are obviously dependent on the strength of the hydrogen bond. Namely, the symmetrization of hydrogen bonds increases the stiffness of phase H in the direction perpendicular to the c axis direction. Similar anomalous phenomena have been reported in phase D and
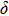 -AlOOH.[35,36] Above 30 GPa, elastic constants for the two structures become equal to each other.
-AlOOH.[35,36] Above 30 GPa, elastic constants for the two structures become equal to each other.
Bulk (K) and shear (G) moduli are determined by the Voigt–Reuss–Hill average (Fig. 4). The bulk and shear moduli of phase H with Pm symmetry show anomalous increases at 25 GPa–30 GPa. The anomalous pressure-dependent bulk and shear moduli are also related to the symmetrization of hydrogen bonds. The bulk modulus
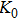 of phase H with Pm symmetry is about 27% smaller than that of
of phase H with Pm symmetry is about 27% smaller than that of
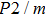 symmetry. Under higher pressures (
symmetry. Under higher pressures (
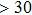 GPa) the bulk and shear moduli of these two structures are almost the same.
GPa) the bulk and shear moduli of these two structures are almost the same.
Sound wave velocities from seismic observation can reflect the composition and structure of the mantle. For crystalline material, the compressional wave velocity
 and shear wave velocity
and shear wave velocity
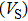 are related to the bulk and shear moduli via
are related to the bulk and shear moduli via
where
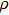
is the mass density determined by the equilibrium of crystal lattice from the first-principles optimization,
K is the bulk modulus, and
G is the shear modulus. The
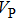
and
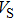
of phase H with
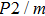
symmetry increase smoothly with increasing pressure. The
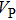
and
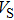
of
Pm symmetry sharply increase from 25 GPa to 30 GPa (Fig.
4) compared with those of
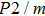
. The pressure dependent
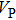
and
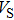
of phase H with
Pm and

symmetry show similar tendencies to those of
K and
G. At pressures above 30 GPa, the values of
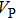
and
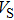
of
Pm and
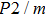
symmetry are almost identical. The symmetrization of hydrogen bonds also generally takes place in plenty of minerals under high pressures, such as ice,

-AlOOH and hydrous silica.
[36,38] Therefore, the symmetrization of hydrogen bonds in dense hydrous silicate may contribute to the abnormally pressure-dependent
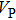
and
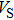
in the upper mantle. The
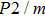
symmetry shows higher density and velocity than the
Pm symmetry under pressure lower than 30 GPa. The transition from
Pm to
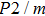
may somewhat contribute to the leaps of density and seismic wave velocity in the transition layer of the mantle.
The values of density,
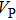 and
and
 of phase D, H, and
of phase D, H, and
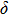 -AlOOH under high pressures are plotted in Fig. 5. Phase D shows the minimal density and velocities while
-AlOOH under high pressures are plotted in Fig. 5. Phase D shows the minimal density and velocities while
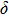 -AlOOH possesses the maximal density and velocities in the hull depth range. It has been proved that phase D would transform into phase H at pressures ranging from about 40 GPa to 50 GPa, and phase H is inclined to form solid solutions with
-AlOOH possesses the maximal density and velocities in the hull depth range. It has been proved that phase D would transform into phase H at pressures ranging from about 40 GPa to 50 GPa, and phase H is inclined to form solid solutions with
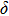 -AlOOH while
-AlOOH while
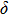 -AlOOH and H show similar structures.[15,16,39] The transformation process from phase D to phase H and finally to solid solution of phase H and
-AlOOH and H show similar structures.[15,16,39] The transformation process from phase D to phase H and finally to solid solution of phase H and
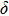 -AlOOH results in the increasing of density and velocities, which show the consistent trends with PREM and AK135 patterns.
-AlOOH results in the increasing of density and velocities, which show the consistent trends with PREM and AK135 patterns.
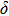 -AlOOH is believed to be stable under lower mantle condition. The forming of solid solution with phase H implicates that the water may have an opportunity to be carried to the lower region of the mantle and even the border of the mantle and core of the Earth. Ultimately, water should be released freely after the solid solution of
-AlOOH is believed to be stable under lower mantle condition. The forming of solid solution with phase H implicates that the water may have an opportunity to be carried to the lower region of the mantle and even the border of the mantle and core of the Earth. Ultimately, water should be released freely after the solid solution of
 -AlOOH and phase H have been heated up by the core, which may contribute to the phenomena of ultralow-velocity regions[40] and large low-shear-velocity provinces[41] detected in the underpart of the mantle.
-AlOOH and phase H have been heated up by the core, which may contribute to the phenomena of ultralow-velocity regions[40] and large low-shear-velocity provinces[41] detected in the underpart of the mantle.
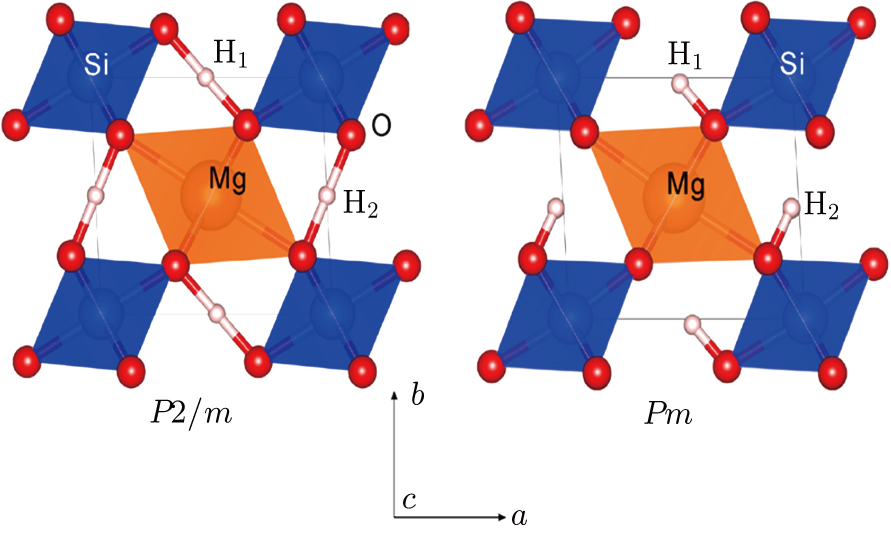
Single crystal seismic velocities for phase H are also calculated by solving Cristoffel’s equation:[42]
 , where n,
, where n,
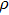 , V, and
, V, and
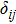 are the propagation direction, density, elastic wave velocity, and Kronecker delta, respectively. Longitudinally and two orthogonally polarized shear wave velocities of the Pm and
are the propagation direction, density, elastic wave velocity, and Kronecker delta, respectively. Longitudinally and two orthogonally polarized shear wave velocities of the Pm and
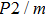 structure at 0, 30, and 60 GPa are shown in Fig. 6 by using the MSAT codes.[43] At 0 GPa, both
structure at 0, 30, and 60 GPa are shown in Fig. 6 by using the MSAT codes.[43] At 0 GPa, both
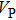 and
and
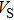 of Pm structure (solid lines) are significantly smaller than those of
of Pm structure (solid lines) are significantly smaller than those of
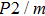 structure (dashed lines) except for those in the [001] direction, since there are only octahedrons of Si and O but no hydrogen bonds parallel to [001] direction. With the symmetrization of hydrogen bonds at 30 GPa, the patterns of single crystal seismic velocities for the two structures become similar. As pressure increases, the difference in anisotropy of seismic velocity between the two structures decreases significantly. The anisotropic properties of phase H at 30 GPa and 60 GPa are almost the same, so the primary reason why the anisotropy changes is crystal structural rearrangement (symmetrization of hydrogen bonds). The maximal
structure (dashed lines) except for those in the [001] direction, since there are only octahedrons of Si and O but no hydrogen bonds parallel to [001] direction. With the symmetrization of hydrogen bonds at 30 GPa, the patterns of single crystal seismic velocities for the two structures become similar. As pressure increases, the difference in anisotropy of seismic velocity between the two structures decreases significantly. The anisotropic properties of phase H at 30 GPa and 60 GPa are almost the same, so the primary reason why the anisotropy changes is crystal structural rearrangement (symmetrization of hydrogen bonds). The maximal
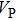 direction for phase H is [101] and the minimal direction is [110]. Azimuthal anisotropy for P and S waves is defined as
direction for phase H is [101] and the minimal direction is [110]. Azimuthal anisotropy for P and S waves is defined as
 , where
, where
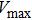 and
and
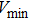 are the maximal and minimal velocity, respectively. The azimuthal anisotropies for phase H are
are the maximal and minimal velocity, respectively. The azimuthal anisotropies for phase H are
 %,
%,
 % (
% (
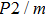 symmetry) and
symmetry) and
 %,
%,
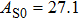 % (Pm symmetry) at 0 GPa, and increase to
% (Pm symmetry) at 0 GPa, and increase to
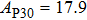 %,
%,
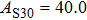 % (
% (
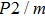 symmetry) and
symmetry) and
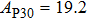 %,
%,
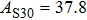 % (Pm symmetry) at 30 GPa. Those results show that the phase H can be a significant source of anisotropy in the lower mantle.
% (Pm symmetry) at 30 GPa. Those results show that the phase H can be a significant source of anisotropy in the lower mantle.
3.3. VibrationVibrational spectra of crystalline solids can be interpreted by using the factor group analysis.[44] For phase H with
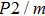 symmetry, the irreducible representation of optical vibrations is
symmetry, the irreducible representation of optical vibrations is
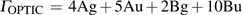 . Since the structure is centro-symmetric, IR and Raman-active modes are mutually exclusive.[45] The Raman-active modes are
. Since the structure is centro-symmetric, IR and Raman-active modes are mutually exclusive.[45] The Raman-active modes are
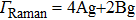 . As for Pm structure, the optical vibration mode is
. As for Pm structure, the optical vibration mode is
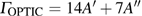 and Raman-active mode is
and Raman-active mode is
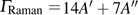 . The Raman-active modes for experimental results (Pnnm and P21nm) are 3
. The Raman-active modes for experimental results (Pnnm and P21nm) are 3
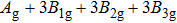 and 3
and 3
 , which deviate from calculated ones since different symmetries are involved. Nevertheless, the variance is quite acceptable as the major difference between experimental and calculated structures is the
, which deviate from calculated ones since different symmetries are involved. Nevertheless, the variance is quite acceptable as the major difference between experimental and calculated structures is the
 angle which distorts within a range of 3 degrees.
angle which distorts within a range of 3 degrees.
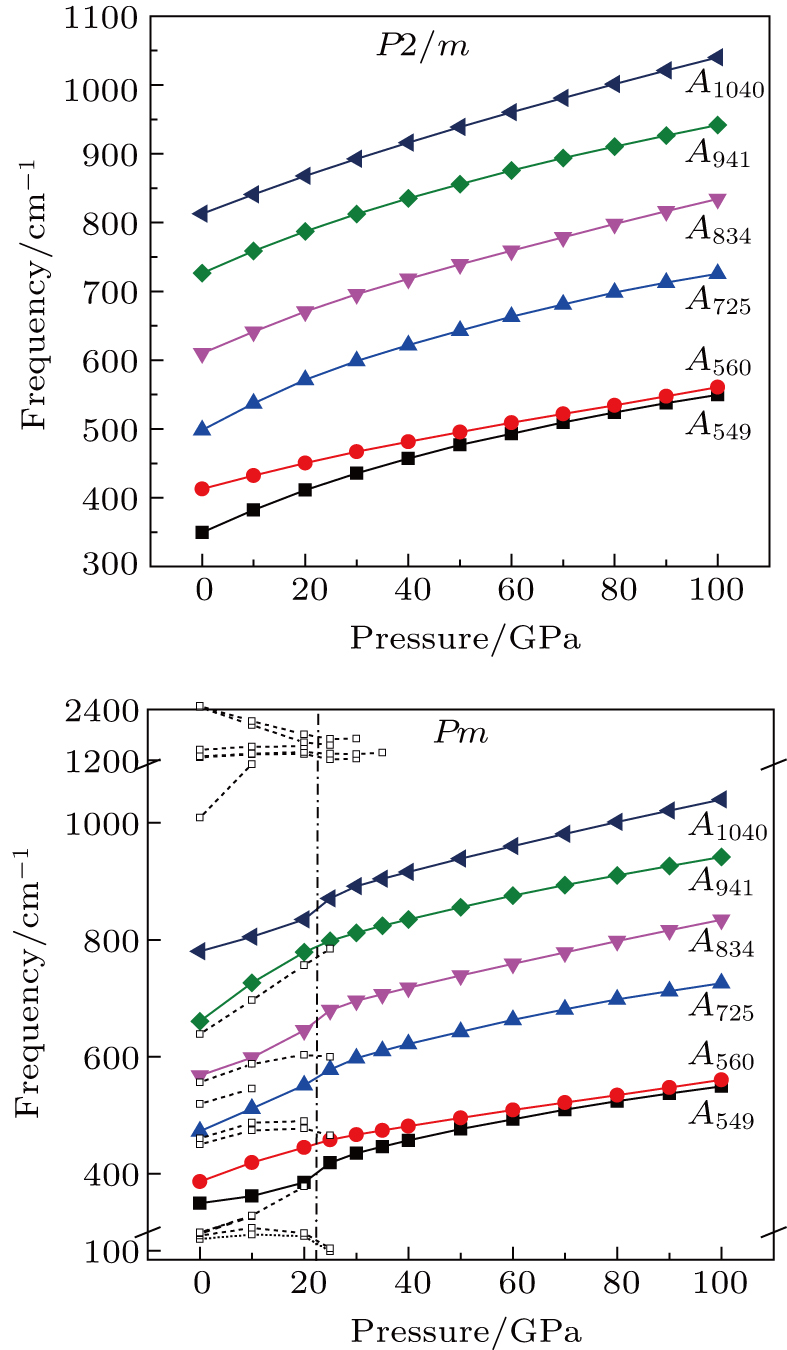
Raman frequencies of the two phase H structures are calculated and plotted each as a function of pressure in Fig. 8. The number of active Raman modes for
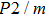 symmetry remains constant in a pressure range from 0 GPa to 100 GPa. In addition, the vibrational frequencies increase with the augment of pressure, which is normal behavior resulting from the increased repulsion between neighbor atoms.[46] The intensities of all Raman-active modes except for
symmetry remains constant in a pressure range from 0 GPa to 100 GPa. In addition, the vibrational frequencies increase with the augment of pressure, which is normal behavior resulting from the increased repulsion between neighbor atoms.[46] The intensities of all Raman-active modes except for
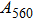 decrease under pressure (Supplement Tables A4, A5, and A6 in Appendix A). As for
decrease under pressure (Supplement Tables A4, A5, and A6 in Appendix A). As for
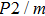 symmetry, all Raman modes (Fig. 7) are only related to the motion of oxygen atoms. No contributions from the motions of Mg, Si, and H atoms are detected. The
symmetry, all Raman modes (Fig. 7) are only related to the motion of oxygen atoms. No contributions from the motions of Mg, Si, and H atoms are detected. The
 and
and
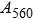 modes only have atomic vibrations parallel to the c axis, and the
modes only have atomic vibrations parallel to the c axis, and the
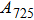 ,
,
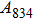 ,
,
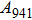 , and
, and
 modes only have atomic vibrations perpendicular to the c axis. Raman intensities for vibrations parallel to c axis (
modes only have atomic vibrations perpendicular to the c axis. Raman intensities for vibrations parallel to c axis (
 and
and
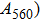 are smaller than those of vibrations perpendicular to c axis (
are smaller than those of vibrations perpendicular to c axis (
 ,
,
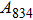 ,
,
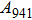 , and
, and
 modes) (Supplement Table A4 in Appendix A). The results suggest that the Raman vibration in phase H with symmetric hydrogen bonds is mainly controlled by displacements of oxygen atoms parallel to (001) plane.
modes) (Supplement Table A4 in Appendix A). The results suggest that the Raman vibration in phase H with symmetric hydrogen bonds is mainly controlled by displacements of oxygen atoms parallel to (001) plane.
At 0 GPa, 21 Raman modes are observed in phase H with Pm symmetry. These modes can be classified as two groups. Group 1 includes 15 vibrational modes with frequencies ranging from 226 cm
 to 780 cm
to 780 cm
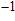 . The rest of these modes with frequencies in a range from 1009 cm
. The rest of these modes with frequencies in a range from 1009 cm
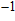 to 2470 cm
to 2470 cm
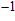 belong to group 2. Distortions and relative displacements of Si (or Mg) and O are observed in group 1 while only displacement of H, stretching and bending of hydrogen bonds are observed in group 2. The O–H stretching modes (
belong to group 2. Distortions and relative displacements of Si (or Mg) and O are observed in group 1 while only displacement of H, stretching and bending of hydrogen bonds are observed in group 2. The O–H stretching modes (
 and
and
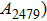 have the maximal intensities, because of the long-range electrostatic interactions between O–H groups.[41]
have the maximal intensities, because of the long-range electrostatic interactions between O–H groups.[41]
The vibrational patterns of Pm symmetry can be divided into two stages: from 0 GPa to 30 GPa and from 30 GPa to 100 GPa (Fig. 8), according to the symmetrization of hydrogen bonds at about 30 GPa. All the vibrational modes belonging to group 2 (in a frequency range from 1009 cm
 to 2479 cm
to 2479 cm
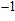 ) disappear at pressures higher than 30 GPa. The reason is that the reduction of
) disappear at pressures higher than 30 GPa. The reason is that the reduction of
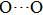 distances and the symmetrization of hydrogen bonds restrict the ability for hydrogen atoms to motion.[47] Besides, 8 vibrational modes in group 1 which relate to the motions of Mg or Si atoms vanish before being pressurized to 30 GPa. Finally, in the Pm symmetry there are only 6 vibration modes (
distances and the symmetrization of hydrogen bonds restrict the ability for hydrogen atoms to motion.[47] Besides, 8 vibrational modes in group 1 which relate to the motions of Mg or Si atoms vanish before being pressurized to 30 GPa. Finally, in the Pm symmetry there are only 6 vibration modes (
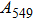 ,
,
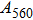 ,
,
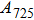 ,
,
 ,
,
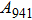 , and
, and
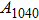 ) that remain Raman-active, the number of which modes (i.e., 6) is exactly the number of vibration modes that are Raman active in the
) that remain Raman-active, the number of which modes (i.e., 6) is exactly the number of vibration modes that are Raman active in the
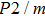 symmetry. Despite the obvious differences between Raman spectra at 0 GPa, the Raman frequencies and intensities for Pm and
symmetry. Despite the obvious differences between Raman spectra at 0 GPa, the Raman frequencies and intensities for Pm and
 symmetry are quite alike at pressures higher than 30 GPa (Supplement Tables A4, A5, and A6 in Appendix A).
symmetry are quite alike at pressures higher than 30 GPa (Supplement Tables A4, A5, and A6 in Appendix A).
Six Raman modes:
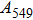 ,
,
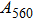 ,
,
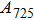 ,
,
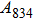 ,
,
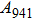 , and
, and
 of Pm symmetry are taken into account for calculating the pressure derivatives (
of Pm symmetry are taken into account for calculating the pressure derivatives (
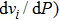 in a pressure range from 0 GPa to 100 GPa because the remaining modes vanish under high pressures (
in a pressure range from 0 GPa to 100 GPa because the remaining modes vanish under high pressures (
 GPa) (Table 1). The pressure derivatives of all modes for phase H are positive, which implies the strengthening of the structure.[48] Unlike the Raman shift frequency of
GPa) (Table 1). The pressure derivatives of all modes for phase H are positive, which implies the strengthening of the structure.[48] Unlike the Raman shift frequency of
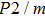 symmetry which is linearly dependent on pressure, the pressure derivatives of Pm symmetry can be classified as 2 groups. At low pressures (< 25 GPa), the pressure derivatives of Raman frequencies for Pm symmetry are larger than those for
symmetry which is linearly dependent on pressure, the pressure derivatives of Pm symmetry can be classified as 2 groups. At low pressures (< 25 GPa), the pressure derivatives of Raman frequencies for Pm symmetry are larger than those for
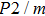 symmetry. Also, the derivatives for both structures become similar at high pressures (>30 GPa). A conspicuous jump of frequencies for Pm structure takes place at pressures between 25 GPa to 30 GPa, which corresponds to symmetrization of hydrogen bonds.
symmetry. Also, the derivatives for both structures become similar at high pressures (>30 GPa). A conspicuous jump of frequencies for Pm structure takes place at pressures between 25 GPa to 30 GPa, which corresponds to symmetrization of hydrogen bonds.
Table 3.
Table 3.
 | Table 3.
Pressure shifts of the Raman modes of phase H.
. |
4. Conclusions and perspectivesThe phase H (MgSiO
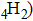 , as an important candidate for transporting water into the deep Earth, is stable at pressures greater than the stability field of phase D, and separately discussed to evaluate its structure stability, elastic properties and the possibility of forming a solid solution with
, as an important candidate for transporting water into the deep Earth, is stable at pressures greater than the stability field of phase D, and separately discussed to evaluate its structure stability, elastic properties and the possibility of forming a solid solution with
 -AlOOH in the lower mantle condition.[14–16] In order to understand the stability of phase H under high pressure, first-principles simulations are carried out to investigate the structural, elastic, and vibrational properties of phase H with the two possible symmetric structures: Pm and
-AlOOH in the lower mantle condition.[14–16] In order to understand the stability of phase H under high pressure, first-principles simulations are carried out to investigate the structural, elastic, and vibrational properties of phase H with the two possible symmetric structures: Pm and
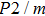 . The results indicate that the two structures show similar structural parameters, elastic and vibrational properties at pressures higher than 30 GPa. The reason is the symmetrization of hydrogen bonds. The symmetrization of hydrogen bonds also generally takes place in plenty of minerals under high pressure, such as ice,
. The results indicate that the two structures show similar structural parameters, elastic and vibrational properties at pressures higher than 30 GPa. The reason is the symmetrization of hydrogen bonds. The symmetrization of hydrogen bonds also generally takes place in plenty of minerals under high pressure, such as ice,
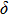 -AlOOH and hydrous silica.[36,38]
-AlOOH and hydrous silica.[36,38]
The
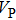 and
and
 of phase H with Pm symmetry sharply increase from 25 GPa to 30 GPa compared with those with
of phase H with Pm symmetry sharply increase from 25 GPa to 30 GPa compared with those with
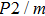 symmetry, and when pressure is larger than 30 GPa, the values of
symmetry, and when pressure is larger than 30 GPa, the values of
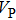 and
and
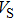 of Pm and
of Pm and
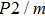 symmetry are almost identical. In other words, the symmetrization of hydrogen bonds made the seismic velocities of phase H increase. Therefore, the symmetrization of hydrogen bonds in dense hydrous silicate may lead to the abnormal pressure dependence of
symmetry are almost identical. In other words, the symmetrization of hydrogen bonds made the seismic velocities of phase H increase. Therefore, the symmetrization of hydrogen bonds in dense hydrous silicate may lead to the abnormal pressure dependence of
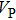 and
and
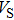 and the formation of a high-velocity layer in the mantle. The azimuthal anisotropies for phase H are
and the formation of a high-velocity layer in the mantle. The azimuthal anisotropies for phase H are
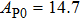 %,
%,
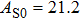 % (
% (
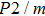 ) and
) and
 %,
%,
 % (Pm) at 0 GPa, and increase to
% (Pm) at 0 GPa, and increase to
 %,
%,
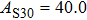 % (
% (
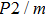 symmetry) and
symmetry) and
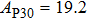 %,
%,
 % (Pm symmetry) at 30 GPa. So phase H might be one of the sources of the velocity anomalies and anisotropy in the upper part of the lower mantle. Compared with phase D and
% (Pm symmetry) at 30 GPa. So phase H might be one of the sources of the velocity anomalies and anisotropy in the upper part of the lower mantle. Compared with phase D and
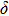 -AlOOH, phase H shows small density but fast seismic velocity, which might contribute to the anomalous phenomenon of seismic velocity in the lower mantle.
-AlOOH, phase H shows small density but fast seismic velocity, which might contribute to the anomalous phenomenon of seismic velocity in the lower mantle.
Raman spectra of phase H show the effects of symmetrization of hydrogen bonds on vibrational frequency and intensity. At 0 GPa, 21 Raman modes are observed in phase H with Pm symmetry. As for
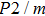 symmetry, 6 Raman modes are observed at 0 GPa. However, only 6 Raman modes in each phase H with Pm-to-
symmetry, 6 Raman modes are observed at 0 GPa. However, only 6 Raman modes in each phase H with Pm-to-
 symmetry are detected under higher pressure (
symmetry are detected under higher pressure (
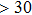 GPa). When pressure is higher than 30 GPa, Raman frequencies of Pm symmetry are the same as those of
GPa). When pressure is higher than 30 GPa, Raman frequencies of Pm symmetry are the same as those of
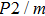 symmetry, which indicates the transformation from Pm to
symmetry, which indicates the transformation from Pm to
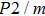 symmetry as a result of symmetrization of hydrogen bonds. The values of pressure derivative
symmetry as a result of symmetrization of hydrogen bonds. The values of pressure derivative
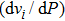 of all Raman modes are positive. All these results conduce to the understanding of the stability of phase H in the mantle.
of all Raman modes are positive. All these results conduce to the understanding of the stability of phase H in the mantle.