† Corresponding author. E-mail:
Based on the density functional theory, the influences of strain on structural, elastic, thermal and optical properties of CuGaTe2 are discussed in detail. It is found that the tensile strain on CuGaTe2 is beneficial to the decrease of lattice thermal conductivity by reducing the mean sound velocity and Debye temperature. Moreover, all strained and unstrained CuGaTe2 exhibit rather similar optical characters. But the tensile strain improves the ability to absorb sunlight in the visible range. These research findings can give hints for designing thermoelectric and photovoltaic devices.
The energy crisis and environmental pollution are increasingly serious. How to properly solve the energy shortage and environmental pollution is a worldwide concern. Photovoltaic and thermoelectric materials are both new energy materials, which can convert solar energy and industrial waste heat into available electric energy, respectively. It is most important and difficult to improve the conversion efficiencies of these new energy materials now.
Recently, the ternary chalcopyrite I–III–V I2 (I = Cu, Ag; III = Al, Ga, In; and V I = S, Se, Te) has been of wide interest, since it is a kind of potential photovoltaic and thermoelectric (TE) material,[1–3] due to the unique structural properties. As a thermoelectric material, it shows excellent thermoelectric performance in the intermediate temperature range. For example, the maximum dimensionless figure of merit for CuGaTe2 reached 1.4 experimentally[2] and 1.69 theoretically[3] at 950 K. In theory, Shen et al. proved that doping Zn and Mn at Ga sites can effectively tune carrier concentration and reduce the lattice thermal conductivity based on a single parabolic band approximation.[4] Rai et al. investigated the thermoelectric properties of bulk and surface (001) CuInTe2 by the first principles calculation and suggested the key to improving their thermoelectric performance was to increase the Seebeck coefficient and electrical conductivity.[5] The ternary chalcopyrite is also extensively used in photovoltaic applications, especially CuInSe2, due to its high conversion efficiency.[6] Zhang et al. employed the density functional theory (DFT) and discussed the structural and optical properties of CuXTe2 (X = Al, Ga, In).[7] With recent development, the current best efficiency for sulfide thin film solar cell was 12.3%.[8] However, this efficiency is still much lower than the reported efficiency of other thin-film solar cells, such as 18.3% for CdTe.
It is reported that the semiconductor material, as a candidate used in photovoltaic or thermoelectric technology, is recognized by its energy band gap, optical and thermodynamic properties.[9,10] To our knowledge, many effective ways to adjust the electronic properties of semiconductors, such as doping,[11–13] pressure, and strain engineering have been proposed. Hinsche et al. focused on investigating the influence of strain on thermoelectric properties of Bi2Te3, Sb2Te3, and Si.[14,15] Our group studied the effect of strain on thermoelectric properties of CuGaTe2.[16] In this paper, we estimate the Seebeck coefficient of CuGaTe2, but do not discuss the effect on thermal conductivity. As far as we know, there are still no detailed theoretical studies on the influence of strain on optical and thermal properties up to now. Thus, we will focus on studying the effects of strain on elastic, thermal and optical properties of CuGaTe2 by the first principles calculation in this work.
The rest of the paper is organized as follows. In Section
The ball-and-stick structure model of CuGaTe2 is shown in Fig. 
In this paper, we will focus on discussing the influence of strain on elastic, thermal and optical properties of CuGaTe2. For this purpose, the employed computational approach is the first-principle calculations based on the density functional theory (DFT).[19] The calculations are performed with the CASTEP code. The details of parameter settings during the computational process are shown below. The exchange correlation functional is selected as the generalized gradient approximation of Perdew–Burke–Ernzerhof (GGA-PBE);[20] pseudo-potential is chosen as the ultrasoft pseudo-potential; the cut-off energy and a k mesh are set to be 500 eV and 5×5×3, respectively. The self-consistent convergence tolerance of the total energy, maximum force, maximum displacement and maximum stress are set to be 5×10−6 eV/atom, 0.01 eV/Å, 5×10−4 Å, and 0.02 GPa, respectively.[21] The electronic configurations are regarded as Cu 3d104s1, Ga 3d104s24p1, and Te 5s25p4 during the calculations.
In experiment, the strain may be caused by depositing CuGaTe2 thin film on the tops of different substrates. In order to simulate this situation, the strain ratio Δa/a is taken in a range from −2% (compressive strain) to 2% (tensile strain). The calculated values of lattice constant c and unit-cell volume V of strained and unstrained CuGaTe2 are shown in Fig.
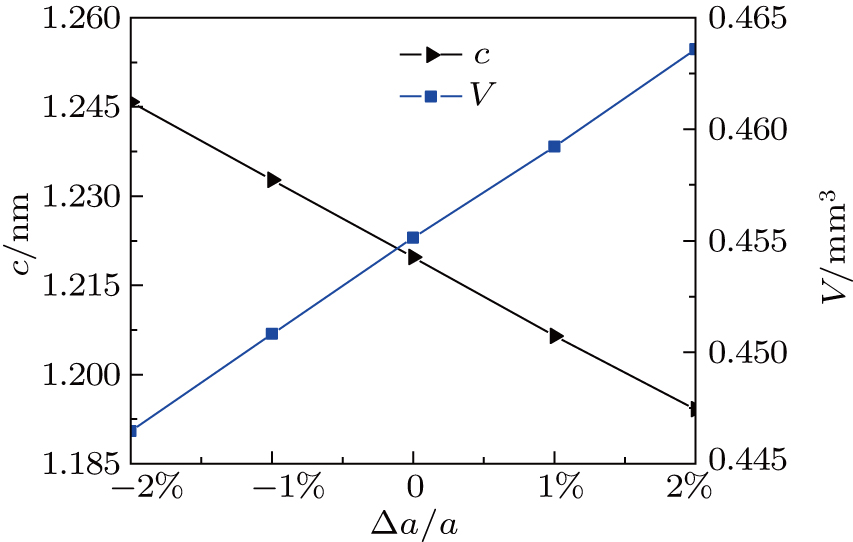 | Fig. 2. (color online) Optimized lattice constant c and unit-cell volume V of CuGaTe2 versus strain ratio Δa/a. |
Generally, elastic properties of a solid are very important because they conduce to understanding the mechanical stability and mechanical properties.[22] For a tetragonal crystal, six elastic constants are independent,[23] that is, C11, C12, C13, C33, C44, and C66.[22] The mechanical stability for a tetragonal crystal makes the following restrictions on the elastic constants:[24]
 |
The elastic constants of CuGaTe2 with no strain have been reported in Ref. [25]. The calculated results for the strained cases are listed in Table
| Table 1.
Values of elastic constants Cij and elastic moduli B, G (in unit GPa) for strained CuGaTe2. . |
From the Navier’s equation,[28] the transverse sound velocity vt and longitudinal sound velocity vl can be derived. The mean sound velocity vs can be obtained from
 |
The calculated values of mean sound velocities vs are listed in Table
| Table 2.
Values of the mean sound velocity vs, Debye temperature TD, and minimum thermal conductivity kmin for strained CuGaTe2. . |
The heat capacity is an important parameter for a substance, since it not only provides an essential insight into the vibrational properties but is also involved with many applications.[29] Applying the Debye approximation, the expression of constant-volume heat capacity Cv is given by
 |
where ξ = ħω/kBT, kB and R are the Boltzmann’s constant and gas constant, respectively. Besides, TD is the Debye temperature, which can be expressed as
 |
where h and NA are Plank’s and Avogadro’s constant, respectively; M is the relative molecular weight; n is the number of atoms in the molecule. The calculated values of Debye temperature TD are listed in Table
From the point of view of kinetic theory, the thermal conductivity is expressed as[30]
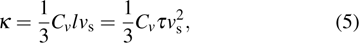 |
where Cv is the constant-volume heat capacity, l is the phonon mean free path, and τ is the average phonon lifetime. It is clearly indicated that the item 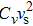

 | Fig. 3. (color online) Plots of temperature-dependent item 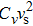
|
In addition, to quantitatively measure the effect of strain on thermal conductivity, the minimum thermal conductivity kmin is estimated using Cahill model.[31] Its specific expression can be written as
 |
where kB is the Boltzmann constant, vl and vs are longitudinal sound velocity and transverse sound velocity, and vt1 = vt2 = vt. The calculated values of minimum thermal conductivities for strained CuGaTe2 are listed in Table 
A photovoltaic material should satisfy some requirements: it should be a direct-gap semiconductor, have a band gap preferably large enough (close to 1.4 eV), large absorption coefficient to absorb the essential part of the visible light spectrum and small reflectance.[7] We have studied the energy bands of CuGaTe2 at various in-plane lattice parameters (−2%, −1%, 0, 1%, 2%) in Ref. [16] previously. Our results indicated that their energy bands are direct band gaps. The calculated value of band gap for unstrained CuGaTe2 is 0.095 eV. However, the experimental value is 1.23 eV.[32] So we set a scissor operator of 1.135 eV to overcome such a discrepancy. To model the broadening effect, the instrumental smearing of 0.25 eV is used in all cases.
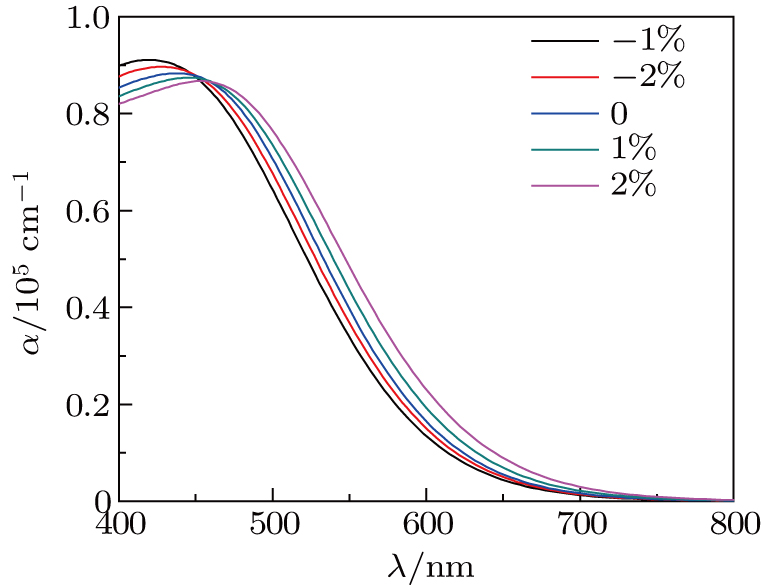
The absorption coefficient is a main optical characteristic of photovoltaic material to measure how far light can penetrate the material. The absorption coefficient α can be computed using the following equation:
 |
where ω is the frequency, ε1(ω) and ε2(ω) are the real part and imaginary part of the dielectric function, respectively. The absorption coefficient-dependence of the wavelength λ is shown in Fig.
We mainly discuss the influence of strain on structural, elastic, thermal and optical properties of CuGaTe2 based on the density functional theory in this work. The optimized out-of-plane lattice constant c decreases linearly with the increase of in-plane lattice constant a. But the unit-cell volume V is expanded. The calculated elastic constants for the strained and unstrained cases satisfy the mechanical stability. The values of sound velocities and Debye temperature are estimated by the obtained elastic constants. It is found that they both decrease with the increase of tensile strain. This means that applying tensile strain to CuGaTe2 is beneficial to reducing the thermal conductivity. Moreover, the tensile strain is helpful for improving the absorption of sunlight. These results give hints for designing the CuGaTe2 into good thermoelectric and photovoltaic materials.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] |