† Corresponding author. E-mail:
In this work, the effect of uniaxial strain on electronic and thermoelectric properties of magnesium silicide using density functional theory (DFT) and Boltzmann transport equations has been studied. We have found that the value of band gap increases with tensile strain and decreases with compressive strain. The variations of electrical conductivity, Seebeck coefficient, electronic thermal conductivity, and power factor with temperatures have been calculated. The Seebeck coefficient and power factor are observed to be modified strongly with strain. The value of power factor is found to be higher in comparison with the unstrained structure at 2% tensile strain. We have also calculated phonon dispersion, phonon density of states, specific heat at constant volume, and lattice thermal conductivity of material under uniaxial strain. The phonon properties and lattice thermal conductivity of Mg2Si under uniaxial strain have been explored first time in this report.
The materials which can directly convert heat into electricity and vice versa are called as thermoelectric materials. These materials have great interest in science community because of environmental issues and energy crisis. One important parameter, a dimensionless figure of merit[1] gauges the performance of thermoelectric materials, which is defined as
 |
where S is Seebeck coefficient (in unit V/K), σ is electrical conductivity (in unit S/m), k is total thermal conductivity (in unit W/mK), and T is temperature (in unit K) respectively. Good thermoelectric materials have high thermo power and low thermal conductivity.
Owing to their non toxic nature, thermal stability, low density, relative abundance, and low cost of production, magnesium silicide and related alloys have become promising material for thermoelectric applications. Mg2Si material has been considered as a high performance thermoelectric material in the temperature range of 500 K–800 K.[2,3] We have already discussed the importance and applications of Mg2Si in our previous work.[4] In our earlier studies,[4] we have reported that the value of figure of merit is 1.83 × 10−3 at 1000 K for pure Mg2Si. This value is very low as compared to other thermoelectric materials. So to enhance the figure of merit, there are various methods proposed. To improve the thermoelectric efficiency, the electronic band engineering via electronic doping, introduction of resonant levels in the electronic density of state is widely explored.[5–7] Mechanical stress applied to the materials induces a modification in the electronic band structure which may improve the thermoelectric properties.[8,9] Under the effect of mechanical stress (pressure and strain), the bands of material are shifted, splitted, and the effective mass changes. These changes affect the thermoelectric properties. Balout et al.[10,11] have studied the electronic and thermoelectric properties of Mg2Si under isotropic strain. They found that under the effect of isotropic strain the Seebeck coefficient and power factor values increase by 40% and 100% respectively as compared to the unstrained Mg2Si. Balout and his coworkers[12] found the thermoelectric properties of Mg2Si under uniaxial [100] strains versus (100) oriented thin films. The electronic and electronic transport properties of this material under uniaxial strain with different concentration have been already discussed in previous literature.[12] But the variation of electronic thermoelectric properties with temperature and lattice thermal conductivity, specific heat, phonon dispersion curves, and phonon density of states of Mg2Si material with temperature and strain have not been studied yet as per our knowledge. The purpose of present study is to give a comprehensive description of the electronic and thermoelectric properties of Mg2Si under uniaxial strain. In this work the following points have been systematically explored: The effect of uniaxial strain on the electronic and thermoelectric properties of Mg2Si. Evaluation of the lattice thermal conductivity, specific heat, phonon dispersion relation, and phonon density of states of strained Mg2Si material.
This paper is organized as: In the following section, computational approach is discussed. Thereafter, calculations for electronic and thermoelectric properties are given in Section
In our calculations, the electronic structure calculations were carried out using density functional theory (DFT) based on plane wave pseudo-potential method as implemented in the Quantum Espresso package.[13] The generalized gradient approximation (GGA)[14] of Perdew–Burke–Ernzerhof (PBE) was used for exchange–correlation functional. The cutoff for the kinetic energy was set to 40 Ry (1 Ry = 13.6056923 eV) for the plane-wave expansion of the electronic wave functions. The charge–density cutoff was kept at 400 Ry and the Marzari-vanderbilt cold smearing size was fixed at 0.003 Ry. The Brillouin zone integration was performed using Monkhorst–Pack scheme[15] with 4 × 8 × 8 meshes. For the density of state (DOS) calculation, we used tetrahedron method with 16 × 16 × 16 denser k-point mesh.
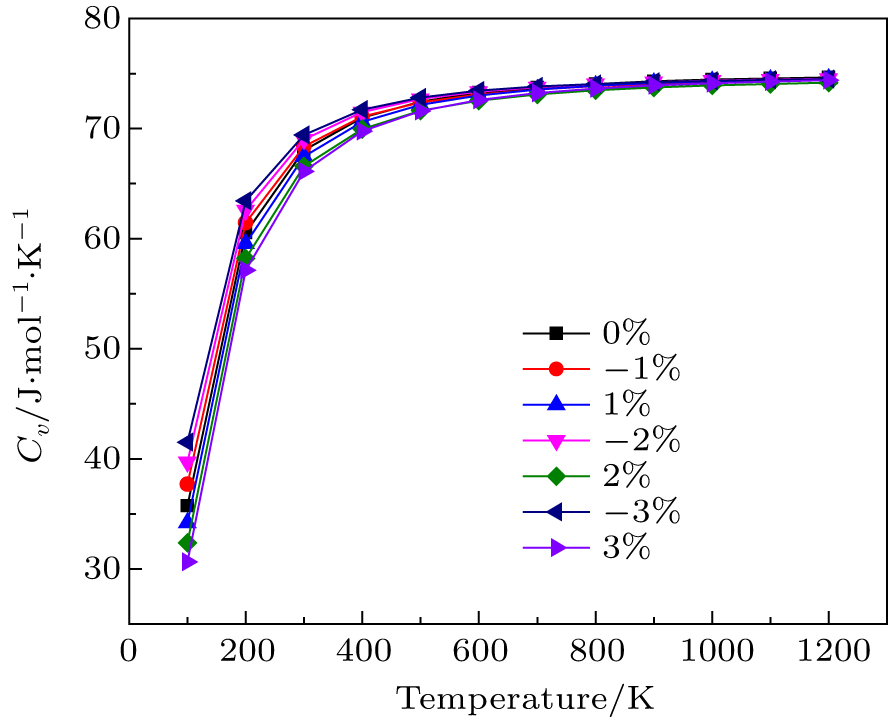
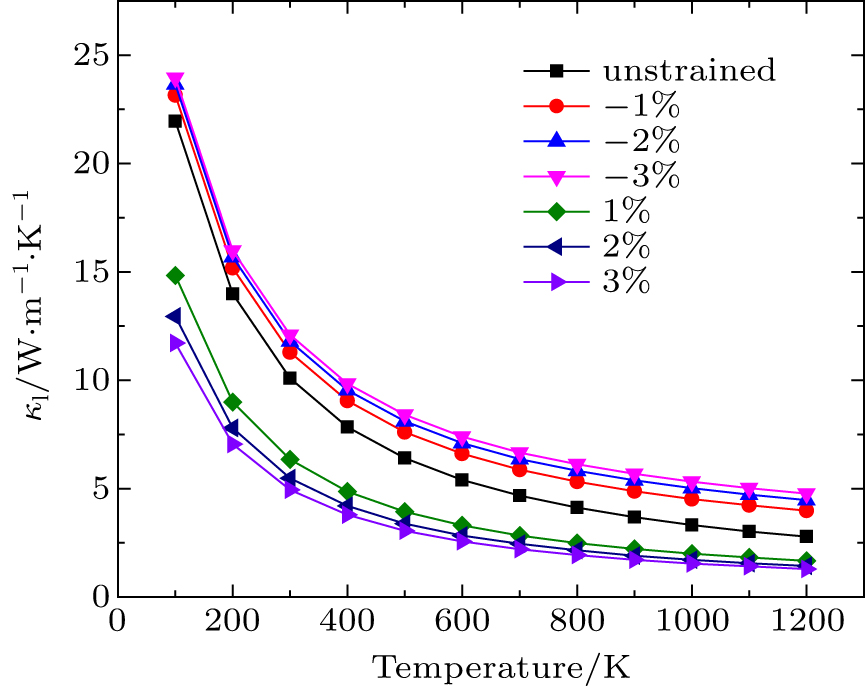
BoltzTraP code[16] was used to calculate the thermoelectric properties. The detail description of methodology is given in our previous work.[4,17,18] To calculate lattice thermal conductivity (kl), ShengBTE code[19] based on phonon Boltzmann transport equation (pBTE) has been used. The phonon properties have been calculated using density functional perturbation theory (DFPT).[20] The dynamical matrices have been calculated for 4 × 4 × 4 q-points grid generated according to Monkhorst and pack.[15] Quasi harmonic approximation (QHA)[21] implemented in Quantum espresso Code[13] has been used to calculate the specific heat of the lattice.
Pristine Mg2Si is a face centered cubic structure with space group Fm3m. The calculated lattice constant of Mg2Si is 6.364 Å.[4] We have applied uniaxial strain on Mg2Si. In uniaxial strain, tensile and compressive strains correspond to Δa0/a0 > 0 and Δa0/a0 < 0, where a0 is the lattice parameter of unstrained structure. Figure
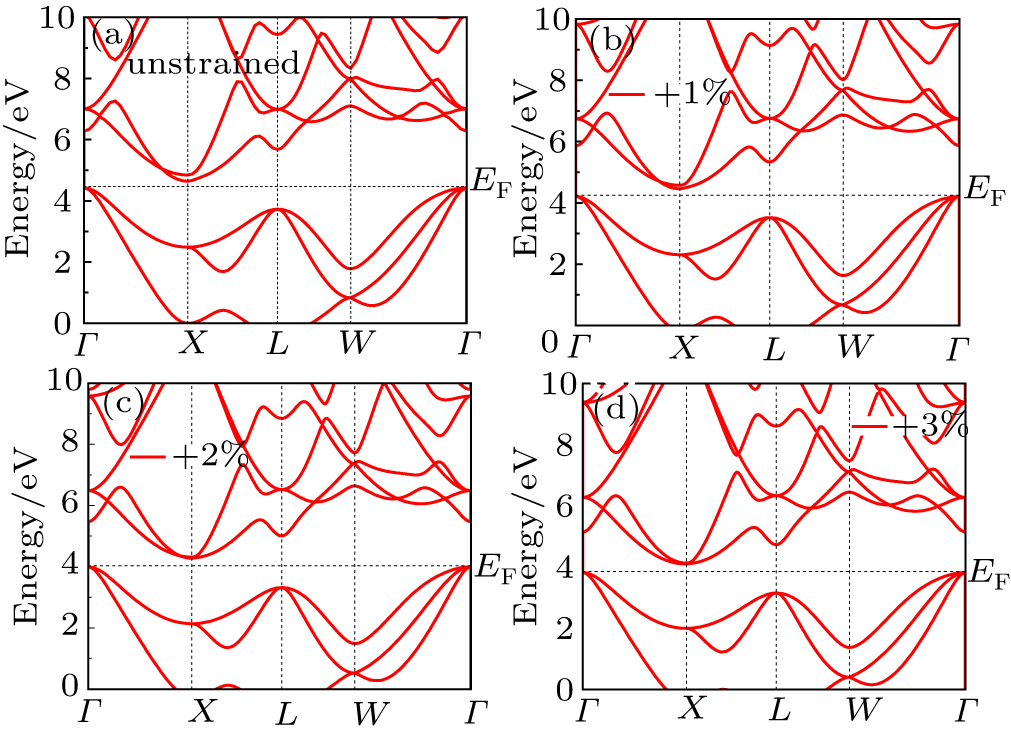 | Fig. 2. (color online) Electronic band structure of uniaxial tensile strain: (a) unstrained, (b) 1%, (c) 2%, (d) 3%. |
 | Fig. 3. (color online) Electronic band structure of Mg2Si under uniaxial compressive strain: (a) unstrained, (b) −1%, (c) −2%, (d) −3%. |
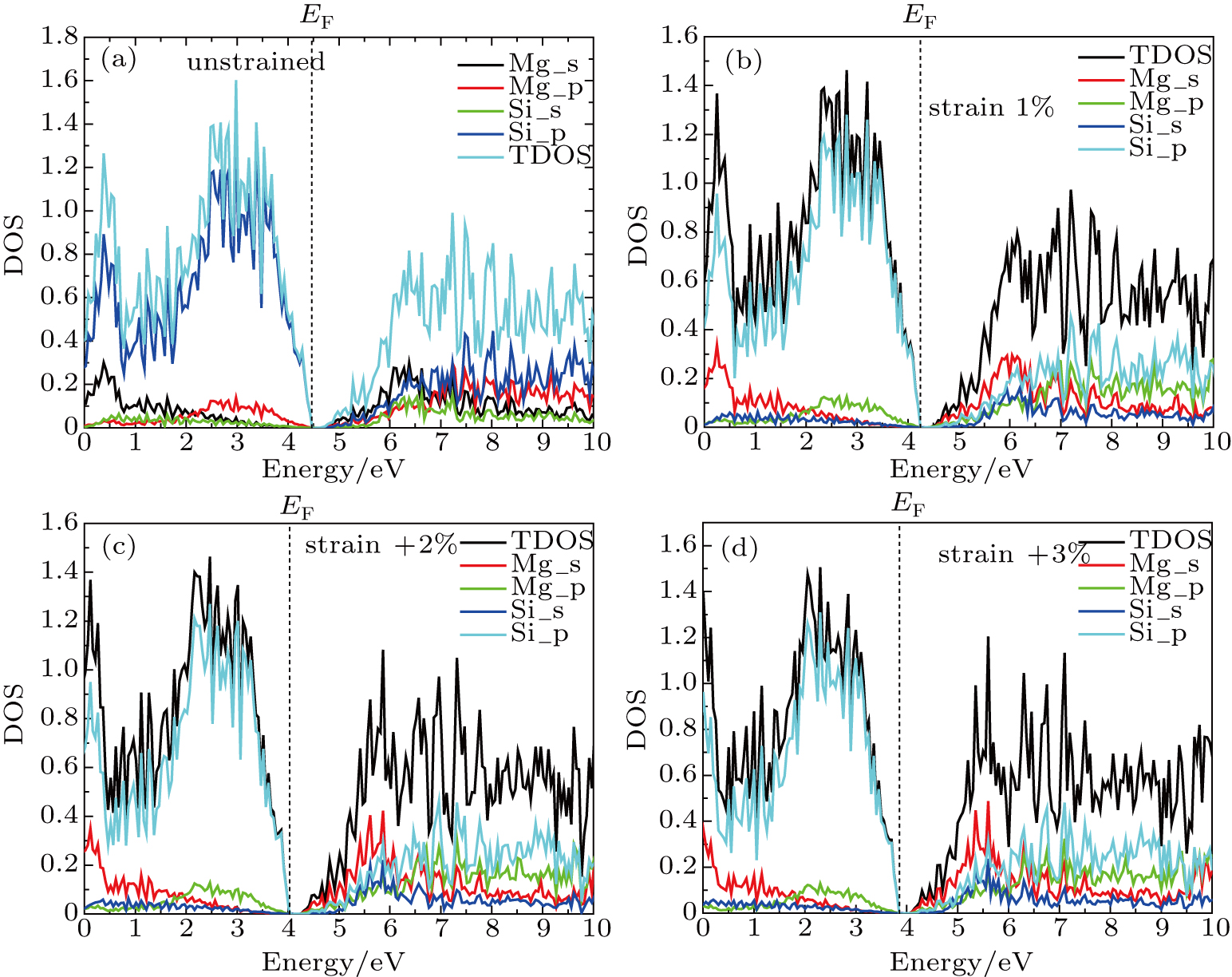 | Fig. 4. (color online) Density of states and PDOS of Mg2Si under uniaxial tensile strain: (a) unstrained, (b) −1%, (c) −2%, (d) −3%. |
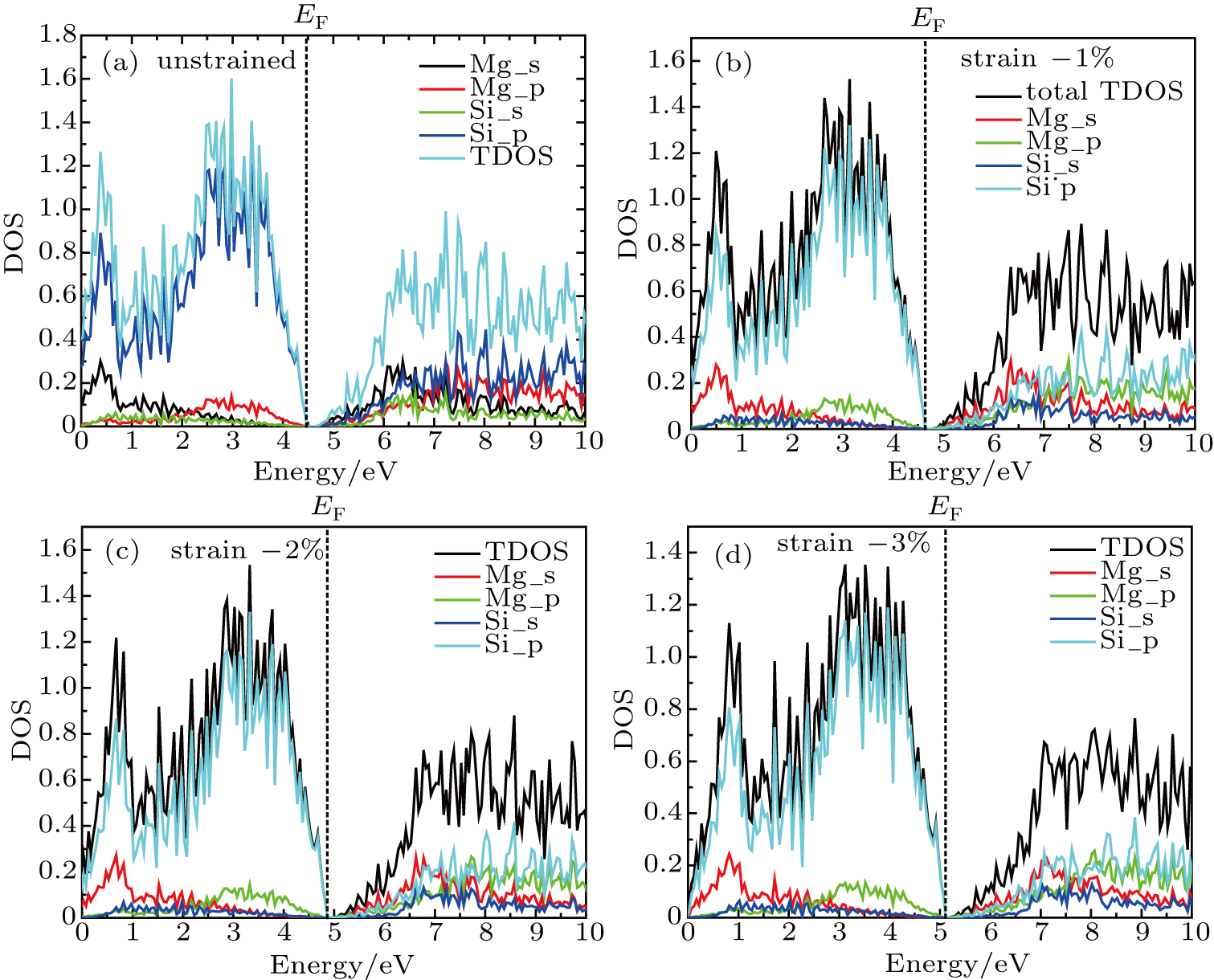 | Fig. 5. (color online) Density of states and PDOS of Mg2Si under uniaxial compressive strain: (a) unstrained, (b) −1%, (c) −2%, (d) −3%. |
In case of tensile strain (Fig.
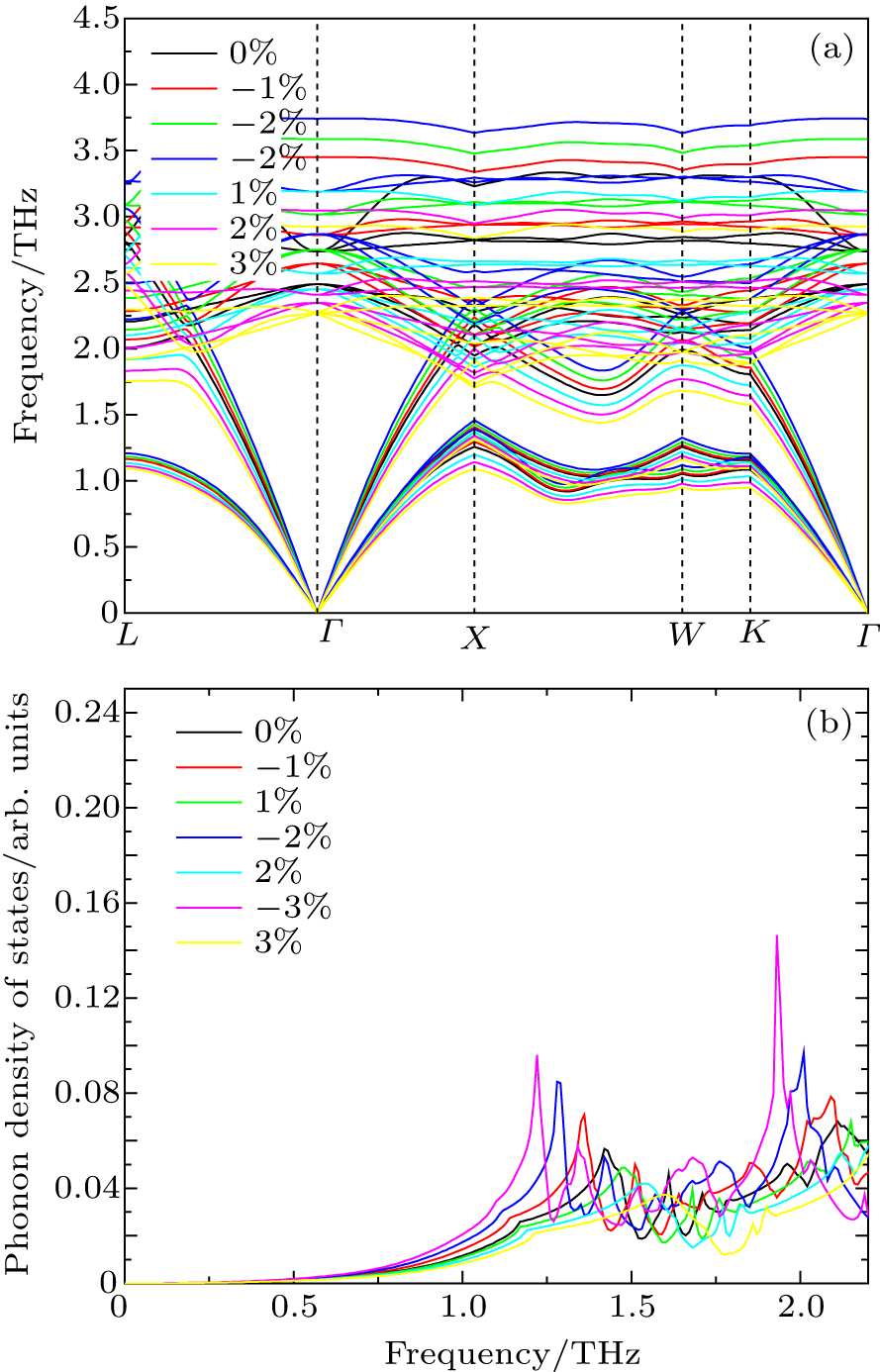
Under the effect of uniaxial strain, the shape of conduction band plays main role to enhance the thermoelectric performance of Mg2Si. In this study, we have noticed that the size of conduction band is affected by the compressive and tensile strains at high symmetry point X. Figure
In Fig.
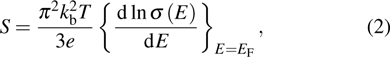 |
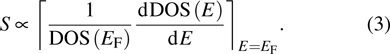 |
These equations show that S, directly depends upon the derivative of DOS and is inversely proportional to the DOS at Fermi level.[24,25] In general, as the density of carriers and the doping level increases, the electrical conductivity increases but the value of Seebeck coefficient decreases. Equation (
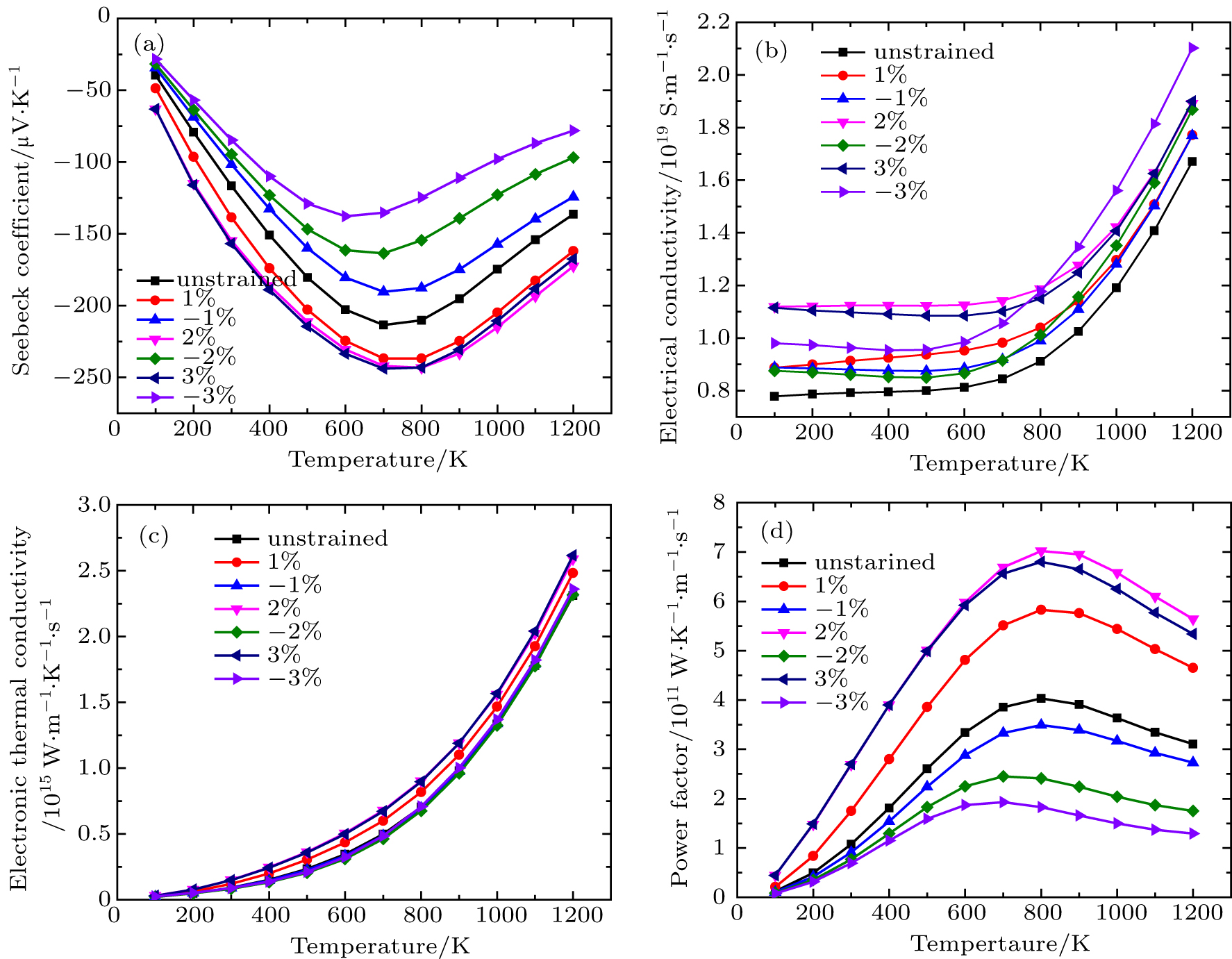
Under tensile strain, the Seebeck coefficient increases. It is apparent that a tensile strain tends to enhance the absolute value of the Seebeck coefficient. There is significant enhancement in the Seebeck coefficient as compared to strain free material. This is due to the fact that the Seebeck coefficient is proportional to the energy logarithmic derivative of the density of states at the Fermi level (as explained above). The variation of the Seebeck coefficient is related to the modification of density of states near the Fermi level.
When electronic bands become steeper, the density of states decreases and the Seebeck coefficient also decreases. In the compressive strain, the electronic bands become steeper which cause to decrease in the Seebeck coefficient. At high temperature, at 2% strain the value of the Seebeck coefficient is large as compared to other values.
The variation of the electrical conductivity with temperature and strains is depicted in Fig.
Figure
Figure
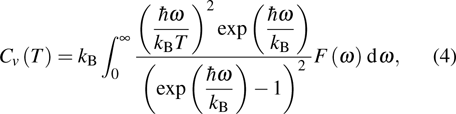 |
Figure
In this work, an attempt is made to employ first-principle calculations in order to predict the effect of uniaxial strain on Mg2Si. Up to 3% strain, the material remains semiconductor. The band gap increases or decreases under tensile strain or compressive strain. The most remarkable result is that a substantial improvement is observed for the Seebeck coefficient when the tensile strain is applied to material. The power factor is almost doubled compared to unstrained material. Under compressive and tensile strain, the electrical conductivity increases. This result could be attractive for the tensile strain that leads to the improvement in the power factor of material. The specific heat of Mg2Si increases with the increase in the compressive strain and decreases with the increase in the tensile strain. The lattice thermal conductivity decreases continuously when the applied strain is changed from compressive strain to tensile strain due to the shift of phonon dispersion curves under the strain. Tuning of electronic and thermal conductivities of bulk materials under strains has lot of applications in energy conversion and thermal management. This work may serve as an increase for researchers in future.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] |