† Corresponding author. E-mail:
The first-principles methods have been employed to calculate the structural, electronic, and mechanical properties of the α, β, and γ phases of uranium under pressure up to 100 GPa. The electronic structure has been viewed in forms of density of states and band structure. The mechanical stability of metal U in the α, β, and γ phases have been examined. The independent elastic constants, polycrystalline elastic moduli, as well as Poisson’s ratio have been obtained. Upon compression, the elastic constants, elastic moduli, elastic wave velocities, and Debye temperature of α phase are enhanced pronouncedly. The value of B/G illustrates that α and γ phases are brittle in ground state.
Actinide elements and their compounds exhibit many fascinating physical behaviors and play special role in nuclear applications,[1–8] for example, the superconductivity of the f-electron system,[9] the complex magnetic structure in neptunium dioxide,[10] and the topological electronic states in actinide nitrides.[11] Among them, element uranium has attracted many attentions.[12–18]
At ambient condition, the itinerant nature of U-5 f electrons results in a complex arrangement of atomic structure,[12–15] a low symmetrical crystal structure of face-centered orthohombic (fco). This phase, α-U, is stable in wide temperature range of 0 K–935 K and wide pressure area up to at least 100 GPa. At ambient pressure and under a narrow temperature range of 935 K–1045 K, a much complex β phase appears.[13,19] Under further high temperature of 1045 K–1460 K, in analogy to the transition metals of Ti, Zr, and Hf,[20,21] β-U transits to a simple high-symmetry structure of body-centered cubic (bcc). The driving mechanism for this kind of transition has been attributed to the electron localization[22] and/or the phonon-phonon interaction.[23]
Concerning the physical properties, in experiments, the charge density wave (CDW) state below 43 K,[24] bulk modulus and equation of state,[12–15] phase diagram at high pressure and temperature,[13] phonon-dispersion carves,[25,26] and heat capacity[27] of uranium were measured by ultrasonic technique, diamond anvil cell, x-ray diffraction, inelastic neutron scattering. In theory, the adiabatic compression curve up to 100 GPa,[16] effects of spin-orbit coupling,[17] mechanical properties,[18,28,29] melting,[30] optical properties,[31] work function,[32] and phonon spectra,[18,23,33] CDW,[34–36] and electron–phonon coupling[35] have been calculated in density-functional theory (DFT) level.
In this work, we use the first-principles DFT to carry out studies on the structural, electronic, and mechanical properties of uranium in its α, β, and γ phases under pressure up to 100 GPa. Specific details can be divided into four parts: (i) optimizing all lattice parameters and the internal degrees of freedom at selected volumes and then at our obtained pressures; (ii) comparing the enthalpy of the three phases to see the thermodynamic stability under pressure; (iii) analyzing the electronic structure; and (iv) calculating elastic constants and elastic moduli under different pressures.
We performed our first-principles DFT calculations within the Vienna ab initio simulation package (VASP).[37] The Perdew–Burke–Ernzerhof[38] form of the generalized gradient approximation was selected to described the exchange and correlation effects. A cutoff energy of 500 eV was set for the plane wave integration. All atoms were fully relaxed when Hellmann–Feynman forces become less than 0.01 eV/Å. The k-point meshes in the full wedge of the Brillouin zone (BZ) were sampled by 11×7×7, 7×7×13, and 13×13×13 grids, respectively for α, β, and γ phases according to the Monkhorst–Pack (MP)[39] scheme. The U 6s27s26p66d25f2 orbitals were treated as valence electrons.
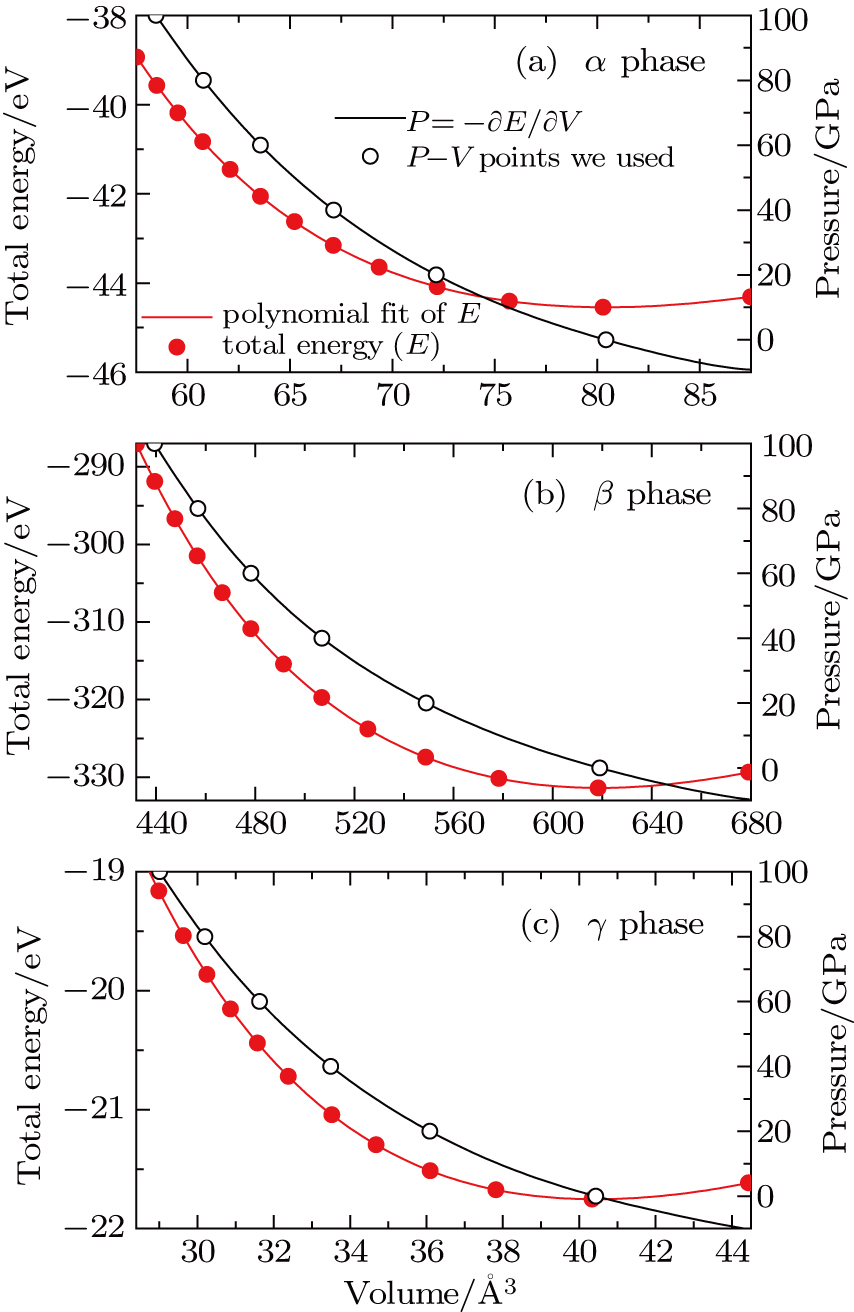
To avoid the Pulay stress trouble, the geometry optimization was performed on the basis of fixed volumes rather than constant pressures. As shown in Fig.
In order to calculate elastic constants, we can apply stress tensors with a small strain onto the equilibrium structure. According to Hooke’s law, the crystal energy is expanded by Taylor,[40]
 |
where E(V0,0) is the energy of the unstrained system with the equilibrium volume V0, ε is strain tensor which has matrix elements εij (i, j = 1, 2, and 3) defined by
 |
and Cij are the elastic constants. For orthorhombic α phase, there are nine independent elastic constants (C11, C22, C33, C44, C55, C66 C12, C13, and C23). They can be achieved from nine different strains listed in the following:
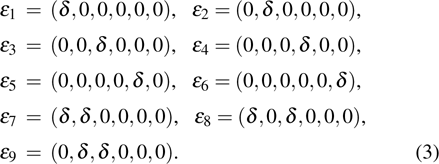 |
As for tetragonal β phase, there are six independent elastic constants (C11, C33, C44, C66 C12, and C13) and can be obtained from six different strains listed in the following:
 |
For cubic γ phase, there are three independent elastic constants (C11, C44, and C12) and can be gained from three different strains listed in the following:
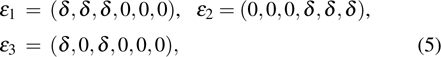 |
where the small strain δ was varied in steps of 0.006 from δ = −0.036 to δ = 0.036.
After having obtained the elastic constants, the polycrystalline bulk modulus B and shear modulus G were calculated from the Voigt–Reuss–Hill (VRH) approximations,[41–43] 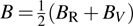

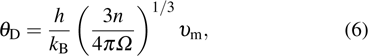 |
where h and kB are Planck and Boltzmann constants, respectively, n is the number of atoms in the molecule, Ω is molecular volume, and υm is the average sound wave velocity. The average wave velocity in the polycrystalline materials is approximately given by
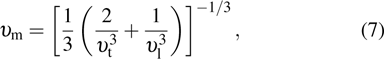 |
in the above expression, 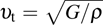
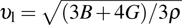
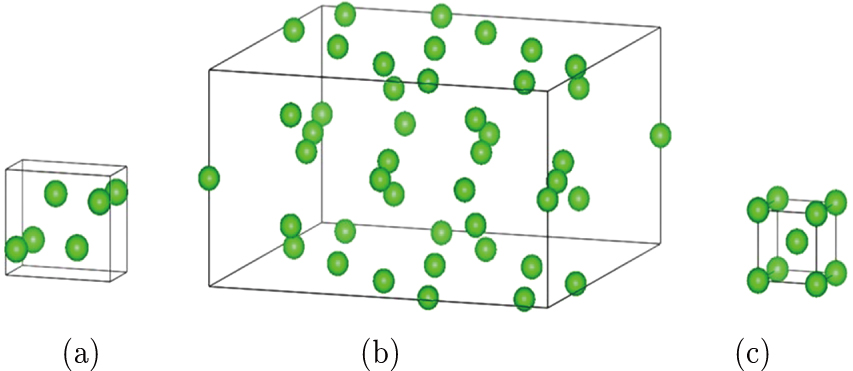
α-U crystallizes in the orthorhombic Cmcm space group (No. 63) with 4 atoms in the unit cell located at 4c (0, y, 0.25) Wyckoff positions [see Fig.
In Table
| Table 1.
Optimized lattice constants (a, b, and c), the fractional coordinate of the atoms (y), atomic volume (V) under pressures from 0 GPa to 100 GPa as well as bulk modulus (B) and its pressure derivative (B′) at 0 GPa for α, β, and γ phases of uranium. For comparison, experimental values and theoretical results from other calculations at 0 GPa are also listed. . |
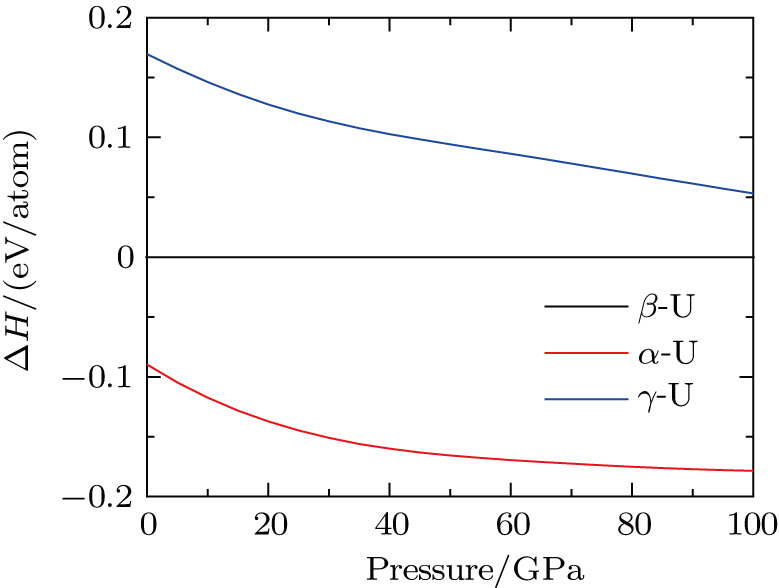
The thermodynamic stabilities of α, β, and γ phases under pressure up to 100 GPa can be judged by comparing the Gibbs free energy values. At 0 K, the the Gibbs free energy is equal to the enthalpy and can be obtained by G = H = E + PV. We plot in Fig.
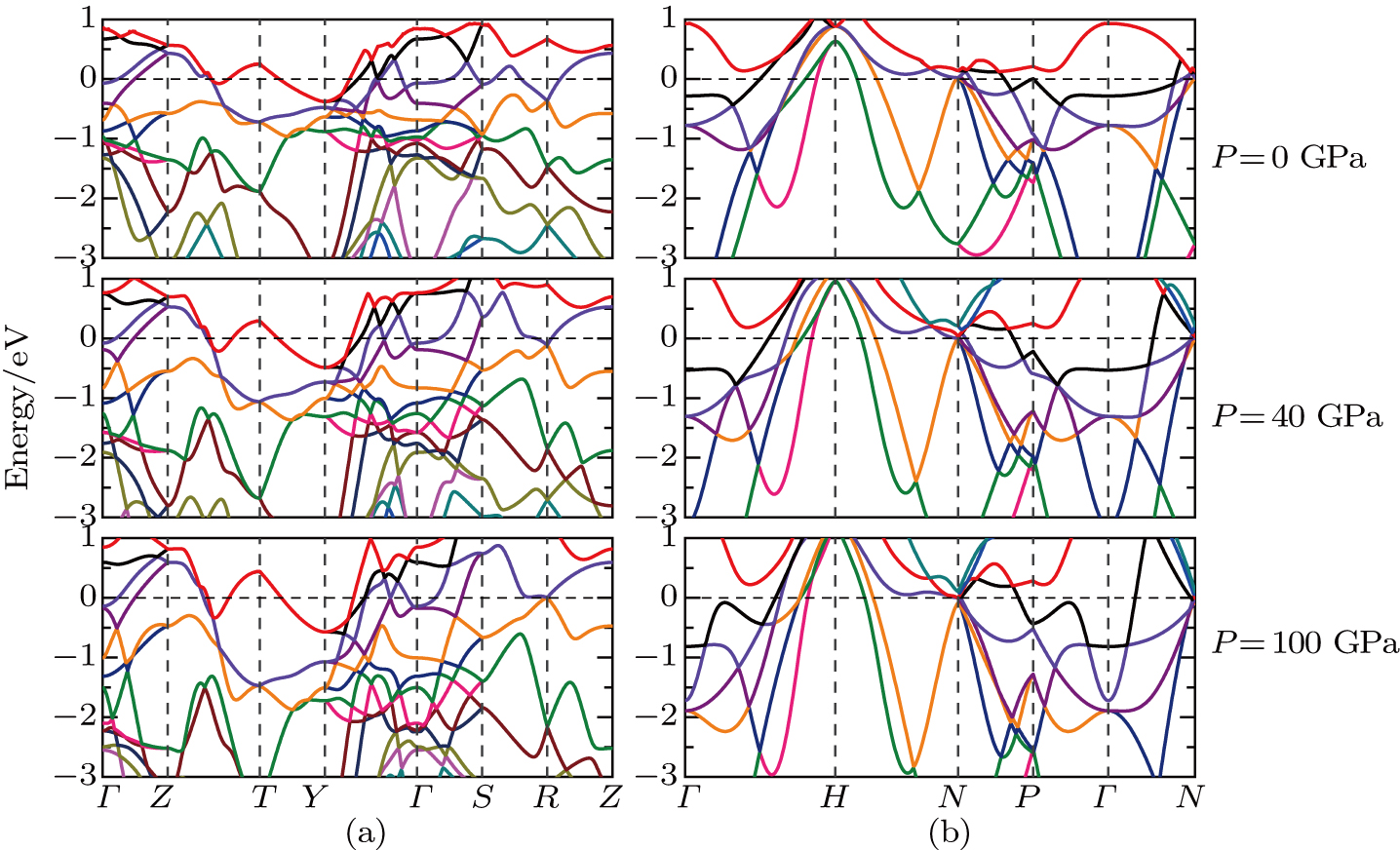
In order to study the effects of pressure on electronic structure, the total and partial density of states (DOSs) of α, β, and γ uranium at 0, 40, 100 GPa are plotted in Fig.
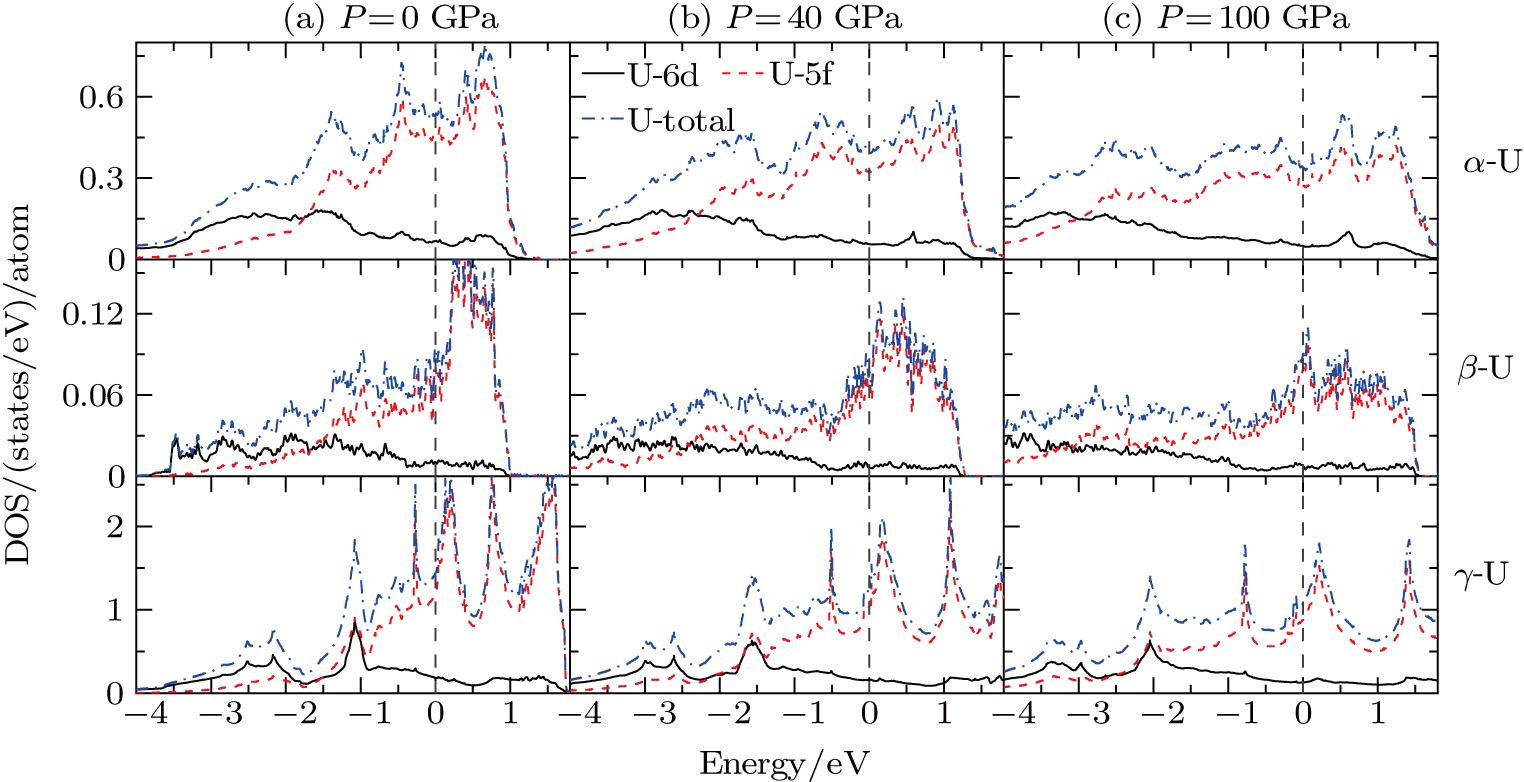 | Fig. 4. (color online) Total and partial densities of states for α, β, and γ phases of uranium at (a) 0 GPa, (b) 40 GPa, and (c) 100 GPa. |
As shown in Fig.
The elastic constants can measure the resistance and mechanical properties of a crystal under external stress, thus describing the stability of crystals against elastic deformation. We present the calculated elastic constants (C11, C22, C33, C44, C55, C66, C12, C13), Poisson’s ratio (ν), elastic wave velocities (υt, υl, υm), and Debye temperature (θD) of α-U in Table
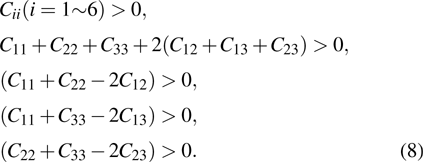 |
| Table 2.
Calculated nine independent elastic constants (C11, C22, C33, C44, C55, C66, C12, C13, C23), Poisson’s ratio (ν), transverse (υt), longitudinal (υl), and average sound velocities (υm) derived from polycrystalline bulk and shear modulus, as well as Debye temperature (θD) of α phase at selected pressures. . |
From the calculated values of Cij, α-U is mechanical stable under pressure up to at least 100 GPa, which is consistent with that of experiments.[12–15] Besides, the nine elastic constants increase almost linearly from 0 GPa to 100 GPa.
For the orthorhombic crystal system, the Voigt bulk modulus (BV) and the Reuss bulk modulus (BR) can be expressed by:
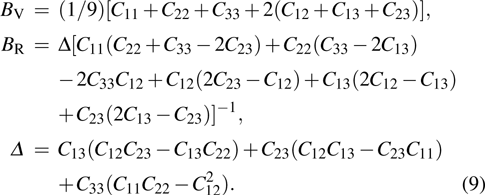 |
The Voigt shear modulus (GV) and the Reuss shear modulus (GR) are defined as:
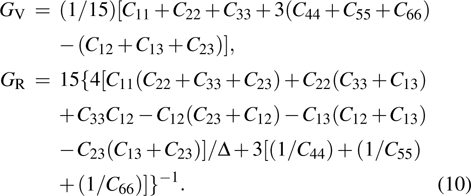 |
Their computational results are plotted in Fig.
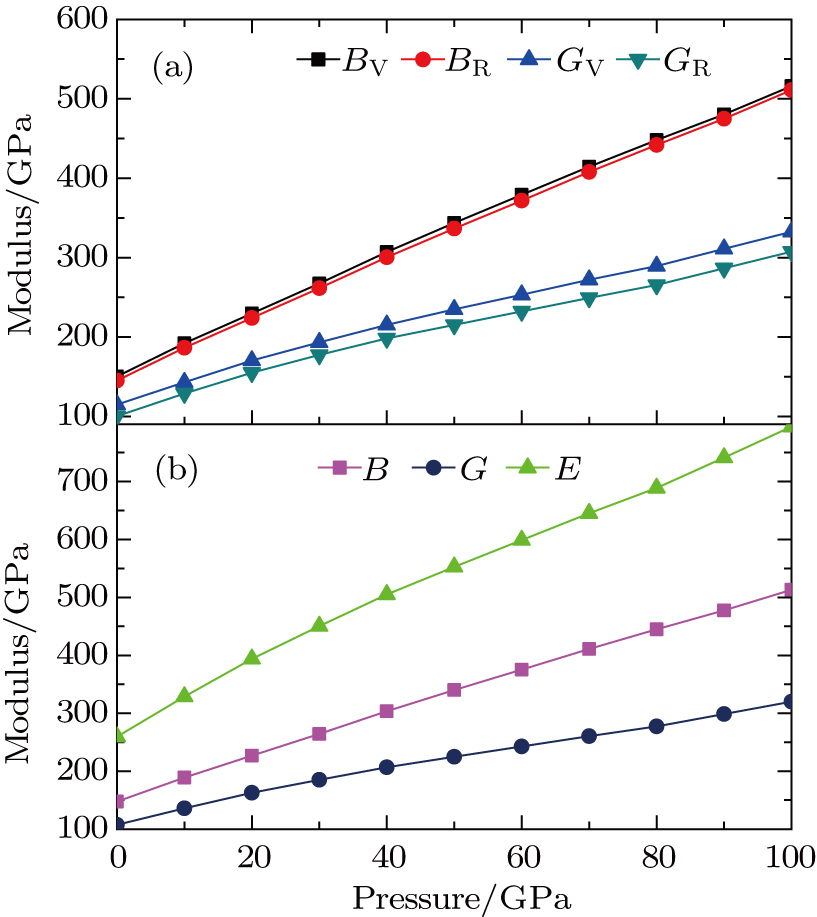 | Fig. 6. (color online) Calculated bulk moduli BV, BR, B, shear moduli GV, GR, G, and Young’s modulus E for α-U as a function of pressure. Solid lines are guides to the eyes. |
In addition, the effects of pressure on elastic moduli, elastic wave velocities, and Debye temperatures are evident. However, the Poisson’s ratio is the most sluggish one upon compression. By using Eqs. (
It is very important to describe the elastic anisotropy behavior in engineering science and crystal physics. Crystal anisotropy reflects atomic arrangements along different directions. The shear anisotropic factors from our elastic constants are showed in Table
| Table 3.
The anisotropic factors for α and β phases. . |
For β-U and γ-U, we list their elastic constants, elastic moduli, elastic wave velocities, and Debey temperature in Table
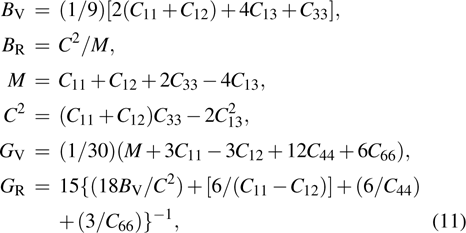 |
| Table 4.
Elastic constants of the β and γ phases of uranium, bulk modulus (B), shear modulus (G), Young’s modulus (E), Poisson’s ratio (ν), transverse (υt), longitudinal (υl), and average sound velocities (υm) derived from polycrystalline properties, as well as Debye temperature (θD) at 0 K. . |
and
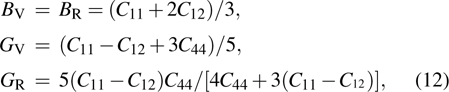 |
respectively. Our calculated elastic constants for β-U are well consistent with the values from Li et al.[28] It is mechanically stable in the ground state because elastic constants satisfy the following mechanically stable criteria[40] of tetragonal structure:
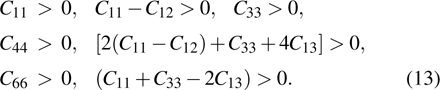 |
In fact, the C12 of β-U is much smaller than C11, the value of B, G, E, and θD decrease from the α phase to the β phase. The obtained bulk modulus value turns out to be accord with the result from the EOS fitting (see Table
Furthermore, there are three elastic anisotropic factors in the tetragonal systems defined as A1 = 2C66/(C11 − C12), A2 = 4C44/(C11 +C33 − 2C13), and A3 = C44/C66. The shear anisotropic factors A1 represents the {001} shear planes while the elastic anisotropic factors A2 for the 
Elastic constants unsatisfy the mechanically stable criteria[40] of cubic structure, so the γ phase is mechanically unstable
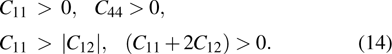 |
The calculations show that C11 is much smaller than C12, which is agreement with other theoretical calculations.[29,32,47]
For bulk modulus, shear modulus, Young’s modulus, Poisson’s ratio, transverse, longitudinal, average sound velocities, as well as Debey temperature of γ are listed in Table
In summary, the structural, electronic, and mechanical properties of the α, β, and γ phases of uranium under pressure up to 100 GPa have been studied by employing the first-principles DFT-GGA method. Our calculations show that the lowest energy structure of U is α-phase (orthorhombic Cmcm-type). By calculating the enthalpies of the three phases, we never find any phase transitions in pressure range of 0 GPa–100 GPa. According to our calculated elastic constants, α and β phases are mechanically stable at ambient pressure. For γ phase, however, it is mechanically unstable at 0 GPa. Under pressure, the bulk modulus B, shear modulus G, and Young’s modulus E increase near linearly for α phase.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] |