† Corresponding author. E-mail:
With the method of replacing the surface layer of photonic crystal with tubes, a novel photonic crystal composite structure used as a tunable surface mode waveguide is designed. The tubes support tunable surface states. The tunable propagation capabilities of the structure are investigated by using the finite-difference time-domain. Simulation results show that the beam transmission distributions of the composite structure are sensitive to the frequency range of incident light and the surface morphology which can be modified by filling the tubes with different organic liquids. By adjusting the filler in tubes, the T-shaped, Y-shaped, and L-shaped propagations can be realized. The property can be applied to the tunable surface mode waveguide. Compared with a traditional single function photonic crystal waveguide, our designed structure not only has a small size, but also is a tunable device.
Photonic crystals have aroused a great deal of interest recently due to their potential ability to control the propagation of light. They possess many unique physical properties. One of the most unique properties is the existence of a photonic crystal bandgap. Many optical devices based on a two-dimensional (2D) photonic crystal with photonic crystal bandgap have been proposed and they are expected to play important roles in future photonic circuits. The waveguide is one of the indispensable components in these devices. By introducing line defects in photonic crystals, a waveguide can be realized, where light is guided along the line defects. These types of photonic crystal waveguides can be called line defect photonic crystal waveguides. A great amount of study has been conducted in designing photonic crystal line defect waveguides, for example, the T-shaped waveguide, Y-shaped waveguide,[1] and L-shaped waveguide.[2]
Another unique feature of photonic crystal is the surface wave. The surface waves are electromagnetic waves localized at the interface between a photonic crystal and another medium. The introduction of line defects along the photonic crystal surface may lead to the occurrence of surface modes which are different from waveguide guided modes. Waveguide guided modes can appear when the photonic crystal has one or more line defects within its lattice. The surface modes at the photonic crystal-air interface are called the uncoupled surface modes. Surface modes may also appear at the interface between two photonic crystals with modified surface. The surface modes at photonic crystal-photonic crystal interface are called the coupled surface modes.[3] These two photonic crystals can be the same or different. The distance between the two modified photonic crystals can be lattice constant or not lattice constant. For a 2D photonic crystal the existence of surface modes has been shown theoretically and experimentally. Many optical devices based on a photonic crystal surface wave have also been proposed.[4] The original surface waves are of the non-radiative mode, which can only propagate strictly along the surface of photonic crystal and cannot couple to the outside space. For that reason, non-radiative surface modes are regarded as an undesirable feature. Most of the previous work has focused on the physics of surface waves and the radiative surface modes. It has been shown that with the help of radiative surface modes it is possible to achieve a directional beam from the waveguide.[5–9] Recently, an approach to waveguide design has suggested the possibility of using non-radiative surface wave on the interface boundary between finite photonic crystal and external,[10–12] so the interest in non-radiative surface waves in photonic crystals arose again.[13–16] The guiding of electromagnetic light waves along the surface boundary of photonic crystal is called photonic crystal surface waveguide.
On the other hand, micro-fluidic devices based on photonic crystals have experienced a significant growth. Many studies have shown the potential application of micro-fluidic devices. For example, Hasek et al. have reported that the sensing of biomaterials is possible in the terahertz region.[17,18] Battula and Chen have reported that a tunable plasmonic-crystal super lens can be designed by using different organic liquids.[19] Chen et al. have reported that a 2D square photonic crystal with the surface modified by tubes can be used to tune beam direction and transmission distribution.[20]
To the best of our knowledge, tunable photonic crystal surface waveguide structures based on composite structure have not been reported so far. In this paper, we propose a novel tunable surface mode waveguide that is based on the non-radiative surface mode. This novel tunable surface mode waveguide structure is a two-photonic-crystal composite structure with the surface modified by tubes. The beam transmission distribution is sensitive to the surface morphology, which can be modified by filling the tubes with different organic liquids. By adjusting the filler in tubes, the T-shaped propagation, Y-shaped propagation, and L-shaped propagation can be realized. Because the transmission distribution is sensitive to the filled liquid, such a kind of structure has an important potential application in integrated optical circuits. It can also be used as micro-fluidic devices to sense micro- and nanoliter volumes of analyte.
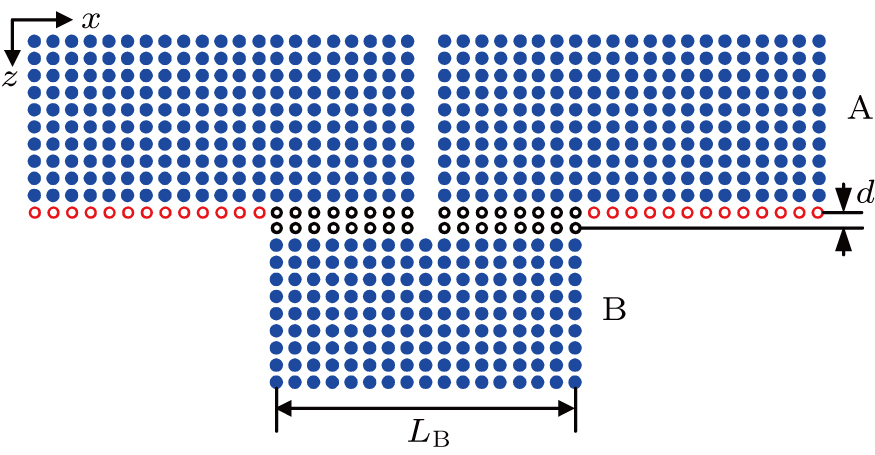
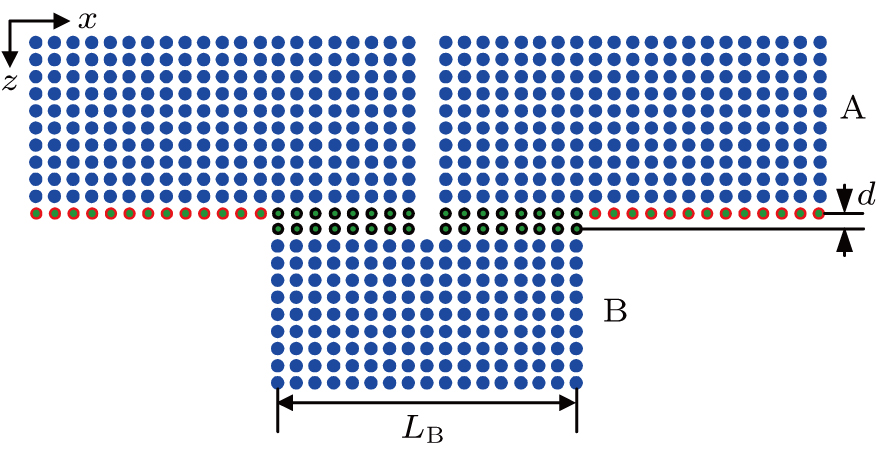
In the present paper, in order to obtain a tunable surface waveguide, we design a novel composition structure as shown in Fig. 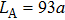
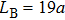
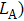

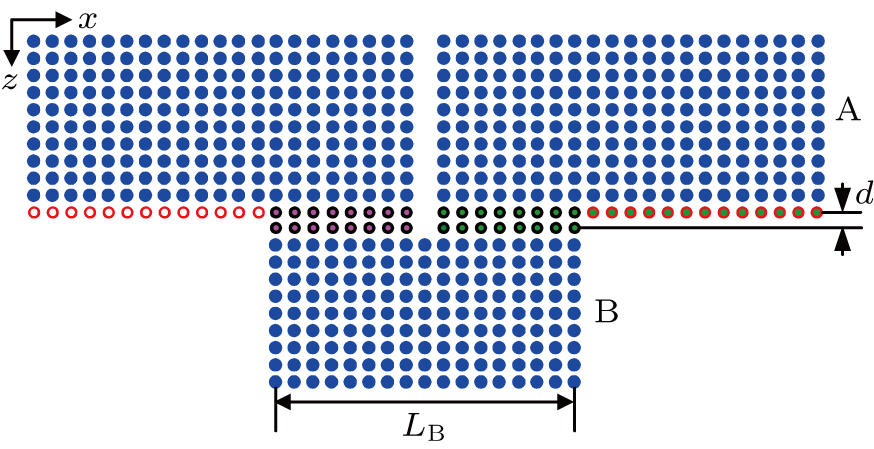
Surface modes can appear at the interface of the photonic crystal-air or photonic crystal-photonic crystal when the surface of photonic crystal is modified. In order to create tunable surface modes, at the input surface of photonic crystal B, the radii of surface cylinders are replaced by the radii of tubes(denoted by black circles) that are made of silicon dioxide (ε = 2.25). The outer radii of these tubes are all 0.16a, and the inner radii 0.1a. At the output surface of photonic crystal A, the radii of surface cylinders are also replaced by the radii of tubes that are madeof silicon dioxide (ε = 2.25). Among these tubes, those tubes (denoted by black circles) that are adjacent to the photonic crystal B each have an outer radius and inner radius 0.16a and 0.1a, respectively. The outer radius and the inner radius of each of the remaining tubes (denoted by red circles) are 0.16a and 0.13a, respectively. These modifications provide the conditions for uncoupled surface modes to exist at the photonic crystal A-air interface and for coupled surface modes to exist at the photonic crystal A-photonic crystal B interface. The distance between the two modified surfaces is d = 0.4a. Photonic crystals A and B constitute a horizontal surface cavity. This horizontal surface cavity is defined as the M cavity, and the length of the M cavity is 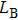
In the composite structure shown in Fig.
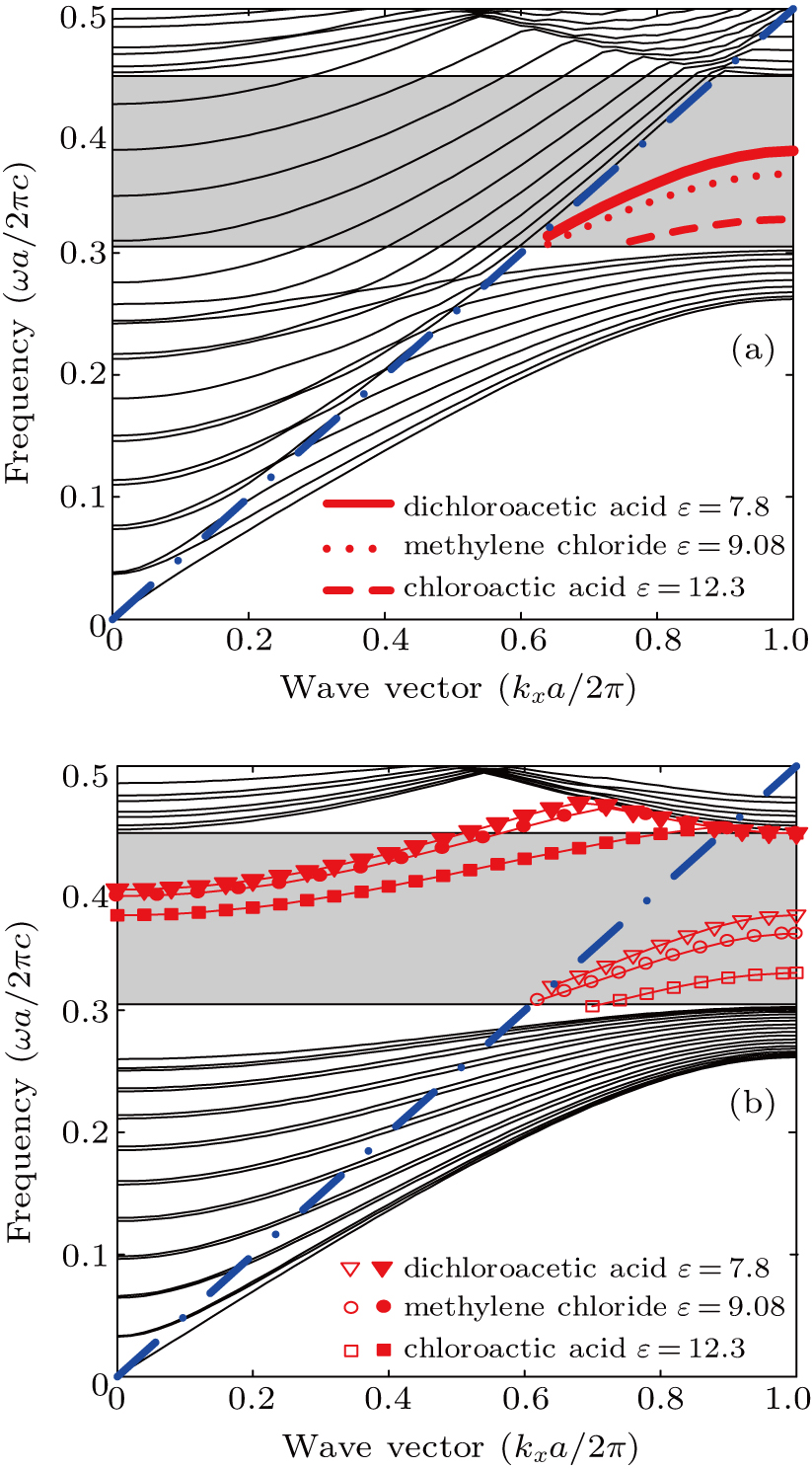
The dispersion relations of uncoupled surface modes (existing at the photonic crystal A-air interface) for surface tubes (denoted by red circles) filled with different organic liquids are calculated, and the results are shown in Fig. 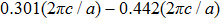
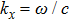
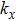
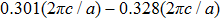

The output surface layer of the photonic crystal A and the input surface layer of the photonic crystal B are modified by a row of tubes. These modifications provide the conditions for coupled surface modes to exist at the interface between photonic crystals A and B. The dispersion relations of coupled surface modes for the surface tubes(denoted by black circles) in the surface layer of the photonic crystal A-photonic crystal B interface, filled with different organic liquids, are calculated, and the results are shown in Fig. 

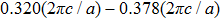
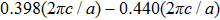
In this section, the tunable propagation capabilities of the structure shown in Fig.
Firstly, in order to obtain T-shaped propagation and Y-shaped propagation, all the surface tubes shown in Fig. 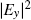
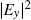
 | Fig. 3. (color online) Schematic diagram of the filled photonic crystal composite structure. All the surface tubes are filled with dichloroacetic acid (ε = 7.8). |
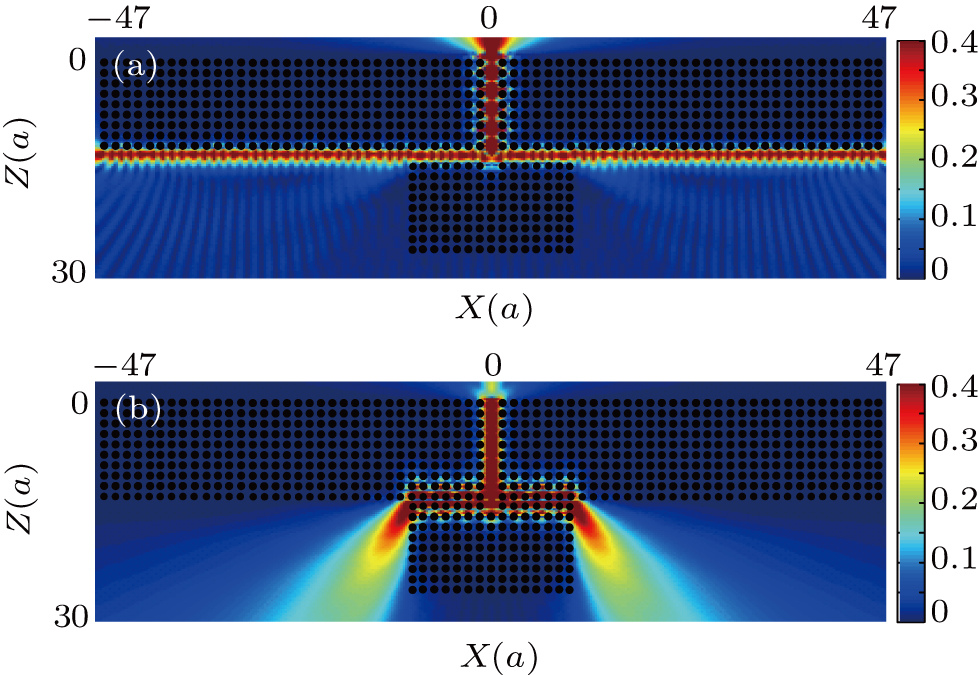 | Fig. 4. (color online) Simulated spatial distributions of 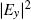
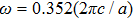
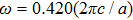
|
Figure 
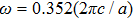
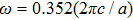

Figure 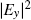

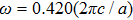
In order to obtain L-shaped propagation, we use different filling methods to fabricate the filled structure as shown in Fig.
Figure 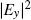

 | Fig. 6. (color online) Simulated spatial distribution of 
|
Figures 
In this paper, a novel tunable surface mode waveguide structure is designed. The designed structure consists of a line photonic crystal waveguide and finite photonic crystal. For this proposed device, its fabrication is similar to that of conventional photonic crystal devices, which can be fabricated by electron-beam lithography technology[23,24] and holographic lithography technology.[25] For practical applications, it is very valuable to experimentally verify the theoretical analysis. The techniques reported in the literature provide the basis for the feasibility of the experiment. It is our future work to verify the theoretical analysis experimentally.
In this work, we design a new tunable surface waveguide by the method of replacing the surface layer of composite photonic crystal structure with tubes. Using the FDTD method, we obtain the field pattern for several filling forms of the photonic crystal structures. The simulation results show that beam patterns depend on the frequency of incident light and the materials which are filled in surface tubes. The T-shaped propagation and Y-shaped propagation emerge when all the surface tubes are filled with dichloroacetic acid. L-shaped propagation can be realized if the tubes are filled with different fluids in the left and right side of the z axis. The property can be applied to tunable surface waveguide. Compared with a traditional single function photonic crystal waveguide, our design structure not only has a small size, but also is a multifunctional device.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] |