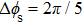† Corresponding author. E-mail:
We investigate theoretically and numerically the evolutions of optical pulses in the time domain due to modulation instability (MI), where CW pump accompanied with a probe is used as the input of nonlinear fiber. As the fiber length increases, we show that it exhibits beat frequency between the pump and the probe first when the probe lies outside the MI resonance region, and then gradually transforms into a pulse train resulting from spontaneous MI rather than induced MI. However, the regular pulse train is easier to generate in the whole fiber if the probe exists in MI resonance region, and the period of the pulse train is inversely proportional to the frequency spacing between the pump and the probe. It is emphasized that the pulse period can be adjusted only when the probe is in MI resonance region. The numerical simulations are in agreement with the theoretical results. The obtained results are guidable for generating and manipulating the optical pulse train in the fiber.
Modulation instability (MI) is a significant nonlinear effect in optical fiber, which is caused by the interaction between fiber dispersion and nonlinearity.[1–3] In the frequency domain, MI manifests itself as two symmetric spectral sidelobes, while it splits into a short-pulse train in the time domain for CW or quasi-CW. As is well known, MI can be divided into spontaneous MI and induced MI, which result from the background noise and the probe light, respectively.[1] For the latter, it has been widely accepted that the period of the generated pulses is inversely proportional to the frequency spacing between the pump and the probe, since it was first reported by Tai et al. in 1986.[4,5] It means that the period of pulses can be manipulated by changing the position of the probe in the input spectrum based on induced MI. However, in the authors’ opinion, the above conclusion should be limited to the condition that the probe exists within the region of spectral sidelobes caused by spontaneous MI, which corresponds to the so-called MI resonance.[6] In the MI resonance region, the efficiency of four-wave mixing (FWM) induced by MI is highly improved,[7–9] and a frequency comb structure always occurs. On the contrary, if the probe lies out of MI resonance region, the performance of the generated pulse train will become rather different, and this will be investigated in detail in the present paper.
The aim of this paper is to investigate different characteristics of pulse evolution when the probe is in and outside the MI resonance region, respectively. The CW pump and high nonlinear fiber are used. It is supposed that the bandwidth of the pump is broad enough for stimulated Brillouin scattering (SBS) not to occur. Stimulated Raman scattering (SRS) is also absent if the pump power is lower than its threshold. To be noticed, the performance of generated pulses changes when SRS is considered, which is not the task of this paper but well presented in Ref. [10].
The CW pump accompanied by a probe is used as an input. It can be divided into two cases, i.e., the probe lies in and outside the MI resonance region of the pump. The two different cases will first be investigated theoretically in the following.
At the beginning of the fiber, there are only the pump and the probe in the spectrum. However, as fiber length increases, spontaneous MI occurs with two symmetric spectral sidelobes. The maxima of the sidelobes correspond to the first-order MI frequency peaks. Then the second-order MI frequency peaks emerge due to the FWM effects between the first-order frequency peaks and the pump. There are similar processes for higher-order MI frequency peaks. Finally, a frequency comb structure is present composed of different orders of frequency peaks, which has been found experimentally in our former researches.[11] To be noticed, these MI frequency peaks resulting from FWM processes satisfy phase-matching condition precisely.[1] Moreover, the power of higher-order peaks is lower than that of lower-order ones. To simplify the model and obtain an analytical expression, it is supposed that the power decrease between adjacent frequency peaks is the same. This hypothesis will not change the variation trend of the results, in our opinion, because the difference between the real case and the supposed one only exists in the exact value of the power of different-order peaks. The reasonableness of this hypothesis can also be confirmed by the simulation results of the generalized nonlinear Schrödinger equation in the next section. Therefore, at a given fiber length, the complete electric field can be expressed as
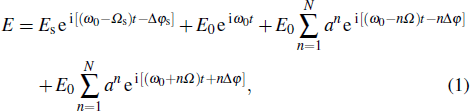 |
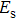
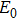
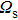
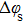
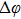
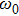
In the front section of the fiber, the MI effect is so weak that it can be ignored, leaving only the pump and the probe. Therefore, the complete electric field in Eq. (
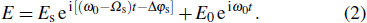 |
Using Eq. (
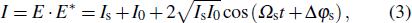 |
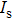
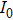
However, in the back section of the fiber, MI becomes so strong that different orders of frequency peaks occur simultaneously with their phases matched. As a result, the comb-like structure resulting from MI has a dominant effect if the probe is weak enough. Thus the influence of the probe can be excluded and the corresponding electric field can be expressed as
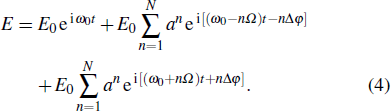 |
The above expression can be further derived as (see Appendix
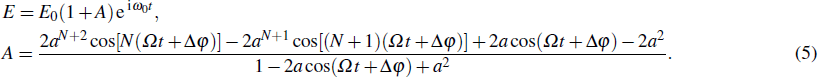 |
Using Eq. (
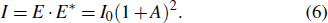 |
Furthermore, for the middle section of the fiber, both the frequency comb and the probe should be considered, and the electric field can be expressed as
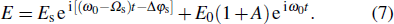 |
Using Eq. (
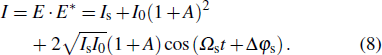 |
Based on Eqs. (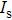
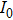
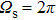

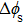

Figure 
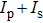
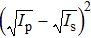
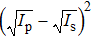
Figure 
On the contrary, when the probe lies in MI resonance region, MI-induced FWM becomes significant, leading to the occurrence of frequency-comb-like structure. It corresponds to the case expressed by Eq. (
As is well known, the generalized nonlinear Schrödinger equation can be used to numerically simulate optical transmission in the fiber,[1] and it can be expressed as
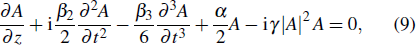 |
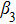
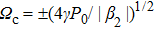
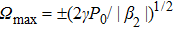
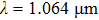
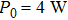
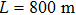
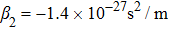
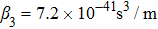
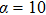
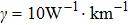
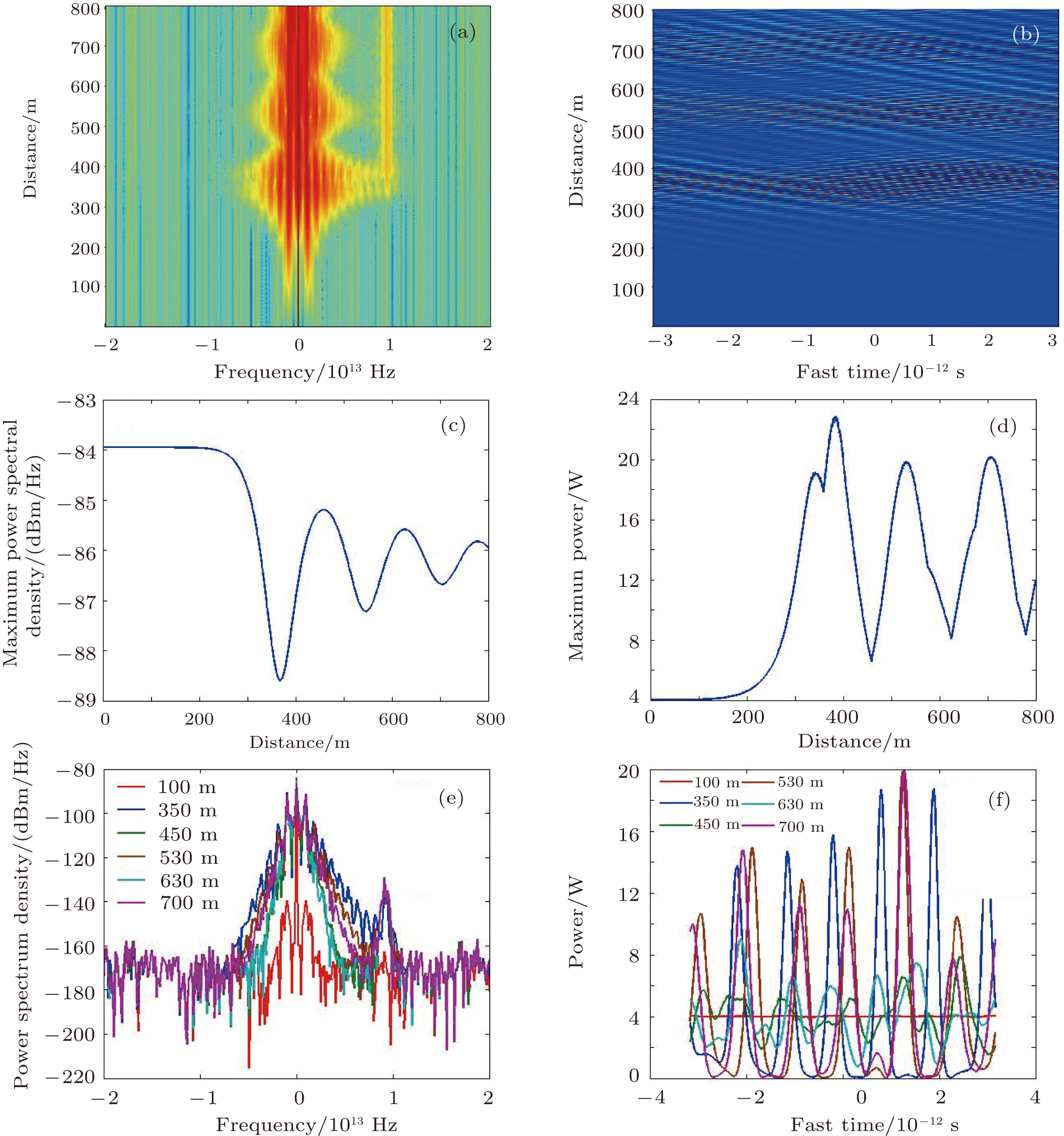
To be clear, the case without a probe serving as the input is investigated primarily. Figure 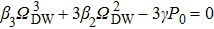
To get a better insight, the maximum evolutions of frequency and time domain with fiber length are shown in Figs.
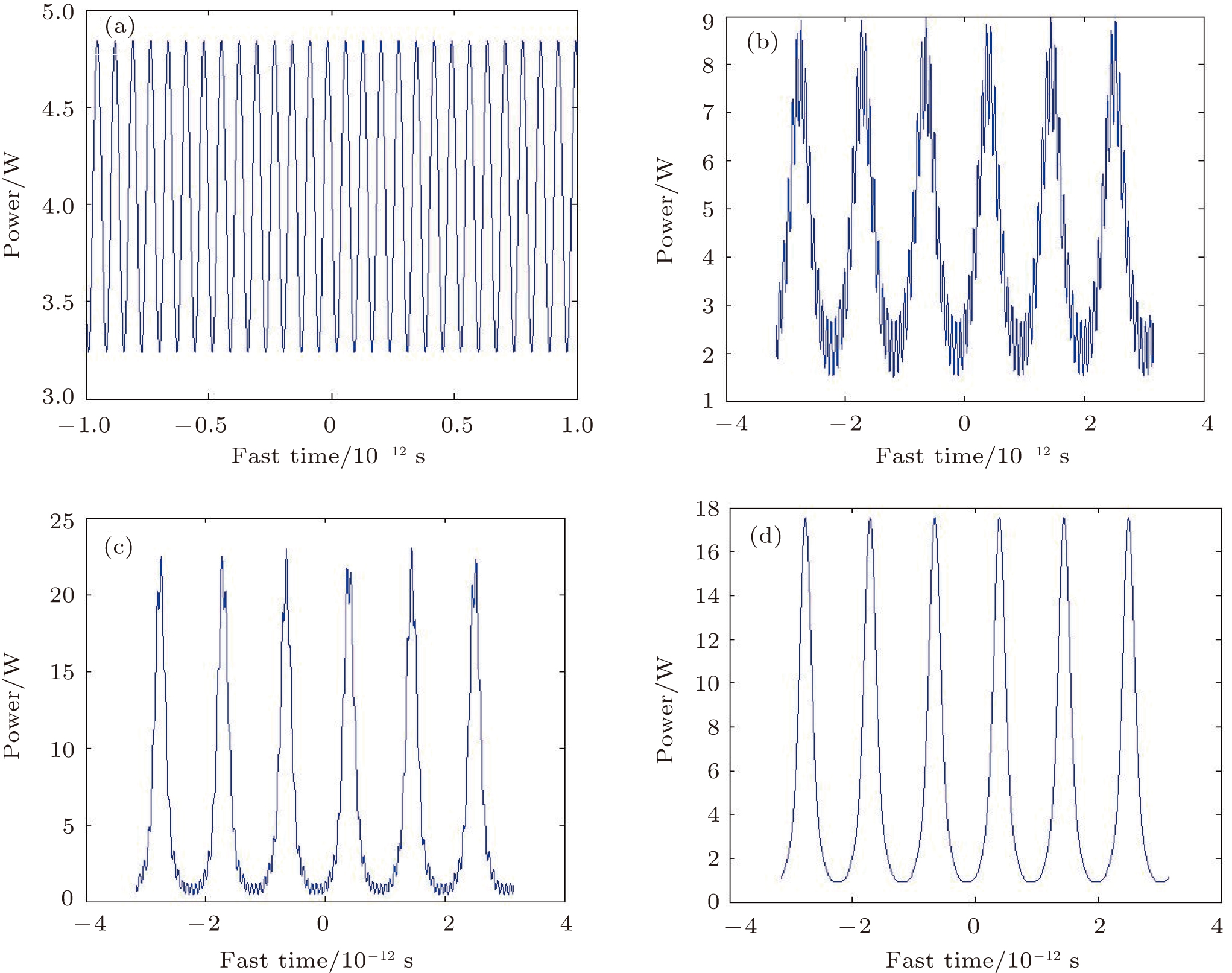
As mentioned in the theory section, the waveform first manifests itself as a pump-probe beat when the pump is accompanied by a probe outside the MI resonance region as the input, corresponding to the beginning part of the fiber. With the increase of fiber length, MI becomes significant gradually and the waveform evolves to the pulse shape. To confirm this, a probe with a power of 40 mW and a frequency spacing of 13.86 THz is used in the simulation and the results are shown in Fig.
Figures
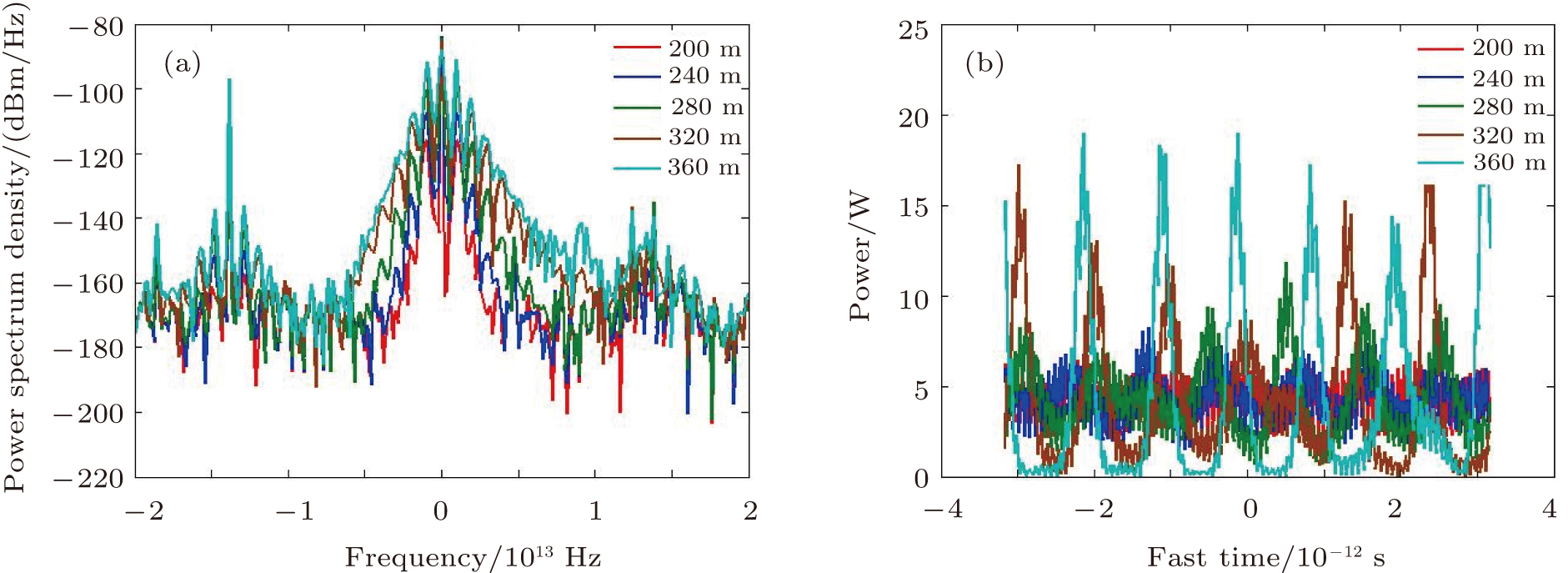
Moreover, the probe power is changed to 200 mW, with its frequency spacing unchanged. The corresponding spectra and time-domain waveforms at the positions of 200 m, 240 m, 280 m, 320 m, and 360 m are shown in Figs.
The case with a probe outside the MI resonance region has been presented, and the other case with the probe in MI resonance region will be investigated in detail hereafter, which is quite different from the above results. The frequency spacing of the probe is changed to 1.26 THz with the power of 40 mW. As mentioned above, the MI resonance region of the pump with considering the effect of fiber attenuation is between zero and ∼ ±1.6 THz, so the probe lies in MI resonance region. Figures
As is well known, MI has been used to generate ultra-short pulses. From the above analysis, there are some points that one should pay attention to. First, in the absence of the probe, the pulse train appears after propagating through a certain fiber span, and the pulses become regular and distorted alternately due to the phenomenon of FPU recurrence. Second, when the probe lies outside the MI resonance region, the beat between the pump and the probe and the pulse train resulting from spontaneous MI emerge one after another with a transition region in between. The probe power also has an influence on this transition region. Third, when the probe lies in MI resonance region, the pulse train is much easier to occur with more regular pulse shape because of MI induced FWM, and the period of the pulses equals the reciprocal of the frequency spacing between the pump and the probe.
The above results are extremely guidable for the practical applications of pulse train manipulations. Primarily, the period of the generated pulse train depends on the position of the probe in the spectrum. When the probe lies outside the MI resonance region, the period corresponds to the reciprocal of frequency spacing of spontaneous MI, while it is inversely proportional to the frequency spacing between the pump and the probe only when the probe lies in MI resonance region. Thus the probe must be located in MI resonance region to realize the adjustment of the pulse train period. In addition, FPU recurrence is always present and its period differs when the probe lies in and outside the MI resonance region. The special positions with fewer frequency peaks should be excluded where the generated pulses are distorted.
In this paper, the evolution of optical pulse in nonlinear fiber has been investigated theoretically and numerically with a pump and a probe serving as the input. It can be divided into two cases, i.e., the probe lies - outside the and in MI resonance region. For the former case, it is found that the time-domain waveform transits from the pump-probe beat to the pulse train gradually. The period of the pulse train equals the reciprocal of the frequency spacing of spontaneous MI rather than the spacing between the pump and the probe. For the latter case, it is found that the regular pulse train is easier to occur with its period corresponding to the reciprocal of the frequency spacing between the pump and the probe instead. Thus the period of the generated pulse train can be adjusted by changing the pump-probe frequency spacing only when the probe lies in MI resonance region. The results obtained by numerical simulations accord well with the theoretical results.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] |