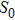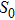† Corresponding author. E-mail:
Cascaded fiber geometry with the dispersion of each fiber decreasing is proposed to enhance the multiple four-wave mixing (FWM) generation. The first fiber with relatively large dispersion initiates and accelerates the expansion of multiple FWM, and the second fiber with small dispersion would allow the phase-matching process (thus the spectrum broadening) to keep going. Numerical and experimental results show that with this geometry not only multiple FWM expansion can be accelerated, but also the efficiency of multiple FWM products can be effectively improved with shorter fibers.
Multiple four-wave-mixing (FWM), also named cascaded FWM, in optical fibers has been demonstrated to be a promising way to achieve boradband optical frequency comb (OFC).[1–5] Compared with the cavity-defined approaches, such as mode-locked fiber lasers[6,7] and microresonator,[8] OFC based on multiple FWM is convenient to easily tune the frequency spacing, and is free from frequency chirps and pulse jitter inherently.[3] It has been proposed to serve as high precision frequency markers, calibration of astrophysical spectrometers, broadband spectroscopy and metrology.[2,9] Multiple FWM can also find its applications in high repetetion-rate, short-pulse source,[10] and wavelength division multiplexing systems.[11,12]
Some techniques have been proposed to enhance the multiple FWM, e.g., using triple pumps with unequally spaced frequencies,[13] adding an optical feedback into the nonlinear fiber.[14] Discrete dispersion-increasing fibers were cascaded to extend the multiple FWM spectrum, and the efficiency of multiple FWM products at shorter wavelengths has been effectively improved.[1] In addition, multistage mixers with synthesized dispersion were demonstrated to generate wideband OFC.[3]
As is well known, FWM in long fiber will degrade the performance of FWM generation. In this case, fiber random birefringence and undesirable variation of the zero dispersion wavelengths (ZDWs) along the fiber will reduce the efficiency of multiple FWM.[15] Furthermore, sophisticated technologies have to be adopted to counteract the low-threshold stimulated Brillouin scattering (SBS)[16] in the long fibers. So short fibers with high nonlinearity, such as highly nonlinear fibers (HNLFs)[17] and photonic crystal fibers,[1] are ideal to generate broadband multiple FWM products.
Here, we propose a cascaded-fiber geometry where the dispersion of each fiber decreases on wave propagation. The first fiber with relatively large dispersion initiates and accelerates the expansion of multiple FWM, and the second fiber with small dispersion would allow the phase-matching process to keep going, thus broadening the output spectrum. The proposed scheme is demonstrated numerically and experimentally, which shows that with this geometry the multiple FWM expansion can be accelerated, and the efficiency of multiple FWM products can be effectively improved with shorter fibers.
To demonstrate the proposed cascaded fiber geometry with discrete dispersion-decreasing fibers, numerical simulations of multiple FWM in two fibers with the same ZDW but different dispersion slopes are carried out first. FWM in optical fibers is conventionally modeled with coupled amplitude equations.[18] However, for multiple FWM generation with hundreds of FWM products to be considered, the nonlinear Schrödinger equation should be used[1,18]
 |
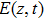
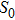

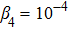
Two continuous-wave (CW) seeds at 1555 nm and 1563 nm with the same power of 10 W are injected into the fiber. In order to model the parametric amplification of quantum noise, a white-Gaussian noise,[1,14] with optical signal-to-noise ratio (SNR) of 120 dB at 12.5 GHz, is added to the input seeds. Even though the noise can be set to be zero in the numerical simulations, the bandwidth of multiple FWM will be limited by the phase mismatch. The detailed theory of FWM can be found in Ref. [1] and Chapter 10 of Ref. [18].
Two sections of 10 m fibers with 
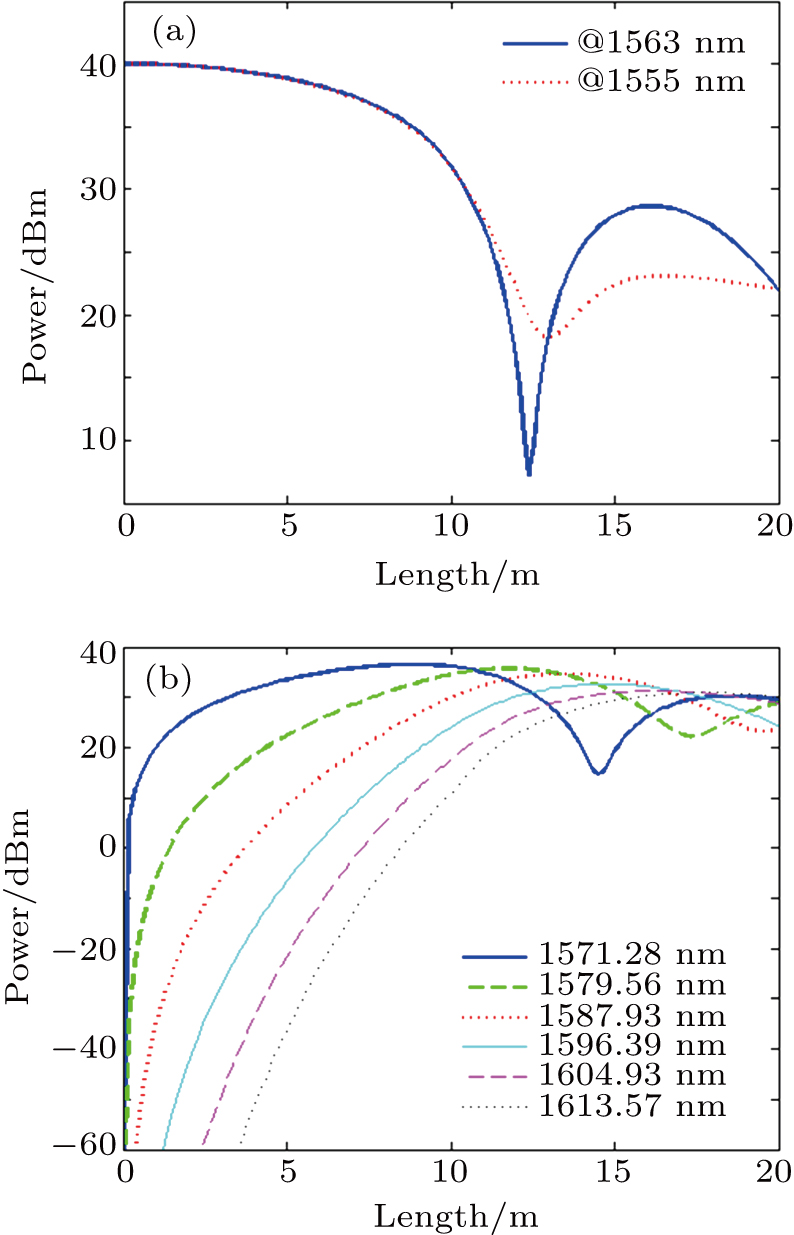 | Fig. 1. (color online) Power evolutions along the fiber for (a) pumps, and (b) generated multiple FWM products at the first six idler wavelengths. |
To show the accelerated expansion of multiple FWM products in the cascaded fibers with discrete dispersion decreasing, spectrum evolutions in different fiber geometries are shown in Fig. 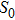

However, if the two fibers are interchanged, i.e., fibers are cascaded with dispersion increasing, the final output spectrum is not so broad, which is shown in Fig. 

As seen above, the comb expands quicker in the fibers with larger dispersion. To achieve a maximum parametric gain, the effective phase mismatch 



Once broad FWM products have been achieved in fibers with large dispersion, further propagation in fibers with small dispersion will drive the energy flow to outer sidebands continuously. As shown in Fig.
As mentioned above, appropriate lengths of the cascaded fibers are critical for generating the comb efficiently. Once power reversion happens between generated products, the comb generation becomes complex. In Ref. [1], the number of FWM products with acceptable SNR is found to drop after the optimal length has been reached, which can be explained with the spectrum dynamics in Fig.
To further verify the proposed scheme, preliminary experiments of multiple FWM are carried out with the setup shown in Fig. 

| Table 1.
Numbers of multiple FWM products with SNR higher than 20 dB, bandwidth and conversion efficiency in the four cases in Fig. |
 | Fig. 4. Simulation of the multiple FWM generation along fiber A, with the same parameters of inputs as those in the experiments. |
 | Fig. 5. Output spectra of multiple FWM generated in (a) 94-m-long fiber A plus 106-m-long fiber B, (b) 106-m-long fiber B plus 94-m-long fiber A, (c) 200-m-long fiber A, and (d) 200-m-long fiber B. |
The spectrum of multiple FWM expands faster in fiber with larger dispersion, but the power reverts back from sidebands to pumps after a certain fiber length, which leads to the reduction of conversion efficiency. While parametric gain bandwidth is broader in fibers with smaller dispersion,[17] which is consistent with the result of a comparison between Figs.
Therefore, in order to enhance the efficiency of multiple FWM, broaden the bandwidth and increase the power of the components, the principle of dipersion decreasing should be maintained. To optimize the fiber geometry of multiple FWM, the appropriate lengths of fiber under different dispersions and pumping powers should be estimated and employed to make sure the pump power keeps flowing to the sidebands.
Accelerating expansion of multiple FWM products is proposed and demonstrated in a cascaded fiber geometry with discrete dispersion-decreasing fibers. Simulations and experiments demonstrate that this geometry can accelerate the multiple FWM expansion, thereby effectively improving the efficiency of multiple FWM products with shorter fibers.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] |