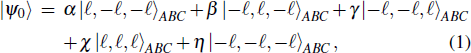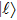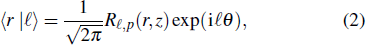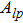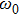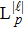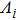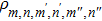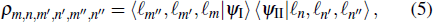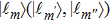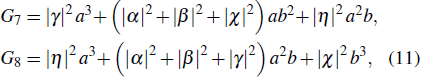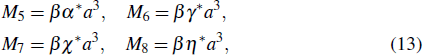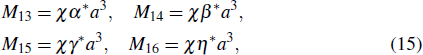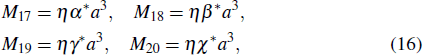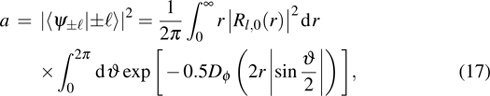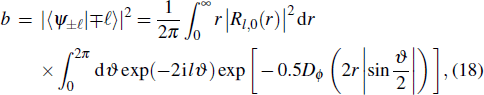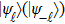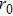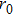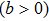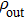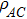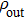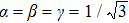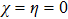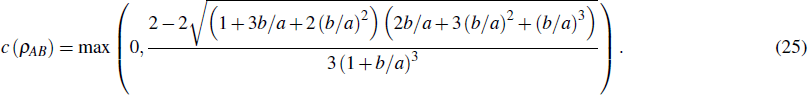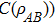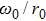Cite this Article
Yan Xiang, Zhang Peng-Fei, Zhang Jing-Hui, Feng Xiao-Xing, Qiao Chun-Hong, Fan Cheng-Yu. Effect of atmospheric turbulence on entangled orbital angular momentum three-qubit state . Chinese Physics B, 2017, 26(6): 064202  
Permissions
Effect of atmospheric turbulence on entangled orbital angular momentum three-qubit state
Yan Xiang1, 2, Zhang Peng-Fei1, Zhang Jing-Hui1, Feng Xiao-Xing1, Qiao Chun-Hong1, Fan Cheng-Yu1, †
Key Laboratory of Atmospheric Composition and Optical Radiation, Anhui Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Hefei 230031, China
University of Science and Technology of China, Hefei 230026, China

 

† Corresponding author. E-mail: cyfan@aiofm.ac.cn

Abstract

The entangled orbital angular momentum (OAM) three photons propagating in Kolmogorov weak turbulence are investigated. Here, the single phase screen model is used to study the entanglement evolution of OAM photons. The results indicate that the entangled OAM three-qubit state with higher OAM modes will be more robust against turbulence. Furthermore, it is found that the entangled OAM three-qubit state has a higher overall transmission for small OAM values.

PACS: 42.50.Ar;03.67.Mn;03.65.Ud
Keyword:three-qubit state;turbulence atmosphere;Kolmogorov turbulence
1. Introduction

Quantum entanglement is an important concept in quantum mechanics. It is a key ingredient in the field of quantum information processing (QIP), such as quantum teleportation, quantum key distribution (QKD), and quantum secure direct communication (QSDC).[1–7]

Recently, the orbital angular momentum (OAM) has been intensively investigated, because the use of OAM modes of light to encode quantum in a high-dimensional Hilbert space could provide many advantages, among which the increased alphabet size for information transmission is a main merit. This interesting property can allow the significant increase of the transmission rate and the improvement of the security in quantum key distribution.[8–12] However, when the entangled OAM photons propagate through atmospheric turbulence, OAM modes may suffer distortions due to the scintillation process. This inevitably causes the decay of OAM entanglement, which is the primary limitation to the realization of OAM-based quantum communication. Although many efforts have been made to effectively reduce and mitigate the influences of atmospheric turbulence on OAM photons,[13–24] the description of the OAM entanglement evolution is still a fundamental open issue.[13–29] It is necessary and important to find a suitable way to quantify the OAM entanglement evolution in turbulence.[27]

Until now, there have been many theoretical and experimental studies devoted to the influence of atmospheric turbulence on the OAM photons.[13–31] However, as far as we known, the OAM of a single photon and entangled pairs of photons have been studied widely, but the entangled OAM three photons have not been reported yet. In this paper, we further investigate the evolution of OAM-entanglement among three qutrits in weak turbulence, whose effect on the propagating optical beam is reduced to phase aberrations. Here the quantum entanglement is quantified by the square of the concurrence.[32] Additionally, the channel fidelity of the output state relative to the input state is also considered. The rest of this paper is organized as follows. In Section 2 the influence of Kolmogorov turbulence on the entangled OAM three-qubit state is presented. In Section 3 the numerical results and analysis are provided. Finally, a brief discussion and some conclusions are given in Section 4.

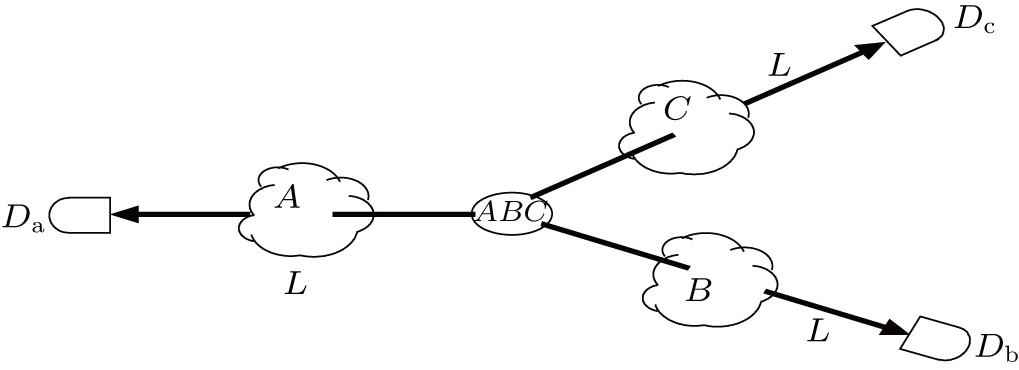
2. Influence of Kolmogorov turbulence on the entangled OAM three-qubit state

A diagram of our setup is shown in Fig. 1. Assume that the initial three-qubit state is encoded by Laguerre–Gaussian (LG) modes

where , the subscripts A, B, and C denote three photons, and are OAM eigenstates (LG modes), and the parameter ℓ is the azimuthal mode order. In normalized cylindrical coordinates, the LG modes are expressed as[23]
where , θ is the azimuthal angle, the parameter p is the radial quantum number, and is the Laguerre–Gauss function. Throughout this paper we use
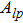
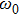
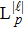
where is a normalization constant, is the beam waist radius, and represents the generalized Laguerre polynomials. In the present study, the zero radial quantum number p = 0 and the azimuthal modes of are only considered.

Fig. 1. Sketch of the setup. The entangled OAM three-qubit state whose wave front is deteriorated as it propagates through independent weak turbulences along the plane z toward a detector. Each atmosphere, labeled by A, B, and C, is assumed to have the same statistical properties (Fried parameter ). The propagation distance for each photon is L.

As the entangled OAM three photons are sent through uncorrelated dissipative channels, the random refractive index fluctuations introduce the phase aberrations that cause the OAM modes of each photon to scatter into neighboring OAM modes. This scattering process eventually destroys the OAM entanglement. Generally, to know the evolved state after turbulence, the density matrix is required. It is given by

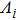
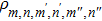
where is the density matrix of the initial state, is the linear map which represents the action of an ensemble averaged phase screen on each photon,[30] is the density matrix element at the output of the turbulence, given by
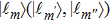
where the basis element denoted by and ( can be explained as the states at the measurement stage. The state is the initial state after propagating through turbulence. The turbulence is assumed to be in the weak regime, where the cumulative effect of the turbulence is reduced to phase errors in the transverse profile. This allows us to express the state in cylindrical coordinates as
where is the random phase perturbation of each turbulence.

Note that owing to the random refractive index fluctuations in turbulent atmosphere, any particular OAM state of the photon is scattered into the infinite-dimensional OAM space.[14,20,23,25,27,28] However, after OAM photons passage through the turbulence, the information contained in the finite OAM subspace can be extracted in the measurement process. For this reason the multilevel state of each photon has been post-selected onto a two-level state ( .[14,18] That is, any perturbation takes the OAM outside of the subspace resulting in a loss. Furthermore, each atmosphere is assumed to have the same coherence length 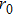(Fried parameter), where ,[33] 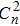is called the atmospheric refractive index structure constant which describes the strength of turbulence along the path, L is the propagation distance, and λ is the wavelength. With the above assumption, the resulting density matrix can now be written as

where
a being the survival amplitude, b being the crosstalk amplitude, and[30]
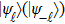
here being the phase structure function of the Kolmogorov model of turbulence.[33] The state is the OAM of single photon state after interaction with turbulence, is the radial part of the input LG beam at z = 0, with radial quantum number and the azimuthal mode order ℓ.

Equation (7) is the main result of this paper. It shows that when the Fried parameter 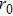tends to infinity, which corresponds to the absence of turbulence, the survival amplitude is equal to 1, and the crosstalk amplitude is 0. On the other hand, when the Fried parameter 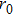is in finite values, the beam distortions in turbulence cause the photon to scatter into many OAM states. That is to say, there emerges a nonzero crosstalk 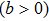, which leads to loss of entanglement.[30]

Finally, the truncated density matrix is normalized and the entanglement evolution of the OAM three-qubit state is examined through calculating the squared concurrence of each qubit with the rest of the system (i.e., , which is the minimum of the average of squared concurrence between qubit A and the pair BC over all decompositions 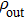. It gives a lower bound for mixed quantum state and can be written as[32]

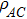
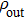
where and are the reduced density matrices obtained from the output density matrix by tracing over qubit C and qubit B, respective, is an essential three-way entanglement of the triple that represents a collective property of the three qubits. Similarly, one can also obtain

In order to better understand the above results, we discuss a special case in which the initial state is the W state, corresponding to 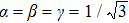, 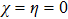. After very tedious calculations, the following results can be obtained:

One can find that three qubits are entangled with each other for the W state, even though the essential three-way entanglement of the triple 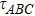is always zero. In addition, the survival amplitude gradually decreases in turbulence and results in b/a monotonic growth until all concurrences vanish (b/a ≈ 0.2144), corresponding to separable state.

3. Numerical results and analysis

In this section, the influence of turbulence on entangled OAM three photons is calculated according to Eqs. (23)–(25). The results are presented in Figs. 2 and 3.

Fig. 2. (color online) Concurrences of each pair of qubits (i.e., as a function of the ratio for different magnitudes of the initial azimuthal modes.
Fig. 3. (color online) Squared concurrences of each qubit with the rest of the system (i.e., as a function of the ratio for different magnitudes of the initial azimuthal modes.

Figure 2 shows the concurrence of each pair of qubits (i.e., 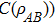plotted against the ratio 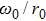for different values of the initial azimuthal modes. One finds from Fig. 2 that the concurrence gradually decreases as OAM photons propagate through turbulence, but the entangled OAM photons with the larger azimuthal modes have a better performance than those with smaller azimuthal modes. This can be understood as follows. With the azimuthal mode increasing, its phase front oscillates more rapidly, and thus its spatial phase structure turns finer.[27,30]

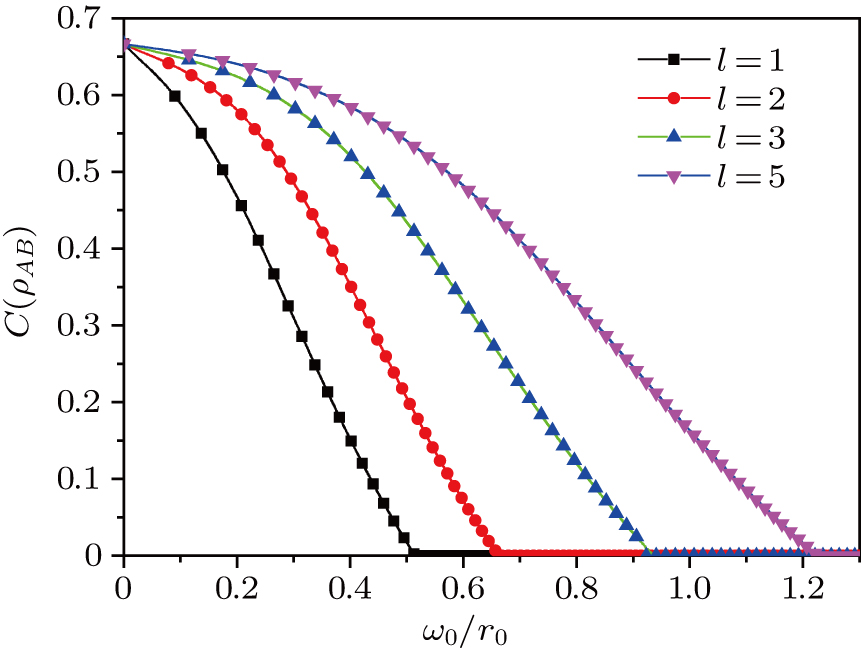
In Fig. 3, the squared concurrences of each qubit with the rest of the system (i.e., are plotted against the ratio for different values of the azimuthal modes. It is clear that the squared concurrence decays through Kolmogorov turbulence. However, the entanglement can survive longer for larger values of the azimuthal index ℓ, which means that the entangled OAM three photons with the larger azimuthal modes are more robust against atmospheric decoherence.

In our simulation, the channel fidelity of the output state relative to the input state is also considered, which is given by[17]

The result is shown in Fig. 4. It is deduced from Fig. 4 that the channel fidelity rapidly decays as the ratio increases. The decay is so fast with the increase of the azimuthal modes, thus indicating less influence of turbulence on the overall transmission of the OAM state with small OAM modes, as observed in Ref. [17].

Fig. 4. (color online) Behaviors of channel fidelity as a function of ratio for different magnitudes of the initial azimuthal modes.

It can further be shown that if three photons are initially in the Greenberger–Horne–Zeilinger (GHZ) state ( , , all the pairwise concurrences are zero ( , and the squared concurrence of each qubit with the rest of the system is . Similar curves are obtained for the GHZ state, leading to the same conclusion.

4. Discussion and conclusions

In this paper, we theoretically investigate the entanglement evolution of OAM three-qubit state propagating in Kolmogorov weak turbulence. Here, the case in which all photons are sent through turbulence is considered. The entanglement evolution of the OAM three-qubit state is quantified by the squared concurrence of each qubit with the rest of the system. Additionally, the channel fidelity of the output state relative to the input state is also studied. The results show that OAM entanglement decays through Kolmogorov turbulence, but the entangled OAM three-qubit state with larger azimuthal modes is more robust against atmospheric decoherence. Moreover, it is found that the entangled OAM three-qubit state with small OAM modes has a higher overall transmission in turbulent atmosphere, which accords well with the case of two photons.

Reference
[1] Jeong H Kim M S 2002 Phys. Rev. 65 042305
[2] Ralph T C Gilchrist A Milburn G J 2003 Phys. Rev. 68 042319
[3] Van Enk S J Hirota O 2001 Phys. Rev. 64 022313
[4] Jeong H Kim M S Lee J 2001 Phys. Rev. 64 052308
[5] Gottesman D Preskill J 2001 Phys. Rev. 63 022309
[6] Cerf N J 2001 Phys. Rev. 63 052311
[7] Dur W Vidal G Cirac J I 2000 Phys. Rev. 62 062314
[8] Lamont M. R. E. Okawachi Y. Gaeta A. L. 2013 Opt. Lett. 38 3478
[9] Bourennane M Karlsson A Björk G 2001 Phys. Rev. 64 012306
[10] Mair A Vaziri G W A Zeilinger A 2001 Nature 412 313
[11] Kawase D Miyamoto Y Takeda M Sasaki K Takeuchi S 2008 Phys. Rev. Lett. 101 050501
[12] Pors J B Oemrawsingh S S R Aiello A van Exter M P Eliel E R Hooft G W Woerdman J P 2008 Phys. Rev. Lett. 101 120502
[13] Malik M O’Sullivan M Rodenburg B Mirhosseini M Leach J Lavery M P J Padgett M J Boyd R W 2012 Opt. Express 20 13195
[14] Rodenburg B Mirhosseini M Malik M Magaña-Loaiza O S Yanakas M Maher L Steinhoff N K Tyler G A Boyd R. W. 2014 New J. Phys. 16 033020
[15] Gopaul C Andrews R 2007 New J. Phys. 9 94
[16] Sheng X Zhang Y Zhao F Zhang L Zhu Y 2012 Opt. Lett. 37 2607
[17] Smith B J Raymer M G 2006 Phys. Rev. 74 062104
[18] Pros B J Monken C H Elie E R Woerdman P 2011 Opt. Express 19 6671
[19] Roux F S 2011 Phys. Rev. 83 053822
[20] Brünner T Roux F S 2013 New J. Phys. 15 063005
[21] Cunha Pereira M V Filpi L A P Monken C H 2013 Phys. Rev. 88 053836
[22] Ibrahim A H Roux F S Mclaren M Thomas K Forbes A 2013 Phys. Rev. 88 012312
[23] Gonzalez Alonso J R Brun T A 2013 Phys. Rev. 88 022326
[24] Zou L Wang L Zhao S M Chen H W 2016 Chin. Phys. 25 114215
[25] Paterson C 2005 Phys. Rev. Lett. 94 153901
[26] Jha A K Tyler G A Boyd R W 2010 Phys. Rev. 81 053832
[27] Yan X Zhang P F Zhang J H Qiao C H Fan C Y 2016 J. Opt. Soc. Am. 33 1831
[28] Ibrahim A H Roux F S Konrad T 2014 Phys. Rev. 90 052115
[29] Roux F S 2014 J. Phys. A: Math. Theor. 47 195302
[30] Leonhard N D Shatokhin V N Buchleitner A 2015 Phys. Rev. 91 012345
[31] Zhao S M Leach J Gong L Y Ding J Zheng B Y 2012 Opt. Express 20 452
[32] Coffman V Kundu J Wootters W K 2000 Phys. Rev. 61 052306
[33] Stribling B E Welsh B M Roggemann M C 1995 Proc. SPIE 2471 181