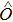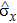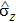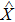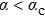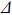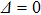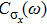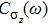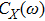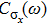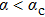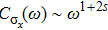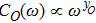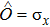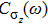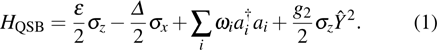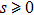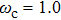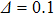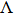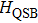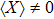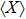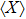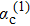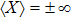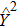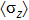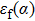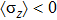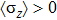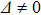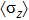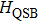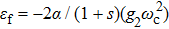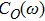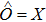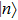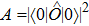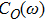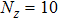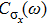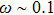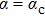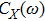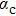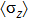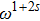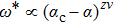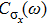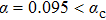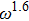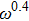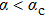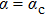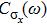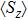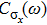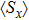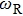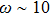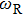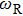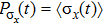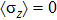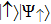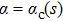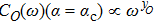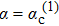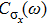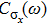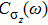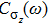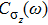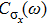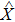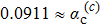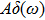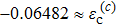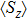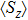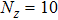1. IntroductionThe spin-boson model (SBM) is a frequently used paradigm to study the influence of the environmental noise on the quantum evolution of a two-level system.[1,2] The environment-induced dissipation and dephasing are the key issues in many fields of physics, ranging from biology to the endeavor of building a quantum computer.[3] Sufficiently strong coupling to the boson bath also induces localized–delocalized quantum phase transitions (QPTs) in the two-level system for the Ohmic and sub-Ohmic baths.[1,2,4–8] The non-trivial universality class of these QPTs has received a great deal of attention in recent years[9–17] and the experimental detection of such QPTs has been proposed.[18–22]
In the conventional spin-boson model, a spin which describes the two-level quantum system is coupled linearly to the displacement operator of a group of harmonic oscillators which are used to describe the environmental noise. Recently, in the experiments of the superconducting quantum bit (qubit) system, the linear qubit-environment coupling can be tuned to zero to suppress the decoherence. Significant enhancement of the coherence time was observed in experiments at such an optimal working point.[23–27] Motivated by these experimental progresses, a greatdeal of attention is paid to the spin-boson model with a quadratic coupling, which is the leading term at the optimal working point. Theoretical studies of the quadratic-coupling spin-boson model (QSBM) have been carried out, mainly focusing on the dissipation and decohrence of the qubit.[28–31] QSBM is also studied in other contexts such as the quantum dot-based qubit systems[32,33] and the quantum Brownian motion of a heavy particle.[34]
In a recent work,[35] we studied the zero temperature properties of the sub-Ohmic QSBM using the numerical renormalzation group (NRG) method.[36,37] We found that the bosonic environment is unstable towards local distortion under sufficiently strong quadratic spin-boson coupling, resulting in a novel impurity-induced environmental QPT in this model. We produced a ground state phases diagram on the ε (bias)–α (coupling strength) plane which contains both the continuous and the first-order QPTs. On this phase diagram,
 changes sign at the so-called spin-flip line which is a first-order transition line at
changes sign at the so-called spin-flip line which is a first-order transition line at
 but becomes a continuous crossover line at
but becomes a continuous crossover line at
 (
(
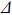 is the tunnelling strength of the quantum two-level systems, see below.). The critical exponents of the QPT are obtained exactly from the exact solution at
is the tunnelling strength of the quantum two-level systems, see below.). The critical exponents of the QPT are obtained exactly from the exact solution at
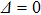 . The equilibrium dynamical correlation functions of the z component of spin
. The equilibrium dynamical correlation functions of the z component of spin
 , and that of the bath displacement operator
, and that of the bath displacement operator
 are analyzed near the QPT. These results disclosed the strong impurity-bath mutual influence due to the non-linearity of the coupling.
are analyzed near the QPT. These results disclosed the strong impurity-bath mutual influence due to the non-linearity of the coupling.
In this paper, using NRG, we explore the evolution of the equilibrium dynamical correlation functions
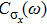 as the parameters ε and α are tuned throughout the phase diagram. To make comparisons, we also summarize the results for
as the parameters ε and α are tuned throughout the phase diagram. To make comparisons, we also summarize the results for
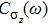 and
and
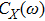 which have been obtained in Ref. [35]. These correlation functions reflect important properties of the model.
which have been obtained in Ref. [35]. These correlation functions reflect important properties of the model.
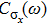 and
and
 contains information about the dissipation and decoherence of the spin, respectively.
contains information about the dissipation and decoherence of the spin, respectively.
 characterizes the bath which is severely influenced by the presence of the impurity in the case of the non-linear coupling. We find that in the weak-coupling regime
characterizes the bath which is severely influenced by the presence of the impurity in the case of the non-linear coupling. We find that in the weak-coupling regime
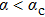 , all the three correlation functions have the power law form in the small frequency limit.
, all the three correlation functions have the power law form in the small frequency limit.
 reflects the power law spectral function of the bath that we used
reflects the power law spectral function of the bath that we used
 .
.
 is similar to
is similar to
 ,[35] with the form
,[35] with the form
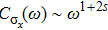 . At the critical point
. At the critical point
 ,
,
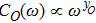 in the small frequency limit (
in the small frequency limit (
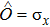 , σz, and X). We find that
, σz, and X). We find that
 and
and
 . In the higher frequency regime close to the Rabi frequency ωR, both
. In the higher frequency regime close to the Rabi frequency ωR, both
 and
and
 have a prominent peak even at the strongest coupling
have a prominent peak even at the strongest coupling
 before the environment gets unstable. Close to the spin-flip line, a significant broadening of the Rabi peak is observed in
before the environment gets unstable. Close to the spin-flip line, a significant broadening of the Rabi peak is observed in
 but not in
but not in
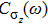 , showing an enhanced decoherence at the spin-flip line of the optimal working point.
, showing an enhanced decoherence at the spin-flip line of the optimal working point.
This paper is organized as the following. In Section 2 we introduce QSBM and the formalism we used to calculate the equilibrium correlation function with the bosonic NRG method. Section 3 presents results from our NRG study. A conclusion is given in Section 4.
2. Model and methodThe Hamiltonian of the quadratic coupling spin-boson model reads
The two-level system is described by a spin-1/2 operator with the bias
ε and tunnelling strength

. It is coupled to the bosonic bath with mode energies

via the local boson displacement operator

.
g2 is the second-order coefficient in the expansion of a general coupling form

. At the optimal working point of the superconducting qubit circuit,

and the remaining leading order coupling is
g2. The effect of the bath on the spin is encoded into the bath spectral function
Although the QPT exists also for the single mode quadratic coupling Hamiltonian which is relevant to the qubit-resonator system,
[38,39] in this paper we mainly focus on the continuous bath with a power law spectrum in the small
ω limit and a hard-cutoff at

,
Here
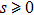
is the exponent of the bath spectrum and
α controls the strength of the spin-boson coupling. We set
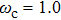
as the unit of energy. The quadratic coefficient
g2 can be absorbed into
λiʼs and for convenience we set it as unity. In this paper, we fix
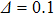
to study the dependence of the equilibrium dynamics on
ε and
α. We confine our study to the sub-Ohmic bath with

. For definiteness, we use a generic value
s = 0.3 in most parts of this paper and discuss the extension of our conclusion to the full sub-Ohmic regime in the end.
We will use the bosonic NRG method to study this model. NRG is regarded as one of the most powerful methods for studying quantum impurity models because it is non-perturbative and reliable in the full parameter space.[36,37] In general, the errors in the NRG calculation come from two sources. One is the approximation of using one bath mode to represent each energy shell, which is controlled by the logarithmic discretization parameter
 . The other is the truncation of the energy spectrum after each diagonalization to overcome the exponential increase of the Hilbert space, which is controlled by the number of kept states Ms. For the bosonic NRG, an additional source of error is the truncation of infinite dimensional Hilbert space of each boson mode into Nb states on the occupation basis. Exact results can be obtained only in the limit Λ = 1,
. The other is the truncation of the energy spectrum after each diagonalization to overcome the exponential increase of the Hilbert space, which is controlled by the number of kept states Ms. For the bosonic NRG, an additional source of error is the truncation of infinite dimensional Hilbert space of each boson mode into Nb states on the occupation basis. Exact results can be obtained only in the limit Λ = 1,
 , and
, and
 . Details of the application of NRG to
. Details of the application of NRG to
 can be found in Ref. [35].
can be found in Ref. [35].
In Fig. 1, we reprint the NRG phase diagram for s = 0.3 from Ref. [35]. It is obtained using the NRG parameters Λ = 4.0,
 , and
, and
 . Though the phase boundaries depend quantitatively on the NRG parameters, the qualitative topology of the phase diagram is unchanged when we extrapolate
. Though the phase boundaries depend quantitatively on the NRG parameters, the qualitative topology of the phase diagram is unchanged when we extrapolate
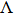 , Ms, and Nb to the exact limit.[35] In Fig. 1, the ground state of
, Ms, and Nb to the exact limit.[35] In Fig. 1, the ground state of
 in the ε–α plane is characterized by two physical quantities,
in the ε–α plane is characterized by two physical quantities,
 and
and
 . Here
. Here
 is the normalized local boson displacement operator. On the left-hand side of the phase diagram (smaller α), the symmetry of
is the normalized local boson displacement operator. On the left-hand side of the phase diagram (smaller α), the symmetry of
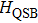 allows
allows
 to fluctuate symmetrically around zero while keeping the spin polarized, giving
to fluctuate symmetrically around zero while keeping the spin polarized, giving
 . On the right-hand side of the phase diagram (larger α), the coupling is sufficiently strong so that the harmonic oscillators in the environment get softened and inversion of the harmonic potentials of the low energy modes occurs, leading to the breaking of the symmetry of
. On the right-hand side of the phase diagram (larger α), the coupling is sufficiently strong so that the harmonic oscillators in the environment get softened and inversion of the harmonic potentials of the low energy modes occurs, leading to the breaking of the symmetry of
 and
and
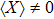 . Therefore,
. Therefore,
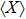 is the order parameter of this environmental QPT. The QPT between the two phases is continuous (empty circles with eye-guiding line) for larger ε and is of first order (empty squares with eye-guiding line) for smaller ε. At the first-order QPT,
is the order parameter of this environmental QPT. The QPT between the two phases is continuous (empty circles with eye-guiding line) for larger ε and is of first order (empty squares with eye-guiding line) for smaller ε. At the first-order QPT,
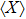 jumps abruptly from zero to a finite value. We denote the critical coupling strength as
jumps abruptly from zero to a finite value. We denote the critical coupling strength as
 for the former and
for the former and
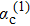 for the latter. These two kinds of QPT lines meet at the jointing point (
for the latter. These two kinds of QPT lines meet at the jointing point (
 ,
,
 ) (solid circle in Fig. 1) where the finite jump in
) (solid circle in Fig. 1) where the finite jump in
 at
at
 shrinks to zero. For the Hamiltonian Eq. (1),
shrinks to zero. For the Hamiltonian Eq. (1),
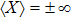 in the environment-unstable phase. If the higher order anharmonic terms of the bosons beyond Eq. (1) are considered,
in the environment-unstable phase. If the higher order anharmonic terms of the bosons beyond Eq. (1) are considered,
 will be confined to a finite value in the boson-unstable phase. The boson-unstable phase then describes the physical situation where the environmental degrees of freedom have a local distortion around the impurity.
will be confined to a finite value in the boson-unstable phase. The boson-unstable phase then describes the physical situation where the environmental degrees of freedom have a local distortion around the impurity.
Since the instability of bosons in the strong coupling regime only occurs when the pre-factor of
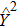 is negative in the coupling term of
is negative in the coupling term of
 , the above QPTs occur either with
, the above QPTs occur either with
 on both sides of the transition (upper part of Fig. 1), or with
on both sides of the transition (upper part of Fig. 1), or with
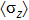 changing from positive to negative (lower part of Fig. 1). In the boson-stable regime, there is a spin flip line
changing from positive to negative (lower part of Fig. 1). In the boson-stable regime, there is a spin flip line
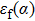 (up triangles with eye-guiding line) which separates
(up triangles with eye-guiding line) which separates
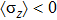 from
from
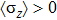 . For
. For
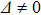 ,
,
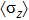 continuously crosses zero at this line.
continuously crosses zero at this line.
At Δ = 0,
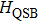 is exactly soluble because the two subspaces with
is exactly soluble because the two subspaces with
 are decoupled.[35] The phase diagram is qualitatively the same as the one for
are decoupled.[35] The phase diagram is qualitatively the same as the one for
 shown in Fig. 1. The exact critical coupling strength is obtained as
shown in Fig. 1. The exact critical coupling strength is obtained as
 . The spin flip line is the exact level crossing line between the two subspaces with
. The spin flip line is the exact level crossing line between the two subspaces with
 . To the leading order of α, the spin flip line is given by
. To the leading order of α, the spin flip line is given by
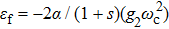 . For a finite
. For a finite
 , the NRG study showed that the spin flip line becomes a smooth crossover line without singularity.
, the NRG study showed that the spin flip line becomes a smooth crossover line without singularity.
Below, in order to further explore the dissipation and decoherence of the quantum two-level system subjected to the influence of a bath with quadratic coupling, we study the dynamical correlation function at T = 0 using NRG. The dynamical correlation function of an operator
 is defined as
is defined as
where

is the anti-commutator of

and

. What we calculate directly is its Fourier transformation
In this paper, we study
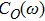
at zero temperature for the following operators

,

, and
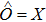
. For a non-degenerate ground state, the Lehmann representation of

at
T = 0 is written as
Here
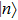
and
En are the
n-th eigen-state and energy of the Hamiltonian, respectively. In general,

, where
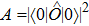
and

is the ground state.

is an even function of
ω and it fulfils the sum rule
 | |
Within NRG,
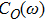 can be calculated using the patching method.[40] In this method, the poles and weights obtained from the diagonalization of each Wilson chain Hamiltonian HN are collected and patched together, to form a full spectrum ranging from high energy to the lowest energy reachable by NRG. The obtained δ-peaks are then broadened using the log-Gaussian function with a broadening parameter B. In the patching method, the sum rule of
can be calculated using the patching method.[40] In this method, the poles and weights obtained from the diagonalization of each Wilson chain Hamiltonian HN are collected and patched together, to form a full spectrum ranging from high energy to the lowest energy reachable by NRG. The obtained δ-peaks are then broadened using the log-Gaussian function with a broadening parameter B. In the patching method, the sum rule of
 is fulfilled approximately, with a relative error at the level of a few percent. The more sophisticated full density matrix method[41,42] can conserve the sum rule exactly but the positivity of
is fulfilled approximately, with a relative error at the level of a few percent. The more sophisticated full density matrix method[41,42] can conserve the sum rule exactly but the positivity of
 is not guaranteed. In general, the NRG method can give a rather accurate low frequency spectral function, but the high frequency part is less reliable due to the loss of energy resolution from logarithmic discretization and the over broadening of the log-Gaussian function. There are attempts to improve the high frequency resolution within the NRG method[43–50] with various levels of success. In this paper, we calculate the above-stated correlation functions using the patching method with a broadening parameter B = 1.0. To improve the resolution of certain high frequency features, we use the z-average method[43,44] with the number of z values
is not guaranteed. In general, the NRG method can give a rather accurate low frequency spectral function, but the high frequency part is less reliable due to the loss of energy resolution from logarithmic discretization and the over broadening of the log-Gaussian function. There are attempts to improve the high frequency resolution within the NRG method[43–50] with various levels of success. In this paper, we calculate the above-stated correlation functions using the patching method with a broadening parameter B = 1.0. To improve the resolution of certain high frequency features, we use the z-average method[43,44] with the number of z values
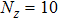 and a reduced broadening parameter B = 0.3.
and a reduced broadening parameter B = 0.3.
3. ResultsIn order to explore the evolution of the dynamical correlation functions
 (for
(for
 , σz, and X) with ε and
, σz, and X) with ε and
 , we scan the parameters along two representative paths on the ε–α plane. First, we fix ε = 0.0 and increase α (stars along the horizontal dashed line in Fig. 1). Second, we fix α =0.095 and increase ε (stars along the vertical dashed line in Fig. 1). Both paths are confined in the boson-stable phase. The obtained
, we scan the parameters along two representative paths on the ε–α plane. First, we fix ε = 0.0 and increase α (stars along the horizontal dashed line in Fig. 1). Second, we fix α =0.095 and increase ε (stars along the vertical dashed line in Fig. 1). Both paths are confined in the boson-stable phase. The obtained
 ʼs are plotted in Fig. 2 and Fig. 3, respectively, for making systematic comparisons.
ʼs are plotted in Fig. 2 and Fig. 3, respectively, for making systematic comparisons.
In Figs. 2(a)–2(c), we show
 on the logarithmic scale calculated at ε = 0 and for a series of α values.
on the logarithmic scale calculated at ε = 0 and for a series of α values.
 , σz, and X for Figs. 2(a), 2(b), and 2(c), respectively. In each figure, the curves from bottom to top correspond to increasing α values. For such a series of parameters,
, σz, and X for Figs. 2(a), 2(b), and 2(c), respectively. In each figure, the curves from bottom to top correspond to increasing α values. For such a series of parameters,
 and
and
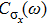 are quantitatively similar, both composed of the low frequency power law behavior and the high frequency peak around
are quantitatively similar, both composed of the low frequency power law behavior and the high frequency peak around
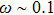 . The broad peak is to much extent due to the log-Gaussian broadening of an actually much narrower Rabi coherent peak. The fitted values of the low frequency exponents are numerically close for
. The broad peak is to much extent due to the log-Gaussian broadening of an actually much narrower Rabi coherent peak. The fitted values of the low frequency exponents are numerically close for
 and
and
 , being approximately 1.6 for
, being approximately 1.6 for
 and 0.4 for
and 0.4 for
 .
.
 has a similar behavior but lacks the coherent peak around the Rabi frequency. The corresponding exponents are close to 0.3 and −0.3, respectively. The calculation for other s values shows that the exponents of
has a similar behavior but lacks the coherent peak around the Rabi frequency. The corresponding exponents are close to 0.3 and −0.3, respectively. The calculation for other s values shows that the exponents of
 and
and
 agree with the expressions 1+2s for
agree with the expressions 1+2s for
 and
and
 for
for
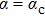 . The corresponding exponents of
. The corresponding exponents of
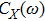 are s and −s, respectively, as being obtained exactly in Ref. [35].
are s and −s, respectively, as being obtained exactly in Ref. [35].
We note that as α approaches
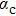 from below, the static averages
from below, the static averages
 and
and
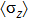 change very slowly and they have negligible influence on the evolution of correlation functions. In this process, the crossover scale
change very slowly and they have negligible influence on the evolution of correlation functions. In this process, the crossover scale
 separating the high frequency
separating the high frequency
 to the low frequency
to the low frequency
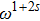 behavior decreases to zero as
behavior decreases to zero as
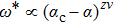 , with z = 1 being the dynamical exponent and ν the correlation length exponent (Ref. [35]). In contrast, the high frequency peaks of both
, with z = 1 being the dynamical exponent and ν the correlation length exponent (Ref. [35]). In contrast, the high frequency peaks of both
 and
and
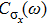 do not change much. This stability of the peak position and line shape of the coherent peak implies a robust coherent short-time quantum evolution and the weak dissipation and docoherence effects near the quantum critical point.
do not change much. This stability of the peak position and line shape of the coherent peak implies a robust coherent short-time quantum evolution and the weak dissipation and docoherence effects near the quantum critical point.
In Fig. 3, to investigate the evolution of the correlation functions in a different path, we fix
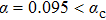 and increase ε up to the QPT line. Compared to the evolution shown in Fig. 2, some interesting features are observed here. First, the low frequency behavior is similar to that of Fig. 2, i.e.,
and increase ε up to the QPT line. Compared to the evolution shown in Fig. 2, some interesting features are observed here. First, the low frequency behavior is similar to that of Fig. 2, i.e.,
 and
and
 have power law form
have power law form
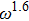 for
for
 and the critical behavior
and the critical behavior
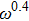 at
at
 . With increasing ε, the low frequency value of
. With increasing ε, the low frequency value of
 increases monotonically.
increases monotonically.
 for
for
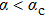 and
and
 at
at
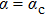 , with the crossover bahavior similar to that of Fig. 2(c). The high frequency features are quite different from those of Fig. 2. Here, the height and line shape of the high frequency peaks of
, with the crossover bahavior similar to that of Fig. 2(c). The high frequency features are quite different from those of Fig. 2. Here, the height and line shape of the high frequency peaks of
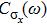 and
and
 change significantly with increasing ε, in contrast to those of Fig. 2. Note that both Fig. 3(a) and Fig. 3(b) have a δ-peak at zero frequency, whose weights change un-monotonically with ε, as shown in Fig. 4. As ε increases, the redistribution of weights between the zero-frequency δ-peak and the finite frequency regime do account for part of the evolution shown in Fig. 3(b). As ε increases from −0.4 to −0.16,
change significantly with increasing ε, in contrast to those of Fig. 2. Note that both Fig. 3(a) and Fig. 3(b) have a δ-peak at zero frequency, whose weights change un-monotonically with ε, as shown in Fig. 4. As ε increases, the redistribution of weights between the zero-frequency δ-peak and the finite frequency regime do account for part of the evolution shown in Fig. 3(b). As ε increases from −0.4 to −0.16,
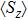 decreases from 0.5 to almost zero (see inset of Fig. 4). This leads to a decrease of the zero frequency weights and explains the uniform increase of
decreases from 0.5 to almost zero (see inset of Fig. 4). This leads to a decrease of the zero frequency weights and explains the uniform increase of
 in this ε regime, as shown in Fig. 3(b). However, the line shape change of the high frequency peak in
in this ε regime, as shown in Fig. 3(b). However, the line shape change of the high frequency peak in
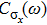 in Fig. 3(a) cannot be simply attributed to it. This shows that the short-time decoherence in QSBM has some anomalous dependence on ε for a fixed coupling strength α.
in Fig. 3(a) cannot be simply attributed to it. This shows that the short-time decoherence in QSBM has some anomalous dependence on ε for a fixed coupling strength α.
To further investigate the evolution of the high frequency peak of
 with ε, which is relevant to the dephasing time in the qubit experiment at the optimal working point, we use the z-average method to improve the frequency resolution. In Fig. 4, we show the high frequency peak of
with ε, which is relevant to the dephasing time in the qubit experiment at the optimal working point, we use the z-average method to improve the frequency resolution. In Fig. 4, we show the high frequency peak of
 at the same parameters as in Fig. 3, for various ε values. Each curve is the averaged result over
at the same parameters as in Fig. 3, for various ε values. Each curve is the averaged result over
 uniformly distributed z values with a smaller broadening parameter B = 0.3. Though the z-average method cannot remove all the errors of logarithmic discretization, it is argued to be useful for improving the resolution of high frequency features and remove the oscillations induced by a smaller broadening parameter.[43,44] In the inset of Fig. 4, the averages
uniformly distributed z values with a smaller broadening parameter B = 0.3. Though the z-average method cannot remove all the errors of logarithmic discretization, it is argued to be useful for improving the resolution of high frequency features and remove the oscillations induced by a smaller broadening parameter.[43,44] In the inset of Fig. 4, the averages
 and
and
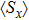 are shown as functions of ε in the regime
are shown as functions of ε in the regime
 . The vertical dashed line marks out the spin flip point
. The vertical dashed line marks out the spin flip point
 . The horizontal dashed line marks out
. The horizontal dashed line marks out
 . Besides the shifts of peak position with ε, significant change of the line shape of the high frequency peak in
. Besides the shifts of peak position with ε, significant change of the line shape of the high frequency peak in
 occurs close to the spin flip point
occurs close to the spin flip point
 . Close to this value of ε, the high frequency peak is significantly broadened and the line shape is no longer a round peak. Away from this value of ε, a relatively sharp peak appears at the effective Rabi frequencies
. Close to this value of ε, the high frequency peak is significantly broadened and the line shape is no longer a round peak. Away from this value of ε, a relatively sharp peak appears at the effective Rabi frequencies
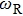 on top of a broad background spectrum extending to
on top of a broad background spectrum extending to
 .
.
The peak position is at the effective Rabi frequency
 . It can be estimated by assuming a free spin Hamiltonian
. It can be estimated by assuming a free spin Hamiltonian
 . The effective bias
. The effective bias
 contains both the original ε and the contribution from the static mean field of the quadratic coupling
contains both the original ε and the contribution from the static mean field of the quadratic coupling
 in
in
 .
.
 is the renormalized tunnelling strength. We use the NRG data of
is the renormalized tunnelling strength. We use the NRG data of
 to solve for
to solve for
 and then
and then
 . The obtained
. The obtained
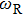 ʼs (vertical dashes in Fig. 4) agree well with the peak position in
ʼs (vertical dashes in Fig. 4) agree well with the peak position in
 , except for ε = −0.16 close to the spin flip point. For ε = −0.16, the fitted
, except for ε = −0.16 close to the spin flip point. For ε = −0.16, the fitted
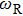 is located at the lower edge of a broad feature (which cannot be called a peak). It has been confirmed that at least for the weak coupling regime, the evolution of dynamical correlation function C(t) is similar to P(t), the average of the corresponding operator in the non-equilibrium situation.[51] A sharp high frequency peak in
is located at the lower edge of a broad feature (which cannot be called a peak). It has been confirmed that at least for the weak coupling regime, the evolution of dynamical correlation function C(t) is similar to P(t), the average of the corresponding operator in the non-equilibrium situation.[51] A sharp high frequency peak in
 corresponds to coherent oscillations in
corresponds to coherent oscillations in
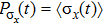 and it implies a weak dephasing effect. The vanishing of the peak close to the spin flip point at ε = −0.16 thus corresponds to incoherent evolution with stronger dephasing effect.
and it implies a weak dephasing effect. The vanishing of the peak close to the spin flip point at ε = −0.16 thus corresponds to incoherent evolution with stronger dephasing effect.
In NRG, the δ-peaks in the spectral function are obtained from iterative diagonalization of the logarithmically-discretized energy shells. They are then broadened by log-Gaussian functions. It is therefore difficult to tell the exact line shape of a high frequency peak from the raw NRG data, despite great efforts paid to improve on this problem.[43–50] Here, however, the qualitative tendency gives a robust conclusion that close to the spin flip line, the decoherence peak in
 is broadened and the line shape changed qualitatively. This result, when translated into the non-equilibrium quantity, suggests that the dephasing time of the qubit may decrease significantly close to the spin flip line, being unfavorable to the realization of a long-lived qubit. Physically, from the point of view of the weak
is broadened and the line shape changed qualitatively. This result, when translated into the non-equilibrium quantity, suggests that the dephasing time of the qubit may decrease significantly close to the spin flip line, being unfavorable to the realization of a long-lived qubit. Physically, from the point of view of the weak
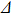 limit, the spin flip line at which
limit, the spin flip line at which
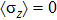 can be approximately regarded as the degeneracy point of two (approximate) subspaces
can be approximately regarded as the degeneracy point of two (approximate) subspaces
 . The real quantum state is thus a superposition of
. The real quantum state is thus a superposition of
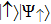 and
and
 (two eigen-states of σz) with equal weights. The energy fluctuations of these states due to coupling to bosons have a stronger effect in destroying the phase coherence in the superposition, leading to an enhanced dephasing at the spin flip point.
(two eigen-states of σz) with equal weights. The energy fluctuations of these states due to coupling to bosons have a stronger effect in destroying the phase coherence in the superposition, leading to an enhanced dephasing at the spin flip point.
The above results are obtained for the sub-Ohmic bath with s = 0.3. We have carried out systematic calculations for other sub-Ohmic s values as well. In Fig. 5, we show the dynamical correlation functions for a series of s values at
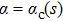 , in order to find out the critical exponents yO defined as
, in order to find out the critical exponents yO defined as
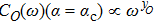 . The fitted exponents from NRG data supports that
. The fitted exponents from NRG data supports that
 . Our results here confirm that
. Our results here confirm that
 and
and
 found in Ref. [35]. For
found in Ref. [35]. For
 , the power law in the low frequency limit is obtained as
, the power law in the low frequency limit is obtained as
 ,
,
 , and
, and
 (data not shown). Close to the spin flip line, the significant broadening of the high frequency peak in
(data not shown). Close to the spin flip line, the significant broadening of the high frequency peak in
 and the change of the line shape are found to be universal for all sub-Ohmic regimes.
and the change of the line shape are found to be universal for all sub-Ohmic regimes.
Note that in Fig. 5, the critical power law behavior for s = 0.7 only appears in the high frequency regime
 and does not extend to arbitrarily small ω. This is because for s = 0.7, Δ = 0.1, and ε = 0.1, a first-order QPT occurs at
and does not extend to arbitrarily small ω. This is because for s = 0.7, Δ = 0.1, and ε = 0.1, a first-order QPT occurs at
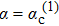 . It was found[35] that as s increases, the impurity-induced environmental QPT tends to become first order. Close to this QPT
. It was found[35] that as s increases, the impurity-induced environmental QPT tends to become first order. Close to this QPT
 , one can still observe the quantum criticality in the high frequency regime. This fact is interesting in that it shows an example of observing the quantum critical properties close to a weak first-order QPT which is much more prevailing than a continuous QPT in the experiments. Details of this issue will be studied elsewhere.
, one can still observe the quantum criticality in the high frequency regime. This fact is interesting in that it shows an example of observing the quantum critical properties close to a weak first-order QPT which is much more prevailing than a continuous QPT in the experiments. Details of this issue will be studied elsewhere.