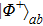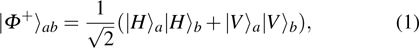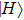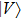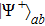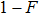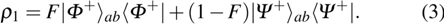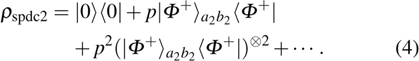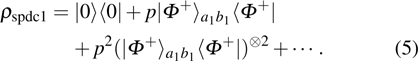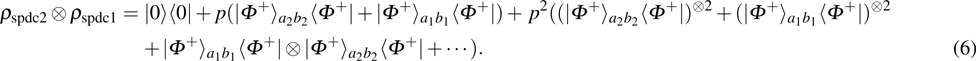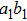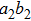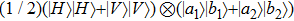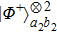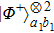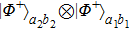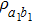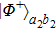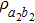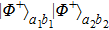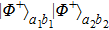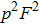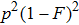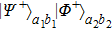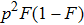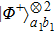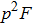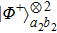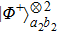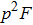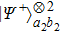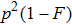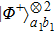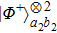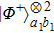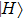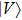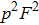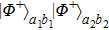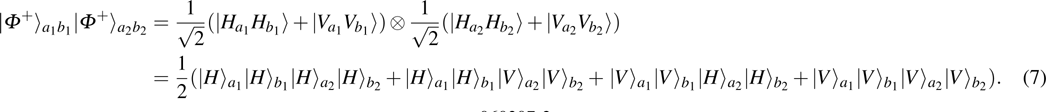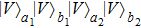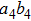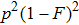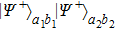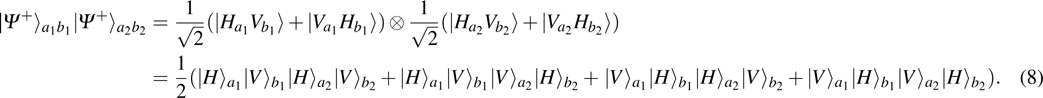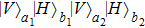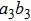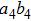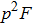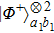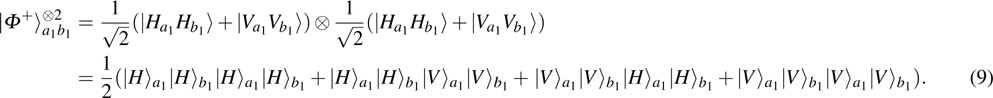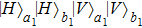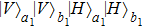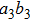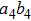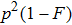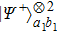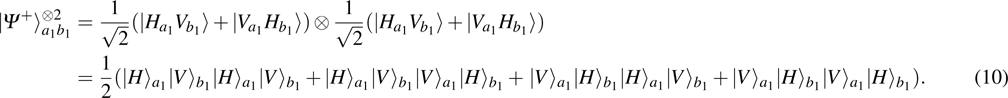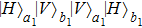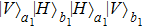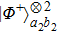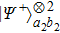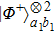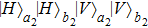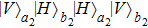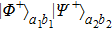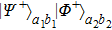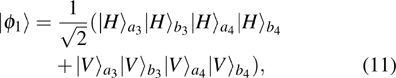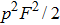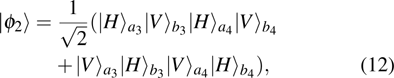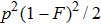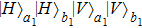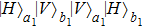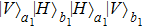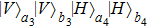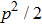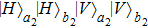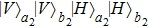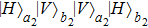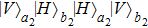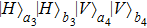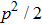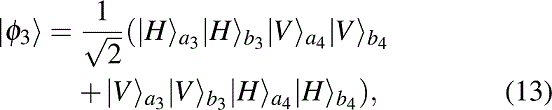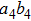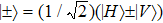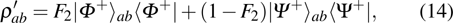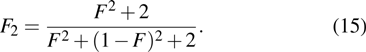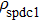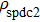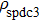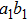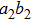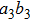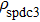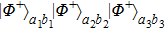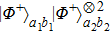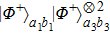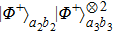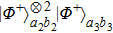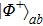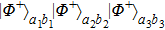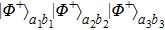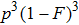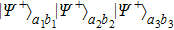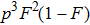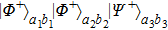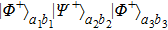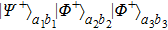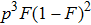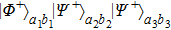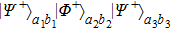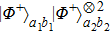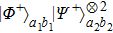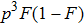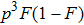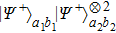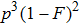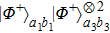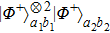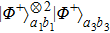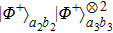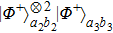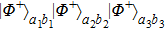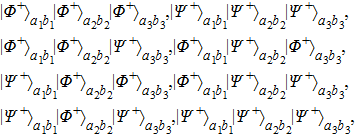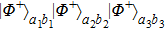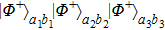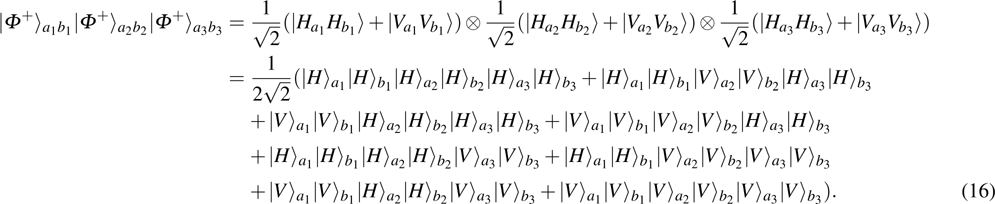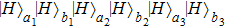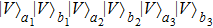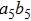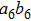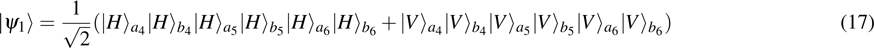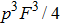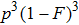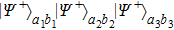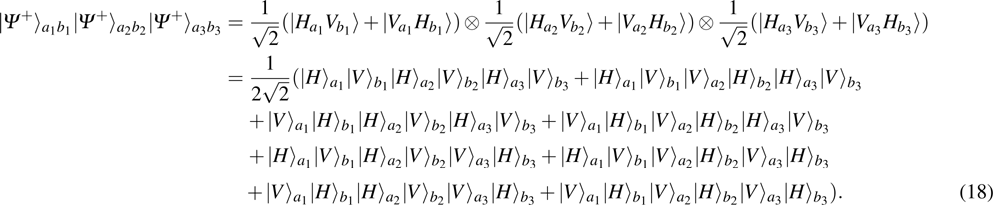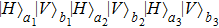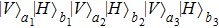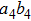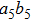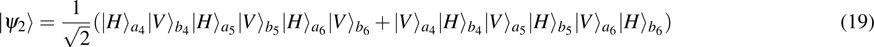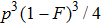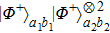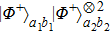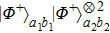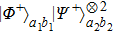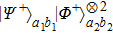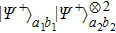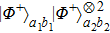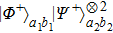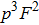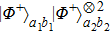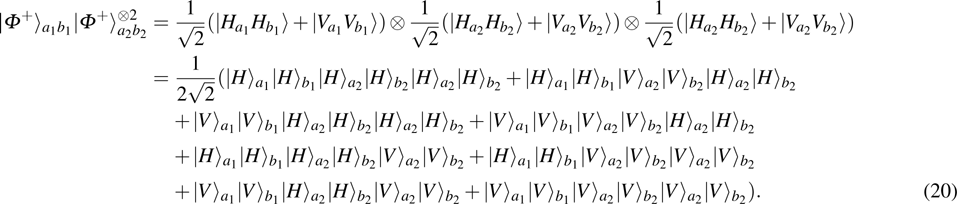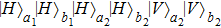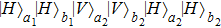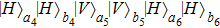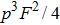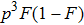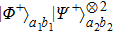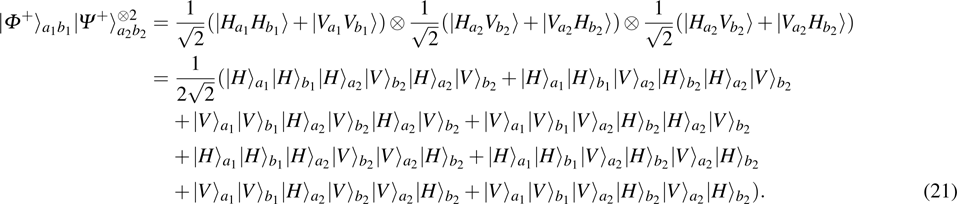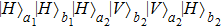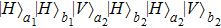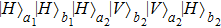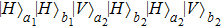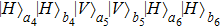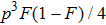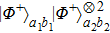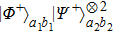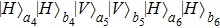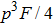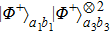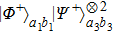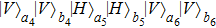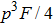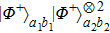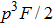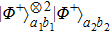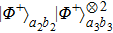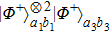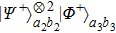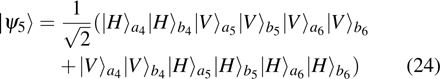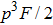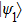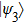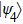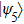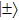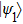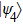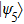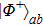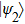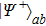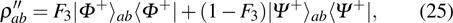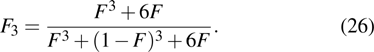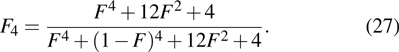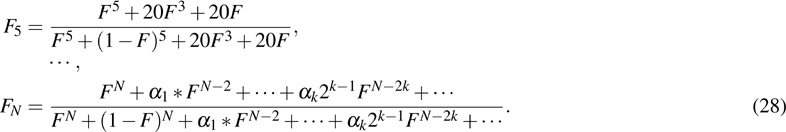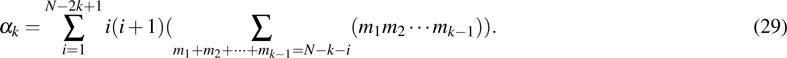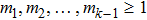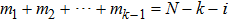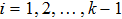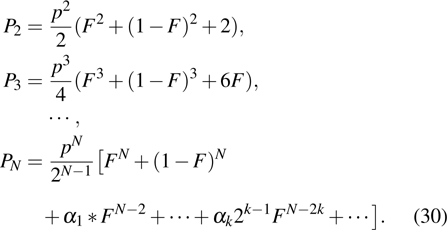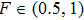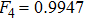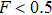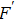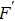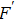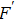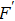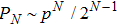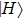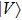Multi-copy entanglement purification with practical spontaneous parametric down conversion sources
1. IntroductionThe absolute security of quantum communication makes it have great value in future communication technologies. Many important protocols have been proposed, such as quantum teleportation,[1] quantum secure direct communication (QSDC),[2–5] quantum secret sharing (QSS),[6] quantum key distribution (QKD),[7–9] and some other interesting and important quantum communication and quantum information processing protocols.[10–18] In order to realize the long-distance quantum communication, high quality entanglement is the indispensable resource. However, entanglement can only be prepared locally and then be distributed in the free space or in a fiber. In a practical transmission, the distributed photons will inevitably suffer from the noise in environment. If the entangled quantum system degrades seriously, the quantum communication tasks cannot be well achieved. Moreover, the quantum communication will become insecure.
Entanglement purification is an important quantum technique to obtain the high quality entanglement from the low quality entanglement.[19] In 1996, Bennett et al. firstly proposed the concept of entanglement purification which attracted much attention.[19] Generally, existing entanglement purification protocols (EPPs) can be divided into three groups. The first group is to use one copy of degraded mixed state.[20–27] They are the deterministic EPPs which exploit the hyperentanglement or robust entanglement encoded in other degree of freedom. The second group which contains the most EPPs is to use two copies of degraded mixed states.[19,28–44] The third group is to use the multi-copy degraded mixed states.[45–50] In the third group, they usually exploit the controlled-not (CNOT) gates and controlled-controlled-not (CCNOT) gates to complete the purification. However, CNOT and CCNOT are not feasible in current experimental condition, which makes this kind of protocols be far away from current application. In 2015, Cai et al. described a fast multi-copy EPP.[50] Their protocol can obtain a high fidelity in one purification step and it does not require the sophisticated CNOT gate or CCNOT gate. The protocol only exploits the feasible polarization beam splitters (PBSs) and single-photon detectors. Similar to Ref. [29], the protocol in Ref. [50] still needs the ideal entanglement source. It is known that the ideal entanglement source is not available. Such obstacle will make this protocol still be far away from practical application.
In this paper, we will investigate the multi-copy EPP with practical spontaneous parametric down conversion (SPDC) sources. Interestingly, the SPDC source is not an obstacle in realization purification, but will benefit the protocol. The SPDC source makes us obtain a higher fidelity than the original protocol.[50] This EPP also requires the linear optics and is feasible in current experiment condition.
This paper is organized as follows. In Section 2, we will describe the basic model of this protocol and discuss the two-copy EPP with SPDC sources. In Section 3, we first discuss the three-copy EPP with SPDC sources and then extend this EPP to a more general case. In Section 4, we will provide a discussion and conclusion.
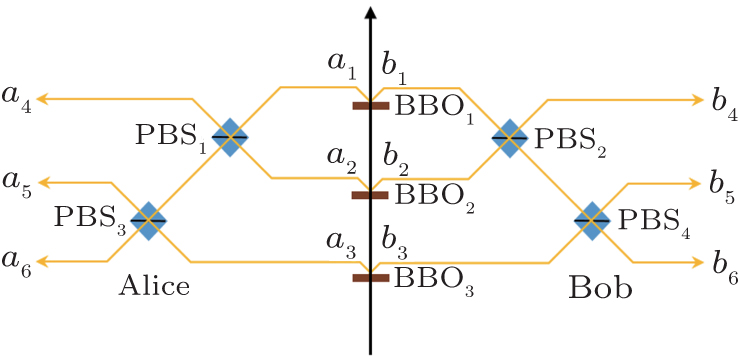
2. Two-copy EPP with SPDC sourcesThe basic model of the protocol is shown in Fig. 1, which is similar to Ref. [29]. Bob and Alice want to share the maximally entangled state
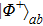 of the form
of the form
where
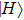
denotes the horizontally polarized photon and
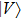
denotes the vertically polarized photon, respectively. The subscripts “
a” and “
b” are the spatial modes belonging to Alice and Bob, respectively. Because of the noise, the state

will become
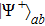
with the probability of
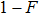
, which is called a bit-flip error. Here

can be written as
Then Alice and Bob will obtain a mixed state of the form
In order to realize the EPP, some EPPs should exploit the ideal entanglement source.
[28,29,50] Unfortunately, such ideal entanglement source is unavailable. Here we use the practical SPDC source to perform the EPP. As shown in Fig.
1, the pump passes through the first beta barium borate (BBO) crystal, named BBO
2, and produces correlated pair of photons in spatial modes
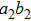
of the form
[20,32,51]Then the pump pass through the second BBO (BBO
1) and produces a second correlated pair of photons in spatial modes
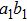
of the form
Therefore, state
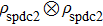
can be written as
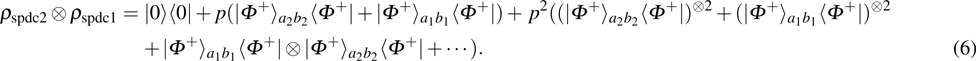 | |
From Eq. (6), the produced states in spatial modes
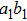 and
and
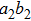 can be described as follows. With the probability of p, it is in the state
can be described as follows. With the probability of p, it is in the state
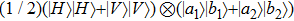 . It is essentially the hyperentanglement in both polarization and spatial mode degrees of freedom.[20,22,23,52] With the probability of p2, they are in the states
. It is essentially the hyperentanglement in both polarization and spatial mode degrees of freedom.[20,22,23,52] With the probability of p2, they are in the states
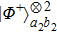 ,
,
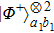 or
or
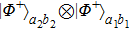 . If we consider the errors, the state
. If we consider the errors, the state
 will become
will become
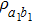 and
and
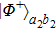 will become
will become
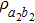 . In this way, the original states
. In this way, the original states
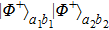 will become four possible cases. States are
will become four possible cases. States are
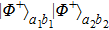 with a probability of
with a probability of
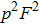 . States are
. States are
 with a probability of
with a probability of
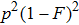 . States are
. States are
 and
and
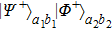 with an equal probability of
with an equal probability of
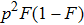 . Then for
. Then for
 , it becomes states
, it becomes states
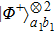 with a probability of
with a probability of
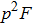 and states
and states
 with a probability of
with a probability of
 . Similarly, for
. Similarly, for
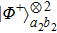 , it becomes states
, it becomes states
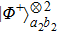 with a probability of
with a probability of
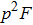 and states
and states
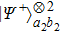 with a probability of
with a probability of
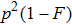 . Here we should point out that
. Here we should point out that
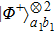 cannot become
cannot become
 , for the two pairs are emitted from the BBO simultaneously and they are always in the same position. The two pairs of photons always suffer from the same error. Therefore, they are always the same states.
, for the two pairs are emitted from the BBO simultaneously and they are always in the same position. The two pairs of photons always suffer from the same error. Therefore, they are always the same states.
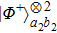 is analogy with
is analogy with
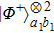 .
.
As shown in Fig. 1, PBSs can fully transmit the
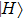 polarization photon and reflect the
polarization photon and reflect the
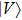 polarization photon, respectively. The key step of purification is to select the case that there is only one photon in each output mode which we call it four-mode case.
polarization photon, respectively. The key step of purification is to select the case that there is only one photon in each output mode which we call it four-mode case.
For example, with the probability of
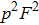 , states
, states
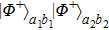 can be written as
can be written as
After passing through PBS
1 and PBS
2, only items

and
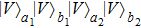
can make each of the output modes

and
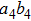
contain one photon. Similarly, with the probability of
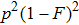
, states
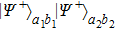
can be written as
After passing through PBS
1 and PBS
2, only items

and
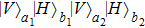
can make each of the output modes
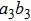
and
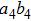
contain one photon. With the probability of
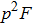
, states
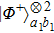
can be written as
After passing through PBS
1 and PBS
2, only items
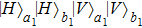
and
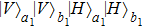
can make each of the output modes
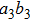
and
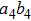
contain one photon. With the probability of
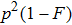
, states
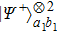
can be written as
After passing through PBS1 and PBS2, only items
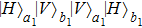 and
and
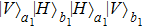 can make each of the output modes
can make each of the output modes
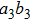 and
and
 contain one photon. States
contain one photon. States
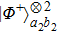 and
and
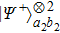 can also have the probability to cause the four-mode cases, similar to states
can also have the probability to cause the four-mode cases, similar to states
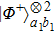 and
and
 , respectively, i.e., items
, respectively, i.e., items
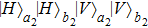 ,
,
 , and items
, and items
 ,
,
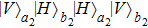 can satisfy four-mode case.
can satisfy four-mode case.
On the other hand, states
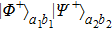 and
and
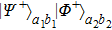 cannot satisfy the four-mode case. By selecting the four-mode case, one can obtain
cannot satisfy the four-mode case. By selecting the four-mode case, one can obtain
with the probability of
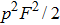
, and
with the probability of
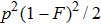
. For the rest of the states, which satisfy the four-mode case, the following states
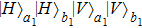
,

,
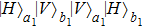
, and
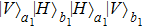
all become
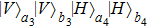
and the total probability is
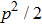
. Similarly
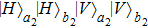
,
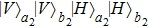
,
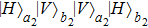
, and
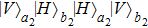
all become
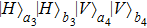
, and the probability is
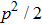
. Therefore, one can also obtain the state
with the probability of
p2. In order to get
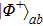
, one should measure the states above in spatial modes
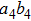
in the basis
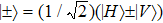
. Similar to Refs. [
29],[
30], and [
49], one can ultimately obtain a new mixed state
and the fidelity is
Here the subscription “2” means that the EPP with two copies of the mixed states.
3. Multi-copy EPP with SPDC sourcesIn this section, we will discuss the EPP with multi-copy mixed states. As shown in Fig. 2, the pump passes through three BBOs, and produces the entangled photon pairs
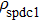 ,
,
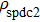 , and
, and
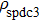 in spatial modes
in spatial modes
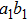 ,
,
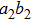 , and
, and
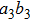 , respectively. Here
, respectively. Here
 ,
,
 , and
, and
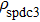 have the same form as shown in Eq. (4) and Eq. (5). In order to realize the EPP, we should select the six-mode case. That is each of the output modes a4, b4, a5, b5, a6, and b6 exactly registers one photon. Therefore, for the whole system
have the same form as shown in Eq. (4) and Eq. (5). In order to realize the EPP, we should select the six-mode case. That is each of the output modes a4, b4, a5, b5, a6, and b6 exactly registers one photon. Therefore, for the whole system
 , only items
, only items
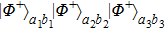 ,
,
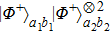 ,
,
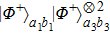 ,
,
 ,
,
 ,
,
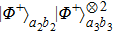 , and
, and
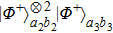 can satisfy the six-mode cases.
can satisfy the six-mode cases.
If the state
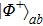 suffers from the noise, it will become a mixed state ρ1 as shown in Eq. (3). In this way, the original state
suffers from the noise, it will become a mixed state ρ1 as shown in Eq. (3). In this way, the original state
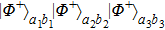 will become a mixture of the following states as given below.
will become a mixture of the following states as given below.
(i) With the probability of
 , they are in the states
, they are in the states
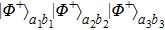 .
.
(ii) With the probability of
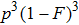 , they are in the states
, they are in the states
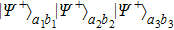 .
.
(iii) With the equal probability of
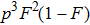 , they are in the states
, they are in the states
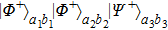 ,
,
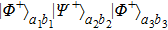 , and
, and
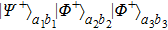 .
.
(iv) With the equal probability of
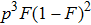 , they are in the states
, they are in the states
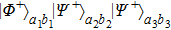 ,
,
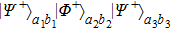 , and
, and
 , respectively.
, respectively.
For the states
 , it becomes states
, it becomes states
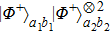 with the probability of
with the probability of
 , states
, states
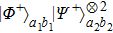 with the probability of
with the probability of
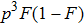 , states
, states
 with the probability of
with the probability of
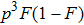 , and
, and
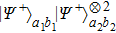 with the probability of
with the probability of
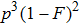 , respectively. The other states
, respectively. The other states
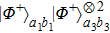 ,
,
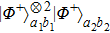 ,
,
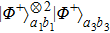 ,
,
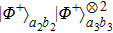 , and
, and
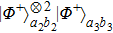 can also be described in the same principle.
can also be described in the same principle.
Similar to Section 2, the key step of this EPP is to select the case that there is only one photon in each output mode and we call it six-mode case. Firstly, we discuss the state
 .
.
Because of noise as described in the above discussion, the state
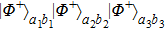 will become eight possible different states as
will become eight possible different states as
respectively. Interestingly, as shown in Fig.
2, after passing through the four PBSs, only states
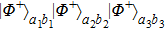
and

have the possibility to satisfy the six-mode case. For example, with the probability of
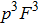
, states
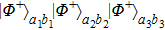
can be written as
After passing through PBS
1, PBS
2, PBS
3, and PBS
4, items
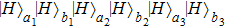
and
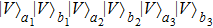
can make each of the output modes
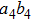
,
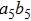
, and
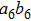
contain one photon. By selecting the six-mode case, they can obtain
with the probability of
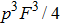
. On the other hand, with the probability of
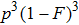
, states
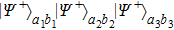
can be written as
After passing through PBS
1, PBS
2, PBS
3, and PBS
4, items
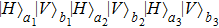
and
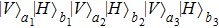
can make each of the output modes
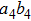
,
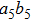
, and

contain one photon. By selecting the six-mode case, they can obtain
with the probability
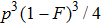
.
Next, we discuss states
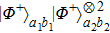 . If errors occurs, states
. If errors occurs, states
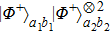 will become states
will become states
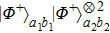 ,
,
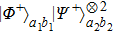 ,
,
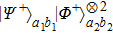 , and
, and
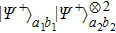 which we have described before. Interestingly, only two states
which we have described before. Interestingly, only two states
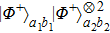 and
and
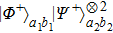 have the possibility to satisfy the six-mode case. For example, with the probability of
have the possibility to satisfy the six-mode case. For example, with the probability of
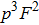 , states
, states
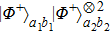 can be written as
can be written as
After passing through PBS
1, PBS
2, PBS
3, and PBS
4, only
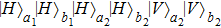
and

can satisfy six-mode case. By selecting six-mode case,

and
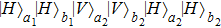
will both become the state
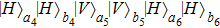
with the probability of
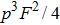
. With the probability of
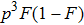
, states
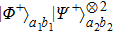
can be written as
After passing through PBS1, PBS2, PBS3, and PBS4, only items
and
can satisfy the six-mode case. Interestingly, by selecting the six-mode case,
and
both become
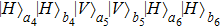
with the probability
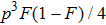
.
Therefore, from the states
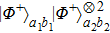 and
and
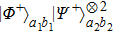 , they can obtain the states
, they can obtain the states
with the total probability
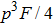
.
Similarly, the states
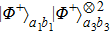 can be described in the same way. Because of errors, it will become four different states as
can be described in the same way. Because of errors, it will become four different states as
Only the states

and
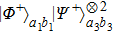
have the possibility to satisfy six-mode case. By selecting six-mode case, they can totally obtain
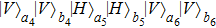
with the probability of
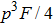
.
Moreover, if considering the states
 and
and
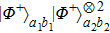 together, they can obtain the state
together, they can obtain the state
with the probability of
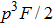
.
The other states
can be discussed with the same principle. If considering the states
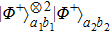
and
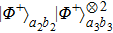
together, they can obtain the state
with the probability of

. If considering the states
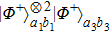
and
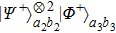
together, they can obtain the state
with the probability of
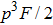
.
From the states
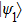 ,
,
 ,
,
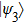 ,
,
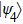 , and
, and
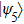 , after measuring the photons in spatial modes a5, b5, a6, and b6 in the basis
, after measuring the photons in spatial modes a5, b5, a6, and b6 in the basis
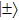 , states
, states
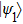 ,
,
 ,
,
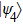 , and
, and
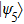 will become
will become
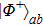 and
and
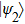 will become
will become
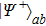 .
.
Finally, they can ultimately obtain a new mixed state
and the fidelity is
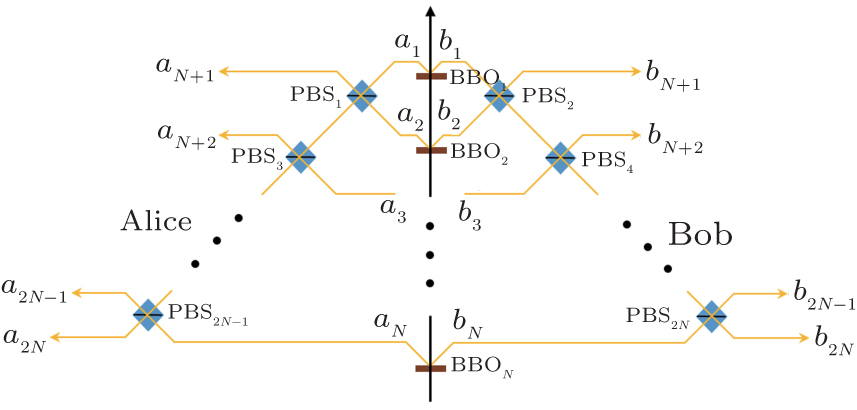
It is straightforward to extend this protocol to the EPP with N pairs of mixed states.
As shown in Fig. 3, the pump passes through N BBOs and creates the correlated photon pairs in spatial modes
 ,
,
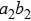 , …,
, …,
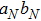 , respectively. Similar to the EPP with two pairs of mixed states and three pairs of mixed states described above, for the EPP with four pairs of mixed states, they select the eight-mode cases and obtain the new fidelity as
, respectively. Similar to the EPP with two pairs of mixed states and three pairs of mixed states described above, for the EPP with four pairs of mixed states, they select the eight-mode cases and obtain the new fidelity as
Generally, we can also obtain
Here
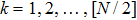
. If
N is odd, [
N/2] equals
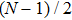
. Otherwise, it equals
N/2. Here

and
αk (

) is
Here
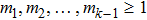 and they are all different positive integers which satisfy the condition
and they are all different positive integers which satisfy the condition
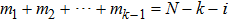 . Here we should iterate over all possible mi (
. Here we should iterate over all possible mi (
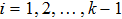 ) and sum over all possible cases.
) and sum over all possible cases.
We can also calculate the total success probability as
Here
P2,
P3,
PN are the success probabilities with two-copy, three-copy, and
N-copy purification.
4. Discussion and conclusionSo far, we have completely discussed this EPP. We mainly discussed the EPP for bit-flip error. Certainly, similar to Refs. [29] and [50], the phase-flip error can also be purified with the same principle, by adding the Hadamard operations to convert the phase-flip error to bit-flip error. In linear optics, the Hadamard operation can be implemented by quarter wave plate (QWP). It is interesting to calculate the fidelity of this EPP. As shown in Fig. 4, we calculated the new fidelity FN altered with the initial fidelity F. Here we let
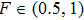 and N = 2, 3, 4 and 5 respectively. For example, if F = 0.55, we can obtain that
and N = 2, 3, 4 and 5 respectively. For example, if F = 0.55, we can obtain that
 and
and
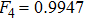 . In conventional EPPs,[29,50] we require the fidelity of initial mixed state to
. In conventional EPPs,[29,50] we require the fidelity of initial mixed state to
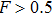 . In this EPP, we show that if
. In this EPP, we show that if
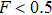 , we can also obtain a higher fidelity of mixed state.
, we can also obtain a higher fidelity of mixed state.
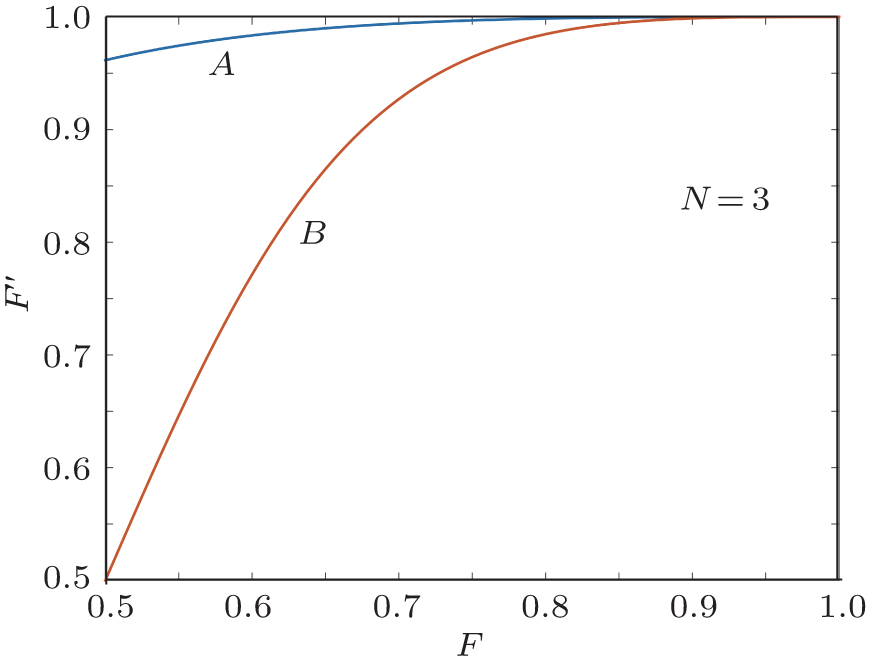
In Figs. 5 and 6, we calculated the purified fidelity in EPPs with two copies and three copies in Refs. [29] and [50], respectively. In Fig. 5, curve A represents the purified fidelity
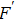 altered with the initial fidelity F in this EPP with two copies. Curve B represents the purified fidelity
altered with the initial fidelity F in this EPP with two copies. Curve B represents the purified fidelity
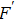 altered with the initial fidelity F in Ref. [29]. In Fig. 6, curve A represents the purified fidelity
altered with the initial fidelity F in Ref. [29]. In Fig. 6, curve A represents the purified fidelity
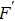 altered with the initial fidelity F in this EPP with two copies. Curve B represents the purified fidelity
altered with the initial fidelity F in this EPP with two copies. Curve B represents the purified fidelity
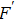 altered with the initial fidelity F in Ref. [50]. From both Fig. 5 and Fig. 6, we show that the SPDC source is not the obstacle but the advantage. Actually, in Ref. [30], they have realized the EPP with SPDC sources. In their experiment, if the initial fidelity is 3/4, they can obtain a higher fidelity 13/14, which is also larger than the theory value 9/10 with ideal entanglement sources.
altered with the initial fidelity F in Ref. [50]. From both Fig. 5 and Fig. 6, we show that the SPDC source is not the obstacle but the advantage. Actually, in Ref. [30], they have realized the EPP with SPDC sources. In their experiment, if the initial fidelity is 3/4, they can obtain a higher fidelity 13/14, which is also larger than the theory value 9/10 with ideal entanglement sources.
In Fig. 7, we calculated the total success probability altered with the initial fidelity F. We let p = 0.1. Curve a is the case of two-copy purification. Curve b is the case of three-copy purification, and curve c is the case of four-copy purification, respectively. We show that the success probability
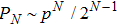 and it decreases with N. In EPP with linear optics, they should exploit the post-selection principle. After the success purification, the purified mixed state should also be detected and they cannot improve the fidelity by repeating the EPP. With multi-copy purification, though the total success probability is low, we can obtain a higher fidelity for perform the EPP for one step. Therefore, it is a trade off between success probability and fidelity. In order to realize the multi-copy EPP, we should let the pump pass through N BBOs to generate N pairs of mixed states simultaneously. Such cascaded entanglement sources have been widely realized in current experiment, such as multi-photon entanglement generation,[53] quantum teleportation of multiple degrees of freedom of a single photon,[54] experimental Greenberger–Horne–Zeilinger-type six-photon quantum nonlocality,[55] and so on.
and it decreases with N. In EPP with linear optics, they should exploit the post-selection principle. After the success purification, the purified mixed state should also be detected and they cannot improve the fidelity by repeating the EPP. With multi-copy purification, though the total success probability is low, we can obtain a higher fidelity for perform the EPP for one step. Therefore, it is a trade off between success probability and fidelity. In order to realize the multi-copy EPP, we should let the pump pass through N BBOs to generate N pairs of mixed states simultaneously. Such cascaded entanglement sources have been widely realized in current experiment, such as multi-photon entanglement generation,[53] quantum teleportation of multiple degrees of freedom of a single photon,[54] experimental Greenberger–Horne–Zeilinger-type six-photon quantum nonlocality,[55] and so on.
In conclusion, we have discussed the multi-copy EPP with practical SPDC sources. This EPP requires linear optics to complete the task and it is feasible in current experiment condition. Moreover, compared with the EPP with ideal entanglement sources, we show that the SPDC source is not an obstacle but an advantage and can benefit the purification. As the ideal entanglement sources are not available, this EPP may be useful in long-distance quantum communication.