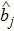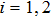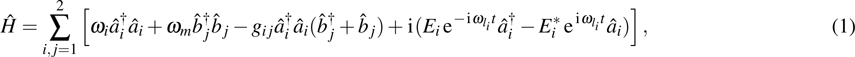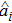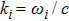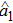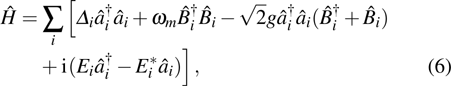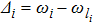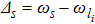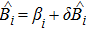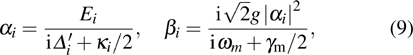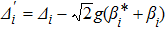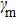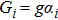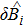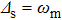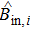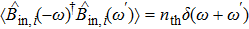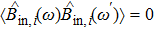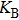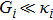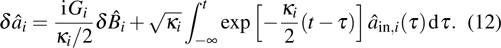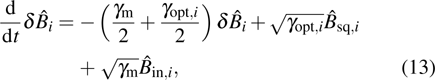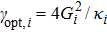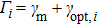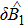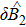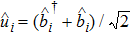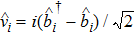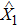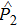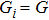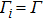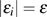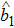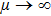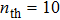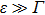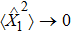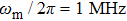Generating EPR-entangled mechanical state via feeding finite-bandwidth squeezed light
1. IntroductionRapid advancement of microfabrication techniques including ground-state cooling,[1,2] strong optomechanical coupling,[3,4] optomechanically induced transparency (OMIT)[5–7] in cavity optomechanics promotes the control and measurement of massive mechanical oscillators as well as further applications in ultrahigh-precision sensing[8–10] and quantum information processing (QIP),[11–15] and enables tests of fundamental quantum physics.[16] Of particular fundamental interest is to investigate the entanglement in macroscopic scale, which is critical for a deeper understanding of the boundary between the classical and quantum world. Since entanglement is a distinguishing feature of quantum mechanics, where measurements of one system appear to determine the state of the other for a bipartite entangled state, and the peculiar property becomes a resource for constructing hybrid QIP systems exceeding the classical information processing limits.[17] Therefore, the possibility of entangling two mechanical oscillators has been widely investigated, such as exploring the ponderomotive force,[18,19] injecting entangled fields,[20,21] modulating the optomechanical coupling,[22] and using an entanglement-swapping protocol,[23] etc.
In particular, continuous-variable (CV) Einstein–Podolsky–Rosen (EPR) entanglement represents a figure of merit for characterizing the efficacy of entanglement-based CV quantum information protocols, including quantum key distribution (QKD), quantum teleportation, and entanglement swapping.[24] Continuous-variable EPR entanglement can be directly generated via nondegenerate optical down conversion processes,[25] and an alternative approach is to combine two single-mode position and momentum squeezed states at a 50:50 beam splitter (BS),[26] which can be extended to generate the EPR entangled state of massive systems. Hence methods of generating mechanical squeezing can be exploited to generate mechanical EPR entanglement, such as reservoir engineering with the use of two-tone driving,[27] employing a parametric amplifier (PA) inside the optomechanical cavity,[28] ponderomotive squeezing by Coulomb interaction,[29] feeding the finite-bandwidth squeezed reservoir,[30] as well as with the help of a nitrogen-vacancy (NV) center or quantum dots (QDs).[31–33] Moreover, entanglement of macroscopic oscillators is fragile to the unavoidable decoherence and dissipation caused by the surrounding thermal noise. Luckily besides squeezing mechanical motion, squeezed light and PA can help to more efficiently cool the motion of a macroscopic mechanical object below the quantum limit.[28,34]
Here we propose to exploit the combined effects of optomechanical squeezing and mechanical cooling to generate a steady EPR-entangled state of mechanical oscillators in a ring resonator. We consider the system consisted of two membranes located inside a ring resonator, and both the clockwise (CW) and counter-clockwise (CCW) travelling-wave modes are pumped by lasers and finite-bandwidth squeezed lights. Via carefully tuning the equilibrium position of two membranes, CW and CCW modes can couple to the center-of-mass (COM) motion and relative motion of oscillators respectively, which corresponds to a 50:50 BS mixing of mechanical modes. Furthermore, via employing the red-detuned driving laser and tuning the central frequency of squeezing field blue detuned from the driving laser with a mechanical frequency, the squeezing property of squeezed light can be perfectly transferred to the mechanical motion in the rotating-wave approximation (RWA). Therefore, the BS mixing modes can be position and momentum squeezed by feeding the appropriate squeezed lights respectively, and the EPR-entangled mechanical state is achievable. We focus on the weak optomechanical coupling regime and adiabatically eliminate the cavity field to achieve the explicit expression for EPR entanglement. We find that the entanglement can be enhanced with the increasing bandwith of squeezed lights, and maximum squeezing is obtained in the squeezed white noise limit. Moreover, the mechanical thermal noise can decrease the entanglement, and the critical thermal occupation where the entanglement disappears is also discussed.
The paper is organized as follows. In Section 2, the physical system is introduced. In Section 3, the generation of mechanical EPR-entangled state is derived, and the influence of the bandwidth of squeezed light and mechanical thermal noise on the entanglement is analyzed, and finally the conclusion is drawn.
2. Description of physical modelWe consider the system comprising of two vibrating membranes located inside a ring cavity, where the CW and CCW travelling-wave modes are pumped by two independent laser fields accompanied with two finite-bandwidth squeezed lights through two separated partially transmitting mirrors, as shown in Fig. 1.
The membranes vibrate around the equilibrium positions  (j = 1,2) with the identical frequency ωm and effective mass m, and mechanical modes are characterized by annihilation operators
(j = 1,2) with the identical frequency ωm and effective mass m, and mechanical modes are characterized by annihilation operators 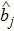 . The CW and CCW optical modes described by annihilation operators
. The CW and CCW optical modes described by annihilation operators  (
(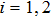 ) with frequencies ωi couple to the vibrating membranes via optomechanical interactions, and the Hamiltonian of the system is given by
) with frequencies ωi couple to the vibrating membranes via optomechanical interactions, and the Hamiltonian of the system is given by
where
Ei is the laser driving strength at frequency

. Optomechanical coupling strength between
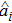
and

is similar to the “membrane-in-the-middle” arrangement and characterized by
[35]
where
L is the length of resonator, and
with
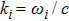
the wave number of
i-th cavity mode,

the
j-th membrane intensity reflection coefficient for the
i-th cavity mode. With a suitable choice of system parameters, such as the equilibrium position of membranes, it is possible to assume that the optomechanical coupling rates are equal in strength with different phases,
[36,37] i.e.,
Therefore, cavity mode 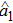 couples to the COM motion of membranes and
couples to the COM motion of membranes and  couples to the relative motion of membranes, as discussed in Ref. [38].
couples to the relative motion of membranes, as discussed in Ref. [38].
By now we introduce the normal modes which are the symmetrical and antisymmetrical combinations of motion of two membranes
which correspond to the BS mixing of two mechanical modes. In the rotating frame of the laser’s frequency, the Hamiltonian becomes
where the detunings are
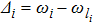
. In parallel to the coherent driving, each cavity mode is subjected to an independent squeezed field with damping rate
κi, which is the squeezed output field of an optical parametric oscillator (OPO) below the threshold. The correlation spectra are in the form of minus/sum of two Lorentzian functions and expressed as
[39]
where
εi characterizes the nonlinearity of OPO,
γi is the damping rate of OPO cavity,

and

are the bandwidths of the squeezed light,
ηi is the ratio between the transmitting rate at the output port and the damping rate, and
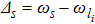
is the detuning between central frequency of squeezed light
ωs and the driving laser frequency.
We investigate the optomechanical interaction with the linearization procedure by employing a large laser driving to enhance the coupling, and the cavity and mechanical modes are written as a sum of coherent and quantum fluctuation parts, i.e.,  ,
, 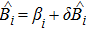 , where
, where  and
and  are the average amplitudes and
are the average amplitudes and  and
and  are the quantum fluctuation operators. The mean values obey the equations
are the quantum fluctuation operators. The mean values obey the equations
from which we can achieve the steady-state mean values
with the redefined detuning
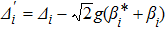
and the mechanical damping rate
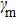
. The linearized Hamiltonian becomes
where the effective optomechanical coupling strength is
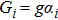
, and
αi can be real by tuning the phase of the driving laser.
3. Preparation of EPR mechanical entanglementOur motivation for generating an EPR-entangled mechanical state is to combine two single-mode position and momentum squeezed states at a 50:50 BS,[26] where the BS mixing is already obtained in Eq. (5). Therefore, we will focus on the discussion of squeezing properties of normal modes 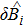 , which is realizable by transferring the squeezing from the cavity field to mechanical motion. The efficient transfer of squeezing should fulfill two conditions: (i) realization of the BS-type optomechanical interaction via employing a red-detuned driving laser, i.e.,
, which is realizable by transferring the squeezing from the cavity field to mechanical motion. The efficient transfer of squeezing should fulfill two conditions: (i) realization of the BS-type optomechanical interaction via employing a red-detuned driving laser, i.e.,  , and (ii) the central frequency of squeezing field blue detuned from driving laser with a mechanical frequency,[40] i.e.,
, and (ii) the central frequency of squeezing field blue detuned from driving laser with a mechanical frequency,[40] i.e., 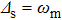 . In the rotating frame of mechanical frequency and making use of RWA under the condition
. In the rotating frame of mechanical frequency and making use of RWA under the condition  , the quantum Langevin equations can now be written in the form
, the quantum Langevin equations can now be written in the form
where
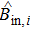
is the input mechanical thermal noise and obeys the correlations
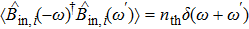
,
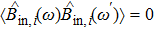
. Here
is the average thermal occupation number of the mechanical mode,
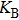
is the Boltzmann constant, and
T is the temperature of environment.
Here we focus on the weak optomechanical coupling regime 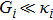 , where the cavity mode would reach fast to the steady state on the time scale of optomechanical coupling. Thus the cavity mode can be adiabatically eliminated which equals to
, where the cavity mode would reach fast to the steady state on the time scale of optomechanical coupling. Thus the cavity mode can be adiabatically eliminated which equals to
Via substituting the expression into Eq. (11), the effective equation for the motion of the oscillator becomes
where
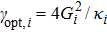
is the cavity-induced damping rate in the resolved-sideband limit,
[41,42] and the total damping rate is
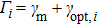
. The mechanical motion is surrounded by two parts of noise, where
is the accompanying finite-bandwidth squeezed noise transferred from the cavity field, which corresponds to the non-Markovian Langevin force on mechanical motion.
In order to solve Eq. (13), it is convenient to perform the Fourier transform[43]
and the solution in the frequency domain can be obtained as
In addition, the squeezing of mechanical motion is characterized by the variances of the generalized quadrature operator, which is defined in the frequency domain as
It represents the position operator  for θ = 0 and the momentum operator
for θ = 0 and the momentum operator  for
for  . By the aid of the correlations of the noise source in Eq. (7), the spectrum of quadrature operator defined by
. By the aid of the correlations of the noise source in Eq. (7), the spectrum of quadrature operator defined by
becomes
and the steady-state mean square of quadrature fluctuations in the time domain is determined by the relation
[43]In order to achieve the entanglement between the mechanical modes  and
and  , we should make the BS-type mixing of modes
, we should make the BS-type mixing of modes 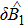 and
and 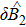 position and momentum squeezed respectively, and the measurement of entanglement is indicated by the degree of squeezing. The explicit criterion for EPR entanglement of
position and momentum squeezed respectively, and the measurement of entanglement is indicated by the degree of squeezing. The explicit criterion for EPR entanglement of  and
and  is characterized by the correlation of observables of quadrature operators
is characterized by the correlation of observables of quadrature operators 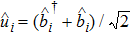 and
and 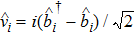 , which is the two-mode squeezing condition and fulfills[44]
, which is the two-mode squeezing condition and fulfills[44]
Therefore, to achieve the optimal entanglement we should obtain the maximum squeezing indicated by Eq. (17), where ε1 should be real and positive for the position operator 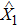 of
of  , and ε2 should be real and negative for the momentum operator
, and ε2 should be real and negative for the momentum operator 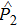 of
of  . Moreover, it is feasible to assume the other parameters of two mechanical oscillators are identical via employing the symmetric driving, i.e.,
. Moreover, it is feasible to assume the other parameters of two mechanical oscillators are identical via employing the symmetric driving, i.e., 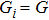 ,
,  ,
, 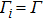 ,
,  ,
, 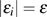 ,
,  , and we have the analytical results
, and we have the analytical results
The criterion for EPR entanglement becomes  . Due to the weak optomechanical coupling compared to the cavity damping rate we have
. Due to the weak optomechanical coupling compared to the cavity damping rate we have  , and the strong cavity-induced mechanical cooling rate compared to high-Q mechanical oscillator
, and the strong cavity-induced mechanical cooling rate compared to high-Q mechanical oscillator  , the variance can be further simplified as
, the variance can be further simplified as
which is contributed by the squeezed light, vacuum fluctuation and cavity-induced suppression of thermal noise, respectively.
The EPR entanglement of modes 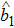 and
and  is achievable when
is achievable when  . For squeezed light produced from the ideal single-sided OPO cavity,
. For squeezed light produced from the ideal single-sided OPO cavity,  . In Fig. 2 we plot the EPR entanglement as a function of the damping rate of the OPO cavity with the parameters applied in Ref. [40]. The damping rate connects to the bandwidth of squeezed light, and figure 2 shows that the increase of bandwidth will improve the mechanical entanglement. Especially, in the squeezed white noise limit parameters
. In Fig. 2 we plot the EPR entanglement as a function of the damping rate of the OPO cavity with the parameters applied in Ref. [40]. The damping rate connects to the bandwidth of squeezed light, and figure 2 shows that the increase of bandwidth will improve the mechanical entanglement. Especially, in the squeezed white noise limit parameters
with squeezing bandwidth

,
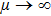
, the variance becomes
For example, with the parameters given in Fig. 2, E = 0.184 for 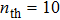 , which is consistent with the numerical result.
, which is consistent with the numerical result.
However, the unavoidable mechanical thermal noise can decrease the squeezing and thus EPR entanglement, as shown in Fig. 2. There exists a critical thermal number corresponding to E = 1, which is achieved from Eq. (20) as
When the initial thermal number is below  for a given squeezed light, two mechanical modes are EPR entangled, and otherwise not entangled.
for a given squeezed light, two mechanical modes are EPR entangled, and otherwise not entangled.
Moreover, the maximum squeezing of the output field of the OPO cavity occurs at the threshold  , and then equation (20) gives
, and then equation (20) gives
which indicates the maximum squeezing
in the limit
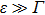
. The squeezing is mainly affected by the unavoidable mechanical thermal noise. With the strong cavity-induced mechanical cooling,
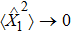
, and mechanical modes approach an ideal EPR entanglement.
4. ConclusionIn conclusion, following the proposal of the generation of an EPR entanglement state by combining two single-mode position and momentum squeezed states at a 50:50 BS, we study the generation of the EPR-entangled mechanical state of two vibrating membranes in a ring resonator, where CW and CCW travelling-wave modes are driven by lasers and finite-bandwidth squeezed lights. Via tuning the location of membranes, CW and CCW couples to the symmetric and antisymmetric combination of mechanical modes, corresponding to a 50:50 BS mixing. Moreover, for each cavity mode via employing a red-detuned driving laser and tuning the central frequency of squeezing field blue detuned from the driving laser with a mechanical frequency, the squeezing property of squeezed light can be perfectly transferred to the mechanical motion in the RWA. Thus, the BS mixing modes can be position and momentum squeezed by feeding the appropriate squeezed lights, and the EPR-entangled mechanical state is achievable. In addition, cavity-induced mechanical cooling can significantly suppress the influence of thermal noise to achieve an ideal entanglement.