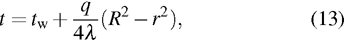1. IntroductionThere is an increasing demand for ultra-clean metallic powders used in producing advanced materials for aerospace, automotive, biomedical, three-dimensional (3D) printing and other applications.[1] Direct melting of an electrode by induction heating is a contactless technique suitable for reactive high melting temperature alloys. Producing reactive high melting temperature alloy powders requires a contactless technique avoiding direct contact with refractory crucibles. Electrode induction-melt inert gas atomization (EIGA) is a well-known ceramic-free technology for preparing the ultra-clean metal powders.[2]
Recently, the Germany ALD Vacuum Technology Company developed an EIGA technique for preparing the reactive high melting point titanium, niobium, and zirconium alloy powders.[3] In this technique, powder particle sizes range from
to
. Nickel-based superalloy is mainly used for fabricating the important high temperature parts including the turbine disk, turbine baffle, compressor disk, and other critical components.[4–8] Ceramic inclusions in powder metallurgy (PM) superalloy can promote fatigue crack initiation and thus accelerate the crack propagation under certain conditions.[9–11] In this case, the ultra-clean nickel-based superalloy powder is critical for PM superalloy components.[12–21] However, there are no reports on the preparation of nickel-based superalloy powders by the EIGA process. Comparison among titanium, niobium and zirconium alloys, nickel-based superalloy electrodes showed different melting characteristics. Thus, it is difficult to carry out an induction melting in EIGA equipment, since more alloying elements were added in superalloy to produce the desired product. Consequently, physical and chemical properties of the electrode materials became complicated with induction heating. For example, the melting viscosity of a nickel-based superalloy is high and the magnetic permeability of the material is low.[22] Since 2010, we have developed a Chinese-EIGA apparatus for preparing the ultra-clean nickel-based superalloy powders. The induction melting process is complex, however, numerical simulations are a powerful tool for studying the induction melting process. For instance, Valdis Bojarevics, et al.[1,23,24] used the commercial software COMSOL Multiphysics
to investigate the complex interaction between the electromagnetic and thermal fields in a titanium alloy.
In this paper, for preparing the ultra-clean nickel-based superalloy powders, the consecutive electrode induction melting of superalloy electrode is studied in numerical simulations and experiment. The key issues for consecutive electrode induction melting of superalloy include the design of the induction coil, the distance between the coil and metal pieces, and the influence of coil output power on magnetic field and melting temperature.
2. Experiment2.1. Induction melting of nickel-based superalloyA nickel-based FGH4095 superalloy electrode was prepared by vacuum induction melting and vacuum arc remelting with the following composition (wt%): Cr (12.24), Co (8.54), Nb (4.49), Mo (3.65), Al (3.525), W (3.46), Fe (0.43), Si (0.07), Mn (0.04), Zr (0.03), Ta (0.01), C (0.06), and Ni-base. Each electrode had dimensions of Φ40 × 500 mm3. The parameters for the induction coil included one working frequency of 400 kHz with an output power of 100 kW, and the second working frequency of 40 kHz with an output power of 120 kW. In the induction melting process, the superalloy electrode was immersed in a conical induction coil. Through introducing a high frequency electromagnetic field into the electrode tip, the liquid metal fluid was then formed.
2.2. Numerical simulationThe numerical simulation electrode induction melting method used included the following steps: (i) choosing the alternating current and heat transfer module in the software COMSOL Multiphysics
; (ii) using the 2D axisymmetric method to solve a complex electrode induction melting process. The second step also allowed the investigation of the electromagnetic field near the electrode and thermal field effects on the fluid flow with free surface. Considering the physical model and boundary condition problems, some parameters such as air flow, electrode and induction coil were selected as shown in Fig. 1. Parameters including electrode diameter, electrical conductivity, thermal conductivity, density, heat capacity at constant pressure, relative permeability, induction coil frequency, output power, and the distance between the coil and the electrode were set to be 40 mm, 67 S/m, 14 W/(m
K), 8030 kg/m3, 413 J/(kg
K), (400 kHz/40 kHz), (100 kW/120 kW), and 9 mm, respectively.
3. Results and discussion3.1. Consecutive induction melting experiment at different frequenciesFigure 2(a) shows the initial profile of a superalloy electrode immersed in a conical induction coil. Figure 2(b) shows the melting experiment with a frequency of 400 kHz at 100 kW power. The data indicate that no consecutive induction melting fluid is detected, but melted droplets are formed with a diameter of about 5 mm. It indicates that the frequency is too high to melt enough surface materials to form consecutive induction melting fluid. On the contrary, consecutive induction melting fluid metal flow, with a diameter of about 7 mm, is formed with a frequency of about 40 kHz at 120 kW as shown in Fig. 2(c). The different results indicate the critical role of frequency in the consecutive induction melting process. In fact, the consecutive induction melting process is so complex that it may relate to complex interaction of the electromagnetic field, alloy element compositions, magnetic property of material and fluid melt viscosity. So, the process is difficult to study in experiment directly. An attempt is made to understand the complex process and describe the intrinsic physical properties in consecutive induction melting by numerical simulation as discussed in the next sections.
3.2. Physical principle of induction meltingWhen the slowly rotated and fed superalloy electrode was lowered into the conical induction coil with alternating current, a time-varying current could induce a varying magnetic field. In this setup, an equal but opposite electric current could be generated on the surface of the superalloy electrode, the surface of the electrode will be quickly heated up to its melting point. Figure 3 shows the schematic of the induction melting process. The melting physical principle was based on the well-known Joule-Lenz law:
where
I is the effective current (in unit A),
R the resistance of the metal piece (superalloy electrode) (in unit Ω), and
t the melting time (in unit s).
In the induction melting process, the control of the rotating and feeding electrode was an important issue. Factors including electrode vertical feed rate, melting temperature and thermodynamic parameters are described by the continuity, momentum and energy equations as follows:
where
ρ is the liquid metal flow density (in units kg/m
3),
u the electrode vertical feed rate (in units m/s),
p the ambient pressure (in unit Pa),
T the free surface temperature (in unit °C),
the reference temperature (in unit °C),
Q the inductive heating energy (in unit J),
k the thermal conductivity (in units W/(m
K)),
β the dynamic viscosity (in units m
2/s),
the specific heat capacity (in units J/(kg
K)), and the Hamiltonian operator.
The entire induction melting process can be described as follows: by alternating current flowing through the induction coil, an alternating magnetic field can be generated, resulting in an eddy current induced on the electrode surface. In the melting process, the melting fluent rate and efficiency are determined by the physical property of the workpiece. The macroscopic magnetic field can be described by the Maxwell equations as follows:
where
H refers to the magnetic field intensity (in units A/m),
J the current density (in units A/m
2),
D the electric flux density (in units C/m
2),
E the electric intensity (in units V/m),
B the magnetic flux density (in unit T),
ρ the electric density (in units C/m) and
t the time (in unit s). These expressions describe the relationship among electromagnetic field quantities (
H,
D,
E,
B) in some domain, as a function of field source electric charge and electric current.
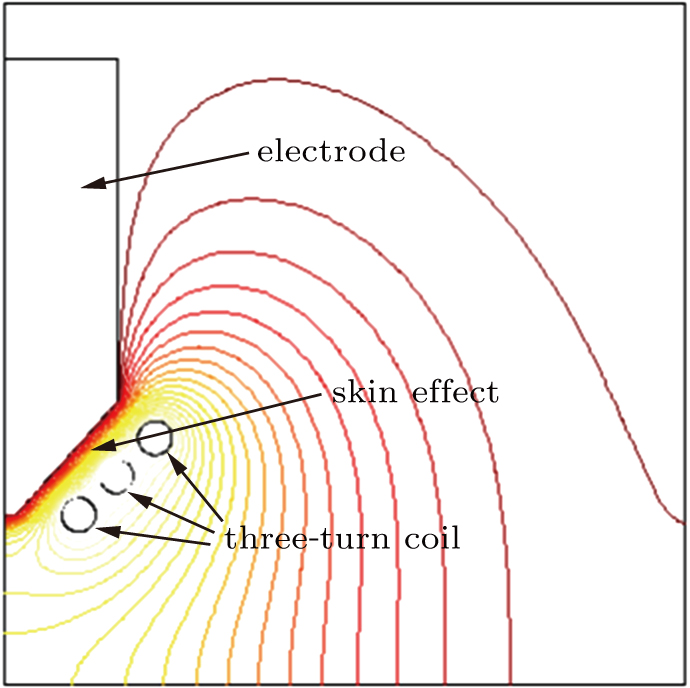
3.3. Design of the conical induction coilThe coupled design of the superalloy electrode tip shape and conical induction coil is critical for the induction melting process. Figure 4 shows the details of the superalloy electrode tip shape and induction coil in a consecutive induction melting experiment described in Subsection 3.1. The coupled design is further verified using the finite element software COMSOL Multiphysics
. As shown in Fig. 5, the electromagnetic field energy concentrates on the conically shaped electrode, which is immersed in a tapered coil. The current flows in a thin skin and concentrates on the inner surfaces of the coil due to magnetic flux confinement. Figure 6 shows the profile for the melted tip shape of a nickel-based superalloy electrode. The normal, conically shaped, solid core is formed with the angle kept at 45° with a frequency of about 40 kHz at 120 kW.
3.4. Influence of coil frequency on induction meltingAs indicated in Subsection 3.1, the output power and frequency of the induction coil are 100 kW/400 kHz, and 120 kW/40 kHz, respectively. Under these conditions the corresponding magnetic flux density and magnetic field values are calculated to be 0.29 T/2.38 × 105 A/m, and 0.28 T/2.3 × 105 A/m, respectively. Figures 7 and 8 reveal the magnetic flux density and magnetic field distribution. These data indicate that the frequency of effective current influences magnetic flux density only minimally. The change in frequency affects the eddy current distribution in the workpiece and depth of heating from the surface. While the eddy current and effective current are always in opposing directions, the number of magnetic streamlines perpendicular to the unit-surface do not increase the electromagnetic field. The increasing of frequency seems to speed up changing the direction of the magnetic field. At a known melting temperature, the relative permeability and electric conductivity of the workpiece are known, in which the eddy current is in a thin skin also referred to as the depth of fusion. It is expressed as
 | |
in the above expression,
f is the frequency of the coil (in unit Hz),
μ the relative permeability of the workpiece (in units H/m), and
σ the electric conductivity of the workpiece (in units S/m).
High frequency current is applied to the induction coil, which makes the eddy current density distribution varied from the surface to the core. Thus, the increasing of the coil frequency results in the eddy current from the core, the eddy current moves out of the core and concentrates in the conical surface. The current flow is confined to a thin skin and concentrates in the inner surface of the induction coils where the contours are tightly bunched. The highest values of magnetic flux density and magnetic field are found in the space enclosed by the bottom coil turn, which has the smallest radius and leads to higher flux confinement. By adjusting the frequency of effective current, the eddy current distribution from the surface to core is made to increase or decrease. The eddy current distribution can be exponentially expressed as
where
I0 is the original eddy current density at the surface (in units A/m) of the workpiece,
Ix the eddy current density at position
x (in unit m) for a given depth from the workpiece surface (in units A/m). Given the known nickel-based superalloy characteristics, it seems that the ultra-high frequency eddy currents counteract each other, possibly in a thin skin.
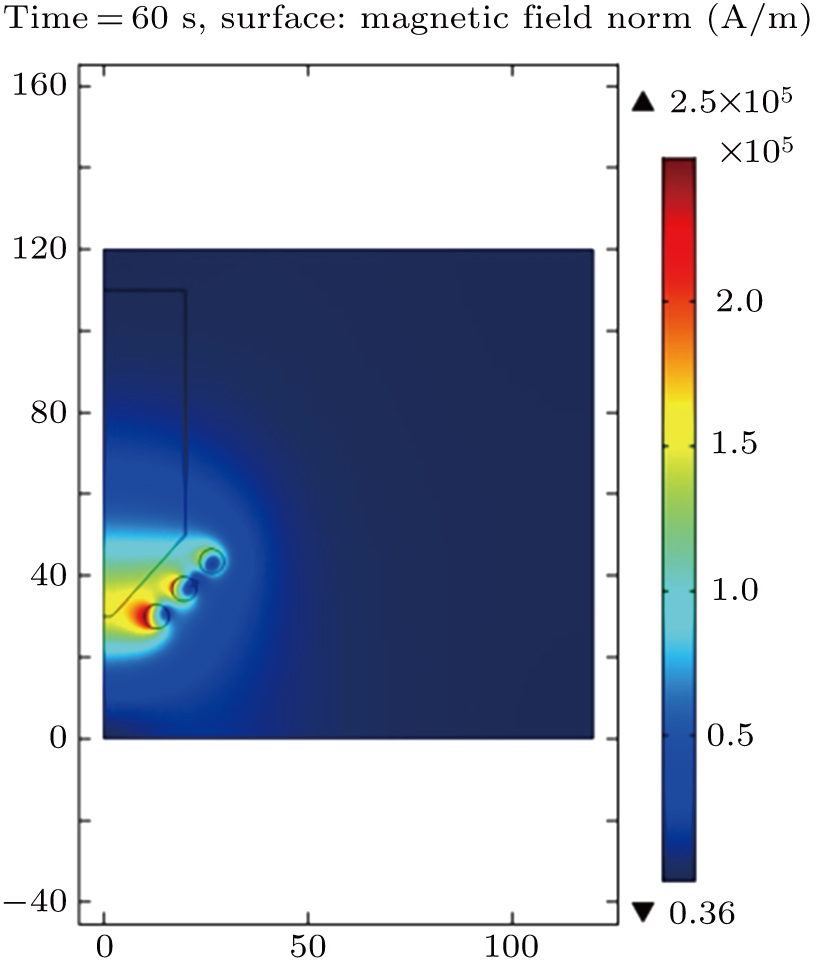
3.5. Influence of output power on induction meltingIn the superalloy melting process, it is thermodynamically favorable to take full advantage of induction coil power to release electrical energy in the conical surface. This also proves to be the superalloy electrode rapid melting dynamic condition. The nickel-based superalloy is conducting electrically, while the output power depends mainly on the resistance of the superalloy electrode (
). Figures 9 and 10 show the distributions of magnetic field intensity of the operation frequency 400 kHz/40 kHz and output power 100 kW/120 kW. These figures indicate that the increasing of the output power strengthens the intensity of the magnetic field. The magnetic field value at output power 100 kW is 2.38 × 105 A/m, and the magnetic field value at output power 120 kW is 2.5 × 105 A/m. The magnetic field is distributed homogeneously on the superalloy conical surface and the eddy current flows in the thin skin.
The high frequency induction coil current can induce the current layer covering the electrode surface; but is spatially non-uniform along the surface. Figure 11 shows the temperature distribution in the molten layer at a frequency of 400 kHz and an operation power of 100 kW. The melting temperature is observed at 1730 K (1467 °C) under these conditions. For this system, the superheating was relatively low, and the liquid film thickness temperature is slightly above the melting temperature. The feedstock electrode melting rate is slow. The simulation result under the condition of a frequency of 400 kHz and an operation power of 100 kW accords with the experimental result. Figure 12 shows the melting temperature distribution of alternating current at a frequency of 40 kHz and the output power of 120 kW. The melting temperature is observed at 2020 K (1874 °C) and melted liquid flow becomes consecutive. In this experiment, the electrode is fed into an induction coil. After a few seconds, the fully coupled electromagnetic, thermal and flow fields evolve, and a quasi-steady molten liquid metal flow forms. The liquid metal stream is mainly downward due to the joint action of gravity and inertia forces. The thermal center of the electromagnetic field concentrates on the induction coil minimum diameter.
Finally, the simulation results accord well with the experimental results. The induction melting temperature is lower under the condition of an alternating current frequency of 400 kHz and output power of 100 kW. The induction melting temperature is above melting point under the condition of an alternating current frequency of 40 KHz and output power of 120 kW.
3.6. Thermal conduction of workpieceIn the superalloy electrode induction melting process, thermal conduction of the workpiece must be considered. Thermal conduction occurs through the transfer of energy (in the form of heat) arising from temperature differences between adjacent parts of the workpiece. The nickel-based superalloy is a high density material, so the thermal conduction causes thermal loss on the electrode. Figure 13 shows the thermal conduction on the superalloy electrode. The workpiece surface layer induces an eddy current, and as the current passes through the resistance presented by the superalloy, heat evolves in the superalloy skin layer. Due to metallic material possessing thermal and electrical conductivities, some heat diffuses in the radial direction with respect to the workpiece core. The heat supplied presents favorable thermodynamic conditions and is beneficial to superalloy melting. Thermal conduction that occurs in the axial direction generates heat loss on the electrode. Figure 14 shows the radial temperature distribution, indicating that the surface layer temperature is higher. Therefore, it is a non-contact method of induction melting: the heat develops from the eddy current, and is highest at the electrode surface layer and lowest at its center. In the process of inductively melting superalloy, a chemical reaction in the superalloy does not occur. Thus, it is assumed that there are non-inner heat source materials. Given a superalloy electrode length of L and a diameter of R, the electrode length is much longer than the diameter. The thermal conduction and temperature distribution in the cross-sectional area of the conical part of the electrode are expressed by the following equations:
 | |
 | |
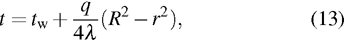where
t is the inner point temperature (in unit °C) of the conically shaped solid core,
r (in unit m) the corresponding radius,
the conical surface temperature (in unit °C),
λ the thermal flux of superalloy (in units W/m
°C), and
q the thermal flux (in units W/m
2).
