† Corresponding author. E-mail:
Thermal emission is often presented as a typical incoherent process. Incorporating periodic structures on the tungsten surface offers the possibility to obtain coherent thermal emission sources. Here we illustrate grating as an example to examine the influence of the geometric parameters on the thermal emission properties. It is found that for very shallow gratings, only surface plasmon polariton (SPP) modes can be excited and the emission efficiency is closely related with the filling factor. When the ratio of the depth to period of the grating is in the range from 1/20 to 1/2, the field between the adjacent corners can be coupled to each other across the air gap for the filling factor larger than 0.5 and produce a similar resonance as in an air rod. Further increase of the grating depth can cause the groove of the grating forming metal–insulator–metal (MIM) structures and induce surface plasmon standing wave modes. Our investigations will not only be helpful for manipulating thermal emission properties according to applications, but also help us understand the coupling mechanism between the incident electromagnetism waves and gratings with different parameters in various research fields.
Due to their unique properties to confine light in an extremely small area and potential applications in various fields of nanometer science and technology, surface plasmon polaritions (SPPs) have attracted tremendous interests in these last few decades.[1–5] They cannot be excited directly by incident electromagnetic waves on flat metal surfaces because of the momentum mismatch between the incident waves and SPPs. To compensate the momentum, a prism, a grating, or a defect is required on the metal surface. Utilizing a grating to afford an extra wavevector to compensate the momentum is one of the most widely applied methods.[6]
In contrast to lasing,[7,8] thermal emission is a typical incoherent process.[9] Obtaining controllable thermal emitting sources in the midinfrared spectrum range has been one of the important tasks in photonics technology.[10] When very shallow grating structures are introduced into the metal surfaces, spatially and temporally coherent thermal emission sources can be realized by exciting SPPs.[11–13] For example, we have proposed a two-dimensional orthogonally crossed shallow grating to produce an orthogonally-polarized dual wavelength radiation from a tungsten thermal source.[14] On the other hand, if we incorporate very deep gratings into the metal surfaces, microcavity modes can be excited and coherent thermal emission sources can be obtained.[15–18] In most of the related research, however, only very shallow (the height h being less than a twentieth of the period a) or very deep gratings (
In this paper, we investigate the evolution process of the emission properties with the filling factor and the depth of the tungsten gratings. It is found that the influence of the depth and the filling factor is correlated as they are changed. When the ratio between the depth and the period is less than 1/20, only SPPs can be excited and the influence of the filling factor is enhanced with an increase of the depth. When the ratio is between 1/20 and 1/2, the resonant wavelength of SPPs red-shifts at first with the increase of the filling factor due to the increase of the effective refractive index. When the filling factor is increased to be larger than 0.7, the field between the two adjacent corners of the grating starts to be coupled. The air gap under excitation exhibits a similar resonance as in an air rod,[19] which blue-shifts with the increase of the filling factor. When the ratio between the depth and the period is larger than 1/2, besides SPPs and air gap resonances, surface plasmon standing wave modes can be excited due to the formation of the waveguide of the grating wall–air–wall, which can be regarded as a metal–insulator–metal (MIM) structure. The influence of the geometric parameters on the thermal emission properties can not only provide us with direct information on how to choose appropriate parameters for thermal emission sources in different applications, but also help us understand the coupling mechanism between the incident electromagnetic waves and gratings with different parameters in various research fields.
The schematic of the grating is shown in Fig. 
 |
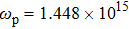
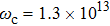
 | Fig. 1. (color online) Schematic of the simulated 1D tungsten grating. The geometry of the grating is defined by its period (a), width of the ridge (w), and groove depth (h). |
In the simulations, the thickness of the substrate is set as 500 nm, which is much larger than the skin depth of tungsten (about 20 nm), thus no light can penetrate and 









For a flat air–material interface, the surface plasmon wavevector propagating along the x direction, 



 |
 |



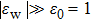



 |
Thus the resonant wavelength 

 |
As the emittance for higher order mode (j > 1) is much lower than that from the first order (j = 1),[14] we will mainly concentrate on discussing the emission at j = 1 for SPPs in the rest of the paper.
We choose the period of the tungsten grating a to be 4 μm to illustrate the influences of other geometric parameters on the thermal emission properties. Similar results could be obtained for other periods. The grating depth h is divided into three ranges based on its relationship with the period: h/a ≤ 1/20, 1/20 < h/a < 1/2, and h/a ≥ 1/2.
When h/a ≤ 1/20, the grating is very shallow. The bulge part (ridge) of the grating can be regarded as a perturbation although it affords the extra wavevector to excite SPPs. We choose h = 0.1 μm and 0.2 μm as two examples to examine the influence of the filling factor. Figure
From the right panel field map, it can be seen that the electric field is localized close to the grating interface (air side) and attenuates away from the interface at resonance. All the vertical white dashed lines drawn in the field maps are guides for eye and arranged with equal transverse distance. We can observe that along the direction parallel to the grating plane, the field intensity located at each vertical white dashed line is similar. The periodicity of the field intensity distribution suggests the excitation of the propagating SPPs.
When h/a is in the range from 1/20 to 1/2, the grooves of the grating can be regarded as cavities.[5,25,26] We choose the grating depth h = 0.3 μm, 0.6 μm, 1.0 μm, and 1.6 μm as examples to analyze the influence of the filling factor. A series of emission spectra with different filling factors and grating depths are plotted in Fig.
Firstly, we select the geometric parameters h = 0.6 μm and f = 0.3, 0.5, 0.6, 0.7, 0.9. As can be seen in Fig.
 | Fig. 4. (color online) Emissivity spectra (left column) and the corresponding field intensity distributions (right column) at different filling factors for h = 0.6 μm. |
When f < 0.5, the interaction between the two corners of the same ridge is dominant. Under this situation, the ridge can be approximated as a metallic nanorod. With an increase of the filling factor, the ridge is widened and the aspect ratio of the nanorod is increased. Thus the resonant wavelength is red-shifted due to the increased retardation.[27] For f > 0.5, the interaction between the two adjacent corners across the air gap starts to appear and becomes dominant gradually. From the field intensity map shown in Fig.
As has been pointed out in Figs.
When the grating depth h is larger than half of the period (here h ≥ 2 μm), it can be defined as deep grating.[28] Due to the large depth, the two walls of the air gap on the grating can form a metal–insulator–metal (MIM) structure,[29] in which the wave-front and wave-end of the traveling wave can interfere and form surface plasmon standing wave (SPSW) modes.[28,30–33] The SPSW can localize energy inside the air gap and enhance the absorption and thus the emission of the grating. With an increase of f, the coupling between the two walls can be strengthened and lead to stronger emission.
To identify the order of the SPSW modes, we choose the depth of the grating to be as high as 6.0 μm in order to illustrate the antinodes and nodal points of the standing wave modes obviously. Figure 
 |

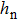

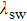

The wavelength of the SPSW resonance is closely related to the depth of the grating h and the filling factor f. As shown in Fig.
We studied the influence of the geometric parameters of the tungsten grating on its thermal emission properties. It was found that when the ratio between the depth and the period is smaller than 1/20, only SPP modes can be excited. The emission intensity is related with the filling factor. By increasing the grating depth, besides the SPP resonance, the field between adjacent corners can be coupled across the air gap of the grating when the filling factor is larger than 0.5. Further increase of the grating depth can induce surface plasmon standing wave modes because of the formation of the metal–insulator–metal structure when the filling factor is larger than 0.5. Our investigations will help understanding the mechanism of the geometric parameters affecting the emission properties of the periodic structures. Multiple resonances occurring on the tungsten grating can afford a platform to manipulate the thermal emission properties and thus offer the possibility to choose appropriate thermal emission sources according to applications. Furthermore, as the emission from the metallic grating is consistent with the absorption, our conclusions are applicable to photovoltaic and photoelectronic conversion applications.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] |










