Because of the numerous supersonic objects and the ubiquitous media in astronomical environments, there exist various shocks in the universe widely. Shocks can be generated when a jet propagates in clouds of gas and dust,^[1,2] or when a moving cloud collides with an object, for example, when the solar wind interacts with a planet such as the Earth,^[3–6] Mars,^[7,8] or Venus.^[9] Shocks are important to understand many astrophysical phenomena. It is suggested that charged particles are accelerated at the shock front,^[10,11] from which energetic cosmic rays are originated. However, it is very difficult to directly detect the astrophysical shocks by spacecraft, especially for those outside the solar system. Thus their generation mechanisms and evolution processes are not well understood, even with the help of computer simulations.^[12–14] Thanks to the development of high-power laser technology, the extreme conditions produced by intense lasers^[15,16] make it possible to simulate some astrophysical environments in the laboratory.^[17–26] With the similarity criteria,^[27,28] which could scale laboratory systems to the astrophysical ones, some laser-driven experiments have been performed to study astrophysical shocks.^[2,25,26,29] In most of those experiments, shocks are excited by using the interactions between two ablating plasmas, or between a plasma jet and a gas medium. In Ref. [30], a relatively long-lived collisionless shock is generated by the collision of a plasma plume ejected from the front surface of a planar carbon target with a spherical carbon obstacle. An observed density jump suggests the formation of a bow shock. The Mach-number of the shock is ∼2.2, which is relatively low compared to those in most astrophysical situations.

In this paper we will present the generation and evolution of a bow shock with a higher Mach-number by using a fast plasma cloud ejected from the rear of a planar CH foil colliding with a cylinder obstacle. In our experiment the bow shock is observed with shadowgraphy and interferometry. The width of the shock transition region is ×50 μm, which is similar to the ion–ion collision mean free path. Thus the shock is probably excited mainly due to ion–ion collision. The Mach-number of the ablating plasma cloud is as high as 15 at an early stage. A two-dimension hydrodynamics code, USim, is used to simulate the interaction process.

The experiments were carried out on the Shenguang II (SG II) laser facility at the National Laboratory on High Power Lasers and Physics. The experimental setup and target configuration are schematically shown in Fig. 1. Four 240 J, 1 ns, 351 nm laser beams were incident on the front surface of a mm³ CH planar foil to produce a supersonic plasma cloud at the rear side of the target. In order to simulate the astrophysical process, a plasma cloud with a large transverse width and a high longitudinal speed is necessary. This requires that the diameter of the laser focal spot should be large enough but also keep the laser intensity high. To do this, we set the spot diameter on the target surface to be , which gave an intensity of W⋅cm⁻². A polybutylene terephthalate (PBT) cylinder was placed 1 mm away from the CH target, acting as a planet-like obstacle. The axis of the cylinder was parallel to the CH target plane and at the same height as the CH target center. A 527 nm laser beam with a duration of 30 ps was used as an optical probe. The propagation direction of the probe beam was aligned in parallel with the axis of the cylinder. Shadowgraphy and Nomarski interferometry with a magnification factor ∼ 4.2 were used to measure the spatial and temporal evolution of the interaction. A time series of snapshots were obtained by changing the delay between the probe pulses and the main pulses. The delay was defined as the time separation between the falling edges of the probe and the main pluses. Soft X-ray spectra from the plasma cloud were also measured by a grazing-incidence spectrometer employing a 1200 line/mm flat-field grating with a 3° angle of incidence.

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. (color online) Schematic view of the experimental setup. Four 240 J, 1 ns, 0.351 μm laser beams were incident on the surface of a mm3 CH planar target producing a supersonic plasma cloud, which interacts with the cylinder obstacle placed 1 mm apart. The interaction was measured by shadowgraphy and Nomarski interferometry with a 527 nm, 30 ps short laser probe. The two insets show the shadowgraph and interferogram of the initial target before shooting of the main laser pulses, respectively. The blue solid circles indicate the cross section of the obstacle.

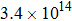
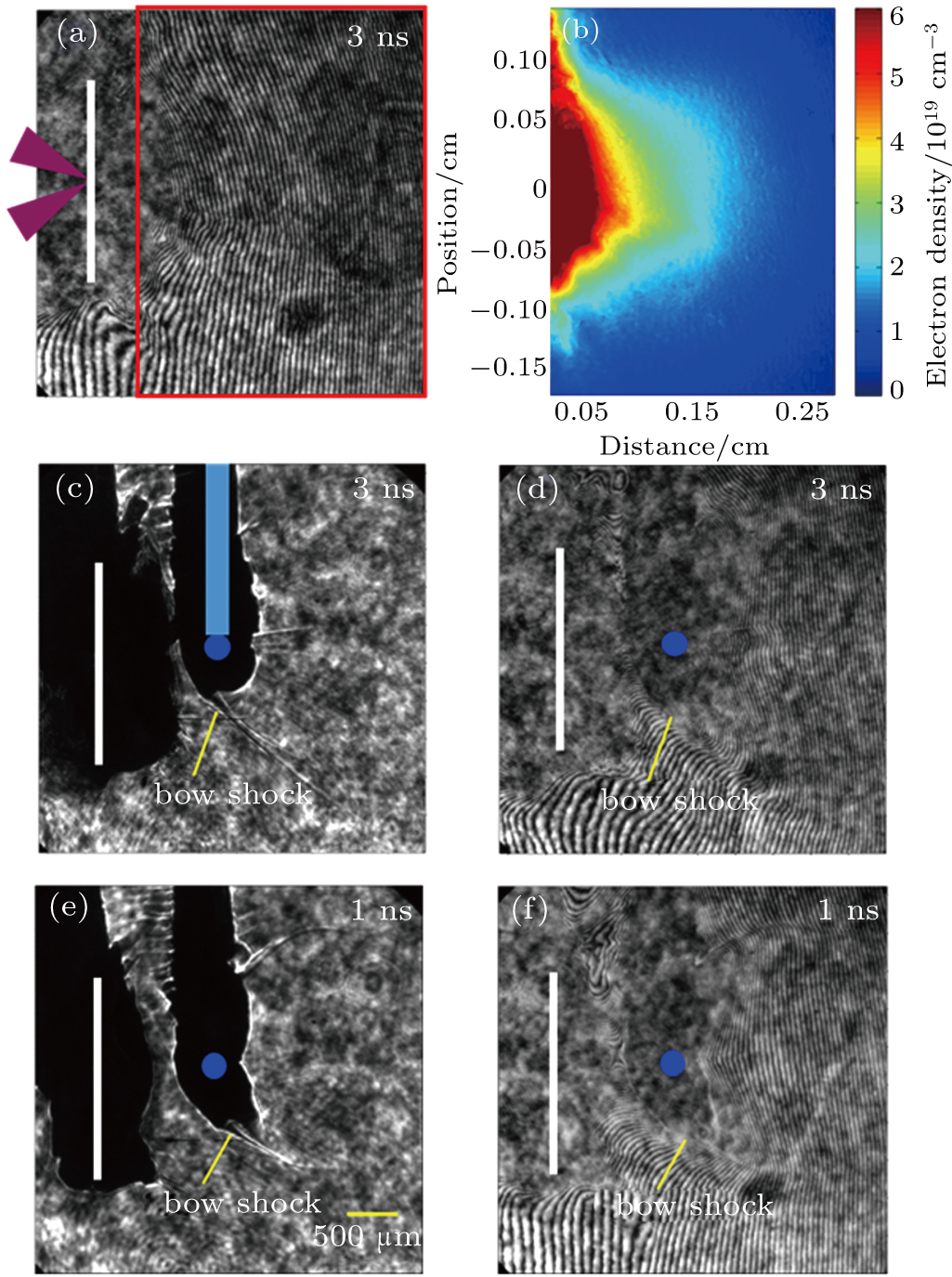
The plasma cloud behind the CH target without the obstacle was characterized firstly. Figures 2(a) and 2(b) show the measured interferogram and the electron density distribution of the cloud obtained with the Abel inversion at a delay of 3 ns, respectively. The delay is defined as the time separation between the falling edges of the probing light and the main pulse. The purple arrows represent the main laser pluses coming from the left. The position of the CH planar target is marked by the white line. After the laser irradiation, a supersonic plasma cloud moving to the right is produced from the CH target rear. From Fig. 2(b) we can see that the plasma density decreases in the target normal direction exponentially with the distance. At 3 ns, the local electron density of the plasma cloud at the position of the obstacle is ∼ 3.5 × cm⁻³, and the local average speed of the cloud there is about 300 km/s, which can be estimated by the distance and time.

Fig. 2.

Figure Option ViewDownloadNew Window

Fig. 2. (color online) (a) Interferogram of the plasma cloud without the obstacle, taken at a delay time of 3 ns. The purple arrows represent the main laser pulses. The white line indicates the original position of the CH planar target. (b) Abel inverted density map of the red box region in panel (a). (c) Shadowgraph and (d) interferogram taken at the delay time of 3 ns with the obstacle. (e) Shadowgraph and (f) interferogram taken at the delay time of 1 ns with the obstacle. The blue solid circle indicates the cross section of the obstacle.

Figures 2(c) and 2(d) show the shadowgraph and interferogram with the obstacle taken at 3 ns. The blue solid circles indicate the cross section of the obstacle. The light blue bar refers to the initial shadow of the aluminum holder hanging the obstacle. The dark regions in the shadowgraph and interferogram correspond to the high density or high density gradient regions, where the probing light is absorbed or refracted out of the collective optical system. We can see that the diameter of the cylinder obstacle plasma is expended to ∼ 500 μm, due to the ionization of the obstacle by the x-ray radiation from the CH target. Note that figures 2(c) and 2(d) are taken at the same delay time as that of Fig. 2(a). The bowlike shadow in Fig. 2(c) and the corresponding abrupt fringe discontinuities in Fig. 2(d) indicate the formation of a bow shock. We can see that the width of the shock transition is ∼ 50 μm.

Figures 2(e) and 2(f) show the bow shock taken at 1 ns. Compared with the images at 3 ns, we can see that the opening angle of the wings of the bow shock structure becomes smaller and the downstream density higher. The bow shock structure mainly depends on the Mach-number. The opening angle of the wings is determined by and the density ratio of the downstream to the upstream depends on the Mach-number as .^[31] Thus from Figs. 2(c)–2(f), we can see that the Mach-number of upstream plasma is higher at 1 ns than that at 3 ns. This is reasonable since the front part of the moving plasma cloud has larger velocity and lower temperature than the succeeding part.

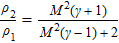
The soft x-ray spectrum in the wavelength range 20–50 Å was measured with a grazing-incidence spectrometer. Figure 3(a) shows a typical spectrum. The characteristic emission lines He-like and H-like carbon ions dominate the spectrum. Using a collisional–radiative (CR) model,^[20,32] the electron temperature at the obstacle region is fitted to be about 90 eV, as shown in Fig. 3(b). With the temperature, the local thermal pressure and sound speed of the cloud are estimated to be 3.15 ∼ Pa and 80 km/s, respectively.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (color online) (a) The characteristic spectral lines obtained by the grazing-incidence spectrometer. (b) Comparison between experimental result and simulated results from 30 Å to 44 Å.

We have used the USim, a two-dimension hydrodynamics code based on Euler equations, to simulate the interaction of the plasma cloud with the obstacle. The cylinder obstacle is set as a circle solid disk immersed in the cloud flow in the simulations. The diameter of the circle disk is set as 500 μm, which is the same as the size of the ionized obstacle measured in the experiment. The plasma cloud moves in from the left boundary of the simulation space. The boundary conditions of the space are absorptive. The cloud is reflected when interacting with the circle disk. We also used the same initial values of the thermal pressure and density of the cloud as the experiment. The whole process is assumed to be adiabatic, that is, the polytropic index .

Figure 4(a) shows the simulated shock wave at 3 ns when using the local velocity of the cloud at the obstacle, 300 km/s, obtained from the interferogram in Fig. 2(a). We can see that the shock structure can well reproduce the experimental one in Fig. 2(c). This also indicates that one can deduce the velocity of the incident plasma cloud by matching the experimental shock structure with the simulated one. In this way, by fitting the shock structure in Fig. 2(e), the local velocity of the cloud at 1 ns is estimated to be 1200 km/s, which corresponds to a Mach-number as high as 15.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (color online) Simulated bow shock structures by the USim at (a) 3 ns and (b) 1 ns, respectively.

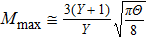
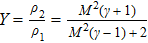
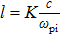
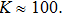
Previous work demonstrates a collisionless shock in the interaction of a plasma plume with an obstacle.^[30] Collisionless shocks are typically mediated by electrostatic or electromagnetic instabilities. For the electrostatic case, the maximum Mach number is determined by , where Y and Θ are the ratio of electron densities and electron temperatures between the downstream and upstream, respectively.^[33] In our experiment, the density ratio of downstream and upstream is about 3.3 at 3 ns and 3.9 at 1 ns, which gives . The initial electron temperature of the plasma from the cylinder obstacle is much lower than that of the CH plasma cloud. Therefore, Θ is lower than 1 in our case. Here we take to calculate the upper limit of the maximum Mach number of the shock, , which is 2.5. One can see that the calculated upper limit of is lower than the measured ones: 3.75 at 3 ns and 15 at 1 ns. This indicates that the electrostatic instability is not important in our experiment. For the electromagnetic case, the width of the shock transition is , where K is a number factor, c is the speed of light, and is ion plasma frequency.^[34] Based on numerical simulations,^[13] Thus, l is about 6 mm in our experiment, which is much higher than the measured one.

To figure out that the shock we observed is collision-dominated or collisionless-dominated, we have calculated the ion–ion collision mean free path 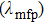. In our case, the incident plasma cloud from the rear target surface interacts with the ionized plasma from the obstacle. The mean free path characterizing their interactions at 3 ns can be expressed as^[35] , where A, Z, and are the atomic weight, average ionization state, and number density of the main ion component (carbon ions), v is the relative flow velocity between the two colliding plasmas, which is taken to be ∼ 300 km/s according to the experimental and simulated results. For carbon ions, A = 12. From the spectrum in Fig. 3, the ionization state is taken as 5 for the electron temperature of 90 eV. From Figs. 2(c) and 2(d), one can see that the electron density of the ionized plasma of the obstacle is too high, which leads to the blackout shadow regions. Therefore, we use the electron density of the incident CH plasma cloud at the front of the bow shock to estimate the lower limit of . That is cm⁻³, obtained with the local electron density at the corresponding region of the obstacle from Fig. 2(a). This gives us the upper limit of . Note that the actual value of at the blackout region is far less than 130 μm. This indicates that may be comparable to the experimentally measured width of the shock transition (∼ 50 μm). Taking the above discussion on the collisionless and the comparison of with the width of the shock transition, we believe that the ion–ion collision would be more important for the shock formation than the collisionless under our experimental conditions.

A bow shock is demonstrated in the interaction of a high Mach-number, laser-driven plasma cloud with a cylinder obstacle on the SG II laser facility. The width of the shock transition region observed by the shadowgraphy and interferometry is ∼ 50 μm, which is comparable to the ion–ion collision mean free path. This indicates that the shock is mainly collisional probably. The Mach-number of the shock is measured to be ∼ 15 at an early stage, and decreases with time. This leads to the change of the bow shock shape. Our results indicate the possibility of investigating shocks relevant to astrophysics through similarity criteria in the laboratory.