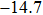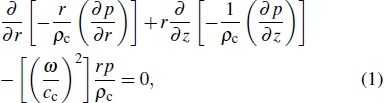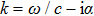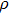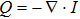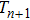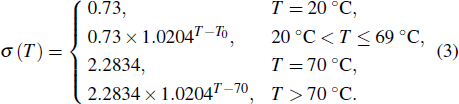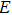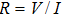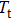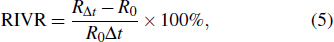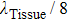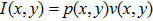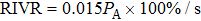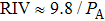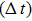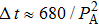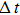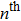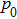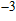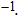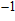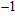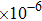Noninvasive treatment efficacy monitoring and dose control for high-intensity focused ultrasound therapy using relative electrical impedance variation
1. IntroductionHigh-intensity focused ultrasound (HIFU)[1–6] can converge sound wave to the focal area, raise temperature and destroy tumour cells by thermocoagulation necrosis in a short time. HIFU therapy, which has the advantages[7] of non-invasiveness, little trauma, rapid recovery and less metastasis, is considered as one of the most promising technologies for tumour treatment in the 21
 century. It is extremely important to ensure the reliability and safety of thermocoagulation and cause as little damage to surrounding tissues as possible. Consequently, the real-time temperature monitoring or efficacy evaluation has a great significance for the application of HIFU therapy.
century. It is extremely important to ensure the reliability and safety of thermocoagulation and cause as little damage to surrounding tissues as possible. Consequently, the real-time temperature monitoring or efficacy evaluation has a great significance for the application of HIFU therapy.
Although the temperature inside the body can be predicted based on the heat radiation from body surface, the application of infrared temperature measurement technology is still limited by short penetration depth and poor measurement accuracy. Temperature image can be reconstructed by magnetic resonance imaging[8–10] (MRI), which is based on the measurements of temperature-dependent diffusion coefficient, proton resonance frequency, or relaxation time without ionizing radiation. However, the application of MRI is limited because of its poor temporal resolution and high cost. During the past decades, several ultrasonic measurement technologies[11–13] have been proposed to be integrated into HIFU system. Based on the measurements of echo time shift and nonlinear distortion, temperature estimation has been performed using variations of acoustic velocity, impedance and nonlinear parameters. Since temperature dependent variations of these acoustic parameters were relatively small, the accuracy of temperature measurements was unsatisfactory for biomedical applications. In addition, even though ultrasound imaging[14] can be used to guide HIFU location and monitor blood flow, and quantitative ultrasound imaging[15] has a potential for use in non-invasive monitoring of HIFU exposure, it is still insufficient for the precise temperature measurement and efficacy evaluation during HIFU treatment.
It was reported that the electrical conductivity of normal tissues was 0–0.5 S/m[16] at the frequency less than 1 MHz, which was temperature dependent. Griffiths[17] found a nearly linear relationship between the impedance and temperature changes of agar with the temperature-impedance variation factor (TIVF) of about
 %/°C. Zurbuchen[18] reported that the conductivity of pork liver increased with temperature. The conductivities at 37 °C and 70 °C were 0.41 and 0.79 S/m, respectively, with the variation of almost 100%. Dong[19] discovered that TIVF of rabbit liver was
%/°C. Zurbuchen[18] reported that the conductivity of pork liver increased with temperature. The conductivities at 37 °C and 70 °C were 0.41 and 0.79 S/m, respectively, with the variation of almost 100%. Dong[19] discovered that TIVF of rabbit liver was
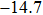 %/°C at 70 °C during irreversible tissue thermocoagulation. Compared with acoustic impedance, greater TIVF could be used to design more sensitive temperature measurement modality. In HIFU therapy, wide impedance variation in the focal region provided solid physical basis for precise temperature monitoring, and significant impedance variation of thermocoagulation also provided a high-contrast indicator for efficacy evaluation. However, the application of electrical impedance tomography (EIT)[20–22] was still limited by the poor spatial resolution of the gradient temperature distribution in millimetre-scale focal region using limited number of electrodes.
%/°C at 70 °C during irreversible tissue thermocoagulation. Compared with acoustic impedance, greater TIVF could be used to design more sensitive temperature measurement modality. In HIFU therapy, wide impedance variation in the focal region provided solid physical basis for precise temperature monitoring, and significant impedance variation of thermocoagulation also provided a high-contrast indicator for efficacy evaluation. However, the application of electrical impedance tomography (EIT)[20–22] was still limited by the poor spatial resolution of the gradient temperature distribution in millimetre-scale focal region using limited number of electrodes.
In this study, a double-electrode measurement model was established to investigate the relationship among electrical impedance, acoustic power, and treatment time during HIFU therapy, and a method of critical temperature (70 °C) monitoring and efficacy evaluation for thermocoagulation was proposed as well. Based on the temperature–impedance relationship, a 3-D model was established using the finite element method (FEM) to simulate the distributions of acoustic pressure, temperature, and conductivity of a cylinder phantom. Subsequently, the relative electrical impedance variation (RIV) was calculated with simulated distributions of electrical potential and current density. According to the experimental setup, real-time impedances of a cylindrical tissue-mimicking phantom were measured at different acoustic powers and treatment times, and RIVs were calculated and compared with theoretical results. Once HIFU treatment efficacy was achieved with the temperature of focal region (within
 mm in radial directions) reaching 70 °C, the relationship between RIV, acoustic power, and treatment time was analysed quantitatively. It was established that the required RIV and treatment time are inversely proportional to the acoustic power and to the square of acoustic power, respectively. These results suggest that RIV can be used as a sensitive indicator for non-invasive temperature monitoring and efficacy evaluation, and that it may provide a new strategy for accurate dose control in HIFU therapy.
mm in radial directions) reaching 70 °C, the relationship between RIV, acoustic power, and treatment time was analysed quantitatively. It was established that the required RIV and treatment time are inversely proportional to the acoustic power and to the square of acoustic power, respectively. These results suggest that RIV can be used as a sensitive indicator for non-invasive temperature monitoring and efficacy evaluation, and that it may provide a new strategy for accurate dose control in HIFU therapy.
2. Principle and methodThe schematic diagram of HIFU therapy and electrical impedance measurement system is illustrated in Fig. 1. Since the spherical HIFU transducer is axisymmetric, the acoustic pressure can be described with the homogeneous Helmholtz equation in 2D cylindrical coordinates as follows:[23,24]
where
r and
z are the radial and axial coordinates,
p is the acoustic pressure,
ω is the angular frequency, density

and acoustic speed
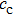
are complex-valued to account for the damping properties of the media. Using attenuation coefficient
α, the wave number in viscous media can be described as
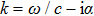
,
[24] and then the corresponding density and sound speed can be calculated as
 [24]
[24] and

,
[24] where
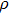
and
c are the density and sound speed in the media without attenuation.
In HIFU therapy, the energy deposition[25] (heat source) can be calculated using
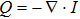 , where
, where
 represents the time average of the product between acoustic pressure and particle vibration velocity. Then, the heat source expression can be reduced to
represents the time average of the product between acoustic pressure and particle vibration velocity. Then, the heat source expression can be reduced to
 , where
, where
 and
and
 are the density and acoustic speed of tissues, respectively. To predict temperature rise accurately, simplified Pennes bio-heat transfer equation[26] is used to avoid the impact of blood perfusion
are the density and acoustic speed of tissues, respectively. To predict temperature rise accurately, simplified Pennes bio-heat transfer equation[26] is used to avoid the impact of blood perfusion
where

and

are the specific heat and thermal conductivities of tissues,
T is the increased temperature, and

is the initial temperature of 20 °C.
To analyse impedance variation quantitatively, the commonly used temperature-impedance variation factor (
 [19] is applied, where
[19] is applied, where
 and
and
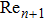 are resistive components of the electrical impedances at
are resistive components of the electrical impedances at
 (°C) and
(°C) and
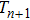 (°C). Experimental results prove that TIVF of the egg white gel used in this study fluctuated substantially at −2%/°C for
(°C). Experimental results prove that TIVF of the egg white gel used in this study fluctuated substantially at −2%/°C for
 C. When irreversible thermocoagulation occurred at 70 °C, TIVF jumped to
C. When irreversible thermocoagulation occurred at 70 °C, TIVF jumped to
 %/°C. Then, TIVF restored to about −2%/°C for
%/°C. Then, TIVF restored to about −2%/°C for
 C. Thus, the temperature-conductivity relation can be described as
C. Thus, the temperature-conductivity relation can be described as
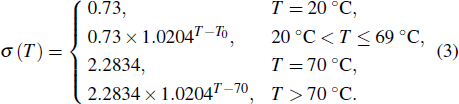 | |
By applying the temperature-conductivity relation in Eq. (3) to the acoustic and temperature fields, the conductivity distributions in the focal region can be calculated during HIFU therapy. Assuming that two electrodes with constant current (
 ) injection are fixed on the surface of the phantom model, the electrical potential and current density inside the model can be simulated using the electrical equations
) injection are fixed on the surface of the phantom model, the electrical potential and current density inside the model can be simulated using the electrical equations
 ,
,
 , and
, and
 , where Q is the current source,
, where Q is the current source,
 is the current density, V is the electric potential, and
is the current density, V is the electric potential, and
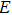 is the electrical intensity. Then, the electrical impedance of the model can be calculated from the formula
is the electrical intensity. Then, the electrical impedance of the model can be calculated from the formula
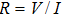 (with the electrical potential difference V between the electrodes), which contains the information about the electrical impedance distribution in the focal region.
(with the electrical potential difference V between the electrodes), which contains the information about the electrical impedance distribution in the focal region.
In traditional hyperthermia, thermal dose (TD) was often used to quantitatively evaluate the degree of thermal damage. Sapareto[27] and Meaney[28] pointed out that TD is related to heating time and temperature variation as
 , where
, where
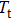 is time-dependent temperature,
is time-dependent temperature,
 and
and
 represented the initial and end time of thermal therapy. TD obtained at 43 °C during 120 min is approximately equal to that obtained at 56 °C during 1 s, which was considered as the least TD of thermal lesion. However, for the high-speed treatment of HIFU therapy in a very small focal region, in which case heat conduction and diffusion are unavoidable, it is difficult to estimate temperature and TD accurately. Consequently, an improved method of efficacy monitoring and dose control applicable to HIFU therapy should be developed.
represented the initial and end time of thermal therapy. TD obtained at 43 °C during 120 min is approximately equal to that obtained at 56 °C during 1 s, which was considered as the least TD of thermal lesion. However, for the high-speed treatment of HIFU therapy in a very small focal region, in which case heat conduction and diffusion are unavoidable, it is difficult to estimate temperature and TD accurately. Consequently, an improved method of efficacy monitoring and dose control applicable to HIFU therapy should be developed.
Based on the temperature–conductivity relation, the wide range of conductivity variation can be used for sensitive monitoring of temperature rise and treatment efficacy in tissues. Whereas, since the base electrical impedances of the phantoms having different shapes and sizes are different, the accurate information of conductivity variation or temperature rise in the focal region cannot be achieved with measurements of absolute electrical impedances alone. In order to avoid the influence of absolute impedance of phantom, two parameters of relative electrical impedance variation (RIV) and relative electrical impedance variation rate (RIVR) are defined as
where

is treatment duration,
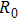
and

are resistive components of the electrical impedances of the phantom before and after therapy, respectively. Meanwhile, when the temperature of the focal region (in radial

mm) reaches 70 °C, irreversible thermocoagulation of tissues takes place and HIFU treatment efficacy is realized. Therefore, the value of RIV of the phantom under this condition can be used as the indicator for critical temperature monitoring and efficacy evaluation, and the corresponding required RIV and treatment time can also be applied for accurate dose control in HIFU therapy.
3. Numerical studyAs shown in Fig. 1, numerical studies were conducted for a cylindrical tissue phantom model to simulate the processes of HIFU therapy, pressure distribution, temperature rise, conductivity variation and electrical impedance measurement with the modules of acoustics, bio-heat transfer and electrical field using the finite element method (FEM, COMSOL Multiphysics 5.2a, COMSOL Inc., Sweden). Since the acoustic and electrical modules were only coupled by the relationship between temperature and electrical impedance of tissues, the calculations could be separated completely in simulations. The entire process included the following five steps. First, distributions of acoustic pressure and intensity in the focal region were simulated for different source pressures (displacements or velocities) based on the acoustic wave equation (Eq. (1)). Second, based on the thermal effect of ultrasound, the distributions of acoustic intensity were employed as inputs of bio-heat transfer for heat source
 to simulate temperature distributions using Eq. (2). Third, by employing the piecewise temperature-conductivity function in Eq. (3) to the simulated temperature distributions, the conductivity distributions in the focal region were calculated. Fourth, in electrical module, through constant current injection from two electrodes fixed on the surface of the phantom model, the distributions of current density and electrical potential were simulated for the focal regions with corresponding conductivity distributions. Fifth, real-time data for the electrical impedance of the phantom model and the corresponding RIVs were obtained from the electrical potential difference between the two electrodes, reflecting the information on the temperature distribution and treatment efficacy in the focal region during HIFU therapy.
to simulate temperature distributions using Eq. (2). Third, by employing the piecewise temperature-conductivity function in Eq. (3) to the simulated temperature distributions, the conductivity distributions in the focal region were calculated. Fourth, in electrical module, through constant current injection from two electrodes fixed on the surface of the phantom model, the distributions of current density and electrical potential were simulated for the focal regions with corresponding conductivity distributions. Fifth, real-time data for the electrical impedance of the phantom model and the corresponding RIVs were obtained from the electrical potential difference between the two electrodes, reflecting the information on the temperature distribution and treatment efficacy in the focal region during HIFU therapy.
In order to speed up the simulation with appropriate accuracy, the mesh sizes in water and tissue phantom were set to
 and
and
 , and the mesh size at the focal region was set to
, and the mesh size at the focal region was set to
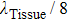 . The parameters of the experimental transducer (diameter 10 cm, focal length 10 cm, centre frequency 1.13 MHz) were used in simulations. A tissue-mimicking egg white gel phantom[29] prepared in a cylindrical transparent acrylic mould (diameter 3.2 cm, height 3.5 cm) was placed in the focal region to conduct HIFU therapy. Two strip electrodes (3.5 cm × 2.5 cm) were arranged at both sides of the phantom, with one end connected to the ground and the other to a constant current source to measure the electrical impedance at the frequency from 10 kHz to 1 MHz, which was less than the frequency of therapeutic ultrasound to reduce mutual interference. The averaged resistive parts of the measured electrical impedances were calculated and used as the results of the phantom model. In addition, the parameters of the phantom used in simulations are listed in Table 1.
. The parameters of the experimental transducer (diameter 10 cm, focal length 10 cm, centre frequency 1.13 MHz) were used in simulations. A tissue-mimicking egg white gel phantom[29] prepared in a cylindrical transparent acrylic mould (diameter 3.2 cm, height 3.5 cm) was placed in the focal region to conduct HIFU therapy. Two strip electrodes (3.5 cm × 2.5 cm) were arranged at both sides of the phantom, with one end connected to the ground and the other to a constant current source to measure the electrical impedance at the frequency from 10 kHz to 1 MHz, which was less than the frequency of therapeutic ultrasound to reduce mutual interference. The averaged resistive parts of the measured electrical impedances were calculated and used as the results of the phantom model. In addition, the parameters of the phantom used in simulations are listed in Table 1.
Table 1.
Table 1.
 | Table 1.
Parameters used in simulations at the temperature of 293 K (20 °C).
. |
In order to realize accurate power calibration for simulations in FEM, the experimental displacements of 6.2, 6.7, 7.7, 9.2 and 10.2 nm on the transducer surface were measured with a laser vibrometer (Polytec, OFV-503 and OFV-2570, Polytec Ltd, German) at the output signal amplitudes of 300, 350, 375, 400 and 450 mV. In FEM simulations, the five measured displacements were used as the parameters to calculate the distributions of acoustic pressure and intensity in the focal region. The effective cross-sectional area
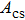 in the centre region of the focal plane was defined for all the points with the acoustic pressure higher than 50% (
in the centre region of the focal plane was defined for all the points with the acoustic pressure higher than 50% (
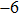 dB criterion) of the maximum pressure at the focal point. Accordingly, the acoustic power was calculated as a surface integral
dB criterion) of the maximum pressure at the focal point. Accordingly, the acoustic power was calculated as a surface integral
 for the acoustic intensity
for the acoustic intensity
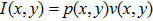 . Depending on excitation conditions, the acoustic power values of 5.79, 6.76, 8.93, 12.75, and 15.68 W were obtained and used for calibration in further numerical and experimental studies.
. Depending on excitation conditions, the acoustic power values of 5.79, 6.76, 8.93, 12.75, and 15.68 W were obtained and used for calibration in further numerical and experimental studies.
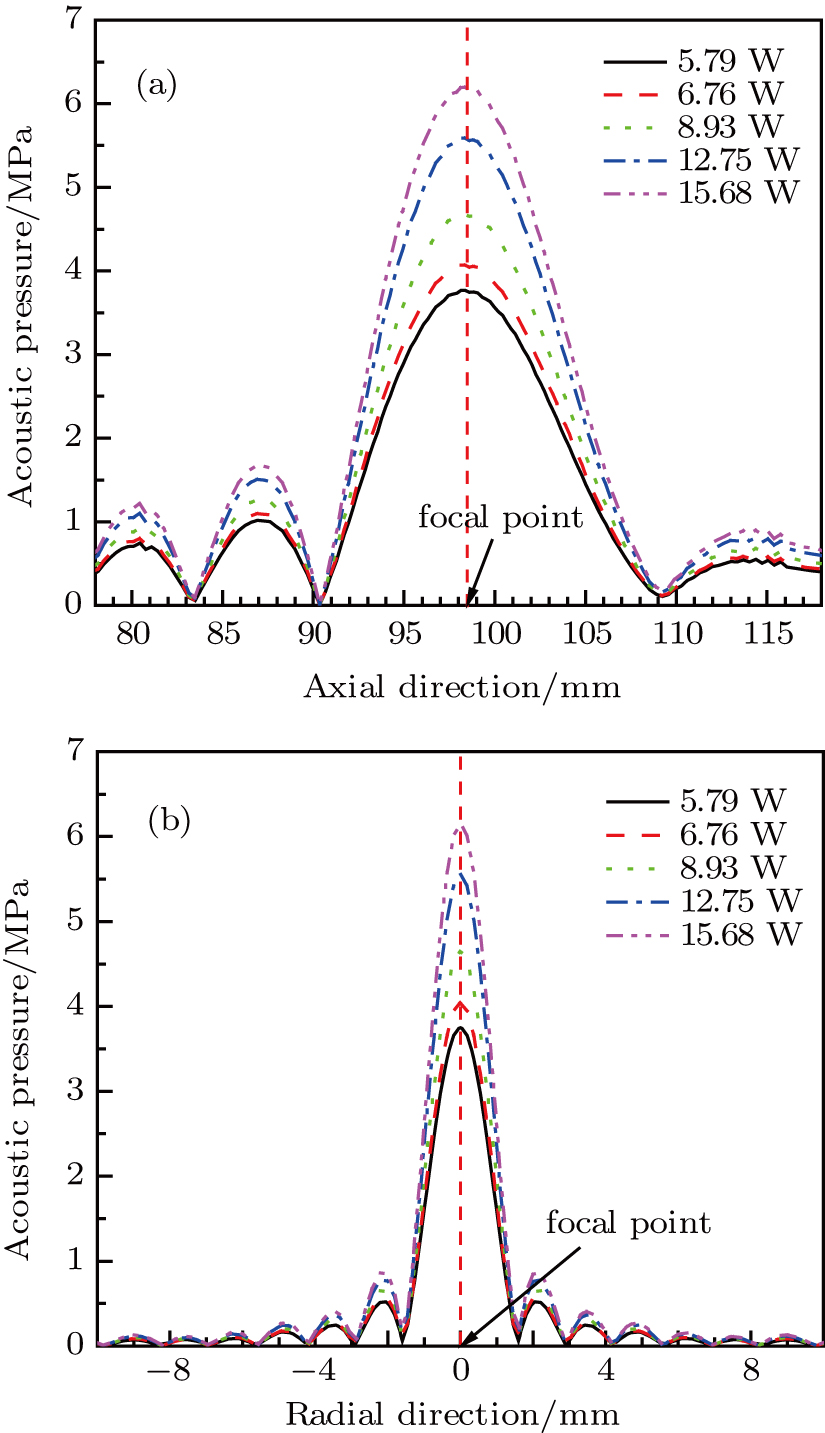
Based on Eq. (1), the axial and radial distributions of acoustic pressure in the focal region at different acoustic powers were simulated. As illustrated in Figs. 2(a) and 2(b), the axial and radial distributions of acoustic pressure are essentially the same for different magnitudes of acoustic power, except for amplitude differences. An approximate ellipsoidal focal region with the highest pressure at the focal point (z = 98.6 mm) can be generated. The acoustic energy is concentrated in the centre region with a radius less than 1 mm. When the acoustic power is raised from 5.79 to 15.68 W, the maximum acoustic pressure increases from 3.7 to 6.1 MPa at the focal point.
Using Eq. (2), 2D axial profiles of temperature at different treatment times with the acoustic power of 15.68 W were simulated, as plotted in Fig. 3(a). Due to the effects of thermal diffusion, expanded focal region with higher temperature is observed at longer treatment time. For treatment times less than 1.5 s, the highest temperature is lower than 70 °C. When treatment time reaches 2.5 s, HIFU treatment efficacy realizes with the centre temperature higher than 70 °C. Increasing treatment time further to 3.0 s leads to continuous increases in the temperature at the focal centre to 86 °C, accompanied by an expansion of the thermocoagulation area. By applying the temperature-conductivity relation to the data plotted in Fig. 3(a), the corresponding distributions of electrical conductivity were obtained, as presented in Fig. 3(b). Low conductivity (
 S/m) is displayed (in blue) for the low temperature (
S/m) is displayed (in blue) for the low temperature (
 °C) when treatment time is less than 1.5 s. When treatment time reaches 2.5 s, thermocoagulation takes place in the focal region with the critical conductivity (2.28 S/m) (in orange). For further increases in treatment time, higher conductivity is obtained (displayed in red) with expanded boundary of critical conductivity (in orange).
°C) when treatment time is less than 1.5 s. When treatment time reaches 2.5 s, thermocoagulation takes place in the focal region with the critical conductivity (2.28 S/m) (in orange). For further increases in treatment time, higher conductivity is obtained (displayed in red) with expanded boundary of critical conductivity (in orange).
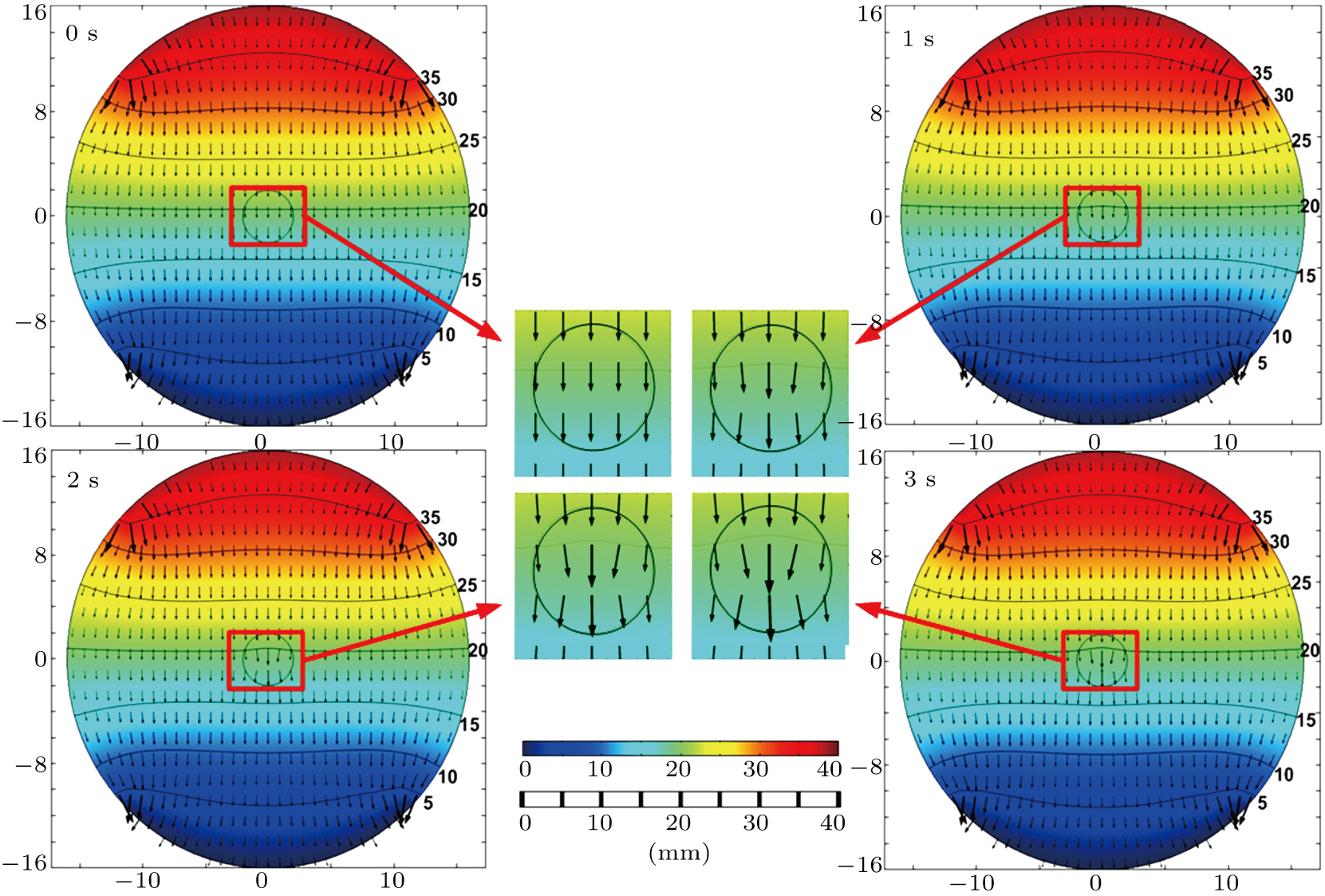
During HIFU therapy, the distribution of electrical field between the two electrodes is impacted by the enhanced electrical conductivity in the focal region, resulting in reduced electrical impedance of the phantom model. By applying the conductivity distributions to the electrical field with constant current injection from the two electrodes, the distributions of electrical potential and current density were simulated in FEM based on the conductivity distributions plotted in Fig. 3(b). The cross-sectional distributions in the focal plane at different treatment times are plotted in Fig. 4 with the locally enlarged focal regions for comparison. The vertical and horizontal distributions of electrical potential and current density are uniform at the treatment time of 0. Before HIFU therapy, the distributions of current density in the centre region are uniform with current directions pointing downward. With the increase in treatment time, the ambient currents converge to the focal centre for the enhanced conductivity, producing curved equipotential lines and reduced electrical impedance of the phantom model.
Treatment times that are required to reach full HIFU treatment efficacy were calculated to be 21.4, 13.8, 7.0, 3.4, and 2.4 s at acoustic powers of 5.79, 6.76, 8.93, 12.75, and 15.68 W, respectively. The 2D axial profiles of temperature are illustrated in Figs. 5(a) with the corresponding 1D axial temperature distributions plotted in Fig. 5(b) for precise analyses. It can be observed that, in spite of the same size of thermocoagulation area, larger thermal diffusion area is generated by longer treatment time at lower acoustic power. When acoustic power increases from 5.79 to 15.68 W, the temperature at the focal point increases from 74.3 °C to 78.8 °C, while the axial width of the isothermal level of 70 °C keeps a constant value of 3.8 mm and the axial width of the isothermal level of 45 °C (low temperature therapy) decreases from 11.6 to 9.7 mm. Therefore, reduced impact of thermal diffusion on surrounding tissues can be achieved at higher acoustic power with shorter treatment time, which is beneficial for the realization of fast and accurate HIFU therapy.
Using the temperature-conductivity relation, 2D axial profiles of electrical conductivity were calculated from the data presented in Fig. 5(a) and plotted in Fig. 6. Once HIFU treatment efficacy is reached, the thermocoagulation area (orange to red, temperature is higher than 70 °C, conductivity is higher than 2.28 S/m) remains essentially the same with a wider surrounding transition region (green to yellow), although the focal region under lower acoustic power is enlarged. Meanwhile, reduced impact of thermal diffusion on surrounding tissues can be achieved using shorter treatment time and higher acoustic power, demonstrating the feasibility of precise size control in HIFU therapy.
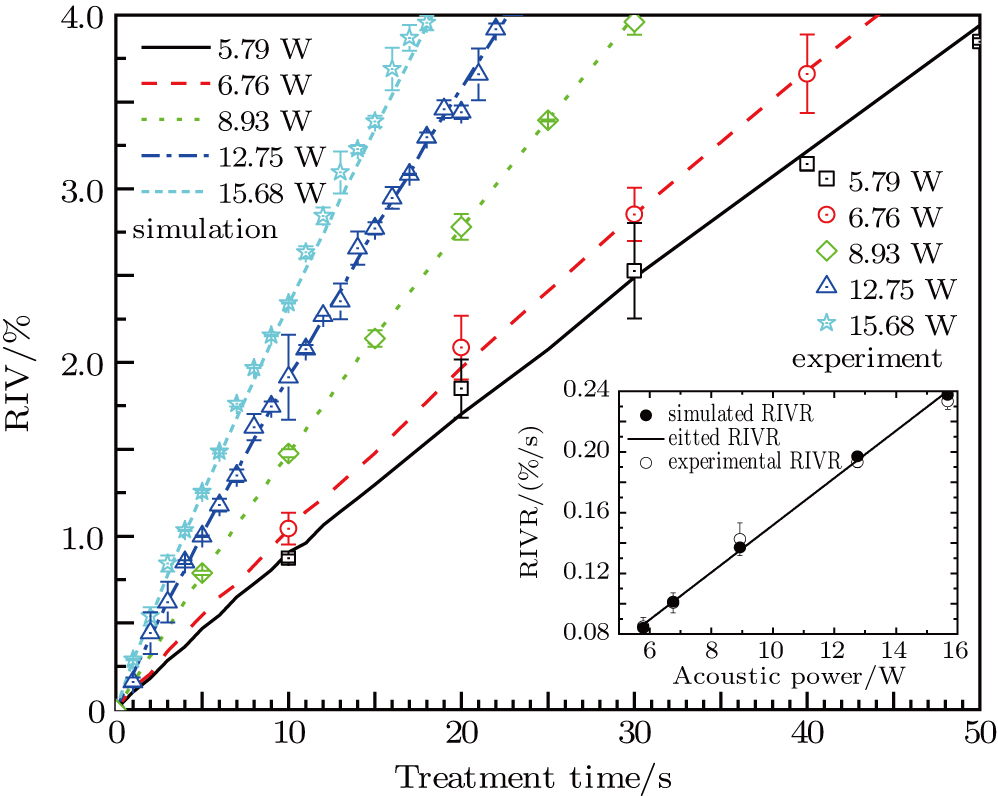
The dependences of RIV on treatment time for different values of acoustic power were calculated based on electrical impedance simulations for the phantom (lines in Fig. 7). It is clear that RIV increases linearly with treatment time at a fixed acoustic power. Faster increase of RIV (larger positive slope) can be produced by higher acoustic power. By calculating the slope for each acoustic power, RIVRs at different acoustic powers were obtained (the inset in Fig. 7). The linear acoustic power dependence of RIVR can be fitted to
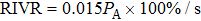 , where
, where
 denotes the value of acoustic power. Therefore, the acoustic power of the transducer can be estimated from RIVR calculation based on RIV measurements at different treatment times.
denotes the value of acoustic power. Therefore, the acoustic power of the transducer can be estimated from RIVR calculation based on RIV measurements at different treatment times.
The dependence of RIV required for reaching HIFU treatment efficacy on acoustic power shows that larger RIV can be generated by expanded focal region using longer treatment time at lower acoustic power (Fig. 8). For example, an increase in RIV from 0.59% to 1.8% is produced by a decrease in acoustic power from 15.68 W to 5.79 W. The inverse relationship between RIV and acoustic power can be fit by a formula
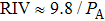 . Moreover, from the acoustic power dependence of treatment time, which is plotted in Fig. 8, it follows that shorter treatment time is required for higher acoustic power to realize HIFU treatment efficacy. By considering the physical mechanism of thermal diffusion, the required treatment time
. Moreover, from the acoustic power dependence of treatment time, which is plotted in Fig. 8, it follows that shorter treatment time is required for higher acoustic power to realize HIFU treatment efficacy. By considering the physical mechanism of thermal diffusion, the required treatment time
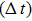 with respect to acoustic power can be approximated as
with respect to acoustic power can be approximated as
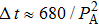 , indicating that
, indicating that
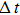 is inversely proportional to the square of acoustic power and can be estimated from acoustic power in HIFU therapy.
is inversely proportional to the square of acoustic power and can be estimated from acoustic power in HIFU therapy.
4. Experimental studyThe experimental schematic diagram of HIFU therapy and impedance measurement is illustrated in Fig. 1. A sinusoidal wave (1.13 MHz) was sent out by the functional waveform generator (Agilent 33250A, Agilent Technologies, USA). After being amplified by the power amplifier (53 dB, 2200L, Electronics and Innovation Ltd, USA), the signal was used to drive the transducer to excite focused sound beam into the phantom. Two strip copper electrodes (3.5 cm × 2.5 cm × 0.1 cm) symmetrically positioned on the phantom model were connected to the electrical impedance analyser (Agilent 4294A, Agilent Technologies, USA) to conduct real-time electrical impedance measurements.
A transparent tissue-mimicking egg white gel phantom[29] was prepared by sol-gel method: 10 g of acrylamide, 0.05 g of ammonium persulfate, 0.3 g of bis-acrylamide and 35 ml of egg white were mixed together and put into 0.9% physiological saline to make 100 ml sol-gel. Then, 0.2 ml of tetramethylethylenediamine was added, the mixture was stirred evenly and poured into the cylindrical acrylic mould for solidification. The physical parameters of the phantom were similar to those of biological tissues. In particular, upon reaching HIFU treatment efficacy, the transparent gel turned into opaque white, which could be used for sensitive indication of thermocoagulation.
In our experiments, HIFU therapy and electrical impedance measurements were conducted on a cylindrical egg white gel phantom by adjusting the amplitudes of output signals at the acoustic power values of 5.79, 6.76, 8.93, 12.75, and 15.68 W. For each acoustic power, the electrical impedances were measured at a fixed time interval, and the experiments were repeated 5 times to obtain data average. The averaged resistive components of the electrical impedances measured at different times at frequencies from 10 kHz to 1 MHz were obtained for RIV calculation. The experimental RIVs for different treatment times and acoustic power values (scattered points in Fig. 7) are consistent with the corresponding simulation results with a maximum relative error of about 2.9%. It can be observed experimentally by increasing the treatment time that a white ellipsoidal thermocoagulation focal region appears with a gradually increasing size and decreasing electrical impedance, resulting in an enhanced RIV. For higher acoustic power, thermocoagulation can be generated in a shorter time with a rapid increase of RIV.
Based on linear interpolation for the experimental results in Fig. 7 obtained for the acoustic power values of 5.79, 6.76, 8.93, 12.75, and 15.68 W, RIVs of 1.82%, 1.39%, 1.01%, 0.66%, and 0.56% were calculated for respective treatment times (viz., 21.4, 13.8, 7.0, 3.4, and 2.4 s) required to reach HIFU treatment efficacy, as plotted in Fig. 8. The consistency of the results further confirms that the required RIV and treatment time are inversely proportional to the acoustic power and square of acoustic power, respectively. In addition, it was also proved experimentally that the HIFU treatment efficacy of thermocoagulation could never be realized at acoustic power less than 4 W due to the influence of thermal diffusion. Therefore, this low power regime should not be used in practical applications of HIFU therapy.
5. DiscussionIn previous studies of HIFU propagation, the acoustic field was often considered to be nonlinear,[30,31] and the absorption coefficient[32] was dependent on working frequency. The higher frequency field components are absorbed stronger, resulting in additional temperature rise. Meanwhile, it was also demonstrated that the nonlinear acoustothermal effect of HIFU was determined by the configuration and acoustic pressure of the focused transducer. Crum et al.[33] reported that, although the difference between linear and nonlinear estimates of heat rate was substantial for a given HIFU procedure, the difference in temperature prediction was much smaller because of thermal conduction. Based on the investigation of nonlinear effects for focused ultrasound beam, Myers and Soneson[34–36] showed that
 temperature harmonic is less important (relative to the fundamental) than
temperature harmonic is less important (relative to the fundamental) than
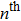 heat-source harmonic by a factor of
heat-source harmonic by a factor of
 . In their study of thresholds for nonlinear effects in HIFU propagation and tissue heating, the threshold for nonlinear effects was proved to be about 115 W[34–36] for 10% error of temperature rise. The nonlinearity parameter
. In their study of thresholds for nonlinear effects in HIFU propagation and tissue heating, the threshold for nonlinear effects was proved to be about 115 W[34–36] for 10% error of temperature rise. The nonlinearity parameter
 and the linear pressure gain
and the linear pressure gain
 [34–36] were proposed to analyse the relative difference in focal temperature rise between linear and nonlinear effects, where a, d, and f are the radius, focal length and frequency of the transducer,
[34–36] were proposed to analyse the relative difference in focal temperature rise between linear and nonlinear effects, where a, d, and f are the radius, focal length and frequency of the transducer,
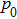 is the peak pressure on transducer face and β is the nonlinear coefficient of the phantom. For the transducer parameters used in our study, we obtained G = 56.6 and N = 0.0953 for nonlinear coefficient β = 4.5 and absorption coefficient α = 0.74 at the acoustic power of 15.68 W. It can be observed from Fig. 5[34] that the error between linear and nonlinear components in focal temperature rise is much smaller than 2% for G = 56.6 and N = 0.0953. Therefore, a linear model should be sufficient for temperature predictions[34] in the present study, although a nonlinear model might provide more accurate predictions for heat generation and temperature rise. However, for acoustic power higher than 115 W, the nonlinear effects in HIFU propagation and tissue heating are inevitable, and the acoustothermal effects of intensive cavitation[37–41] cannot be ignored. In order to analyse the temperature characteristics of HIFU therapy accurately, nonlinear Khokhlov–Zabolotskaya–Kuznetsov equation (KZK)[42,43] or spheroidal beam equation (SBE)[44,45] should be applied in future studies. In addition, to take into account blood flow and tissue inhomogeneity, more realistic models[46] with the properties closer to living tissues should be developed to obtain more accurate efficacy monitoring and dose control in HIFU therapy.
is the peak pressure on transducer face and β is the nonlinear coefficient of the phantom. For the transducer parameters used in our study, we obtained G = 56.6 and N = 0.0953 for nonlinear coefficient β = 4.5 and absorption coefficient α = 0.74 at the acoustic power of 15.68 W. It can be observed from Fig. 5[34] that the error between linear and nonlinear components in focal temperature rise is much smaller than 2% for G = 56.6 and N = 0.0953. Therefore, a linear model should be sufficient for temperature predictions[34] in the present study, although a nonlinear model might provide more accurate predictions for heat generation and temperature rise. However, for acoustic power higher than 115 W, the nonlinear effects in HIFU propagation and tissue heating are inevitable, and the acoustothermal effects of intensive cavitation[37–41] cannot be ignored. In order to analyse the temperature characteristics of HIFU therapy accurately, nonlinear Khokhlov–Zabolotskaya–Kuznetsov equation (KZK)[42,43] or spheroidal beam equation (SBE)[44,45] should be applied in future studies. In addition, to take into account blood flow and tissue inhomogeneity, more realistic models[46] with the properties closer to living tissues should be developed to obtain more accurate efficacy monitoring and dose control in HIFU therapy.
In this study, the principles of the proposed technology of treatment efficacy monitoring and dose control for HIFU therapy are based on the relationship between temperature and electrical impedance of tissues and the significant change in conductivity during tissue thermocoagulation. The RIV of the model can be used to monitor the temperature induced conductivity variation in the focal region. This measurement technology can separate electrical measurement from acoustic field completely, which is useful for avoiding the interference induced by acoustic impedance variations in tissues in the process of HIFU therapy. This work also confirmed that the dependencies obtained for RIV, RIVR, and treatment time are not affected by variations in the base electrical impedance of the phantom models of different shape and size; the differences are introduced only in fitted coefficients. Therefore, further studies on the coefficients for practical applications should be conducted to track the parameters of actual human bodies. In addition, real-time electrical impedance measurement system with high precision should also be designed to promote clinical applications of the proposed technology in treatment efficacy monitoring and dose control during HIFU therapy.
6. ConclusionIn conclusion, theoretical and experimental studies on temperature monitoring and efficacy evaluation in HIFU therapy were conducted based on the temperature–impedance relation using RIV measurements. A comprehensive system of HIFU therapy and impedance measurement for a cylindrical phantom was established. The distributions of acoustic pressure, temperature, conductivity, current density, and electrical potential at various acoustic powers were simulated. It was demonstrated that RIV increased linearly with rising treatment time at a fixed acoustic power, and RIVR exhibited a linear dependence on the acoustic power. To reach HIFU treatment efficacy, the required RIV was found to be inversely proportional to the acoustic power, while the required treatment time showed the inverse proportionality to the square of the acoustic power. Consequently, RIV and RIVR can be used to indicate treatment state, estimate acoustic power, and realize treatment time control in HIFU therapy. The favourable results provide the basis for real-time noninvasive temperature monitoring and efficacy evaluation, and also demonstrate the feasibility of accurate dose control in HIFU therapy.