† Corresponding author. E-mail:
The intensity distribution in Fresnel diffraction through a slit includes numerous small fluctuations referred to as ripples. These ripples make the modelling of the intensity distribution complicated. In this study, we examine the characteristics of the Fresnel diffraction intensity distribution to deduce the rule for the peak position and then propose two types of quantum-mathematical models to obtain the distance between the edge and the peak point. The analysis and simulation indicate that the error in the models is below 

Diffraction by a slit is a widely known phenomenon and has been observed in many fields, such as x-rays,[1–4] profile parameter measurement,[5,6] and metallic film measurement.[7] Analyses of this phenomenon, thus far, are mainly focused on far-field Fraunhofer diffraction[8–10] and near-field Fresnel diffraction by a single edge, because their intensity distributions are simple. In contrast, the present study reveals that the Fresnel diffraction by a slit has a considerably more complex intensity distribution.
A number of studies have described the calculation of the Fresnel diffraction intensity pattern.[11–18] Extreme points of the intensity pattern are used in many applications of Fresnel diffraction. For example, reference [19] makes use of the technique of locating the minimum to measure large-size parallelism, and reference [12] uses the expression of the location of extreme points to describe the focal effect of Fresnel diffraction by a slit.
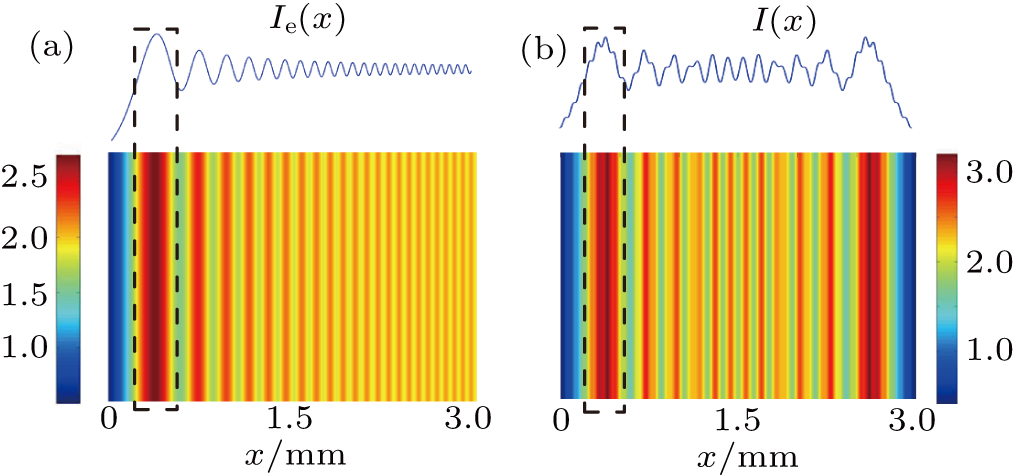
In Fresnel diffraction, the shape of the diffraction object and the diffraction pattern exhibit a fair degree of similarity. On this basis, we expect that the relation between the edge and some feature points of the intensity pattern could be used to measure the profile of the diffraction object. The peak with the strongest signal in the pattern is used as the feature point. Figure
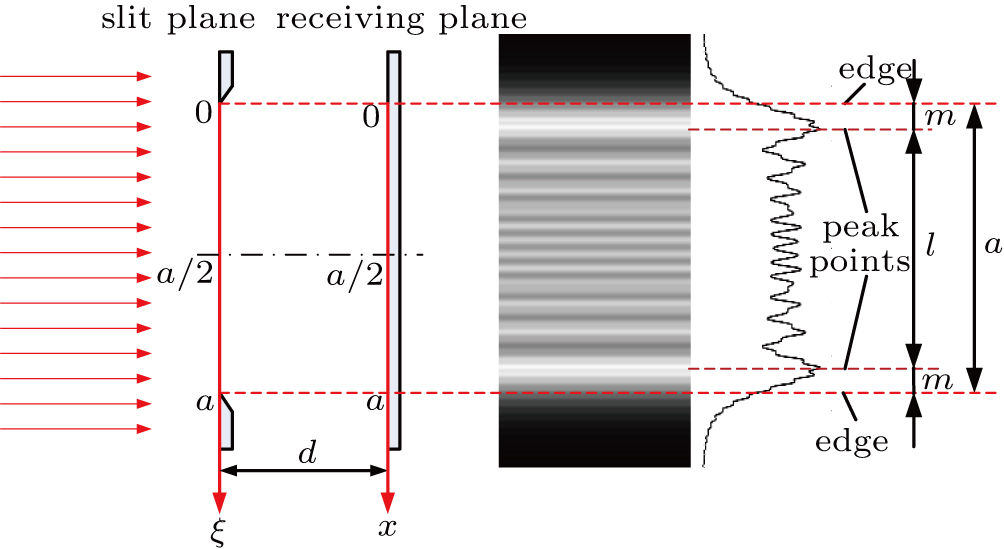 | Fig. 1. (color online) Coordinate system and intensity pattern of the Fresnel diffraction by a slit with λ = 650 nm, a = 3 mm, and d = 300 mm. |
If the distance l between the two peak points and the accurate distance m between the edge and the peak points are determined, then the two edges of the slit can be located, and the slit width a can be measured using the formula 
In Fig.
All the equations in this paper are based on the coordinate system shown in Fig.
According to the analysis by Southwell,[20] the Fresnel approximation for collimated propagation is sufficiently accurate for a large scope of 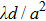
In this paper, we consider that the models for the Fresnel diffraction by a slit and a single edge are similar; therefore, we discuss the Fresnel diffraction model by a slit based on that with a single edge.
From Ref. [21], the expression for the Fresnel integral is
 |


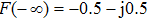
In Ref. [21], the intensity of the Fresnel diffraction by a slit can be expressed in the form of the Fresnel integral under Fresnel approximation. In this study, we alter the expression in accordance with the variables and coordinate system shown in Fig.
 |
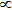


In this study, it is convenient to introduce dimensionless variables[12] such as 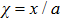

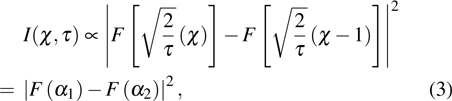 |
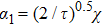
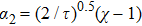
On substituting 
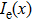
 |
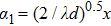
From Eqs. (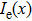
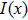

By repeating the above process for various values of d (diffraction distance), a series of intensity patterns are obtained. We produce a series of patterns for a single edge and then obtain the density pattern of Fresnel diffraction by a single edge in the 
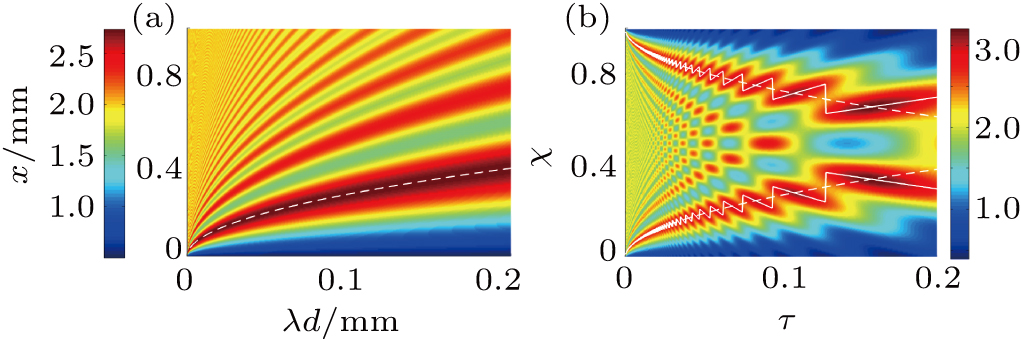 | Fig. 3. (color online) (a) Density pattern of the Fresnel diffraction by a single edge in the 
|
The single edge can be seen as a special slit where 
In Fig.
According to Ref. [12], the white dotted line shown in Fig. 
 |
The expression for m (distance between the peak point and the edge) can be obtained using two methods. In the first method, we deduce the accurate locations of the peak points using the formula for deviation and then obtain the required expression. In the second method, we obtain the expression using the characteristics of the track of the peak points represented by the white solid broken line in Fig.
From Eqs. (
 |
In the intensity curve shown in Fig. 



 |

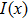
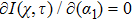
On taking the first derivative of Eq. (
 |
 |
 |
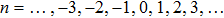
According to Eq. (
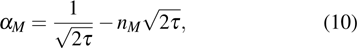 |

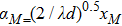
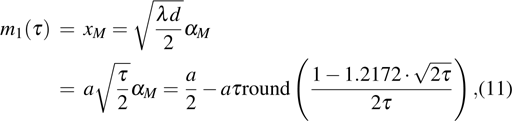 |

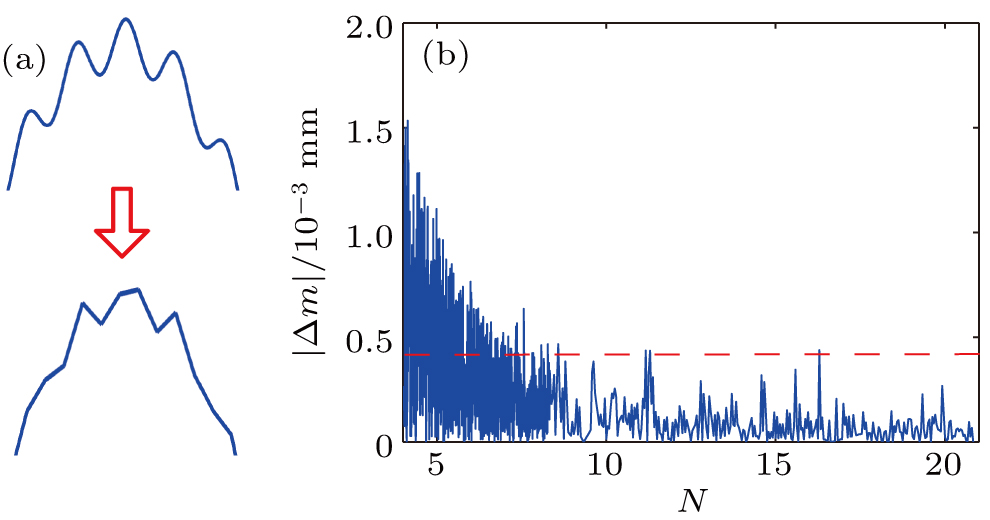
Furthermore, we detect the peak position based on the characteristics of the track of the peak points of the slit represented by the white solid broken line shown in Fig.
The existence of fluctuations in Fig.
As shown in Fig. 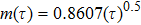
Moreover, figure
We use Eq. (

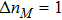
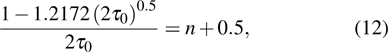 |
 |

Furthermore, from Eq. (

 |
Based on Eqs. (
 |

To numerically prove the viability of Eqs. (
 | Fig. 5. (color online) Error of Eqs. ( |
Figure 


Figure
We denote the pixel size of the CMOS as s. Thus, the sampling size of the main peak is
 |
Figure 
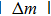
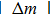

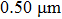
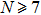
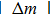
We can deduce the ranges of d and a that are suitable for our method using some application conditions. The conditions include the requirements for the value of 
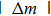



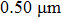



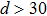
In summary, we can obtain suitable ranges for d and a for our method using 


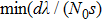
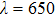

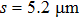
Figure
In Fig. 
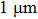

A plane parallel plate is one of the simplest lateral shearing interferometers used to obtain qualitative work in a laboratory, and we use it to focus the collimator. The shearing interferogram is shown in Fig.
We change the diffraction distance d from 100 mm to 500 mm by moving the two-dimensional translation machine with an interval of 5 mm. In order to enhance the SNR, 30 figures are acquired continuously for every value of d, and the mean figure is obtained using the following calculation. Finally, we obtain 81 mean figures, six of which are shown in Fig.
The corresponding values of d and N for λ = 650 nm, a = 3 mm, and 
| Table 1.
Values of τ and sampling size N for various d (mm). . |
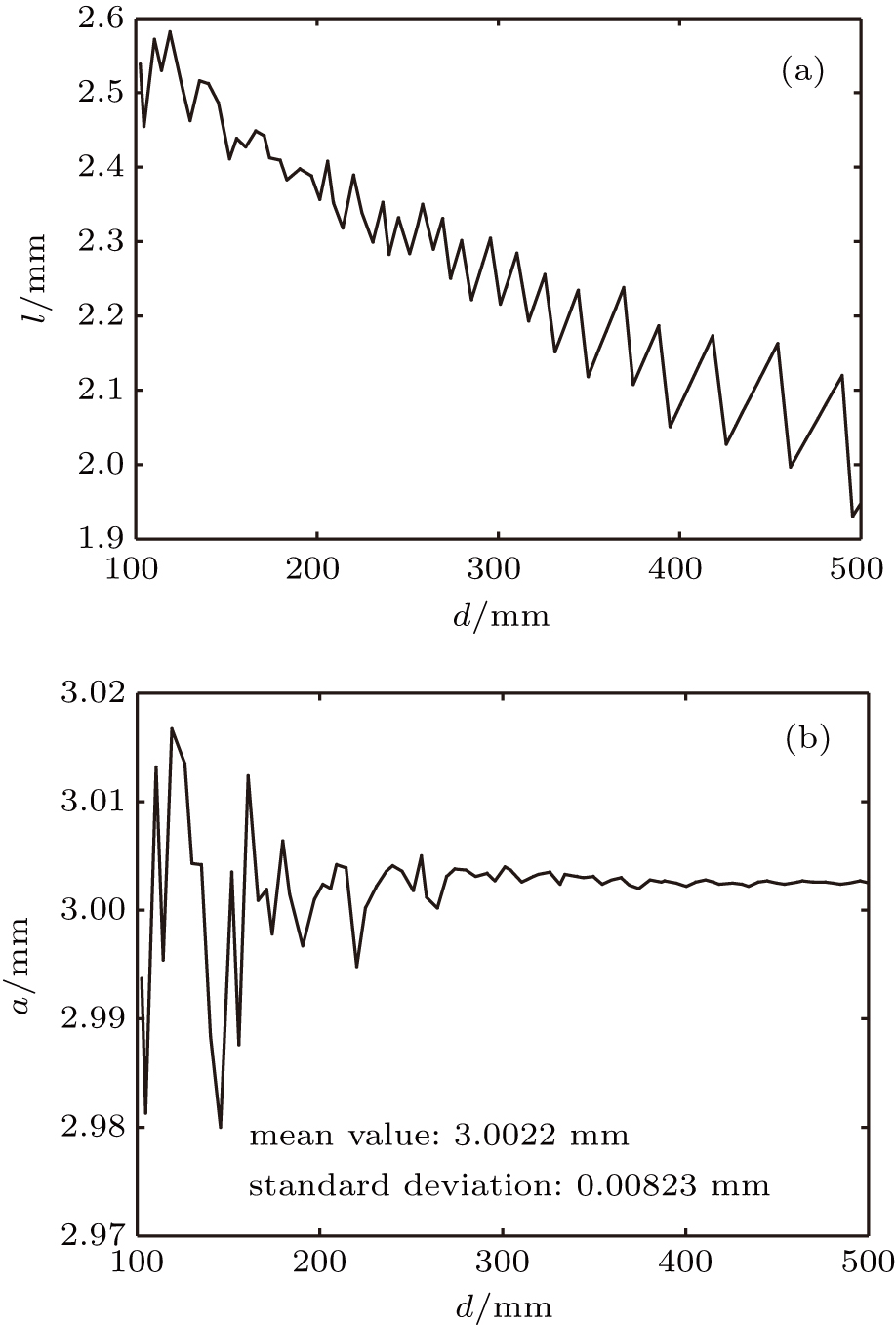
In the beginning, we use all the 81 mean figures for the calculation, and obtain 81 values of l to plot the curves d–l (d is the diffraction distance, l is the distance between the two peak points), as shown in Fig.
From Eq. (
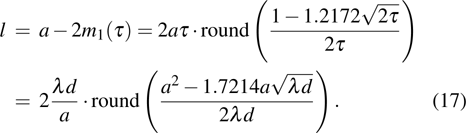 |
From Fig. 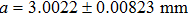

Furthermore, in order to verify the accuracy of Eqs. (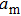

In Fig. 
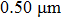
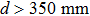
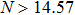
From Fig.
| Table 2.
Mean values and standard deviations. . |
From Table 
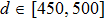
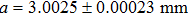
Overall, the experimental values of m are in good agreement with Eqs. (


In summary, we numerically deduce the intensity distribution of the Fresnel diffraction by a slit and propose two types of expressions for the edge and peak points. The simulations suggest that the error of the expression is approximately less than 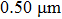

We also use an expression to detect the contour of the slit. A slit with a nominal width of 3 mm is used, and the experimental data reveal that the repeatability error of the measurement decreases as d increases, and it reaches 
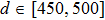
In future research, instead of a slit, we intend to use an aspheric surface as the diffraction object and suggest a new method for testing the aspheric surface by detecting the peak point of the corresponding Fresnel diffraction pattern.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] |