Cite this Article
Zhang Xiao-Hang, Xu Xin-Ye. Development of adjustable permanent magnet Zeeman slowers for optical lattice clocks. Chinese Physics B, 2017, 26(5): 053701  
Permissions
Development of adjustable permanent magnet Zeeman slowers for optical lattice clocks
Zhang Xiao-Hang, Xu Xin-Ye †
State Key Laboratory of Precision Spectroscopy and Department of Physics, East China Normal University, Shanghai 200062, China

 

† Corresponding author. E-mail: xyxu@phy.ecnu.edu.cn

Abstract

We develop a permanent-magnet Zeeman slower with adjustable magnets along the longitudinal and radial directions. Produced by four arrays of cylindrical magnets, the longitudinal magnetic field in the slower is tunable if relevant parameters vary, for example, laser detuning or intensity. The proposed Zeeman slower can be reconfigured for Sr atoms. Additionally, we demonstrate that the residual magnetic field produced by the permanent magnets in the magneto-optical trap region can be as small as 0.5 Gs.

PACS: 37.10.De;32.60.+i;07.55.-w
Keyword:permanent magnet;Zeeman slower;laser cooling;optical clock
1. Introduction

Divalent atoms such as ytterbium (Yb) and strontium (Sr) atoms are commonly employed in optical lattice clocks because they have ultra-narrow linewidth clock transitions.[1–5] To provide a good clock signal with high signal-to-noise ratio, hot atoms must be slowed for being captured into a magneto-optical trap (MOT). For divalent atoms, whether they source from hot metal vapor in ovens or discharges such as metastable helium atoms, a Zeeman slower is required by most experiments where optical lattice clocks are used.[6,7] During decelerating in the Zeeman slower, the atoms interact with a specified cooling laser beam in a gradient magnetic field. Traditional Zeeman slowers are comprised of current-carrying coils through which the atomic beam passes; however, they are rather complicated to build, as a steady current source and a water-cooling system are needed. Recently, Zeeman slowers with permanent magnets instead of coils have received special attention.[8–12] In this kind of slower, the gradient magnetic field is produced by the permanent magnets placed at specified positions. Hence they are easy to construct, adjustable, and inexpensive, requiring no water cooling or power supply; the only disadvantage is that the resultant magnetic field cannot be switched off.[13,14]

Unlike traditional slowers with coils, the magnetic field in a permanent-magnet Zeeman slower can be perpendicular or parallel to the atomic beam as needed.[15,16] The former determines the transverse field (TF) design and the latter the longitudinal field (LF) design. Recently, a group in the National Physical Laboratory (London, UK) has prototyped both designs built with cylindrical permanent magnets.[9] Fields produced by spherical and annular permanent magnets have also proved feasible for a Zeeman slower.[10,11,17]

In this paper, we describe a Zeeman slower composed of four arrays of permanent magnets that are positionally adjustable. First, we present the theory of this design and examine the desired longitudinal component of the magnetic field distribution. Second, we confirm in experiment the feasibility and accuracy of the design for Yb lattice clocks. Furthermore, we demonstrate that the magnetic field distribution can be modified with small adjustment in magnet position if laser detuning occurs or laser intensity varies. Finally, this Zeeman slower is shown to be capable of slowing other divalent atoms such as Sr atoms.

2. Presentation of the design
2.1. Theoretical description

The Zeeman slowing technique involves a process whereby a beam of atoms interacts with a monochromatic counter-propagating laser beam in a gradient magnetic field.[18] The Zeeman slower must produce a spatially varying magnetic field to compensate for the Doppler shift in the atoms decelerated by the counter-propagating laser beam. The atom deceleration can be treated classically. Setting the Cartesian coordinate Oz along the direction of the atom beam, this deceleration is then given as

where is the photon scattering rate, the local detuning depending on the longitudinal velocity of the atoms, B(z) the corresponding magnetic field, the frequency detuning of the cooling laser, the wave vector of the cooling laser beam of wavelength λ, the effective magnetic moment of the transition used in laser cooling with and being the Landé g-factor and magnetic quantum number, respectively, corresponding to the ground state (g) and excited state (e), and the Bohr magneton. The maximum local on-resonance saturation parameter s0 of the atomic transition is defined by with I and being the peak intensity and saturation intensity of the cooling laser, respectively. At zero detuning, the maximum deceleration is . However, an efficiency parameter is induced to ensure that the slowing process is robust because the magnetic field does not exactly compensate for the Doppler shift. The form of the magnetic field distribution derived from Eq. (1) is determined by the detuning of the laser beam during laser cooling. To reduce the amplitude of the maximum magnetic field in the slower, a negative detuning cooling laser is employed, and the magnetic field distribution can be derived as
where is a constant, the detuning modification, the longitudinal component of velocity on the assumption that during slowing the deceleration is approximately constant. Given v0 and as the initial and final velocity of the atom respectively, the length of the Zeeman slower estimated from kinematics is , and hence is determined by deceleration a, provided the temperature of the atomic oven is fixed. The final velocity is usually set by the capturing capability of the MOT.

2.2. LF design for a permanent-magnet Zeeman slower

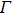
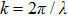
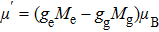
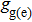
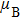
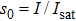
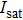
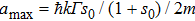
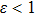
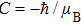
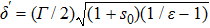
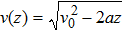
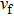
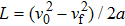
Because the saturation intensity of the cooling laser beam for a neutral atomic clock is relatively large, having a very high laser intensity is usually impractical. Therefore, an LF design can efficiently use the beam and hence is preferable to a TF design. In a magnetic dipole design, cylindrical permanent magnets treated as magnetic dipoles produce the desired magnetic field in the slower. The magnets need to be small enough compared with the distance between the magnet and the atomic beam. In the LF design, the magnetic dipoles are parallel to the Z axis, and the field overlaps with the atomic beam. In general, the magnetic field distribution of a magnetic dipole placed at the origin is expressed in Cartesian coordinates as follows:

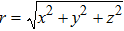
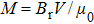
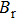
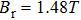
where and μ0 is the magnetic permeability; the magnetic moment of the dipole is given by with being the remanent flux density and V the volume of the magnet. The magnet is made of neodymium iron boride, with remanent flux density (Serial number, 50, SuZhou JunYon Auto Accessories Co. Ltd, China). In the slower, the total magnetic field distributed along the Z axis is the sum of the longitudinal magnetic field component of each magnet,

To calculate the position of the magnet, we introduce the horizontal spacing between two successive magnets 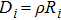, where Ri is the perpendicular distance between the magnet and atomic beam axis. To minimize the ripple in the magnetic field distribution, a value for ρ is chosen. In the slower, the four linear arrays of magnets (normally there are used two arrays) are symmetrically located about the Z axis to increase the transverse uniformity of the longitudinal magnetic field. During its assembly, the horizontal positions of the group of magnets at exit of atoms are determined first, then the horizontal distances between the remaining magnets and the end of slower are calculated.[19] As described in previous work, the magnet moment is also optimized by selecting magnets of a proper volume.[19] When assembling the slower, the initial positions of the magnets with normal magnetic moments are calculated. Then the magnets positioned too close to or too far from the atomic beam should be changed. This configuration has several advantages over those of similar work. First, the end position of the slower is predetermined; therefore the position of the MOT can also be predetermined. Second, the positions of the magnets at the exit of atoms in the slower can be adjusted to ensure that the atoms can be captured by the MOT, and the effect of adjusting the magnetic field distribution in the slower is acceptable. Additionally, in this design, the volume of each magnet can be changed to reduce the width of the slower and improve the accuracy of the magnetic dipole design.

3. An adjustable LF design for Yb atomic clocks
3.1. Simulation result of the magnetic dipole model

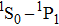
Regarding the deceleration of Yb atoms, the theory of small adjustable slowers and their optimal setup has been studied in previous work.[19] From Eq. (2), the detuning of the -polarized cooling laser beam is estimated to be −380 MHz, which is to reduce the maximum magnitude of the magnetic field needed in the slower. The polarization is chosen to extract the atoms from the deceleration process at the end of the slowing process. To reduce the length of the slower, the maximum saturation parameter of the cooling laser beam is set to be 3 because the cooling transition for Yb atoms has a relatively large saturation intensity of 60 mW/cm2.[20] Although the deceleration process is most stable when the coefficient ε is set to be 0.75, ε is set to be 0.9 to reduce the length of the slower.[21]

With the parameters of the slower determined, we examine in simulations the field distribution produced, given the positions of the magnets in the permanent-magnet Zeeman slower. These magnets are inexpensive and commercially available products. Their magnet moments can be verified by a Hall probe Gauss meter prior to simulation. The positions of the magnets are nonlinearly determined by using software subject to minimizing the deviation between the simulated magnetic field and the desired magnetic field. The calculation indicates that the total number of magnets needed in the slower is 32, i.e., eight groups of four magnets longitudinally arranged. Each group of magnets is positioned symmetrically around the beam (Z axis). In accordance with the assembly procedure stated above, the exit of the atoms in the slower is positioned at Z = 150 mm; the positions of the magnets in the X0Z plane are indicated in Table 1. The slower is 153.1 mm long and 85.4 mm wide at the widest point.

Table 1.

Calculated positions and sizes of magnets.

.

With the positions of the magnets determined, the sizes of the magnets need to be evaluated. Three sets of magnets with different radii, heights, and magnet moments are used: i) 5 mm, 4.5 mm, and M = 0.276 A m2 for the smaller magnets; ii) 9.5 mm, 9 mm, and M = 1.848 A m2 for the normal magnets; and iii) 10.5 mm, 9 mm, and M = 2.475 A m2 for the larger magnets. To avoid placing the magnets too close to the atomic beam, the second group is composed of the larger magnets. The sixth and seventh groups need to be composed of the smaller magnet to reduce the width of the slower from nearly 200 mm to less than 90 mm. The full length of the slower is about 163 mm, with a width of about 105 mm.

3.2. Assembling the permanent-magnet Zeeman slower

Prior to assembling the slower, we numerically calculate the magnetic field produced by the magnets to confirm the calculated positions of the magnets. In Fig. 1(a), the magnetic field distribution along the Z axis (black solid line) simulated using the one-dimensional magnetic dipole design (Table 1) accord with the desired magnetic field distribution (black triangles), which is ideal for slow atoms. After positioning the magnets, the longitudinal component of the magnetic field distribution in the center of the slower is measured by using a Hall sensor (Fig. 1(a)). The measured result (red circles) is in good agreement with the simulated and desired results, which confirms the accuracy of the magnetic dipole design. However, there is a small deviation of the measured curve from the simulated curve, which is explained as follows. First, if the size of the magnet cannot be ignored when compared with the distance between the magnet and atomic beam axis, the precision in the magnetic dipole design cannot reach the anticipated one. The magnets are set to be a little closer to the atomic beam to reduce the width of the slower (Table 1). Second, there are slight variations in hand-held Gauss-meter measurements and the magnet position measurements. Furthermore, any variation in the magnetic moment of the magnets of the same size would contribute some deviation.

Fig. 1. (color online) (a) Simulated (black solid line), measured (red dotted line), and desired (black solid-triangle-dotted line) magnetic field distributions. Inset shows the transverse distribution of the magnetic field at the end of the slower. (b) Side view of the Zeeman slower.

When assembling the Zeeman slower, the magnetic field distribution transverse to the beam needs considering. Because of the size limitation of the Hall sensor, the transverse field distribution at the end of the slower is measured in steps of 5 mm (see the inset of Fig. 1(a)). The variation in the magnetic field over a 10 mm range is about 1.6%, which is in accordance with theoretical estimate.[19] A side view of the slower (Fig. 1(b)) shows the magnets (silver cylinders) fastened with copper screw caps; they can be adjusted along the longitudinal and radial directions. In the center of the apparatus, there is a pipe made of nonferromagnetic material through which the atoms pass. The aluminum frame is pre-mounted in the ultra-high vacuum system, and the magnets are fastened after the system has been baked. Furthermore, a similar Zeeman slower is also built to determine magnet positions of the slower in the experimental setup.

3.3. Modified magnetic field distribution

With the permanent-magnet Zeeman slower assembly, environmental influences on the magnetic field in the slower needs consideration. As no magnetic field shield is used, the magnetic field produced by the MOT coils is also considered in simulations. We calculate the magnetic field distribution from the beginning of the slower to the MOT region by using Eqs. (3) and (5). The field of the coils terminates the deceleration especially when the atoms approach to the MOT. The longitudinal magnetic field produced by a single coil of radius R perpendicular to the X axis and centered at is given as[22]

where I is the current and D the distance between the coils and the Z axis; and are the complete elliptic integrals of the first and second kind, respectively, with .[9] Setting parameter values of the MOT coil to match the performance of the MOT given in Ref. [20] yields the longitudinal magnetic field plotted in Fig. 2. According to previous work, positioning the MOT region at Z = 233 mm is beneficial, as the conditions for cooling are similar.[19]

Fig. 2. (color online) Simulated magnetic field distribution produced by an MOT coil.

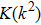
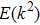
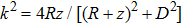
In simulating the atom trajectories, we find that the magnetic field from the MOT coil would stop the deceleration of most of the atoms before they reach the MOT region. By analyzing the relationship between atom trajectories and magnet positions, the final group of magnets (group 8 in Table 1) is moved to 48.5 mm to ensure that the atoms decelerate and enter into the MOT region. This group of magnets functions like a compensation coil in the traditional Zeeman slower. The corresponding magnetic field distribution proposed in Fig. 3 is in good agreement with the measured result. The magnetic field at Z = 233 mm is about 0.5 Gs, which is easy to compensate for. A comparison between the curves in Fig. 3 and Fig. 1(a) shows that the magnetic field in the MOT region decreases significantly: the further the magnets move away from the atomic beam axis, the more the magnetic field decreases. With the experimental apparatus made of nonferromagnetic material, its magnetization can be ignored. The photoelectric device is also positioned far from the atoms in the MOT to avoid the influence of residual magnetic field. Three compensation coils placed around the chamber can easily compensate for small residual magnetic field produced by the slower or surroundings, suggesting that, with appropriate conditions and careful simulation of the magnetic field, this design setup requires no magnetic shield.

Fig. 3. (color online) Measured (red dotted line) and simulated (black solid line) magnetic field modified through the adjustments of the magnets.

From Figs. 2 and 3 it follows that the magnetic field distributions are quite different. The modified magnetic field must also meet specifications of the slower. Atomic trajectories for the simulated magnetic field given in Fig. 3 are calculated and presented in Fig. 4. Atoms with a velocity between 90 m/s and 310 m/s are decelerated to velocities below the capture velocity of the MOT region. By the analysis in Ref. [19], the slowing efficiency is around 15.5%, which is acceptable compared with those of other permanent-magnet Zeeman slowers.

Fig. 4. (color online) Simulated trajectories of atoms under different magnetic field distributions.
3.4. Adjustment of the permanent-magnet Zeeman slower

The adjustment of the magnetic field distribution to the value within the proper range is advantageous when experimental conditions vary. As Eq. (2) indicates, the variations in detuning and intensity of the cooling laser would change the magnetic field distribution that is desired. If either changes during an experiment, the efficiency of the slower will decrease. These variations can be calculated and expressed as adjustments of magnet positions. For a detuning of 30 MHz, a change within 5 mm at magnet position is all that is required. In Fig. 5, having adjusted the positions of the magnets for a cooling-laser detuning of −350 MHz, the measured field is seen to be still in good agreement with the simulated curve. The result indicates that a suitable adjustment for laser detuning can be compensated for during the experiment.

Fig. 5. (color online) Simulated (black solid line) and measured (red dotted line) magnetic field distribution when the detuning of the cooling laser is −350 MHz.

Similarly, the magnetic field distribution can also be adjusted to match a laser intensity that varies. In our case, supposing that the saturation parameter ranges from 3.0 to 2.5, a change in magnet position is viable. Compared with laser detuning, a variation in laser intensity is more common during experiment. While the maximum saturation parameter of the cooling laser decreases, the required gradient of the magnetic field distribution also decreases. Therefore the slowing efficiency of the slower decreases as the gradient magnetic field is unable to slow atoms sufficiently for capture by the MOT. For this design, this kind of change can be easily compensated for. Compared with the results in Fig. 2, the influence of the MOT coils needs to be taken into account. For a detuning of −380 MHz and saturation parameter of 2.5, the magnetic field distribution and corresponding measured results (Fig. 6) are very close to each other. In addition, the length of the slower has changed only slightly.

Fig. 6. (color online) Simulated (black solid line) and measured (red dotted line) magnetic field distributions when the saturation parameter of the cooling laser is set to be 2.5.

The above results from experiments prove that the permanent-magnet Zeeman slower can be adjusted to compensate for laser detuning or intensity variation. The slower can produce a magnetic field distribution only if its slope and maximum amplitude are less than their largest values that the magnet can produce. Moreover, the magnets can be replaced, thereby easily eliminating the need to re-bake the slower even if the desired magnetic field is changed.

4. Common applications for divalent atoms

As divalent atoms have similar energy-level structures, the permanent-magnet Zeeman slower presented here is also versatile for applications with other atoms (Sr, Mg, Ca). We build a similar slower for Sr atoms and measure the resultant magnetic field. In this case, the scattering rate is about , which is similar to that for Yb atoms despite Sr atom being much lighter than Yb atom. Hence the deceleration is much larger for Sr atoms than for Yb atoms given by the same laser intensity and detuning. Setting an efficiency parameter ε of 0.7 and saturation parameter s of 3, the slowing length is still about 15 cm. To reduce the maximum magnetic field in the design, the detuning of the cooling laser is set to be −550 MHz. The simulated magnetic field and the measured magnetic field (Fig. 7) are also in good agreement with the desired value, but the magnets used in Sr clocks are not the same as those for Yb clocks. In the slower for Sr atoms, the seventh group of the magnets must be replaced by magnets with magnetic moment M = 1.848 A m2 for the designed magnetic field to be approximately the same as the simulated field.

Fig. 7. (color online) Simulated magnetic field distribution (black solid line) and measured results (red dotted line) for Sr atoms.

The experimental results (Fig. 7) indicate that this slower design can be used for different divalent atoms and even for the same experimental apparatus if the desired magnetic field distributions are similar. Moreover, the magnet positions can be modified manually to capture as many atoms as possible during experiment.

5. Conclusions and perspectives

A simple and adjustable permanent-magnet Zeeman slower is built and examined. Compared with the magnetic dipole design used in previous work, this modified configuration improves the performance of the Zeeman slower. The length of the slower is about 15 cm, which is the shortest in similar designs for Yb optical lattice clocks. The measured magnetic field distributions accord with the simulated results, and the uniformity of the longitudinal magnetic field in transverse cross sections is confirmed, verifying the accuracy of the model. The adjustability of the slower is demonstrated by varying the detuning and intensity of the cooling laser, and the magnetic field distribution can be altered by adjusting magnet positions. Furthermore, the universality of the design is evident by adjusting magnet positions to produce a magnetic field distribution suitable for Sr optical lattice clocks. That is, this slower is suitable for most divalent atoms, thereby enabling the miniaturizing of neutral atomic optical clocks and offering the portability of space-borne optical lattice clocks.

As the magnets used are commercially available, the cost of the slower is low. Furthermore, the accuracy of the model described can be improved by employing magnets with larger magnetic moments. Their sizes would then be much smaller than their distances to the atomic beam axis, thereby conforming to the assumption of the magnetic dipole model. Thus, in the future, improvements in performance of the slower and reduction in the slowing length can be made.

Reference
[1] Nemitz N Ohkubo T Takamoto M Ushijima I Das M Ohmae N Katori H 2016 Nat. Photon. 10 258
[2] Nicholson T L Campbell S L Hutson R B Marti G E Bloom B J McNally R L Zhang W Barrett M D Safronova M S Strouse G F Tew W L Ye J 2015 Nat. Commun. 6 6896
[3] Hinkley N Sherman J A Phillips N B Schioppo M Lemke N D Beloy K Pizzocaro M Oates C W Ludlow A D 2013 Science 341 1215
[4] Chen N Xu X Y 2015 Laser Phys. Lett. 12 015501
[5] Zhang X H Zhou M Chen N Gao Q Han C Y Yao Y Xu P Li S Y Xu Y L Jiang Y Y Bi Z Y Ma L S Xu X Y 2015 Laser Phys. Lett. 12 025501
[6] Metcalf H J van der Straten P 1999 Laser Cooling and Trapping New York Springer–Verlag 73 85
[7] Dedman C J Nes J Hanna T M Dall R G Baldwin K G H Truscott A G 2004 Rev. Sci. Instrum. 75 5136
[8] Ovchinnikov Y B 2007 Opt. Commun. 276 261
[9] Hill I R Ovchinnikov Y B Bridge E M Curtis E A Gill P 2014 J. Phys. B: At. Mol. Opt. Phys. 47 075006
[10] Lebedev V Weld D M 2014 J. Phys. B: At. Mol. Opt. Phys. 47 155003
[11] Wang Q Lin Y G Gao F L Li Y Lin B K Meng F Zang E J Fang Z J Li T C 2015 Chin. Phys. Lett. 32 100701
[12] Cheiney P Carraz O Bartoszek-Bober D Faure S Vermersch F Fabre C M Gattobigio G L Lahaye T Guéry-Odelin D Mathevet R 2011 Rev. Sci. Instrum. 82 063115
[13] Hill I R Ovchinnikov Y B Bridge E M Curtis E A Donnellan S Gill P 2012 European Frequency and Time Forum April 23–27, 2012 Gothenburg 545 10.1109/EFTF.2012.6502439
[14] Reinaudi G Osborn C B Bega K Zelevinsky T 2012 J. Opt. Soc. Am. 29 4
[15] Ovchinnikov Y B 2008 Eur. Phys. J. Special Topics 163 95
[16] Ovchinnikov Y B 2012 Opt. Commun. 285 1175
[17] Nath P Chandrana C K Dunkerley D Neal J A Platts D 2013 Appl. Phys. Lett. 102 202409
[18] Barrett T E Dapore-Schwartz S W Ray M D Lafyatis G P 1991 Phys. Rev. Lett. 67 3483
[19] Zhang X H Xu X Y 2016 Laser Phys. 26 075501
[20] Xu X Y Wang W L Zhou Q H Li G H Jiang H L Chen L F Ye J Zhou Z H Cai Y Tang H Y Zhou M 2009 Front. Phys. China 4 160
[21] Molenaar P A van der Straten P Heideman H G M 1997 Phys. Rev. 55 605
[22] Bergeman T Harold G E Metcalf J 1987 Phys. Rev. 35 1535