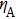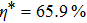Time–energy high-dimensional one-side device-independent quantum key distribution
1. IntroductionUsing quantum key distribution (QKD), two distant communication parties, called Alice and Bob, can generate secret keys, with the security based on the fundamental laws of quantum mechanics.[1, 2] Although QKD is unconditionally secure, some gaps exist in theoretical and practical security of QKD due to imperfections of QKD devices. Using these security loopholes, the eavesdropper Eve can perform some attacks, such as faked state attacks,[3,4] after-gate attacks,[5] dead time attacks,[6] and wavelength-dependent attacks.[7] Since the first QKD protocol, BB84 protocol,[8] was proposed, QKD gets quick development in theory and experiments,[9–13] and lots of work on eliminating these gaps have been done.[14–19]
One of the most promising approaches of eliminating these gaps is device-independent QKD (DI-QKD).[20,21] The security of DI-QKD is guaranteed by the observed violation of Bell inequalities[22] and it requires the minimal set of assumptions. However, to test the violation of Bell inequalities, detectors used in DI-QKD are required to ensure very high detection efficiencies.[21] Therefore, it is an extreme challenge to demonstrate DI-QKD in practice. To relax constraints of DI-QKD, some valuable proposals for QKD have been proposed as compromises between device-dependent QKD and device-independent QKD.
Based on dimension witnesses,[23] Pawłowski and Brunner[24] proposed a DI-QKD scenario with relaxed constraints, which is called semi-device-independent QKD (SDI-QKD), and proved its security against individual attacks. To remove detector side channel attacks, the idea of measurement-device-independent QKD (MDI-QKD)[25,26] is proposed and developed.[27–29] Some important aspects are studied in recent years.[30–33] Although those ideas can remove detector side channel attacks and double the secure transmittance distance, they require the perfect performance of the source. Furthermore, Branciard et al.[34] present a trade-off scenario, called one-side device-independent QKD (1sDI-QKD), between device-dependent QKD and device-independent QKD and analyze its security and feasibility by connecting the scenario with quantum steering.[35] 1sDI-QKD can be applied to some special conditions, e.g., establishing secret keys between a bank with its clients, where a bank can invest lots of money to set up reliable apparatus, while clients may use cheap and insecure terminals. In recent years, some relevant researches have been finished.[36–38]
However, in the original 1sDI-QKD, the photon information efficiency limits the rate of generation the key (no more than 1 bit per coincidence). Coding information in high-dimensional photonic degrees of freedom is a promising way to break the limitation. Furthermore, high-dimensional correlations can tolerate more noise.[39]
Some photonic degrees of freedom have been applied in HD-QKD, including position-momentum,[40] time–energy,[41–43] transverse momentum,[44] and orbital angular momentum.[45–47] Based on time–energy entanglement, Mower et al.[48] proposed a new high-dimensional QKD (HD-QKD) protocol using dispersive optics, which is called DO-QKD. Its security against collective attacks has been proven in Ref. [49] and its practical security analysis has been studied.[50–53] Recently, by deriving a novel entropic uncertainty relation for time and conjugate-time measurements using dispersive optics, Niu et al.[54] proved its security against general attacks.
In this paper, we extend time–energy high-dimensional code into 1sDI-QKD and propose a new protocol, so-called time–energy high-dimensional one-side device-independent QKD protocol (1sDI-HDQKD). Using the novel time–energy entropic uncertainty relation, we prove the security of our protocol against coherent attacks. By numerical simulation, we show that our protocol achieves more bits information per coincidence and requires lower detection efficiencies than the original 1sDI-QKD protocol. Then we relate the security of our protocol to violation of an EPR steering inequality.
The rest of this paper is organized as follows. In Section 2, we briefly describe the time–energy 1sDI-HDQKD protocl. In Section 3, we prove the security of our protocol against coherent attacks by time–energy entropic uncertainty relation. We connect our protocol with quantum steering in Section 4. Results of numerical simulation are shown in Section 5, and the conclusion is summarized in Section 6.
2. Protocol descriptionThe schematic of our protocol, the 1sDI-HDQKD protocol, is shown in Fig. 1. Our protocol is based on an entanglement-based 1sDI-QKD protocol with an untrusted source in Fig. 1(a) or with a trusted source in Fig. 1(b), which is equivalent to a prepare-and-measure 1sDI-QKD scheme.[34] We consider that Alice does not trust her measurement devices or she treats them as a black box, while Bob trusts his devices. Eve has the ability to completely control quantum channel but the classical channel is authenticated. In our protocol, particular, we use the result measured in time basis (
basis) by both Alice and Bob to extract a secret key, while results measured in conjugate-time basis (
basis) are used to estimate Eve’s information. Here we use spontaneous parametric down-conversion (SPDC) source to generate time–energy entangled states. The coherent time of the pulsed pump field is denoted by
. The correlation time bin duration between two entangled particles is denoted by δ. We denote the duration of a frame by
(
). The dimension d is determined by
. The protocol is described as follows.
State preparation and distribution For each distribution, the source prepares a time–energy entangled state within a
-duration frame. Then the source sends one particle of the pair to Alice and the other to Bob via the quantum channel.
State measurements For each frame, Alice and Bob select a basis between
basis and
basis at random and independent. Then they perform measurements in their chosen bases and record their outcomes respectively. Since Alice’s measurement apparatuses are untrusted, Eve has the ability to control whether the detector at Alice’s side click depending on her received state and measurement setting. Therefore, we cannot simply discard Alice’s no-detection events. Bob trusts his measurement apparatuses, which Eve cannot control. So we can safely consider only the cases where Bob gets detections.
Sifting After all signals are transmitted, both of them publish their basis choices over an authenticated public channel. They sift their raw keys only from correlated events acquired in
basis and use the corresponding measurement outcomes acquired in
basis for parameter estimation. Let
and
denote Alice and Bob’s raw keys respectively. The outcomes in
basis are denoted by
and
.
Postselecting Alice publish her no-detection events and then they can postselect their raw keys on the events that Alice gets detections. Then Alice and Bob get postselected bit strings
and
respectively. Discarded data are denoted by
and
. Let N denote the length of the strings
and
, and n denote the length of the strings
and
.
Post-processing After above steps, Alice and Bob perform parameter estimation and then test quantum steering. If they demonstrate quantum steering by the violation of an EPR-steering inequality, they apply error correction and privacy amplification (from Bob to Alice) on their data or abort the protocol.
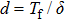
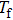
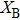
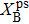
3. Security proof and key rateRecently, Niu et al.[54] proposed and proof a novel time–energy uncertainty relation for smooth entropies. By using the novel uncertainty relation, we present the secure key rate of our time–energy HD-1sDI-QKD. Noted that Alice’s measurement apparatuses are untrusted, the assumption that the devices are memoryless is needed as in Ref. [55].
Through the classical post-processing process, from the postselected n-bit strings
and
, Alice and Bob can generate a secret key of length
Here
is the smooth min-entropy of
, conditioned on Eve’s quantum side information
E;
[56] leak
EC is the leaked information in post-processing process.
According to the chain rule[57] and the data-processing[58] inequality for smooth min-entropies, we have the following relationship:
Using the novel time–energy uncertainty relation for smooth min-entropies,[54] we have
where the smooth max-entropy
measures the amount of information needed to reconstruct
given
with error probability bounded above by
ε, and
is the overlap between the time and conjugate-time measurement operator.
δ is the time bin duration and
is the magnitude of the group velocity dispersion (GVD) elements’ dispersion coefficient. Using the result of Ref. [
45], the smooth max-entropy follows the upper bound
where
dW is the corresponding
L1 code distance in the
basis and
obeys
Since the basis is selected randomly,
dW is the same as the value without postselection.
Substituting Eqs. (3) and (4) into Eq. (2), we obtain
Considering the imperfect reconciliation efficiency
, we have the equality[60]
Using the upper bound on the smooth max-entropy like Eq. (
4), we obtain
Then we obtain the length of secure keys
Considering the asymptotic limit of infinite key lengths, the fraction
of photons that Alice detects, given Bob detected one, can be treated as the detection efficiency of Alice, which is denoted by
. Then we can write the secure key rate in bit per coincidence (bpc) as
The positive raw key is the precondition of generating positive secret key. Considering raw key, the raw key rate can be written as
As is shown in Eq. (
11), the inequality “right side of Eq. (
11)
” is violated. More explicitly, the following inequality is violated:
On the other hand, positive raw key rate can be generated between Alice and Bob if and only if they check that they share entanglement, which amounts to demonstrating quantum steering. In the next section, we will show that equation (
12) is an EPR-steering inequality
[35] and equation (
11) demonstrates quantum steering.
4. Connection to EPR steeringWe first denote
,
in Alice’s measurement and for
and 2,
represents
and
, respectively. The similar definition is
in Bob’s measurement. Extending the proof in Ref. [34] using a local hidden state model,[35] the statistics of a local model can be measured by Alice and Bob and be decomposed as[61]
where
, with
ai and
bj denoting the experimental outcomes corresponding to measurements
and
, and
s denoting whether Alice gets a detection (
s = 1) or not (
s = 0). In case of no detection, Alice’s result
ai is chosen to be random bit values in our protocol and will contribute to the bit string
. The variable
λ represents Bob’s received quantum state. Bob’s statistics are identified by quantum mechanics:
, where
is a quantum state and set
are the positive operators that describe his measurements.
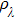
According to Eq. (13), we know that, for Alice, the way to obtain maximal information about Bob’s results is to get it through λ. By the conditional entropies, the result can be indicated as
Here
and
are the average conditional entropies of Bob’s measurement
respectively, under the knowledge of the result of
and of
λ, with
and
.
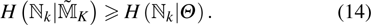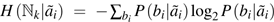
Then Bob’s statistics conditioned on λ are given by a quantum state assumption. So they must fulfill all quantum uncertainty relations, and particularly
Then using Eq. (
14), we obtain
Denoting
for
when s = 1 and
for
when s=0 and the corresponding probability is
, we have
Substituting the uncertainty relation
into Eq. (
16), we have
On the other hand, we have
Substituting Eqs. (
18) and (
19) in Eq. (
16), we get Eq. (
12). Thus equation (
12) defines an EPR-steering inequality.
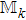
5. Numerical simulationBefore performing the numerical simulation, we should confirm some parameters.
According the time–energy uncertainty relation, we can determine the overlap
as[54]
The corresponding
code distance in the
basis can be bounded by
Here
is the upper bound on
, which is the mean-square difference of correlation time between entangled pairs measured in
basis. Due to excess noise
, we have
Consider a typical experimental setup, where a source sends maximally entangled states to Alice and Bob, through a depolarizing channel with time (conjugate-time) visibility
. With Alice’s detection efficiency
and dual-basis interferometry used in time–energy QKD,
[49] the excess noise can be determined by
where
is a function related to the visibility and the setting of interferometry
. Using results in Refs. [
49], [
54], and [
62], we can obtain thresholds of
and
as
The code distance determines if the QKD protocol is aborted or not, so we should choose a much bigger value than thresholds in order to have non-zero key rate. In the HDQKD protocol with two trustworthy parties, the value is set as 2.0.[54] In our protocol, it should not be less than that. All other parameters are taken from Ref. [54] and listed in Table 1.
Table 1.
Table 1.
 Table 1.
Parameters used in numerical simulation.
. | Table 1.
Parameters used in numerical simulation.
. |
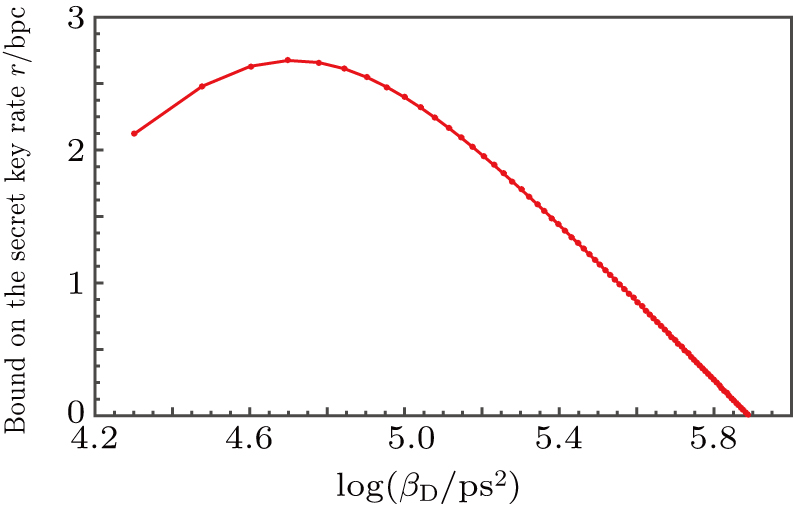
Figure 2 shows bounds on the secret key rate as a function of Alice’s detection efficiency
for different code distances. Compared with the original 1sDI-QKD protocol, our protocol requires much lower Alice’s detection efficiency and achieves more secure bits information per coincidence. For
in Fig. 2, one gets a positive secret key rate for all
. This means that Alice’s measurement apparatus can tolerate more Eve’s intrusion (less events that the
basis is actually chosen by both Alice and Bob).
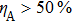
It seems that increasing the GVD coefficient
will increase the entropy uncertainty so the secret key rate will be increased. However, the error rate, quantified by
, between Alice and Bob’s raw keys will also increase with increasing
. To show the relation clearly, we consider a special condition, Alice’s detection efficiency
when
without changing other system parameters. Figure 3 plots the secret-key rate versus the GVD coefficient
.
From Fig. 3, we can see the secret key rate is not always increased with
increasing. Under above parameter settings, the maximal secret key rate is 2.7 bits per coincidence with the GVD coefficient
.
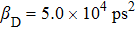
For clarifying the relation among the secret key rat r, Alice’s detection efficiency
, and the GVD coefficient
, figure 4 is plotted.
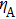
Then we consider the performance of our protocol in the standard optical fiber channel. For simplifying the analysis, we adapt the scenario shown in Fig. 1(a) and assume the on-demand single-photon source. We set propagation loss α =0.21 dB/km and the channel transmittance
, where L is the transmission distance. Alice’s average detection efficiency is denoted by
. All other parameters are the same as those in table 1. After postselection and post-processing processes, we have the secret key rate
 | |
Figure 5 plots the bound on the secret key rate in the optical fiber channel. All detection efficiencies are chosen from thresholds in DI-QKD and original 1sDI-QKD. Compare with recent results in Ref. [38], our protocol performs much better no matter in the secure bits per coincidence or the transmission distance. Note that, in our protocol, the losses between the source and Bob’s side do not affect the security of the protocol due to postselecting process. Eve can only decrease the key rate proportionally to the decrease of Bob’s detection efficiency. Hence, long distances can in principle be reached if the source stays close to Alice.
