† Corresponding author. E-mail:
This paper presents calculation results for the photoassociation of a NaK molecule with a two-color modulated laser and gives a detailed analysis about them. For the two-step photoassociation process in intense fields, the effect of two-color modulated laser parameters, such as relative phase, envelope period, and laser intensity, on the population of the molecular electronic state can be obtained by solving the time-dependent Schrödinger equation through the quantum wave packet method. The numerical simulation shows not only that the influence of laser parameters on the vibrational distribution presents some regularity, but also that a higher population in the ground electronic state can be realized through adjusting these laser parameters.
Recent advances in the techniques of atomic manipulation with laser fields stimulate scientists to study the manipulation of some neutral molecules, even the cooling and trapping of polar molecules.[1] Among them, ultracold molecules have received considerable attention from researchers[2–4] due to their promising applications in such new platforms as quantum computing,[5] novel quantum phase transitions,[6] ultracold chemistry,[7–9] etc. According to the ways they are obtained through associating ultracold atoms using an external optical or magnetic field, the scheme can be classified correspondingly into two kinds, i.e., photoassociation (PA)[1,10] and magneto-association.[11,12] In particular, the formation of ultracold molecules can be achieved via PA in the long-range potential area. In the usually applied scheme, PA includes a laser-induced transition from the colliding cold atoms to a molecule in an electronic excited state. This step is followed by a transition to the molecular electronic ground state through either spontaneous or induced emission.[13] In general, the ultrashort laser pulse for PA with a broad frequency width will reduce the yield of associated molecules.
With the rapid development of laser techniques, well shaped lasers have been achieved[14,15] and widely used in the coherent PA process of the cold or ultracold molecular systems in recent years.[16] In 2006, Koch et al. investigated the PA process with chirped laser pulses in theory.[17,18] In 2008, Sugawara et al. proposed a strategy to achieve laser-field-free molecular orientation with the combination of an electrostatic field and an intense, nonresonant laser field with rapid turn-off.[19] In the same year, Salzmann et al. experimentally investigated various processes presented in the photoassociative interaction of an ultracold atomic sample with shaped femtosecond laser pulses.[20] In 2010, in order to obtain more associated molecules, Zhang et al. used a slowly-turned-on and rapidly-turned-off laser pulse to prevent the associated molecule from returning to the initial scattering state.[21] Subsequently, an efficient population accumulation in the PA process was implemented via a train of asymmetric laser pulses.[22] In the above works, the modulation of the PA process is by changing the laser parameters, which involves only the transition from a continuum state to an electronic excited state of the molecule. What we expect, however, is to produce the ultracold molecule efficiently in lower vibrational levels of the electronic ground state.
In this paper, we present a theoretical study on the formation of ultracold molecule NaK through a two-step PA process in lower vibrational levels of the electronic ground state, which is driven by a two-color modulated laser pulse. Here, we will first write out the Hamiltonian of the system in intense laser fields. Then by solving the time-dependent Schrödinger equation with time-dependent wave packet method,[23] we will obtain the wave packet evolving with time in each state. We know that the PA effect can be represented via the population of the ultracold molecule, so by analyzing the population changing with the field parameters, we can get the influence of laser parameters on the PA dynamic process.
The remainder of this paper is organized as follows: Section
In the content of the following, we mainly investigate the two-step PA process of NaK using a time-dependent wave packet method. Employing the similar method, one can study other alkali-metal atoms.[27,28]
Figure 

 | Fig. 1. (color online) The scheme of two-step PA and initial wave packet of the NaK molecule. (a) The potential energy curves and two-step PA process. (b) The norm square of the initial wave packet. |
The two-step PA process can be described by the time-dependent Schrödinger equation
 |
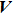
 |
 |
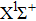
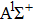
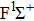
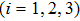
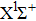
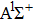
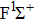
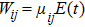
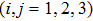

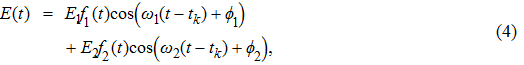 |
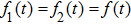
 |
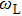
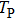
 |
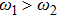
 |
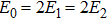
 |
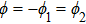
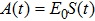
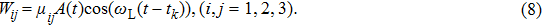 |
In the long-range region where the pump laser induces the photoassociation, the interaction of two colliding atoms at their ground states can be described by the long-range portion of the potential. So in theory here we can regard the wave function of the molecule near the dissociation limit as the initial wave function of two colliding atoms. Through solving the one-dimension time-independent Schrödinger equation by the Fourier grid Hamiltonian method,[32] the obtained initial wave packet on the electronic ground state is well represented by the wave function of the highest vibrational level 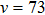

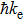
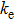
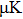
Based on the above preparations, we can write approximately the wave function using the ‘split-operator’ scheme of wave packet propagation[33,34] as follows:
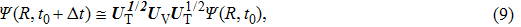 |
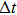
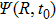
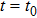
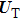
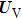
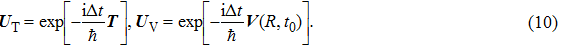 |
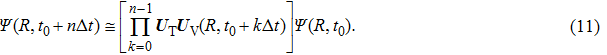 |
It is worth noting that the kinetic energy operator and the potential energy operator can be diagonalized in momentum and coordinate representations, respectively. In the propagation, when meeting the operator 
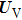
Once the wave packet at time t is obtained, the time-dependent population distribution in each state can be extracted from the norm of the wave packet 
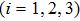
 |
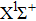
 |
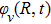
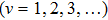
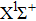
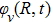
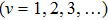
It is known that for a molecule exposed to a laser field, laser parameters, such as intensity, pulse width, delay time, and center frequency, etc., play important roles in light–matter interaction.[36] In this calculation, the relative phase ϕ, envelope period 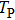


Figures 
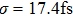
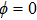
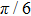

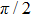


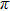

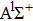
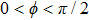

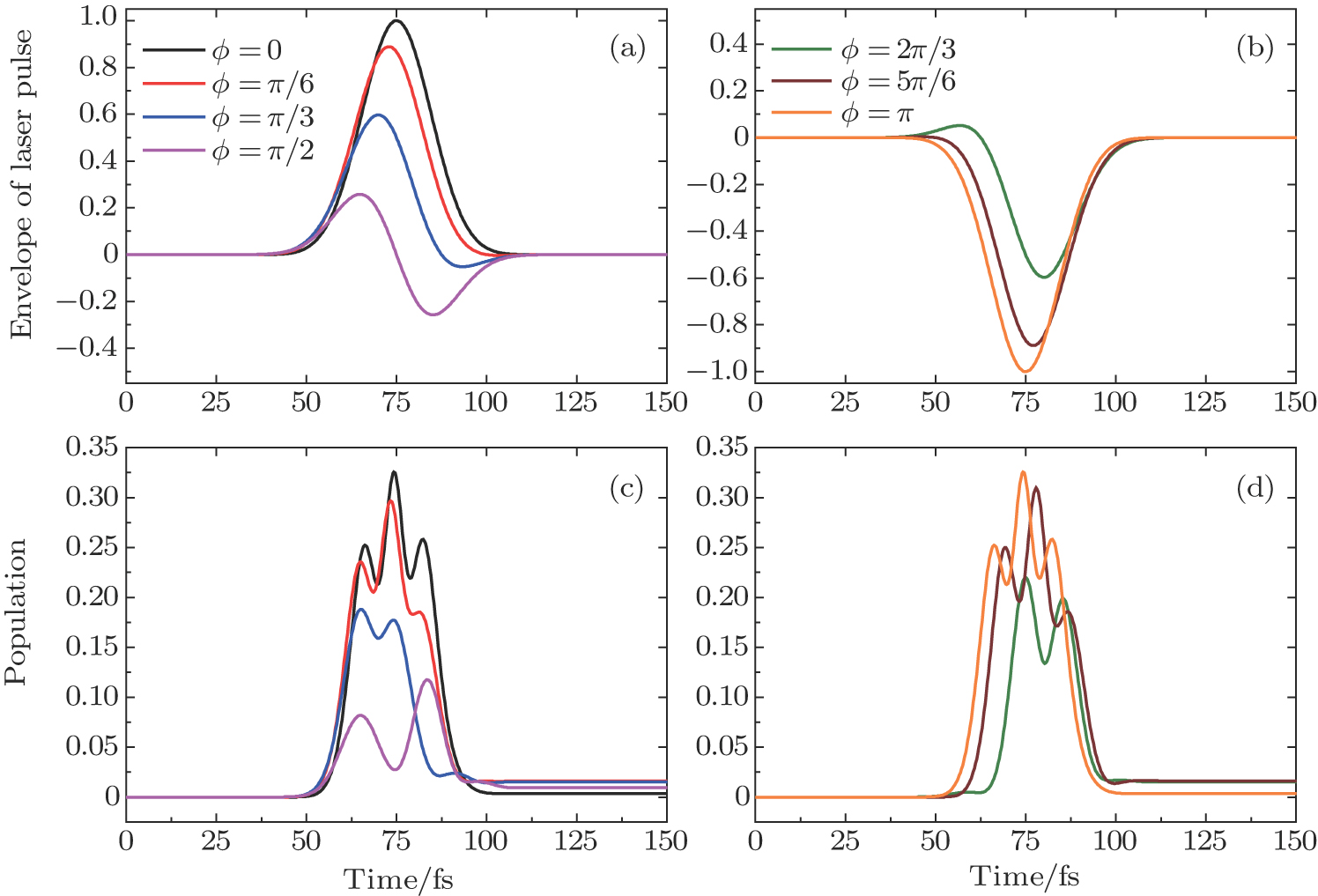 | Fig. 2. (color online) (a) and (b) the envelopes of the laser pulse with different relative phases ϕ; (c) and (d) the corresponding total population of associated molecules in 
|
Figures 




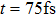

 | Fig. 3. (color online) (a) The time-dependent population in 
|
The envelope period 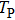
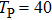


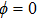

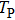
 | Fig. 4. (color online) The envelopes of the laser pulse with different periods 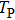

|
In order to study the influence of laser intensity on the population in 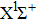



 | Fig. 5. (color online) The time evolution of the ground state (black) and the excited state (red) populations for different laser intensities: (a) 
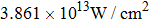


|
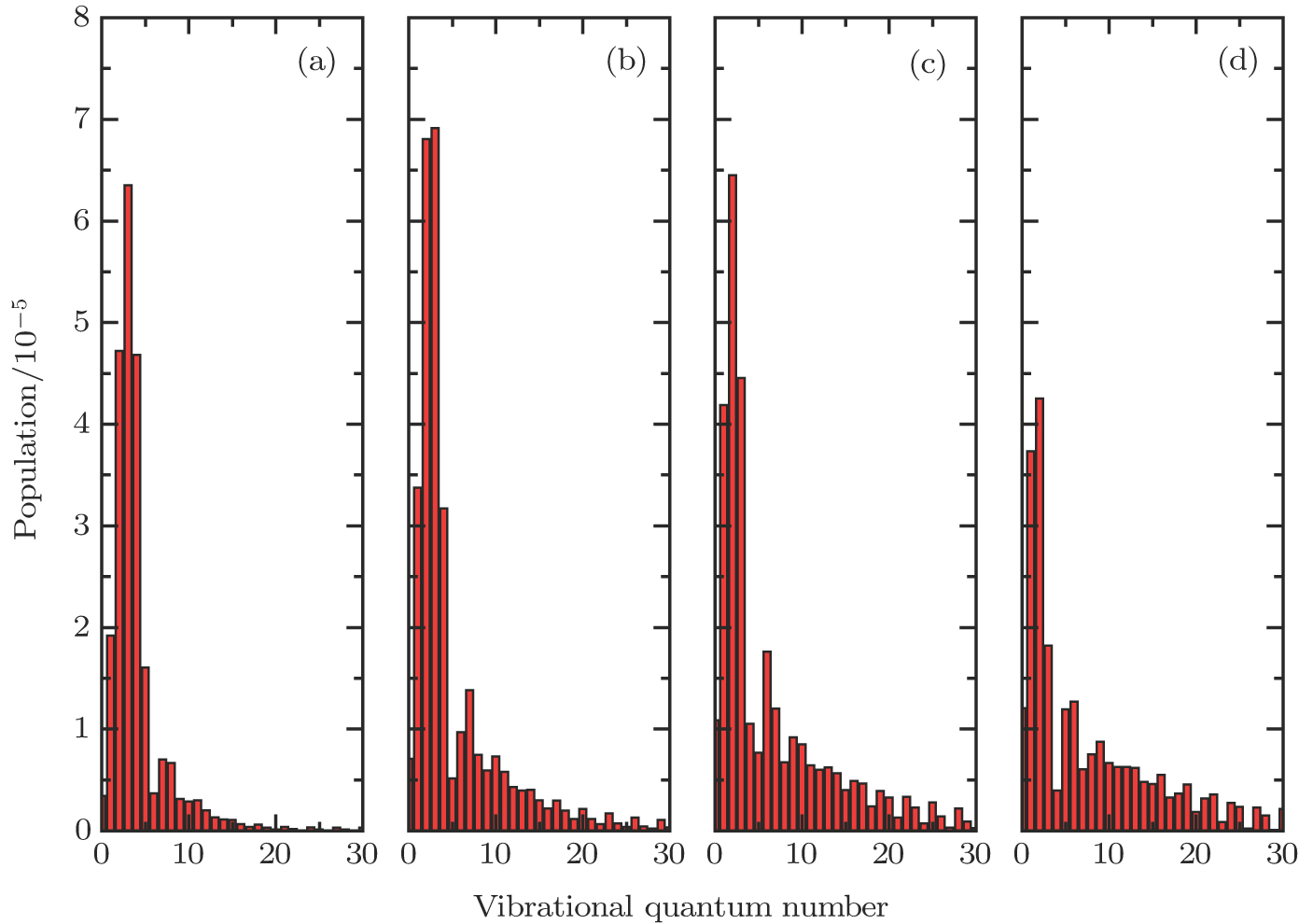
In general, the PA process tends to favor production of molecules in very high vibrational levels, and followed by a spontaneous transition back down to a ground-state continuum of hot free atoms. The phenomenon is explained by the Franck–Condon factors between the 






 | Fig. 6. (color online) FC factors between the 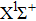

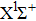
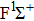
|
Through numerical calculations, we can obtain the population of each vibrational state in the electronic ground state as shown in Fig. 

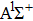

In this paper, using the time-dependent wave packet dynamical approach to investigate the two-step PA process, we derive the changing tendency of population with relative phase, envelope period and laser intensity. The results reveal that the relative phase influences the population in each electronic excited state, which reaches the maximum as 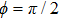
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] |