† Corresponding author. E-mail:
In this paper, the control problem of distributed parameter systems is investigated by using wireless sensor and actuator networks with the observer-based method. Firstly, a centralized observer which makes use of the measurement information provided by the fixed sensors is designed to estimate the distributed parameter systems. The mobile agents, each of which is affixed with a controller and an actuator, can provide the observer-based control for the target systems. By using Lyapunov stability arguments, the stability for the estimation error system and distributed parameter control system is proved, meanwhile a guidance scheme for each mobile actuator is provided to improve the control performance. A numerical example is finally used to demonstrate the effectiveness and the advantages of the proposed approaches.
The wireless sensor and actuator networks (WSAN) have been receiving increased research interest due to their numerous applications in the fields of cyber-physical systems, forest fire fighting, environmental and industrial monitoring, and so on.[1–3] The actuators which have much stronger power than sensors can provide the appropriate actuation on the physical systems with the help of the networked sensors. In many scenarios, mobile actuators which can be attached to the mobile agents (terrain robots, underwater vehicles, UAVs) can improve the performance in different tasks.[4–6] A series of research results have been reported in applications of static and mobile sensor and actuator networks for finite dimensional systems, such as for coverage,[4] localization,[5] and optimal control, etc.[6]
On the other hand, most of the practical systems whose states vary both spatially and temporally are infinite dimensional systems, such as many thermal, chemical processes, and fluid flow, etc. These systems are commonly termed the distributed parameter systems (DPS). The past few years have witnessed increasing interest in the distributed parameter systems.[7–13] Especially, when the wireless sensor and actuator networks are used in distributed parameter systems, the estimation or control performance of the distributed parameter systems can be effectively improved. To enhance the system performance, how to navigate the wireless sensor and actuator networks and how to choose the control architecture are the main concern to be considered. The focus for these problems has motivated recent efforts in Refs. [14]–[18] and the references therein. For example, in Ref. [15], Chao and Chen considered the sensing and distributed control of a distributed parameter system by using Centroidal Voronoi tessellations and consensus strategy in the mobile sensor and actuator networks. The static output feedback control problem and adaptive control problem for the distributed parameter systems have been studied by Demetriou in Refs. [16] and [17], respectively, meanwhile the guidance of the mobile collocated sensor and actuator networks was designed.
In practical applications, it is impossible to have all the reliable information of system states, because some state variables cannot be measured or the number of the sensors is usually finite. Hence, one needs to estimate the physical systems using the finite measurement outputs in order to provide the feedback information to controllers. Then the observer-based control method is provided to obtain certain control objectives, which is attracting many researchers.[19–21] However, to the best of our knowledge, very little research attention has been paid to the combination of the guidance design of the mobile sensor and actuator networks and the control for the distributed parameter systems using the observer-based control method. Therefore, the main purpose of this work is to shorten such a gap by the study of how to navigate the networked actuators based on the observer-based control for the distributed parameter systems.
In this article, we investigate the observer-based control for the distributed parameter systems and the guidance scheme of the wireless sensor and actuator networks. Here, it is assumed that each sensor node is fixed and each actuator node with a controller can move freely in the spatial domain. Based on the measurement information provided by the fixed sensors, a centralized observer is designed to estimate the distributed parameter control system. Then the observer-based controllers are established to control the distributed parameter systems, meanwhile a motion strategy of the mobile actuators is provided to improve the control performance by using Lyapunov stability arguments.
The rest of this paper is organized as follows. In Section
Consider the following distributed parameter system given by
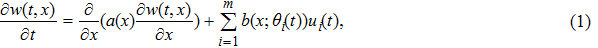 |
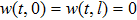
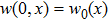
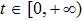

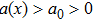
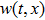
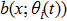
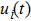
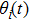
It is assumed that the spatial distributions of the m actuators are the same and given by
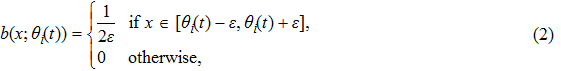 |
 |
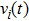
In the wireless sensor and actuator network, n distributed sensors are used to provide the following measurement outputs on the distributed parameter system (
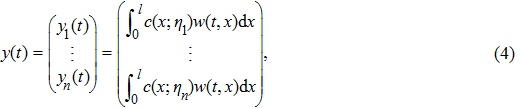 |
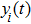
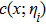
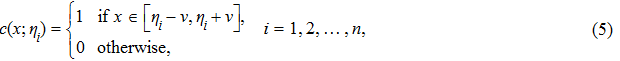 |
Based on the above measurement information by the fixed sensors, we consider the following Luenberger observer:
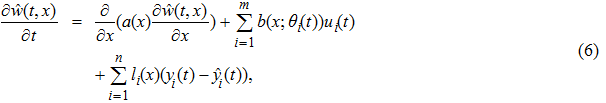 |
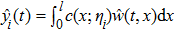 |
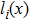
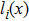
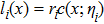
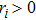
According to the Luenberger observer (
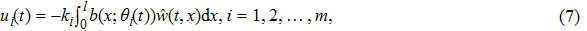 |
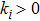
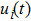
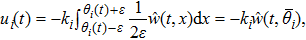 |
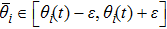

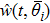
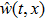
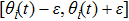
Now we can state the problem under consideration: Given the distributed parameter system (
In order to employ Lyapunov methods for the stability analysis of distributed parameter control system and the estimation error system, meanwhile to derive the guidance scheme for each mobile actuator, it is convenient to bring the above systems (
Using standard results from abstract theory, let 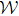
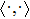
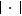
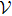
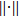
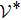
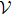

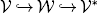
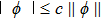
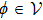
In this paper, 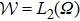
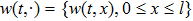
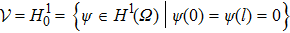
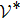
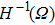
The second-order operator 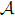
 |
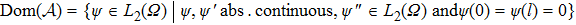
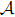
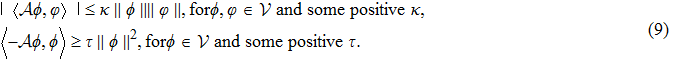 |
The input operator 
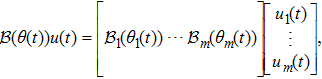 |
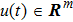

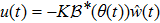

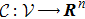
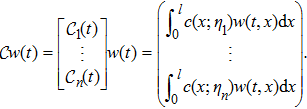 |
Then the distributed parameter control system (
 |
 |
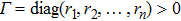
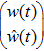
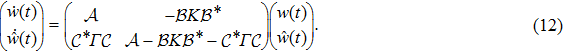 |
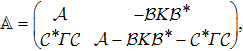 |
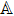
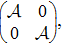 |
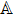
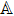
Setting 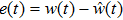
 |
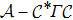
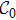
Throughout this paper, λ and μ represent the maximum eigenvalues of the bounded positive operators 
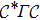

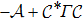
In this section, a Lyapunov-based approach will be utilized to design the trajectories of mobile actuators, meanwhile to prove the stability for distributed parameter control system (
Consider the following Lyapunov functional candidate for the systems (
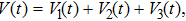 |
 |
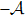
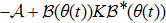
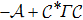
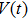
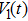
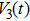
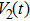
Based on the fact that the operator 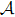

 |

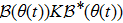
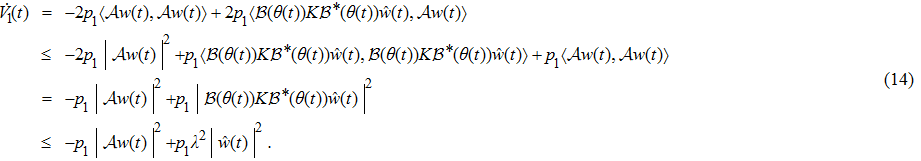 |
On the other hand, the operator 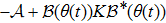
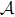
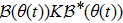
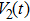
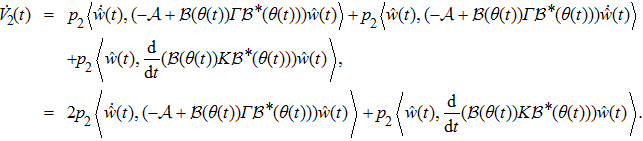 |
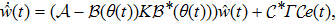 |
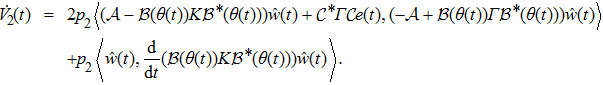 |


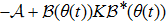
 |
Taking an examination of the last term in expression (
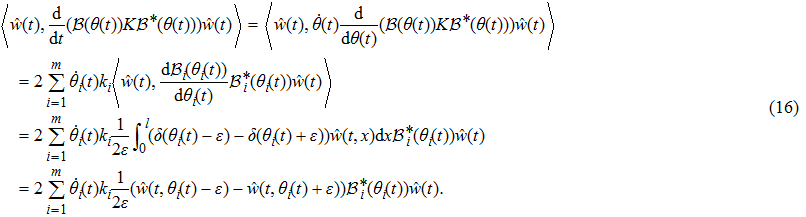 |
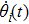
 |
 |
Noticing that the self-adjoint operator 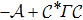
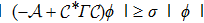
 |
Therefore, combining formulas (
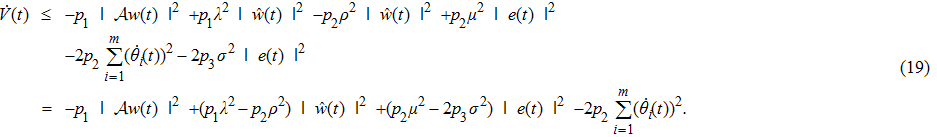 |
When the positive constants pi, 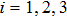
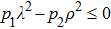
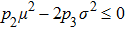
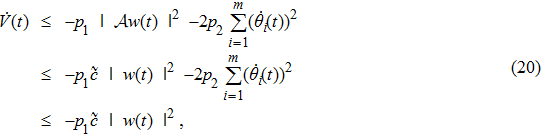 |
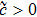
From the above analysis, the main result is now summarized in the following theorem.
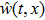
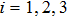
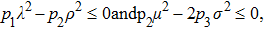 |
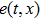
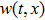
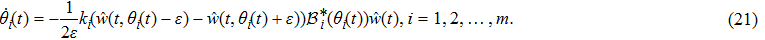 |
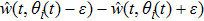
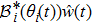
 |
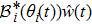
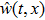
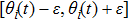
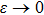
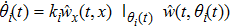

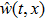
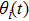
The distributed parameter system (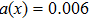
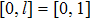
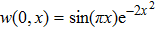
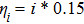
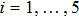

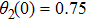

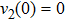
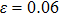
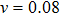
It is assumed that the centralized estimator with 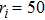
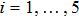
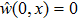
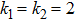
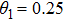
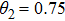
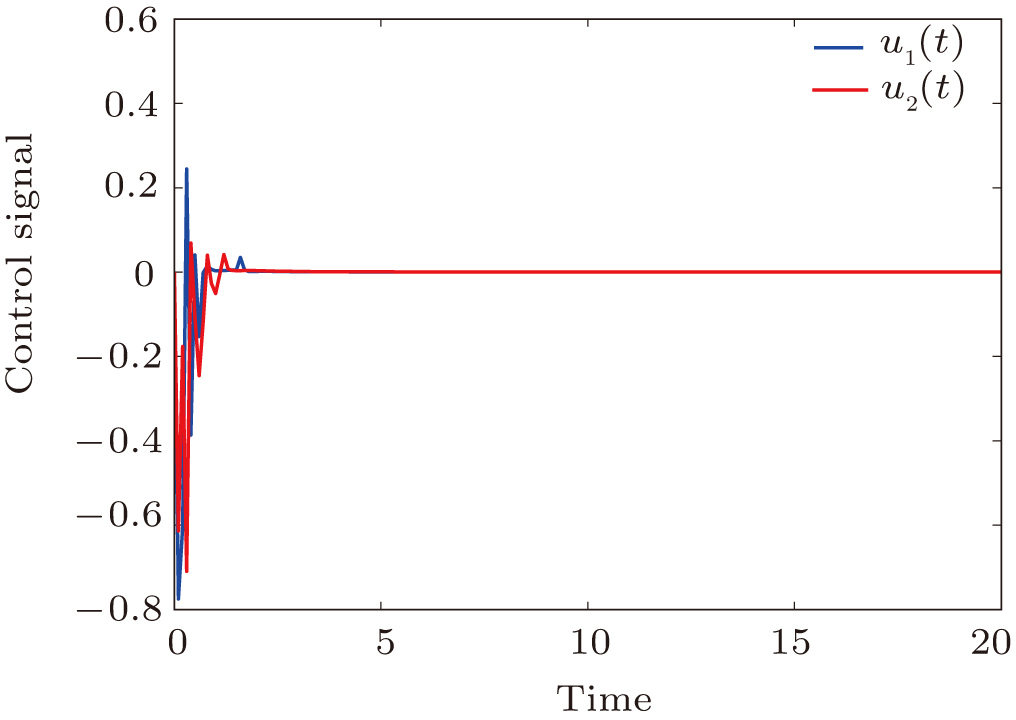
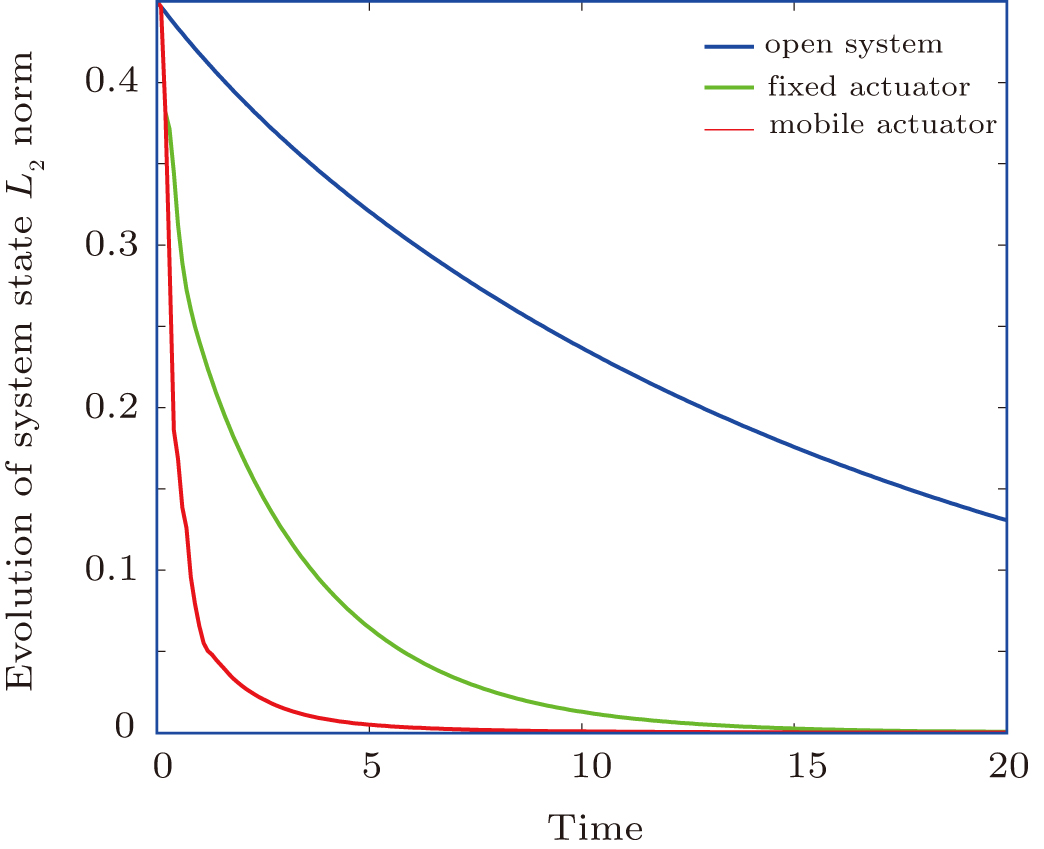
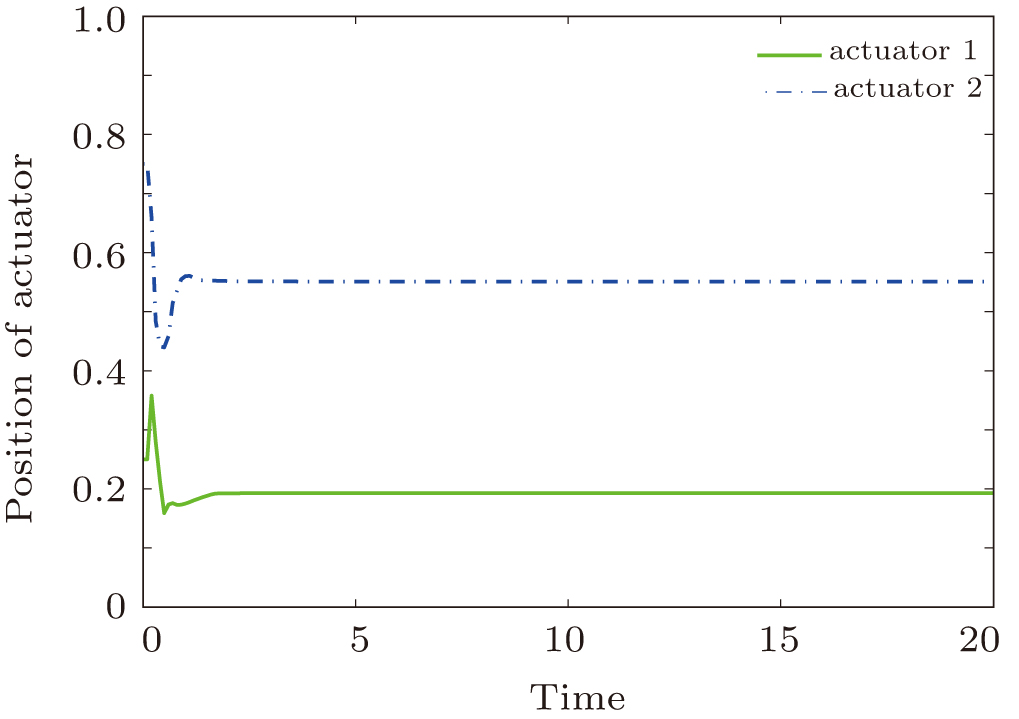
Figure
 | Fig. 1. (color online) System state and its estimate versus spatial variable at four different time instances. |
Figure 
In this paper, the observer-based control problem for the distributed parameter system has been considered by using the wireless sensor and actuator network in which it is assumed that sensors are fixed and actuators can move freely in the spatial domain. Based on the measurement information provided by the fixed sensors, a centralized observer has been designed. Meanwhile the observer-based controllers have been provided to control the distributed parameter system. Furthermore, the stability of the estimation error system and the distributed parameter control system has been analyzed by using Lyapunov stability arguments, meanwhile, a guidance scheme for each mobile actuator has been provided to improve the control performance. Simulation results have demonstrated the effectiveness and the advantages of the proposed approaches. It should be pointed out that our main result can be extended to other distributed parameter systems such as linear or nonlinear reaction–convection–diffusion systems with or without time-delays. This will be our next research work.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] |