The thermodynamic stability of the Fe_3−xMn_xAl system was evaluated by calculating the formation enthalpy and cohesive energy. In this work, in order to investigate the thermodynamic stability of the Fe_xMn_3−xAl system, the two energy formulas can be defined as

(2)

(3)

In this process, we can obtain the lattice parameters after optimizing the crystal structure. The lattice parameters, formation enthalpy, and cohesive energy of Fe, Mn, Al, and the Fe_xMn_3−xAl system are listed in Table 1. Obviously, the calculated results show good agreement with other experimental and calculated values.^[18–28] The slight deviations may result from the different calculation methods or experimental conditions. The stability of these Fe_xMn_3−xAl compounds can be estimate by the formation enthalpy and cohesive energy. In general, the lower the formation enthalpy, the better the thermodynamic stability of compounds. As can be seen from Table 1, all calculated formation enthalpy and cohesive energy are negative, which shows that these Fe_xMn_3−xAl alloys are thermal stable.

Table 1.

Table 1.

Table 1. The calculated lattice parameters (Å), cohesive energy Ecoh (eV/atom), and formation enthalpy ΔHr (eV/atom) of the Fe–Mn–Al system. . Species a = b = c Ecoh ΔHr Fe 2.78 −8.981 − 2.742a −6.07a Mn 3.54 −9.203 − Al 4.05 −3.723 − 4.0495b, 4.047h −3.39b, −3.39g − Fe3Al 11.18 −8.190 0.217 11.25c, 5.787j −4.197c, −4.183k −0.279c, −0.202k Fe2.5Mn0.5Al 11.21 −8.138 −0.199 Fe2MnAl 11.24 −8.119 −0.186 11.36d, 11.63i Fe1.5Mn1.5Al 11.29 −8.102 −0.179 FeMn2Al 11.35 −8.038 −0.158 11.52d, 11.45e Fe0.5Mn2.5Al 11.38 −7.990 −0.134 Mn3Al 11.42 −7.981 −0.127 11.61d, 11.44f a Cal. in Ref. [18]. b Cal. in Ref. [19]. c Cal. in Ref. [20]. d Cal. in Ref. [21]. e Cal. in Ref. [22]. f Cal. in Ref. [23]. g Exp. in Ref. [24]. h Exp. in Ref. [25]. i Exp. in Ref. [26]. j Exp. in Ref. [27]. k Exp. in Ref. [28].

Table 1. The calculated lattice parameters (Å), cohesive energy Ecoh (eV/atom), and formation enthalpy ΔHr (eV/atom) of the Fe–Mn–Al system. .

In Table 1, for these Fe_3−xMn_xAl alloys, the cohesive energy varies from −7.981 eV/atom to −8.190 eV/atom, and the formation enthalpy varies from −0.127 eV/atom to −0.217 eV/atom. We can find that Fe₃Al is the most stable from the point view of cohesive energy. But thermodynamic stability is decided by the formation enthalpy of the compound. Lower negative formation enthalpy implies much more stable crystal structure. Figure 2 shows the calculated cohesive energy and formation enthalpy with Mn-content change curves. We can see that the cohesive energy and formation enthalpy increase with Mn atom content increasing. Comparing these formation enthalpies, we can find that the formation enthalpy of Fe₃Al is the lowest. Therefore, we believe that Fe₃Al is the most stable in the Fe_3−xMn_xAl system.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (color online) Variations of cohesive energy and formation enthalpy of Fe3−xMnxAl system.

In this section, in order to analyze the chemical bonding characteristics and electronic structures of the Fe_3−xMn_xAl system, we report our calculations of the total density of states (TDOS), partial density of states (PDOS), and electron density distribution maps. The calculated electronic structures are shown in Figs. 3 and 4.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (color online) Calculated total density of states and partial density of states for Fe and Fe3−xMnxAl system. Dashed lines represent the Fermi level.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (color online) (a), (c), (e), (g), (i), (k), (m) Total electron density distribution contours and (b), (d), (f), (h), (j), (l), (n) electron density difference distribution contours for Fe3−xMnxAl system.

The calculated partial density of states and total density of states of the Fe_3−xMn_xAl system are shown in Fig. 3. All of these Fe–Mn–Al alloys have metallic features because the density of states is non-zero at the Fermi level. The nature of the magnetic characteristics can be understood from the spinpolarized total density of states. Generally speaking, the down and up states are almost symmetric, but comparing the down and up states, we can find that these alloys have magnetic characteristics that are due to the dissymmetry of the down and up states. Fe and Mn are transition metals, for which we need to consider only the role of the outermost electrons. Through the states density of Fe, we can find that it is affected by the Fe-d bands primarily. From Fig. 3, we can find that near the Fermi level in the Fe–Mn–Al alloys, the up and down density of states curves are divided mainly into three sharp peaks. These peaks are primarily determined by the Fe-d and Mn-d states. For Fe₃Al, the band range from −5 eV to 3 eV is contributed mainly by the Al-p bands and Fe-d bands. For Mn₃Al, the band range from −5 eV to 3 eV is decided mainly by the Al-p bands and Mn-d bands. For other Fe–Mn–Al alloys, the band range from −5 eV to 3 eV is determined mainly by the Al-p bands, Fe-d bands, and Mn-d bands. Near the Fermi level, the TDOS of Fe₃Al and Mn₃Al are composed mainly of the small Al-d states hybridized with the Fe-d states and Mn-d states, respectively. The TDOS of the other Fe–Mn–Al alloys mainly shows hybridization among the small Al-d states, Fe-d states, and Mn-d states. Additionally, the curves of the PDOS of the Fe₃Al and Mn₃Al indicate that the Fermi surface is primarily from the contribution of Fe-d states and Mn-d states, respectively, but they also involve small Al-p states. The curves of PDOS of the other Fe–Mn–Al alloys show that the Fermi surface is primarily from the contribution of Fe-d states and Mn-d states, but also involves small Al-p states. From what has been discussed above, we may safely draw the conclusion that the bonding features of the Fe_3−xMn_xAl system are combinations of covalent bonds and metallic bonds, which may lead to good electronic conductivity, relatively high melting points, and hardness.

The calculated total electron density distribution maps and electron density difference distribution maps of the Fe_3−xMn_xAl system are shown in Fig. 4. From Figs. 4(a), 4(c), 4(e), 4(g), 4(i), 4(k), and 4(m), we can see that all the Fe, Mn, and Al of core regions have smaller interstitial areas and larger values. Through these pictures, we can see the Fe, Mn, and Al atoms’ covalent bonds features clearly. From these total electron density distribution maps, we can find that the elongated contours along the Al–Fe, Al–Mn, and Fe–Mn bond axes indicate existing covalent interactions. More details about chemical bonding characteristics can be found from the electron density difference distribution in Figs. 4(b), 4(d), 4(f), 4(h), 4(j), 4(l), and 4(n). Some electrons are delocalized and distributed through the circular map in the area among Al, Mn, and Fe atoms, which collectively implies the features of covalent bonding and metallic bonding. The electron areas are actually situated around the Mn, Fe, and Al atoms in the blue color, which indicates that covalent bonds exist between Mn, Fe, and Al atoms. Fe₂MnAl, Fe_2.5Mn_0.5Al, and FeAl₃ alloys have the covalent bonding behavior among the Al and Fe atoms, Mn₃Al has the covalent bonding behavior among the Al and Mn atoms, Fe_0.5Mn_2.5Al, FeMn₂Al, and Fe_1.5Mn_1.5Al alloys have the covalent bonding behavior among the Al, Fe, and Mn atoms. Fe₂MnAl and Fe_2.5Mn_0.5Al alloys have the metallic bonding behavior among the Fe atoms. FeMn₂Al and Fe_1.5Mn_1.5Al alloys have the metallic bonding behavior among the Fe and Mn atoms. Fe_0.5Mn_2.5Al alloys have the metallic bonding behavior among the Mn atoms. Also we can see that the Fe–Mn–Al system exhibits anti-bond effect, such as the Fe–Al anti-bond of Fe₃Al, Mn–Al anti-bond of Mn₃Al. Other alloys also exhibit Mn–Fe or Al–Mn anti-bond, and so on.

According to the above discussion, these Fe–Mn–Al alloys have magnetic characteristics. The bonding characteristics of these Fe–Mn–Al alloys are combinations of covalent bonds and metallic bonds, also exhibiting an anti-bond effect. The interaction between Fe and Al is mainly covalent bonds. Based on the Fe (1.83), Mn (1.55), and Al (1.61) electronegativity, the electronegativity difference is small, so their covalent interactions are weak. We can conclude that these alloys have weaker covalent bonding effects. These bonding features may lead to relatively high melting points and hardness.

The Fe–Mn–Al alloys are potentially high-strength materials, so investigation of mechanical performance is very important. We calculated the elastic constants of the Fe_3−xMn_xAl system. The results are listed in Table 2. There are three independent elastic constants (C₁₁, C₁₂, and C₄₄) of the Fe_3−xMn_xAl alloys. From the angle of mechanical properties, we further investigated the stability of the Fe_3−xMn_xAl system. Here, we discuss the formulas of mechanical stability criteria by the elastic moduli of crystal structure. The mechanical stability conditions can be defined as follows for the cubic system:^[29]

Table 2.

Table 2.

Table 2. Calculated elastic constants (Cij), bulk modulus, shear modulus, Young’s modulus, hardness, B/G, and Poisson’s ratio (σ) of Fe–Mn–Al alloys; the units are GPa. . Species C11 C12 C44 B G E σ HV B/G Fe3Al 284.7 207.5 151.0 233.2 87.9 234.3 0.333 5.76 2.65 283.48 a 205.63 a 149.08 a 231.5 a 87.5 a 0.4 a 2.65 a 171.0 g 130.6 g 131.7 g 144.1 g Fe2.5Mn0.5Al 295.8 203.3 141.6 234.5 91.1 241.9 0.328 6.27 2.57 Fe0.5Mn0.1Al0.4 164.1 e 97.4 e 127.4 e 119.6 e 75.0 e 186.1 e 0.241 e 1.60 e Fe2MnAl 301.7 198.5 133.9 233.2 91.5 242.8 0.326 6.40 2.55 214.1 b 70.3 b 168.4 b 118.2 b 119.7 b 268.6 b 0.12 b 200.9 c 210.1 d Fe2TiAl 288.6 b 137.4 b 105.9 b 187.8 b 92.5 b 238.5 b 0.29 b 2.03 b Fe2CrAl 289.7 a 153.0 a 156.7 a 201.0 a 108.3 a 0.35 a 1.85 a Fe1.5Mn1.5Al 318.9 184.4 128.1 229.5 98.8 259.2 0.312 7.96 2.32 180.8 c FeMn2Al 296.5 192.4 129.9 227.1 88.4 234.7 0.328 6.13 2.57 150.2 c Fe0.5Mn2.5Al 267.9 201.7 129.5 223.8 75.5 203.6 0.348 4.04 2.96 150.7 c Mn3Al 297.2 189.0 124.4 225.0 89.1 236.1 0.325 6.35 2.53 143.9 c Ni3Al 243.8 f 148.7 f 123.4 f 180.4 f 84.2 f 218.5 f 2.14 f a Cal. in Ref. [32]. b Cal. in Ref. [33]. c Cal. in Ref. [21]. d Cal. in Ref. [34]. e Cal. in Ref. [7]. f Cal. in Ref. [35]. g Exp. in Ref. [36].

Table 2. Calculated elastic constants (Cij), bulk modulus, shear modulus, Young’s modulus, hardness, B/G, and Poisson’s ratio (σ) of Fe–Mn–Al alloys; the units are GPa. .

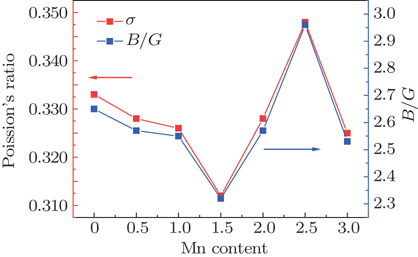
From Table 2, we can clearly find that these Fe–Mn–Al alloys are mechanically stable, because the above criteria are satisfied. After the elastic constants are obtained, the bulk modulus (B), Poisson’s ratio (σ), Young’s modulus (E), and shear modulus (G) of polycrystalline crystal can be obtained by the Voigt–Reuss–Hill (VRH) approximation^[30,31]

Here, the subscripts R and V indicate the Reuss and Voigt averages. B_VRH, B_V, andB_R are the bulk moduli calculated by Voigt–Reuss–Hill, Voigt, and Reuss approximation methods, respectively. G_VRH, G_V, and G_R are the shear moduli calculated within Voigt–Reuss–Hill, Voigt, and Reuss approximation methods, respectively.

The results of calculations and experiments are listed in Table 2, and our calculated results are in good agreement with the literature.^{[7,21,32–36]} The slight deviations may come from the different calculation methods and experimental conditions. As seen from Table 2, Fe_1.5Mn_1.5Al has the largest C₁₁, 318.9 GPa, which shows that Fe_1.5Mn_1.5Al is highly incompressible under uniaxial stress along the crystallographic x axis (ε₁₁). C₄₄ represents the shear modulus on the (100) crystal planes. As seen from Table 2, Mn₃Al has the smallest C₄₄ and Fe₃Al has the largest C₄₄ in the Fe_3−xMn_xAl system, with values of 124.4 GPa and 151.0 GPa, respectively. The bulk modulus B, shear modulus G, Poisson’s ratio σ, and Young’s modulus E were calculated using Eqs. (5)– (10) and are listed in Table 3. As we know, the bulk modulus reflects the compressibility of the solid under hydrostatic pressure. In the Fe_3−xMn_xAl system, the bulk moduli are 233.2 GPa, 234.5 GPa, 233.2 GPa, 229.5 GPa, 227.1 GPa, 223.8 GPa, and 225.0 GPa for Fe₃Al, Fe_2.5Mn_0.5Al, Fe₂MnAl, Fe_1.5Mn_1.5Al, FeMn₂Al, Fe_0.5Mn_2.5Al, and Mn₃Al, respectively. The shear modulus is resistance to deformations upon shear stress, and the values are 87.9 GPa, 91.1 GPa, 91.5 GPa, 98.8 GPa, 88.4 GPa, 75.5 GPa, and 89.1 GPa for Fe₃Al, Fe_2.5Mn_0.5Al, Fe₂MnAl, Fe_1.5Mn_1.5Al, FeMn₂Al, Fe_0.5Mn_2.5Al, and Mn₃Al, respectively. Generally speaking, the greater the shear modulus, the higher the hardness of the compound. Young’s modulus offers a ruler of the stiffness of solid materials. The greater Young’s modulus is, the larger the stiffness of the materials is. As seen from Table 2, Fe_1.5Mn_1.5Al has the largest Young’s modulus and shear modulus with values of 259.2 GPa and 98.8 GPa, respectively, which indicates that Fe_1.5Mn_1.5Al may have the largest hardness in the Fe_3−xMn_xAl system. Poisson’s ratio can reflect the stability of the crystal against shear stress. In this work, we calculated Poisson’s ratios of the Fe_3−xMn_xAl system and the values range from 0.312 to 0.348. If Poisson’s ratio is close to 0.3, the compound has strong metallic bonding features. Otherwise, Poisson’s ratios deviate from 0.3, which shows that these alloys have covalent bonding. The value of B/G is usually applied to indicate a compound’s brittleness or ductility.^[37] The material has the ductile characteristics when B/G ratio is greater than 1.75; otherwise, the material is brittle. In this work, the values clearly imply that all Fe–Mn–Al alloys are ductile. The Vickers hardness (H_V) of the Fe_3−xMn_xAl system is forecast by an empirical model that gives better results for anisotropic structures. The calculation formula is^[38]

(11)

Table 3.

Table 3.

Table 3. Calculated universal anisotropic index (AU), anisotropy (AB and AG), and shear anisotropic factors (A1, A2, A3) of Fe–Mn–Al alloys. . Species AU AB AG A1 = A2 = A3 Fe3Al 2.59 0 0.205 3.91 Fe2.5Mn0.5Al 1.68 0 0.144 3.12 Fe2MnAl 1.23 0 0.110 2.59 Fe1.5Mn1.5Al 0.51 0 0.049 1.90 FeMn2Al 1.15 0 0.103 2.50 Fe0.5Mn2.5Al 2.58 0 0.205 3.90 Mn3Al 0.88 0 0.081 2.30

Table 3. Calculated universal anisotropic index (AU), anisotropy (AB and AG), and shear anisotropic factors (A1, A2, A3) of Fe–Mn–Al alloys. .

In order to further depict the mechanical properties of the Fe_3−xMn_xAl system, some elastic moduli with change to Mn atom content are curve listed in Figs. 5–7. From Fig. 5, we can find that the Young’s modulus and C₁₁ −C₁₂ have similar variation tendencies. As can be seen from Fig. 6, the bulk modulus and C₄₄ have similar variation tendencies, but the relationship among shear modulus, bulk modulus, and C₄₄ cannot be observed clearly. From Fig. 7, we can see that Poisson’s ratio and B/G have the same change trend.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. (color online) Variations of the C11 – C12 and Young’s modulus of Fe3–xMnxAl system.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. (color online) Variations of the bulk modulus, shear modulus, and C44 of Fe3−xMnxAl system. Note that the shear modulus is magnified by 2 times.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. (color online) Variations of Poisson’s ratio and B/G of Fe3−xMnxAl system.

All of the single crystals are actually anisotropic, therefore, a suitable parameter describing the anisotropic degree is necessary. Meanwhile, the appearance of micro cracks in materials is always connected with the anisotropy. The micro cracks often form in materials and harm the performance of the materials. Fe–Mn–Al alloys are potential high-strength materials, so the anisotropic mechanical properties of these alloys are investigated carefully. We calculated several anisotropic indexes, including the anisotropy index (A_B and A_G), the shear anisotropic factors (A₁, A₂, and A₃), and universal anisotropic index (A^U). The equations are as follows:^[39]

(12)

(13)

(14)

(15)

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. (color online) Variations of the AG and AU of Fe3−xMnxAl system.

In order to better depict the features of elastic anisotropy, we plotted a curved surface of three dimensions (3D). In this work, the Young’s modulus is plotted at different directions using spherical coordinates. And the directional dependence of Young’s modulus can be given by the following equations for cubic crystal:^[40]

Here, l₁, l₂, and l₃ are the directional cosines, and S_ij are the elastic compliance constants. In the spherical coordinates, l₁ = sin[θ]cos[ψ], l₂ = sin[θ]sin[ψ], and l₃ = cos[θ]. The angle between θ and ψ is defined on the horn in the spherical coordinates. The 3D curved surface of the Young’s modulus of the Fe_3−xMn_xAl system is shown in Fig. 9. These graphs represent the size of Young’s modulus along different directions. Obviously, figure 9 shows that these Fe–Mn–Al alloys have a strong anisotropy feature in Young’s modulus. Meanwhile, we can clearly see that these alloys have similar anisotropies; Fe₃Al has the strongest anisotropy of Young’s modulus, while Fe_1.5Mn_1.5Al has the weakest. More details of the anisotropic properties of Young’s modulus on the (001) and (110) planes are illustrated in Fig. 10. On these planes, we can clearly see that the Young’s modulus has a strong directional dependence. At the [100], [010], [001], and [110] directions, we can find that Fe_1.5Mn_1.5Al shows the maximum Young’s modulus, while Fe_0.5Mn_2.5Al shows the minimum Young’s modulus. For these alloys, the planar contours on the (001) and (110) planes are not similar to a spherical shape, which indicates that the Young’s modulus of these alloys shows strong anisotropy on the (001) and (110) planes.

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. (color online) Contour plots of the Young’s modulus of the Fe3−xMnxAl system in 3D space.

Fig. 10.

	Figure Option ViewDownloadNew Window
	Fig. 10. (color online) Planar projections of the Young’s modulus of the Fe3−xMnxAl system on the (a) (001) and (b) (110) crystallographic planes.

The sound velocities of transverse and longitudinal modes of the Fe_3−xMn_xAl system are calculated using the single crystal elastic constants.^[41] The sound velocities are determined by the propagation direction and symmetry of the crystal. The pure longitudinal and transverse modes are found in [100], [110], and [001] directions, and the sound propagating modes in other directions are the quasi-longitudinal or quasi-transverse waves. In the principle directions, the acoustic velocities can be calculated using the following relations:^[42–44]

Here, v_l is the longitudinal sound velocity; v_t1 is the first transverse modes; v_t2 is the second transverse modes; and ρ is the theoretical density. The calculated anisotropic sound velocities of the Fe_3−xMn_xAl alloys are listed in Table 4. Obviously, these alloys have large elastic moduli and smaller densities, leading to fast sound velocities.

Table 4.

Table 4.

Table 4. Anisotropic sound velocities of Fe–Mn–Al alloys; the unit of velocity is m·s−1. . Species [100] [110] [001] vl vt1 vt2 vl vt1 vt2 vl vt1 vt2 Fe3Al 6198.2 4514.0 4514.0 7320.2 3227.6 4514.0 7657.7 3203.8 3203.8 Fe2.5Mn0.5Al 6354.5 4396.6 4396.6 7307.2 3553.5 4396.6 7598.3 3263.8 3263.8 Fe2MnAl 6456.3 4301.2 4301.2 7283.9 3776.1 4301.2 7539.6 3304.5 3304.5 Fe1.5Mn1.5Al 6691.5 4241.0 4241.0 7302.1 4345.7 4241.0 7494.5 3505.8 3505.8 FeMn2Al 6502.1 4303.7 4303.7 7306.0 3852.7 4303.7 7555.0 3334.9 3334.9 Fe0.5Mn2.5Al 6223.0 4326.6 4326.6 7256.8 3093.5 4326.6 7570.1 3070.8 3070.8 Mn3Al 6586.8 4261.5 4261.5 7324.5 3974.3 4261.5 7554.4 3364.3 3364.3

Table 4. Anisotropic sound velocities of Fe–Mn–Al alloys; the unit of velocity is m·s−1. .

The Debye temperature is a fundamental parameter and is related to some physical properties of materials, such as specific heat, elastic constants, and melting point.^[45] It is obvious that the Debye temperature and sound velocity can be used to estimate the chemical thermal properties and chemical bond behavior of compounds. The average sound velocity (v_m) and Debye temperature (Θ_D) can be calculated using the following equations:^[46]

(18)

(19)

(20)

(21)

We calculated the sound velocities and Debye temperature of the Fe_3−xMn_xAl system, and the values are listed in Table 5. In general, the Debye temperature can help understand the thermal properties and chemical bonding features of a compound. For crystal structure, the Debye temperature can reflect the strength of covalent bonding. From Table 5, we can find that Fe_1.5Mn_1.5Al has the largest Θ_D, with the value of 551.1 K. So we conclude that Fe_1.5Mn_1.5Al has stronger covalent bonds than other Fe_xMn_3−xAl alloys. Fe_0.5Mn_2.5Al has the highest B/G ratio and lowest Θ_D, at 487.2 K, which shows the strongest metallic character. More details can be found from Fig. 11. Obviously, the Debye temperature increases from Fe₃Al to Fe_1.5Mn_1.5Al with the increases of Mn content, but the Debye temperature decreases from Fe_1.5Mn_1.5Al to Fe_0.5Mn_2.5Al. The hardness and Debye temperature have the same change trend, maybe because the bonding features of these alloys have the same trend effects for hardness and Debye temperature. In addition, the calculated average sound velocities of the Fe_3−xMn_xAl system are relatively large, because they have large elastic moduli and smaller densities, and the v₁ and v_s values are concerned with density, shear modulus, and bulk modulus.

Table 5.

Table 5.

Table 5. Theoretical density (ρ, kg·m−3), longitudinal sound velocity (vl, m·s−1), transverse sound velocity (vs, m·s−1), average sound velocity (vm, m·s−1), and Debye temperature (ΘD, K). . Species ρ v1 vs vm ΘD Fe3Al 7.41 6876.3 3444.0 3863.2 516.6 Fe2.5Mn0.5Al 7.33 6970.9 3526.5 3953.3 527.0 Fe2MnAl 7.24 7054.2 3555.6 3985.1 529.6 Fe1.5Mn1.5Al 7.12 7121.8 3724.6 4166.5 551.1 FeMn2Al 7.01 7013.4 3550.3 3979.8 524.2 Fe0.5Mn2.5Al 6.92 6848.6 3303.6 3713.5 487.2 Mn3Al 6.85 7084.4 3606.5 4041.4 528.9

Table 5. Theoretical density (ρ, kg·m−3), longitudinal sound velocity (vl, m·s−1), transverse sound velocity (vs, m·s−1), average sound velocity (vm, m·s−1), and Debye temperature (ΘD, K). .

Fig. 11.

	Figure Option ViewDownloadNew Window
	Fig. 11. (color online) Variations of the hardness and Debye temperature of the Fe3−xMnxAl system.