Cite this Article
Liu Heng, Li Sheng-Gang, Wang Hong-Xing, Li Guan-Jun. Adaptive fuzzy synchronization for a class of fractional-order neural networks. Chinese Physics B, 2017, 26(3): 030504  
Permissions
Adaptive fuzzy synchronization for a class of fractional-order neural networks
Liu Heng1, 2, Li Sheng-Gang1, †, Wang Hong-Xing2, Li Guan-Jun2
College of Mathematics and Information Science, Shaanxi Normal Universtiy, Xi’an 710119, China
Department of Applied Mathematics, Huainan Normal University, Huainan 232038, China

 

† Corresponding author. E-mail: shengganglinew@126.com

Abstract

In this paper, synchronization for a class of uncertain fractional-order neural networks with external disturbances is discussed by means of adaptive fuzzy control. Fuzzy logic systems, whose inputs are chosen as synchronization errors, are employed to approximate the unknown nonlinear functions. Based on the fractional Lyapunov stability criterion, an adaptive fuzzy synchronization controller is designed, and the stability of the closed-loop system, the convergence of the synchronization error, as well as the boundedness of all signals involved can be guaranteed. To update the fuzzy parameters, fractional-order adaptations laws are proposed. Just like the stability analysis in integer-order systems, a quadratic Lyapunov function is used in this paper. Finally, simulation examples are given to show the effectiveness of the proposed method.

PACS: 05.45.Gg
Keyword:fractional-order neural network;adaptive fuzzy control;fractional-order adaptation law
1. Introduction

Fractional calculus is a concept for the theory of integrals and derivatives of arbitrary order, which unifies and generalizes the notions of integer-order differentiation and n-fold integration.[1] This idea is around 300 years old, but compared with the corresponding integer-order theory, the developments in this field have been rather slow. But lately, there has been a steady growth of interest in this field because lots of actual systems show fractional-order differential dynamical behaviors.[2–8] Applications of fractional-order differential equations to different areas are investigated by many researchers, and some basic results have been obtained (see, for example, Refs. [2], [3], [6], [7], and [9] and the references therein). One can refer to Refs. [1] and [10] for more details about the fractional calculus theory. In a manner of speaking, dynamics analysis, stability analysis, and the control of fractional-order systems have become very hot and promising research topics.

One main advantage of fractional-order systems consists in that the fractional-order differential operator takes into consideration the fact that the future system states depend on both the present states and all the previous states. That is to say, the fractional-order systems are nonlocal while the integer-order ones are local. Noting that fractional calculus provides a powerful tool for describing memory and hereditary properties of the systems, some researchers have put it into integer-order neural networks to achieve fractional-order neural models, which may better describe the dynamical behavior of the neurons.[2,11–18] Up to now, various significant issues about fractional-order neural networks have been discussed. In Ref. [19], by using numerical simulations, the complex dynamics of a class of fractional-order neural networks have been addressed. In Ref. [20], the dynamics of a general class of fractional-order neural networks were investigated by means of the Krasnoselskii fixed point theorem and the contraction mapping principle. In Refs. [12] and [13], based on the Lyapunov stability criterion and linear control strategies, some effective criteria concerning stability analysis of fractional-order neural networks and memristor-based fractional-order neural networks were proposed, respectively. Besides, more and more researchers have focused on the synchronization of fractional-order neural networks, and many results have been reported (see, Refs. [13]–[18] and [21]–[27]). It should be stressed that in the aforementioned literatures considering the synchronization of fractional-order neural networks, prior knowledge of the system models is needed. However, as we know, system uncertainties and external disturbances usually exist in actual systems,[28–34] so it is advisable to design a synchronization controller for fractional-order neural networks when the system models are fully unknown.

It is well known that fuzzy systems with linguistic information or heuristic knowledge have been successfully used to control uncertain systems because the accurate mathematical models of the systems are not needed.[34–43] Based on the universal approximation theorem,[44] many adaptive fuzzy control methods have been developed for uncertain integer-order nonlinear systems.[35,36,45–49] However, with respect to fractional-order systems, one can hardly check the stability of the systems by looking for the dominant roots or via algebraic methods, which are usually utilized to analyze the stability of integer-order systems. That is to say, most of the control methods for integer-order systems cannot be extended to fractional-order systems directly. To the best of our knowledge, synchronization of fractional-order neural networks by using adaptive fuzzy control is rarely reported and needs to be investigated further.

Motivated by the above discussion, we will investigate the synchronization problem of a class of fractional-order neural networks. Roughly stated, the main contributions of this paper can be summarized as follows.

Synchronization for a class of fractional-order neural networks with fully unknown system models is discussed by using adaptive fuzzy control.

The fuzzy logic systems use synchronization errors instead of system states as their inputs. Thus, the control systems will be more sensitive to the synchronization errors.

Fractional-order adaptations laws are designed to update the fuzzy system parameters online.

The remainder of this paper is organized as follows. Section 2 introduces the fuzzy logic systems and lists some preliminaries. In Section 3, an adaptive fuzzy synchronization controller is designed and the stability of the closed-loop system is discussed by using fractional Lyapunov stability criterion. Simulation studies are presented in Section 4. Finally, Section 5 gives the conclusion of this work.

2. Preliminaries
2.1. Some basic results of fractional calculus

The fractional-order integro-differential operator can be seen as an extended concept of the integer-order one. The commonly used definitions in the literature are Grünwald–Letnikov, Riemann–Liouville, and Caputo definitions. The main reason why Caputo’s derivative is introduced for engineering applications is that its Laplace transform only requires integer-order derivatives for the initial conditions. On the contrary, the classical Riemann–Liouville definition needs fractional-order initial conditions which are difficult to be physically interpreted. We will use the Caputo derivative in this paper. The fractional-order integral with fractional order α can be defined as

(1)
where Γ represents the Euler Gamma function. The Caputo fractional derivative is expressed by
(2)
where α is the fractional order, and n is an integer satisfying n − 1 ≤ α < n.

The Laplace transform of the Caputo fractional derivative is

(3)
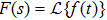
where F(s) is the Laplace transform of f(t), . For convenience, we always assume α ∈ (0, 1) in the rest of this paper. The following definitions and results are needed.

2.2. Description of a fuzzy system

A fuzzy logic system consists of four parts:[35,36,38–40,51] the knowledge base, the fuzzifier, the fuzzy inference engine working on the fuzzy rules, and the defuzzifier. The structure of a fuzzy logic system is shown in Fig. 1.

Fig. 1. (color online) The structure of a fuzzy logic system.

Usually, a fuzzy logic system is modeled by

(19)
where (a Lipschitz continuous mapping from a compact subset to the real line ) is called the output of the fuzzy logic system, (the set of all continuous mappings from to which have continuous derivatives) is called the input vector, , is consisted of fuzzy sets , (a mapping from to the closed unit interval ) is called the membership function of rule (here rules defined as follows are also need to approximate the unknown function ( ): rule j : if is , then is ), and (a mapping from to ) is called the centroid of the j-th consequent set ( ); we may identify J with for the sake of convenience. Write and , where (called the j-th fuzzy basis function, ) is a continuous mapping (and thus is continuous) defined by
Then system (19) can be rewritten as
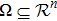
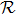
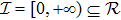
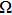
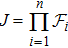
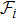
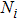
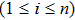
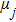
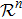
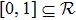
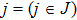
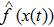
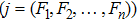
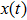
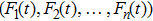
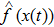
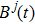
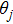
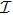
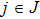
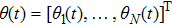
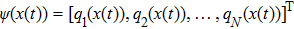
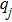
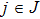
(20)

In contrast to the conventional control techniques, fuzzy logic systems are best utilized in complex ill-defined processes that can be controlled by a skilled human operator without much knowledge of their underlying dynamics. The basic idea behind fuzzy logic systems is to incorporate the “expert experience” of a human operator in the design of the controller in controlling a process whose input–output relationship is described by a collection of fuzzy control rules involving linguistic variables rather than a complicated dynamic model.

3. Adaptive fuzzy synchronization controller design and stability analysis
3.1. Problem statement

In this paper, we will consider the fractional-order neural networks with the form

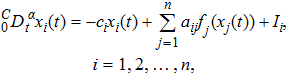(21)
where α is the fractional order, n is the number of units in the neural network, represents the state of the i-th unit at time t, is the constat connection weight of the j-th neuron on the i-th neuron, is a nonlinear function, corresponds to the rate with which the i-th neuron will reset its potential to the resting state when disconnected from the network, and corresponds to the external input.

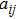
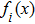
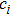
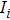
Let us denote , , , , then system (21) can be rearranged to the following compact form:

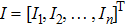
(22)

To guarantee the existence and uniqueness of the solutions of the fractional-order neural network (22) (see Refs. [9] and [52]), we assume that the functions f are Lipschitz-continuous, i.e., for all ,

(23)
where l is the Lipschitz constant.

The slave system is given by

(24)
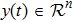
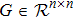
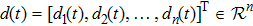
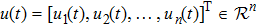
where is the state vector of the slave system, is a positive definite control gain matrix, is an unknown external disturbance, and is the control input.

The objective of our work is to design a robust controller such that the slave system (24) synchronizes the master system (22). To proceed, the following assumption is needed.

3.2. Controller design and stability analysis

In this subsection, an adaptive fuzzy synchronization controller will be designed. Define the synchronization error as . From Eqs. (22) and (24), we have

(25)
where is a fully unknown nonlinear function.

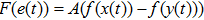
As in Refs. [36] and [44]–[48], we can assume that the fuzzy systems do not violate the universal approximator property. Thus it is rational to give the following assumption.

4. Simulation studies

In this section, a simulation example will be given to show the effectiveness of the proposed synchronization method.

Let , , for i = 1, 2, 3, . With the above system parameters, and let the initial condition be , the master fractional-order neural network (22) has a chaotic attractor, which is presented in Fig. 2.

Fig. 2. (color online) Chaotic behavior of system (21) in (a) , (b) plane, (c) plane and (d) plane.

The initial condition for the slave fractional-order neural networks is chosen as , and the external disturbance is defined as . The control design parameters are given as , , , , , , and . The initial conditions for and are chosen as . To avoid the chattering phenomenon produced by the sign function in Eq. (36), the discontinuous function is replaced by .

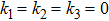
We define 7 Gaussian membership functions distributed on interval [−4, 4] for each input . The synchronization errors may be very small after a period of time, so the memberships should have good performance nearby the origin. In this paper, the parameters of the proposed membership functions are listed in Table 1 (the membership functions have the form ). It is easy to know that there are 7 × 7 × 7 = 343 fuzzy rules used. The initial conditions for are defined as .

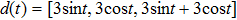
Table 1.

Parameters of the membership functions.

.
Fig. 3. (color online) Membership functions.

The simulation results are presented in Figs. 4–7. The time responses of the synchronization errors are included in Fig. 4. It is shown that the synchronization errors converge to a very small region of the origin after a short period of time although the controller design matrix K in Eq. (36) is chosen as 0. The varieties of the control inputs are depicted in Fig. 5. The norms of the fuzzy system parameters and the estimations of the unknown system parameters are presented in Figs. 5 and 7, respectively. It is worth mentioning that all design parameters are chosen to be small in the simulation, so the control inputs and the time responses of the parameters to be updated online vary in a very stable way. That is to say, good synchronization performance has been achieved based on the proposed control method.

Fig. 4. (color online) Synchronization errors.
Fig. 5. (color online) Control inputs.
Fig. 6. (color online) Fuzzy system parameters.
Fig. 7. (color online) Estimations of the unknown system parameters.

In the rest of this section, we will give some simulation results to show the differences between our control method and that in Ref. [11]. Our design parameters are chosen as above. In Ref. [11], the same system model is used in the simulation, and their design parameters are also chosen as those in Ref. [11] except that the initial values and the external disturbances are changed as above.

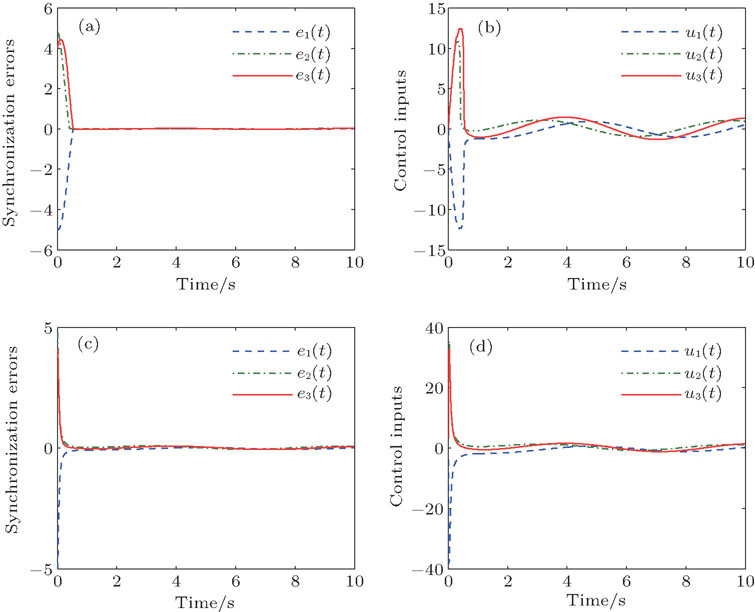It can be concluded from Fig. 8 that the two methods have similar synchronization performance, but in our method, the synchronization will converge to the origin with smaller fluctuation. It should be noted that the comparison results are hard to be concluded because the design parameters in the two controllers are very different. To show the robustness of the two methods, we will increase the disturbances. Let , the simulation results are presented in Fig. 9, from which we can conclude that our method has better robustness compared with the synchronization method in Ref. [11].

Fig. 8. (color online) Simulation results. (a) Synchronization errors and (b) control inputs of our method, (c) synchronization errors and (d) control inputs of Ref. [11].
Fig. 9. (color online) Simulation results with large disturbance. Synchronization errors of (a) our method and (b) Ref. [11].
5. Conclusion

Synchronization of two identical fractional-order neural networks by using an adaptive fuzzy control approach is discussed in this paper. We use the fuzzy logic systems to handle the case that the model of the system is fully unknown. Based on the fractional Lyapunov stability criterion, an adaptive fuzzy controller is given to guarantee that the synchronization errors converge to an arbitrary small region of the origin. It is shown that fractional-order adaptations can be designed to cancel the fuzzy approximation errors and the estimation errors of unknown parameters. By using the results of this paper, some control methods which are proposed for integer-order nonlinear systems may be extended to control fractional-order nonlinear systems. Working towards the simplicity of the controller design and giving simpler stability analysis methods for fractional-order nonlinear systems are our further investigation directions.

Reference
[1] Podlubny I 1998 Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications Academic press
[2] Wu R Lu Y Chen L 2015 Neurocomputing 149 700
[3] Shen J Lam J 2014 Automatica 50 547
[4] Aguila-Camacho N Duarte-Mermoud M A Gallegos J A 2014 Communications in Nonlinear Science and Numerical Simulation 19 2951
[5] Chen L Wu R He Y Yin L 2015 Applied Mathematics and Computation 257 274
[6] Duarte-Mermoud M A Aguila-Camacho N Gallegos J A Castro-Linares R 2015 Communications in Nonlinear Science and Numerical Simulation 22 650
[7] Liu H Li S G Sun Y G Wang H X 2015 Chinese Physics B 24 090505
[8] Liu H Li S G Cao J Alsaedi A Alsaadi F E 2017 Neurocomputing 219 422
[9] Liu H Li S G Sun Y G Wang H X 2015 Acta Phys. Sin. 64 070503 in Chinese
[10] Diethelm K 2010 The analysis of fractional differential equations: An application-oriented exposition using differential operators of Caputo type Springer
[11] Liu H Li S G Wang H X Huo Y Luo J H 2015 Entropy 17 7185
[12] Yu J Hu C Jiang H 2012 Neural Networks 35 82
[13] Chen J Zeng Z Jiang P 2014 Neural Networks 51 1
[14] Bao H B Cao J D 2015 Neural Networks 63 1
[15] Wang F Yang Y Hu M 2015 Neurocomputing 154 239
[16] Chen L Wu R Cao J Liu J B 2015 Neural Networks 71 37
[17] Ding Z Shen Y Wang L 2016 Neural Networks 73 77
[18] Velmurugan G Rakkiyappan R Cao J 2016 Neural Networks 73 36
[19] Huang X Zhao Z Wang Z Li Y 2012 Neurocomputing 94 13
[20] Song C Cao J 2014 Neurocomputing 142 494
[21] Aghababa M P 2012 Nonlinear Dynamics 69 247
[22] Rakkiyappan R Cao J Velmurugan G 2015 IEEE Transactions on Neural Networks and Learning Systems 26 84
[23] Wang H Yu Y Wen G Zhang S Yu J 2015 Neurocomputing 154 15
[24] Xiao M Zheng W X Jiang G Cao J 2015 IEEE Transactions on Neural Networks and Learning Systems 26 3201
[25] Bao H Park J H Cao J 2015 Nonlinear Dynamics 82 1343
[26] Wu A Zeng Z 2016 IEEE Transactions on Neural Networks and Learning Systems
[27] Ding Z Shen Y 2016 Neural Networks 76 97
[28] Yu W Chen G Cao M 2010 Automatica 46 1089
[29] Yu W Zheng W X Chen G Ren W Cao J 2011 Automatica 47 1496
[30] Wen G Duan Z Yu W Chen G 2012 International Journal of Robust and Nonlinear Control 22 170
[31] Yu W Wen G Yu X Wu Z Lü J 2014 Journal of Control and Decision 1 102
[32] Wen G Yu W Wang J Xu D Cao J 2015 Neurocomputing 149 1387
[33] Wen G Yu W Hu G Cao J Yu X 2015 IEEE Transactions on Neural Networks and Learning Systems 26 3239
[34] Pan Y Yu H 2016 IEEE Transactions on Automatic Control 61 2603
[35] Tong S C He X L Zhang H G 2009 IEEE Transactions on Fuzzy Systems 17 1059
[36] Boulkroune A M’Saad M 2011 Expert Systems with Applications 38 14744
[37] Pan Y Er M J Huang D Wang Q 2011 IEEE Transactions on Fuzzy Systems 19 807
[38] Li Y Tong S Li T 2014 Fuzzy Sets and Systems 248 138
[39] Wu T S Karkoub M Chen H S Yu W S Her M G 2015 Information Sciences 290 86
[40] Li Y Tong S 2015 Information Sciences 292 125
[41] Pan Y Zhou Y Sun T Er M J 2013 Neurocomputing 99 15
[42] Boulkroune A Bouzeriba A Hamel S Bouden T 2014 Nonlinear Dynamics 78 433
[43] Pan Y Yu H Sun T 2015 IEEE Transactions on Cybernetics 45 574
[44] Wang L X 1994 Adaptive fuzzy systems and control: design and stability analysis Prentice-Hall Inc
[45] Boulkroune A Tadjine M M’Saad M Farza M 2010 Fuzzy Sets and Systems 161 797
[46] Tong S Li Y 2013 IEEE Transactions on Fuzzy Systems 21 134
[47] Tong S Li Y 2012 IEEE Transactions on Fuzzy Systems 20 168
[48] Pan Y Er M J 2013 IEEE Transactions on Fuzzy Systems 21 1123
[49] Liu H Yu H J Xiang W 2012 Chinese Physics B 21 120505
[50] Li Y Chen Y Podlubny I 2009 Automatica 45 1965
[51] Chang W J Hsu F L 2016 Information Sciences 327 258
[52] Yu J Hu C Jiang H Fan X 2014 Neural Networks 49 87
[53] Roohi M Aghababa M P Haghighi A R 2015 Complexity 21 211