† Corresponding author. E-mail:
The graphene-based double-barrier waveguides induced by electric field have been investigated. The guided modes can only exist in the case of Klein tunneling, and the fundamental mode is absent. The guided modes in the single-barrier waveguide split into symmetric and antisymmetric modes with different incident angles in the double-barrier waveguide. The phase difference between electron states and hole states is also discussed. The phase difference for the two splitting modes is close to each other and increases with the order of guided modes. These phenomena can be helpful for the potential applications in graphene-based optoelectronic devices.
In recent years, more and more research on graphene has been done experimentally and theoretically[1–6] due to its remarkable properties and potential applications.[7–11] Graphene is a single two-dimensional layer of carbon atoms bound in a hexagonal lattice structure, and the quasi particle exactions around the Dirac point obey a linear Dirac-like energy dispersion law, which can be described by a two-dimensional Dirac equation.[8] It exhibits many unique properties.[12–21]
As we all know, quasiparticles in graphene exhibit the linear dispersion relation, which is similar to that of light or photons. Thus it is possible to make an analogy between the propagation of electron waves in a graphene waveguide and electromagnetic waves in dielectric optical waveguides. Electrons in graphene near the Dirac point exhibit some optical-like phenomenon, such as reflection, refraction, and transmission. Moreover, the electrons in graphene have very long mean free paths and seem to be almost insensitive to disorder and electron–electron interactions.[7] Hence, quantum well or barrier in graphene can act as a slab waveguide for electrons wave.[22–28]
It is necessary to compare the difference between an optical waveguide and a graphene waveguide. First, the guided modes in an optical waveguide depend on the configuration of the waveguide and the material properties of the guiding film, the cover, and the substrate. For a graphene waveguide, the layers are characterized by potential energies, which can be modulated by the external electric field without changing the configuration of the waveguide. Secondly, in the graphene waveguide the guided modes are generated due to the propagation of ballistic electrons governed by the Dirac-like equation, while in the dielectric optical waveguide the guided modes are generated due to the propagation of electromagnetic waves satisfying the Helmholtz equation. Many achievements about graphene waveguides have been reported.[24–34] The waveguide induced by a δ-function-like magnetic field exhibits a step-like increase in conductance with increasing fermion energy.[23] The graphene-based waveguide with electrostatic potential modulation and magnetic modulation by ferromagnetic stripes has been investigated.[24–28,35] All of these results show that the characteristics of the guided modes differ due to the different modulation method and different waveguide structures.
The research about graphene-based waveguides mainly focuses on the quantum well structures,[24–27,35] while only a small part of potential barrier structures have been studied.[28,37–39] The graphene waveguide with a single barrier structure has been studied in detail.[28] In the graphene-based double-barrier structures, the giant Goos-Hänchen shift, resonant tunneling, and shot noise have been reported,[37–39] which demonstrate some different properties compared with that in the single barrier structure. The graphene double-barrier structure is an important field, since practical optoelectronic devices are not made of simple structures such as a single quantum barrier or a single quantum well while it may consist of double barriers or double wells. Moreover, the graphene waveguide with a double-barrier structure possesses more extensive physical phenomena than those in the single-barrier structure.
Here we will investigate the guided modes in a graphene-based double-barrier waveguide. The results show that guided modes in double-barrier waveguides will split. The splitting of guided modes is very sensitive to well widths and barrier heights. When the well width, which is the distance interval between two barriers, tends to be large enough, impact between the two barriers will be ignored, and thus the double-barrier waveguides will degenerate into two single barrier waveguides. The phase difference between electron states and hole states has also been discussed and the relationship between the phase difference and the order of guided modes is also illustrated.
In this work, we consider the symmetric double-barrier waveguides induced by monolayer graphene, as shown in Fig.
 | (1) |
In Fig.
The low energy band structure for a single valley (K lattice point) in graphene can be described by the 2D Dirac-like Hamiltonian
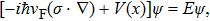 | (2) |





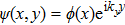
 | (3a) |
 | (3b) |
 | (4a) |
 | (4b) |
Here, we define 

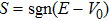
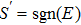







 | (5) |



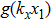






The guided modes in the double-barrier waveguides can only be supported for 


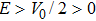
The existence of the guided modes is demonstrated in Fig. 

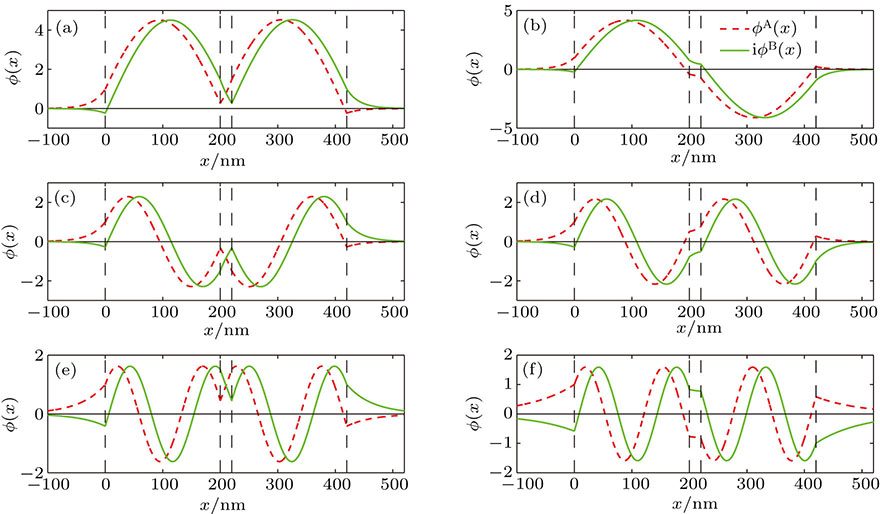
The wave function corresponding to the intersections is represented in Fig.
We find that the modes are from first-order to sixth-order, and the fundamental mode does not exist. Although the order of new modes generated by splitting in the double-barrier waveguides are obviously different from each other, the angle of incidence and energy of x-direction are close to each other for the two splitting modes, such as the first-order and second-order modes. However, the difference of the angle of incidence and energy of x-direction between the two splitting modes increases with the increasing order of the modes, which is shown in Fig.
As reported in the previous papers,[24,25,28,36] the fundamental mode can only exist in the case of classical motion and cannot exist in the Klein tunneling case in the graphene-based waveguide. The graphene double-barrier waveguides support modes only in the case of Klein tunneling, and the fundamental mode is absent. The wave function 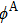








In Fig.
 | Fig. 4. (color online) The dependence of (a) x-direction energy 
|
In order to understand the confinement of the electron wave in the double-barrier waveguides, we calculate the probability current density by the definition in the Dirac equation 


In conclusion, we study the guided modes in the double-barrier waveguides based on graphene. The graphene quantum double barrier can act as an electron waveguide when the incidence angle is larger than the total internal reflection critical angle. The dispersion equation, guided modes chart, wave function, phase difference, and the probability current densities are discussed in detail. It is found that electronic waves can only propagate in the graphene-based double-barrier waveguides in the case of Klein tunneling (
In the double-barrier waveguide, modes splitting take place. Due to a considerable overlap of wave functions in the two barriers, the single-quantum-barrier modes split into symmetric and antisymmetric modes with different incident angles and x-direction energy. Therefore, the double-barrier waveguides can support more guided modes than single barrier waveguides do under the same circumstances. Although the incident angle and the x-direction energy in double-barrier waveguides are different from that in single barrier waveguides, but the difference is very small and can be modulated by incident energy and the electrostatic gates. It gives us a way to fine-tune some of the parameters of the guided modes in the double-barrier waveguides. Furthermore, the double-barrier waveguides have a much wider range of applications than single waveguides and have potential applications in directional couplers and the core component in future electron guided-wave integrated circuits. The split interval of x-direction energy of the doublets becomes larger and larger, and the phase difference between electrons for 

In the graphene-based double-barrier waveguides, the interference and coupling effect may happen, which deserves our further investigation. The graphene-based quantum double-barrier waveguides are potentially useful in electron guided-wave integrated circuits which could perform optical-like processing. We hope these performances of graphene-based double-barrier waveguides can be helpful in designing and motivating the application of graphene-based devices in the future.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] |