The energy transmission of the long microwave pulse for the frequency of 2.45 GHz and 5.8 GHz is studied by using the electron fluid model, where the rate coefficients are deduced from the Boltzmann equation solver named BOLSIG+. The breakdown thresholds for different air pressures and incident pulse parameters are predicted, which show good agreement with the experimental data. Below the breakdown threshold, the transmitted pulse energy is proportional to the square of the incident electric field amplitude. When the incident electric field amplitude higher than the breakdown threshold increases, the transmitted pulse energy decreases monotonously at a high air pressure, while at a low air pressure it first decreases and then increases. We also compare the pulse energy transmission for the frequency of 2.45 GHz with the case of 5.8 GHz.
A solar power satellite is a renewable energy system that converts the sun's energy into electricity in space and transmits it to earth using the microwave pulse.[1,2] One of the essential concerns about the energy transmission from space to earth is the possible air breakdown caused by the high–power microwave pulse. The plasma produced in the air breakdown hinders strongly the microwave pulse energy transmission, since it absorbs and reflects the microwave pulse.[3–6] Consequently, it is very important to study and understand the effect of the air breakdown on the pulse energy transmission.
The microwave pulse breakdown in air has been intensively studied using the experimental methods and theoretical models.[7–10] Cook et al. carried out the breakdown experiments, and observed the wave scattering and diffraction caused by the breakdown plasma.[7] Yang et al. measured the breakdown threshold of the short-pulse microwave at moderate and high pressures.[8] The improved electron energy distribution function was introduced into the global model by Nam et al., and the obtained breakdown formation time is very well matched with the particle-in-cell Monte Carlo collision simulations.[9] Boeuf et al. used the electron fluid model with the effective electron diffusion coefficient to describe the interaction between the microwave and the self-organization breakdown plasma, and predicted the plasma front propagation velocity that agrees very well with the experimental results.[10] Unfortunately, the dependence of the pulse energy transmission on the amplitude, the frequency, and the width of the incident pulse at different air pressures is still unclear.
In this paper, the electron fluid model with a great advantage in speed is used to describe the microwave pulse breakdown in air. The rate coefficients from the Boltzmann equation solver BOLSIG+[11] are introduced into this model. In order to validate the electron fluid model, the breakdown prediction is compared with the experimental data. We consider the dependence of the microwave pulse energy transmission on the electric field amplitude at the high and low pressures. We focus mainly on the cases of the long microwave pulse whose frequency is 2.45 GHz and 5.8 GHz, respectively, since the two frequencies are suitable for the solar power satellite.[1,2]
2. Model
The interaction between the high-power microwave pulse and the plasma produced in the air breakdown is described using the electron fluid model.[12] When assuming that the incident plane wave propagates toward the positive z axis whose electric field is directed in x axis, the basic equations of one-dimensional model can be written as follows:
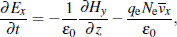(1)
(2)
(3)
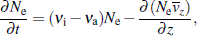(4)
(5)
(6)
(7)
where Ex and Hy are the electric field and magnetic field components of the microwave pulse, Ez is the additional electric field along the z axis generated due to the electrons motion, Ne is the free electron number density, and represent the mean electron velocity components in x–axis and z–axis directions, denotes the mean electron energy, qe} and me denote the charge and mass of electron, ε0 and µ0 are the permittivity and permeability of free space, and Vi, Va, Vm, and Vl are the ionization rate, attachment rate, collision rate, and energy loss rate, respectively.
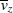
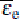
These rate coefficients above are important to describe the interaction between the air molecules and the electrons accelerated by the microwave pulse. The Boltzmann equation solver BOLSIG+[11] is used to deduce these coefficients, whose accuracy have been confirmed by comparing the fluid model simulations with particle–in–cell Monte Carlo collision simulations.[13] It is assumed that the air is composed of 25% oxygen and 75% nitrogen. The relationships among the rate coefficients, the air number density and the mean electron energy are shown in Fig. 1.
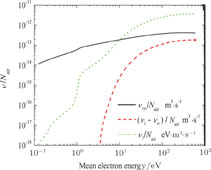Fig. 1. (color online) Ratios of νm, νi–νa, and νl to the air number density Nair as a functionof the mean electron energy.
We solve numerically the electron fluid model by using the finite–difference time–domain method.[14] The simulation domain is 0 < z < 2λ where λ is the wavelength. In iteration calculations, the fine step is adopted, i.e., the space step ∆z = λ/100 and the time step ∆t = ∆z/5c, where c is the speed of light. 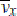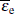It is assumed that the initial electron number density Ne = 1 cm−3, and other components, i.e., Ex, Ez, Ey, , , and e are zero at the initial time. The idealized pulse shape is used, ignoring the finite rise and decay times, which can be written as follows: where Em, f, and tp denote the amplitude, the frequency, and the width of the pulse, respectively.
3. Results and discussion
Taking the case of a low pressure for example, we first give the time evolution of the microwave breakdown, as shown in Fig. 2. The mean electron energy takes a very short time to saturate at around 35 eV [see Fig. 2(b)]. In that case, the ionization rate is high, and the electron number density grows exponentially [see Fig.2(c)]. After the electron number density reaches about 108 times the initial level (1 cm−3), the electric field amplitude begins to decrease sharply [see Fig. 2(a)], and the air breakdown occurs. In other words, the pulse tail energy cannot penetrate the air breakdown environment. This tail–erosion phenomenon also occurs at other pressures.
Fig. 2. (color online) Microwave pulse electric field (a), mean electron energy (b), and electron number density (c) as a function of time at p = 2 Torr (1 Torr = 1.33322 × 102 Pa), f = 2.45 GHz, tp = 12 ns, and Em = 2500 V/cm.
In Fig. 3(a), the breakdown threshold is shown as a function of the air pressure for different microwave frequencies and pulse widths. The breakdown threshold is defined as the pulse electric field amplitude at which the electron density reaches 108 times its initial level during the pulse width tp.[9] This definition also accords with the result of Fig. 2. We see from Fig. 3(a) that the breakdown threshold has the minimum value at about 2 Torr, which agrees very well with the experimental data.[15] When the the pressure decreases, the mean electron energy and corresponding Vi/Nair increase (see Fig. 1), while the air number density Nair decreases. As a result, there is the pressure at which the ionization rate is highest and the breakdown threshold is lowest. Note that the pressure at which the breakdown threshold is lowest depends on the microwave frequency.[16] The average electric field power for accelerating electrons, which has been successfully applied to the case of the frequency range from a few GHz to hundreds of GHz, can be written as[9]
At low pressures, the value of 2πf is near or larger than vm, and PEav then decreases with the microwave frequency increasing. This leads to the fact that, at a higher microwave frequency, the higher electric field is required to achieve the power at which the electron density reaches 108 times its initial level during the pulse width. Therefore, the breakdown threshold of 5.8-GHz 1000-ns microwave pulse is higher than that of 2.45-GHz 1000-ns microwave pulse at low pressures. At high pressures, the dependence of the breakdown threshold on the microwave frequency is very weak, since 2πf ≪vm. Figure 3(a) also shows that the breakdown threshold of the 2.45-GHz 500-ns microwave pulse is approximately equal to that of the 2.45-GHz 1000-ns microwave pulse at high pressures, while at low pressures the former is higher.
Fig. 3. (color online) (a) Breakdown threshold as a function of air pressure. (b) Effective electric field normalized to the air pressure Eeff/p versus ptp.
In Fig. 3(b), the effective electric field
(10)
The collision rate is frequently approximated as Vm = 5.3 × 109p,[10] since it depends weakly on the mean electron energy (see Fig. 1). Using this approximation and Eq. (10), we can deduce the relation among Eb(V/cm), tp(s), and f(GHz) as follows:
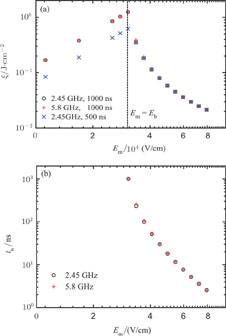
To estimate the pulse energy transmission, it is assumed that the plasma fully absorbs or reflects the pulse tail once the air breakdown occurs. This assumption also agrees very well with the results of Fig. 2. The transmitted pulse energy fluence, ξ, in J/cm2, can then be approximated as
(12)
where tb is the breakdown formation time defined as the time in which the electron number density reaches 108 times the initial level.[9] It is clear that the pulse width tp is equal to the breakdown formation time tb at Em = Eb. Next, we consider the dependence of the pulse energy transmission on the amplitude, frequency, and width of the incident pulse at the high and low pressures, as shown in Figs. 4 and 5.
Fig. 4. (color online) (a) Transmitted pulse energy fluence as a function of electron field amplitude for p = 760 Torr and different frequencies and pulse widths. (b) Breakdown formation time as a function of electron field amplitude for p = 760 Torr and different frequencies.
Fig. 5. (color online) (a) Transmitted pulse energy fluence as a function of electron field amplitude for p = 2 Torr and different frequencies and pulse widths. (b) Breakdown formation time as a function of electron field amplitude for p = 2 Torr and different frequencies.
At p = 760 Torr and Em ≤ Eb, the transmitted pulse energy fluence ξ ∝ E2m [see Eq. (12)], and linearly increases with Em in double logarithmic coordinates, as shown in Fig. 4(a). Nevertheless, at Em > Eb, ξ ∝ E2mtb.With Em increasing, tb decreases sharply [see Fig. 4(b)], and therefore ξ decreases. This suggests that the critical ξ for Em = Eb is maximum. The ξ of 5.8-GHz 1000-ns microwave pulse is approximately equal to that of 2.45-GHz 1000-ns microwave pulse, since the air breakdown depends weakly on the microwave frequency at high pressures. It can also be found from Fig. 4(a) that the longer the pulse width, the higher the critical or maximum transmitted energy.
Figure 5(a) shows that at p = 2 Torr and Em≤Eb, the variation of ξ with Em shows the same trend as the case of p=760 Torr. However, at Em>Eb, ξ first decreases and then increases when Em increases. This can be attributed to the fact that, with Em increasing, the mean electron energy increases from a few eV to several hundred eV, and then tb inverse proportion to the value of vi-va[17] first decreases and then shows little change [see Fig. 1 and Fig. 5(b)]. With the microwave frequency increasing, the average electric field power shown in Eq. (9) decreases, and tb then increases [see Fig. 5(b)]. As a result, the ξ of the 5.8-GHz 1000-ns microwave pulse is higher than that of the 2.45-GHz 1000-ns microwave pulse at E>Eb. The critical ξ for Em = Eb increases when the microwave frequency or the pulse width increases. Unlike the cases of high pressures, the critical ξ may not be maximum.
4. Conclusions
In this paper, we have investigated the effect of the air breakdown on the energy transmission of the long microwave pulse at the frequency of 2.45 GHz and 5.8 GHz by using the electron fluid model. In this model, the rate coefficients such as the ionization rate are deduced from the Boltzmann equation solver BOLSIG+. We predict the breakdown threshold, and analyze its dependence on the pressure and incident pulse parameters. The breakdown prediction also shows good agreement with the experimental data. When the pulse electric field amplitude is lower than the breakdown threshold, the transmitted pulse energy linearly increases with the square of the electric field amplitude. At a high pressure, the transmitted pulse energy decreases monotonously when the electric field amplitude higher than the breakdown threshold increases, and the critical transmitted energy for the electric field amplitude equal to the breakdown threshold is maximum. At a low pressure, the transmitted pulse energy first decreases and then increases when the electric field amplitude higher than the breakdown threshold increases. At a high pressure the transmitted pulse energy for the frequency of 5.8 GHz is approximately equal to that for 2.45 GHz, while at a low pressure and above the breakdown threshold, the former is larger. We also compare the transmitted pulse energies for two different pulse widths.
